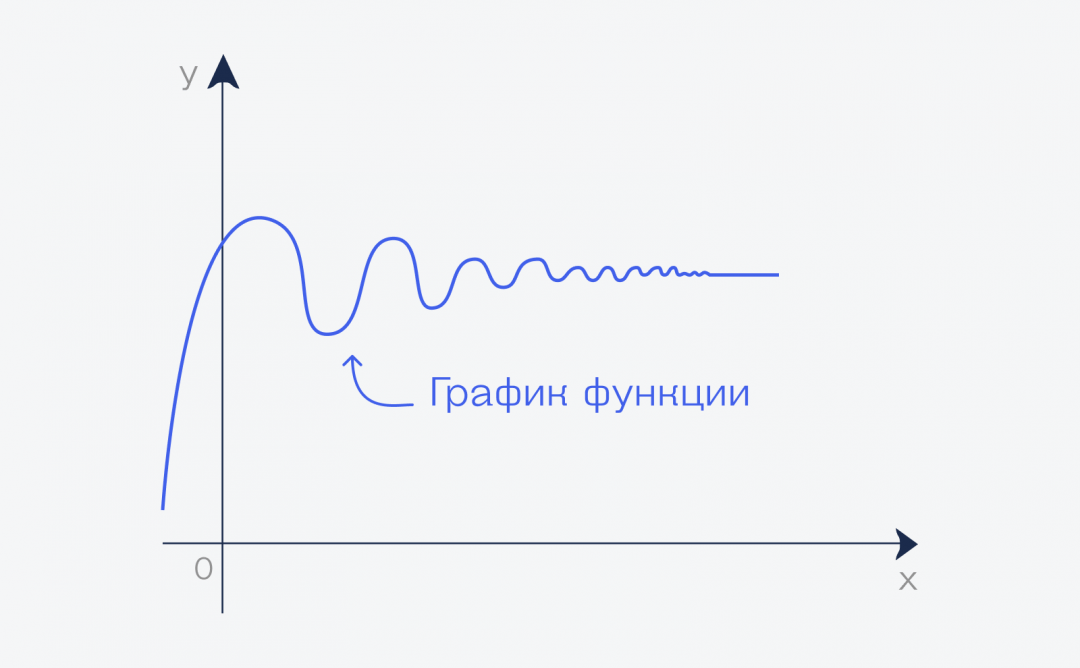
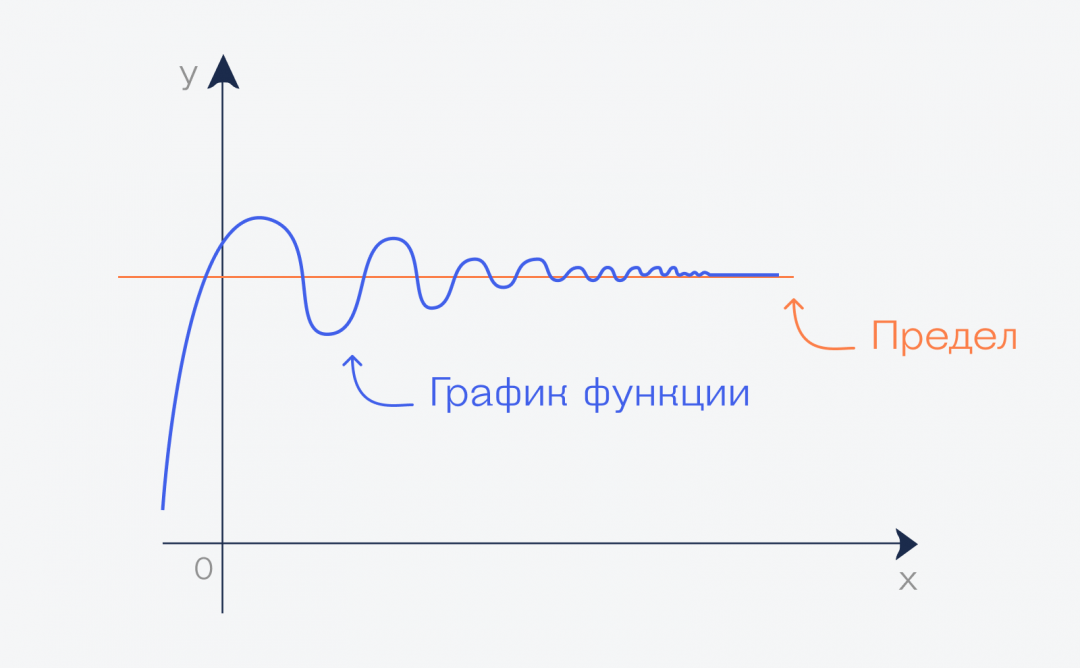
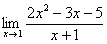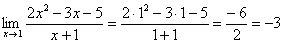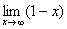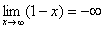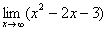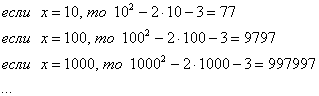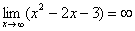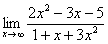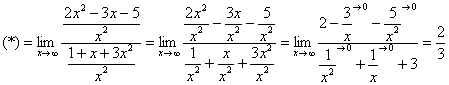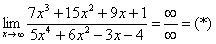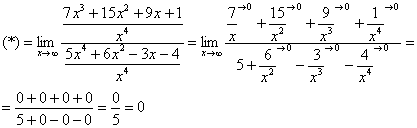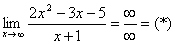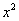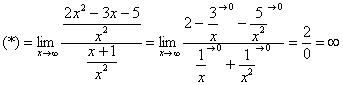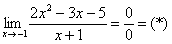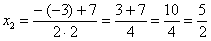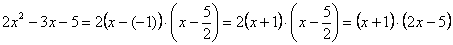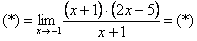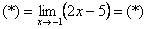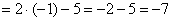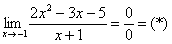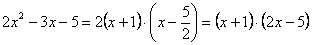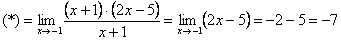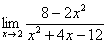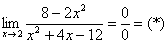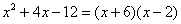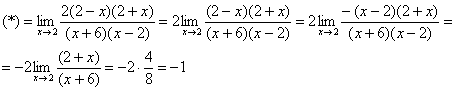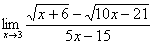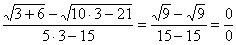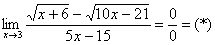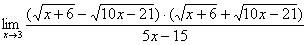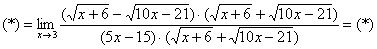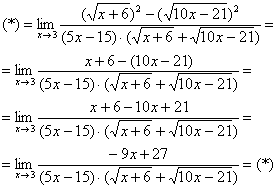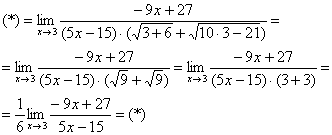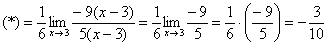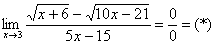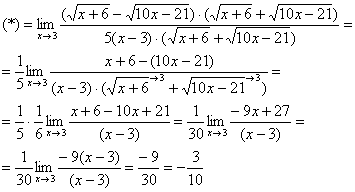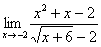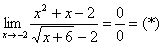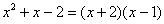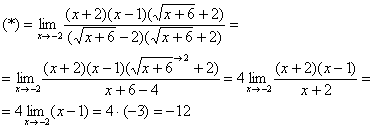Предел функции для чего нужен

Пределы

Пределы — одни из самых трудных сущностей в математике для понимания. Сложно объяснить просто, что такое предел, поэтому чаще всего этого никто и не делает.

И тем более, мало к то из преподавателей может привести пример из жизни, когда пределы все-таки могут пригодиться. Но мы попытаемся объяснить так, чтобы было и понятно и несложно и по сути. Как обычно «на пальцах».

Что такое пределы простыми словами

Наверное самое наглядное, что можно вспомнить из истории, это знаменитый парадокс Зенона «Ахиллес и черепаха». Зенон был философом, а не математиком, поэтому мог вполне свободно упражняться в остроумии не заботясь о доказательствах.

Ахиллес и черепаха бегут на перегонки. Черепаха начинает первой, человек догоняет. Ахиллес бежит быстрее, но когда он пробегает 100 шагов, черепаха все рано проползает один. Еще 100 шагов и еще один. Таким образом Ахиллес приближается к черепахе но и она чуть-чуть отдаляется от него. Зенон делает вывод, что Ахиллес будет бесконечно к ней приближаться, но никогда не догонит черепаху!

В этой истории важно не то, что на самом деле она не реальна, а ее «математический смысл». Человек приближается к черепахе но никогда ее не настигает. То есть некий предел (черепаха) к которому стремится Ахиллес.

Говоря простым языком, предел это такое значение, которое нельзя достичь, но можно бесконечно близко к нему приблизится.

То есть, в пределе определенного промежутка времени Ахиллес действительно не догонит черепаху (времени не хватит), но приблизится к ней на бесконечно малое расстояние.

Что такое пределы в математике

Стоит сразу сказать, что определение пределов больше чем одно, потому, что они бывают разные. Есть придел последовательности, а есть предел функции.

Давайте разделим число 10 пополам:

10/2=5, и еще раз, 5/2=2,5 и еще…

Это последовательность n/2: 10…2,5…1,25…

Если делать это 20 раз получится вот такое значение: 0,000019

А если сделать 100 раз, то вот такое: 0,000000000000000000000000000016

Если делить пополам бесконечно, результат будет уменьшатся, в реальной жизни, это будет уже фактически ноль, но в математике, все еще не ноль… Предел этой последовательности будет стремиться к нолю.

Если взять другу последовательность, например n+1. 2…3…4…5… и снова устремимся в бесконечность. Предел этого множества тоже будет стремится к бесконечности.

Еще один пример

Бросаем монетку. Может выпасть «орел», а может и «решка». Теория вероятности утверждает, что шансы всегда 50/50, то есть вероятность «орла» — 1/2=0,5.

Каждый раз, значение реальной вероятности, приближается к расчетным 0,5. Чтобы получить вероятность ровно 0,5 нужно подбросить монетку бесконечное количество раз.

То есть, при условии, что количество бросков стремится к бесконечности предел предел будет равен 0,5.

Это именно та бесконечность из матанализа о которой было сказано в статьях об интегралах и делении на ноль. Это не какое-то определенное число — это понятие.

Предел последовательности

Предел последовательности — это пространство которое содержит все все элементы последовательности начиная с какого-то значения.

А простыми словами, предел последовательности, простыми словами, это такая «область» куда попадают все значения после определенного порога (в нашем случае – А). На изображении ниже она условно показана синей полоской.

ε — это произвольное положительное число.

Можно заметить, что при продолжении вверх последовательности ее значения все равно будут оставаться в пределах «синей полосы».

Можно сказать и так:

Предел числовой последовательности, это число (s на графике) в окрестности которого попадает бесконечно много значений. При этом вне предела, количество значений явно конечно.

Чтобы было еще понятнее: предел последовательности это значение (точка А) выше которого все будет попадать в область не больше s+ε и s-ε. Бесконечное количество таких значений будет «лежать» внутри синей полоски.

Математическим языком можно записать так: s-ε Предел функции простыми словами объяснить также просто. Предел в какой-то произвольной точке — это величина к которой значение функции приближается. Например, f(x)=2x, а х→0 (икс стремится к нулю).

В этом случае предел функции будет равен lim 2x=0. Или в случае если х→2 то предел равен lim 2x=4. Пока все просто. Вот только зачем вычислять пределы, если можно просто выбросить «lim» и расчеты останутся те ми же?….

Зачем нужны пределы

Пределы как раз и нужны тогда, когда мы имеем дело с бесконечностью. Например, бесконечно большими или бесконечно малыми значениями.

Непонятно, что такое «бесконечно большое» или «бесконечно долго», это не какое-то определенное число. С бесконечно малыми значениями та же ситуация, это не «ноль» но как-то очень близко к нему. Тут и выручают пределы.

В точке х=2 — пусто. Потому, что получается 0/0, то есть неопределенность. Но стоит вместо 2 подставить 1,9999999999(9) или 2,000000001(1). Значения бесконечно близкие к 2, но не «два», как график превратится в прямую.

В этом случае речь идет о пределе функции при «икс» стремящемуся к двум, функция стремится к 4.

Такой своеобразный «трюк» в расчетах с заменой знака равенства на стрелочку.

Нет, не совсем. Когда речь идет о пределах, имеется в виду процесс, не важно функция это или множество, но предел описывает процесс в динамике. Тогда как знак «равно» означает статическое состояние.

x=1 и x→1, это совсем не одно и то же.

Примеры из жизни

Зачем все это нужно где применяется пределы в реальных расчетах?

Простое объяснение пределов невозможно, если не привести наглядный пример. Но только где его взять? Существует ли какой-то физический смысл пределов? Не точный аналог но что-то похожее есть.

Можно провести простой эксперимент, взять, например, спичку. Или что-угодно, чего не жалко. Начинаем пытаться сломать спичку, сначала одно усилие, потом чуть больше и еще больше. В один из моментов спичка треснет пополам.

Поздравляем, вы достигли предела прочности. Можно повторить эксперимент с другими спичками и установить, значение при котором спичка ломается.

Что тут общего с пределами из математики, кроме названия.

Есть множество значений силы до предела прочности и оно ограничено, и множество значений после предела прочности, их неограниченное множество. Ведь спичка уже сломана, любое усилие выше предела прочности будет ломать новую и новую спичку. Точно так же как и с пределом функции или множества.

Все, что лежит за пределом, уже не имеет практического значения — спичка не устоит.

Еще один пример, это «практический потолок» летательного аппарата. Это максимальная высота на которую может «взобраться» самолет, чтобы подняться выше будет уже не хватать подъемной силы. Хотя на есть еще и понятие «динамический потолок» — это высота на которую можно подняться хорошенько разогнавшись.

Но, выскочив на эту высоту, через некоторое время самолет все равно опустится на свой «потолок».

Посмотрите на картинку ниже, это наглядный пример такого явления как резонанс.

Колебание моста из-за резонанса

Мост так раскачивается из-за того, что собственная частота колебания совпадает с той частотой с которой его раскачивает ветер, амплитуда колебаний постоянно возрастает и мост разрушается. В этом случае амплитуда стремится к бесконечности, так как в знаменателе формулы находится выражение w₀-w (собственная частота колебаний минус вынужденная частота), а так как обе w равны, получается то самое деление на ноль, а значит амплитуда → ∞.

Самое понятное объяснений пределов в реальности, с которым может столкнуться каждый — это сложные банковские проценты по кредиту. И если вы не умеете рассчитывать сложны проценты, не берите кредит. Для тех, кто силен в матанализе совет будет не лишним.

Также может понадобится рассчитать предельную стоимость товара, зная зависимость (функцию) цены от объема продаж или предельный объем производства или много еще чего.

Самый наглядный пример, возможно, это предел в маркетинге. Вот зависимость стоимости клика от количества кликов в контекстной рекламе.

И все же, в повседневной жизни обыватель редко встречается с таким понятием как предел функции или последовательности. Поэтому и так сложно понять и принять абстрактные математические формулировки.

Но, если постараться, математика может открыть новые грани реальности, по крайней мере, все это уже не будет казаться таким скучным и непонятным.

Источник

Пределы в математике для чайников: объяснение, теория, примеры решений

Теория пределов – раздел математического анализа. Наряду с системами линейных уравнений и диффурами пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.

В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Понятие предела в математике

Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a, то a – предел этой величины.

Для определенной в некотором интервале функции f(x)=y пределом называется такое число A, к которому стремится функция при х, стремящемся к определенной точке а. Точка а принадлежит интервалу, на котором определена функция.

Звучит громоздко, но записывается очень просто:

Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.

Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:

Кстати, если Вас интересуют базовые операции над матрицами, читайте отдельную статью на эту тему.

В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:

Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.

Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х. Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность. Что делать в таких случаях? Прибегать к хитростям!

Неопределенности в пределах

Неопределенность вида бесконечность/бесконечность

Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?

Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:

Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Еще один вид неопределенностей: 0/0

В таких случаях рекомендуется раскладывать числитель и знаменатель на множители. Но давайте посмотрим на конкретный пример. Нужно вычислить предел:

Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:

Сократим и получим:

Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.

Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:

Правило Лопиталя в пределах

Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?

Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.

Наглядно правило Лопиталя выглядит так:

Важный момент : предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.

А теперь – реальный пример:

Налицо типичная неопределенность 0/0. Возьмем производные от числителя и знаменателя:

Вуаля, неопределенность устранена быстро и элегантно.

Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос «как решать пределы в высшей математике». Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Предел функции: основные понятия и определения

В этой статье мы расскажем, что из себя представляет предел функции. Сначала поясним общие моменты, которые очень важны для понимания сути этого явления.

Понятие предела

Если мы не можем определить ни конечное, ни бесконечное значение, это значит, что такого предела не существует. Примером этого случая может быть предел от синуса на бесконечности.

Что такое предел функции

В этом пункте мы объясним, как найти значение предела функции в точке и на бесконечности. Для этого нам нужно ввести основные определения и вспомнить, что такое числовые последовательности, а также их сходимость и расходимость.

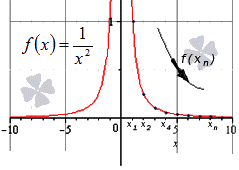
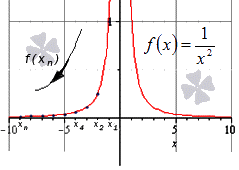
При x → ∞ предел функции f ( x ) является бесконечным, если последовательность значений для любой бесконечно большой последовательности аргументов будет также бесконечно большой (положительной или отрицательной).

Решение

Далее мы запишем то же самое, но для бесконечно большой отрицательной последовательности.

Здесь тоже видно монотонное убывание к нулю, что подтверждает верность данного в условии равенства:

Ответ: Верность данного в условии равенства подтверждена.

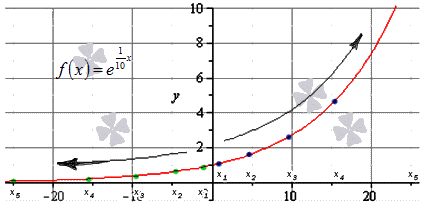
Решение

Мы видим, что данная последовательность бесконечно положительна, значит, f ( x ) = lim x → + ∞ e 1 10 x = + ∞

Наглядно решение задачи показано на иллюстрации. Синими точками отмечена последовательность положительных значений, зелеными ­ – отрицательных.

Перейдем к методу вычисления предела функции в точке. Для этого нам нужно знать, как правильно определить односторонний предел. Это пригодится нам и для того, чтобы найти вертикальные асимптоты графика функции.

Теперь сформулируем, что такое предел функции справа.

Теперь мы разъясним данные определения, записав решение конкретной задачи.

Решение

Значения функции в этой последовательности будут выглядеть так:

Чтобы более глубоко изучить теорию пределов, советуем вам прочесть статью о непрерывности функции в точке и основных видах точек разрыва.

Источник

Что означает предел в математике

Сага о погрешностях при участии слова lim

Кто о чём, а мы продолжаем разбирать сложную математику, чтобы она не была такой сложной.

Что такое предел в математике

Когда математики говорят о пределах, то имеют в виду такую последовательность событий:

Самое простое объяснение функции в математике.

👉 Стремиться — значит стараться приблизиться к какому-то числу, но не достигнуть его.

Если мы говорим, что переменная функции стремится к бесконечности, то это значит, что с каждым новым вычислением мы берём значение переменной больше предыдущего.

1, 2, 3, … 1000000000000003, 1000000000000004 и так до бесконечности

Наоборот тоже работает: если переменная функции стремится к нулю, то это значит, что она постоянно уменьшается:

1, 0.1, 0.01, 0.001, … 0.00000000000000000000000001 и с каждым разом число будет ближе к нулю, но никогда его не достигнет.

Стремление переменной к числу обозначается стрелкой: x→0, а предел — словом lim:

График и предел

Если мы нарисуем график этой функции, то можем увидеть, что начиная с какого-то момента он превратится в почти прямую линию вдоль оси. Почти прямую — потому что прямой он никогда не станет, но стремится к этому, если продолжить рисовать график бесконечно.

Но бесконечный график означает, что у нас переменная функции стремится к бесконечности. А значение этой линии на графике — это и есть предел этой функции при переменной, стремящейся к бесконечности:

Пределы в жизни

Пределы из математики часто используются для решения практических задач, где нужно найти точку, после которой разница в результате будет уже незаметна.

Например, бригада монтажников строит мост, и им нужно понять, какой максимальной длины можно сделать плиту перекрытия. Есть требования, что плита должна выдерживать в середине нагрузку в 50 тонн — она может быть и прочнее, но 50 тонн это минимум. Для решения этой задачи используют предел — он покажет, длиннее какого размера делать плиту нельзя, а всё, что короче, даст необходимую прочность.

Астрономы с помощью пределов изучают законы Вселенной, физики проверяют всё на прочность, и даже в микроэлектронике затухание сигналов тоже зависит от пределов функций.

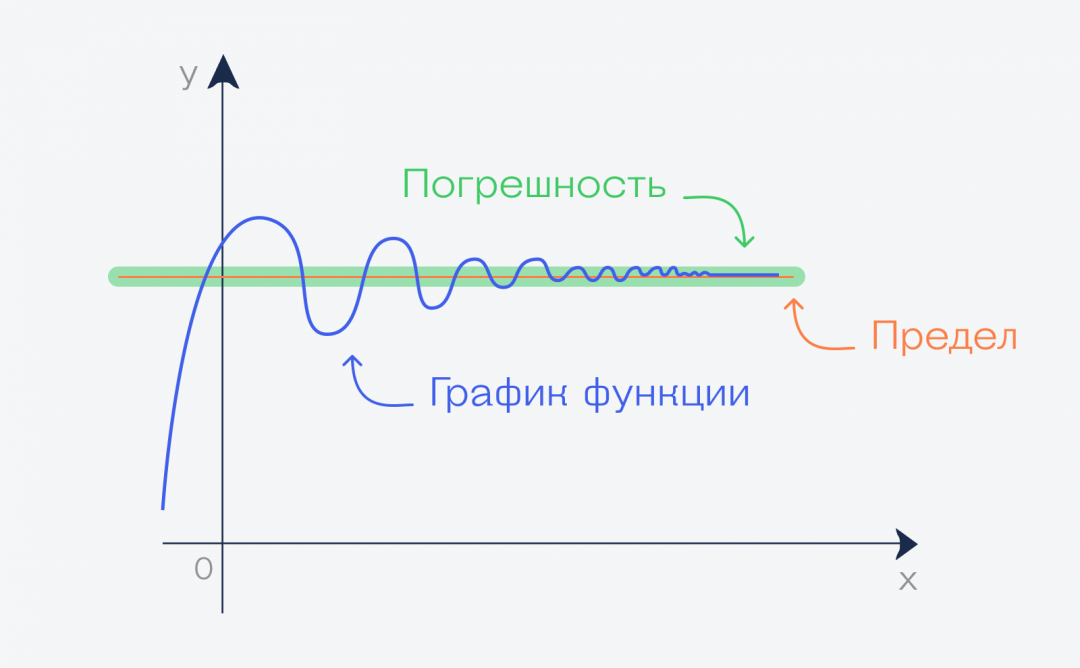
Погрешность в пределах

В математике пределы считаются точно: используются специальные формулы и трюки, которые помогают найти точный ответ. Но в жизни такая точность необязательна: можно взять любое решение, которое нас устроит с приемлемой погрешностью.

Эта погрешность поможет нам считать пределы, не зная точных математических формул подсчёта.

Считаем предел в программировании

Раз у нас есть постоянное действие по уменьшению или увеличению переменной, то логично сделать из этого простой цикл и поручить его машине. Единственное, что нам нужно предусмотреть, — момент, когда цикл должен остановиться, потому что в мире математики lim по умолчанию касается бесконечности (потому что стремиться можно бесконечно).

Так как мы не знаем заранее точного предела функции, но можем контролировать количество повторений, то сделаем такие условия для остановки цикла:

Самый сложный момент в коде — описать то, как переменная функции к чему-то стремится. Если к бесконечности, то всё просто: на каждом шаге прибавляем или умножаем на какое-то число. А если нужно, чтобы переменная стремилась к нулю или другому числу, то можно действовать так: брать начальное число, конечное, складывать их и делить пополам. Так мы будем постоянно приближаться к нужному нам числу, но никогда его не достигнем.

⚠️ Важная оговорка: числа в компьютере — это не числа в абстрактном математическом понимании, а конечный набор данных. Конечный он тем, что на всякое число выделяется какое-то количество «клеток», в которые это число можно записать. Если у нас ограниченное количество «клеток», значит, у нас есть какой-то предел самого большого и самого малого числа.

С точки зрения математики любое число можно бесконечно делить и получать бесконечное число знаков после запятой; а с точки зрения компьютера бесконечное число знаков невозможно, и если делить достаточно долго — мы получим ноль.

Поэтому в работе с пределами важно указывать либо число шагов для определения предела, либо погрешность.

Теперь напишем простой цикл, который нам посчитает lim x→2 (8−2x) / (x²−4x−12):

Если мы посчитаем этот предел как математики, то получим значение −1. Проверим, как с этим справится наш код:

Программа справилась и выдала результат с нужной нам точностью

Источник

Пределы функций. Примеры решений

Теория пределов – это один из разделов математического анализа. Вопрос решения пределов является достаточно обширным, поскольку существуют десятки приемов решений пределов различных видов. Существуют десятки нюансов и хитростей, позволяющих решить тот или иной предел. Тем не менее, мы все-таки попробуем разобраться в основных типах пределов, которые наиболее часто встречаются на практике.

Начнем с самого понятия предела. Но сначала краткая историческая справка. Жил-был в 19 веке француз Огюстен Луи Коши, который дал строгие определения многим понятиям матана и заложил его основы. Надо сказать, этот уважаемый математик снился, снится и будет сниться в кошмарных снах всем студентам физико-математических факультетов, так как доказал огромное количество теорем математического анализа, причём одна теорема убойнее другой. В этой связи мы пока не будем рассматривать определение предела по Коши, а попытаемся сделать две вещи:

1. Понять, что такое предел.
2. Научиться решать основные типы пределов.

Прошу прощения за некоторую ненаучность объяснений, важно чтобы материал был понятен даже чайнику, что, собственно, и является задачей проекта.

Итак, что же такое предел?

А сразу пример, чего бабушку лохматить….

Любой предел состоит из трех частей:

1) Всем известного значка предела .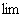
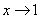
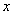
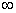
2) Записи под значком предела, в данном случае . Запись читается «икс стремится к единице». Чаще всего – именно , хотя вместо «икса» на практике встречаются и другие переменные. В практических заданиях на месте единицы может находиться совершенно любое число, а также бесконечность ().
3) Функции под знаком предела, в данном случае .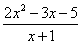

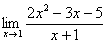
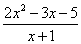
Сама запись читается так: «предел функции при икс стремящемся к единице».

Разберем следующий важный вопрос – а что значит выражение «икс стремится к единице»? И что вообще такое «стремится»?
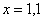
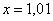
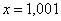
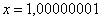
Понятие предела – это понятие, если так можно сказать, динамическое. Построим последовательность: сначала , затем , , …, , ….
То есть выражение «икс стремится к единице» следует понимать так – «икс» последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают.

Как решить вышерассмотренный пример? Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:

Итак, первое правило: Когда дан любой предел, сначала просто пытаемся подставить число в функцию.

Мы рассмотрели простейший предел, но и такие встречаются на практике, причем, не так уж редко!

Пример с бесконечностью:

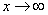
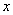
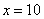
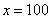
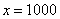
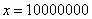
Разбираемся, что такое ? Это тот случай, когда неограниченно возрастает, то есть: сначала , потом , потом , затем и так далее до бесконечности.

А что в это время происходит с функцией ?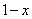
, , , …

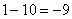
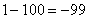
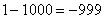
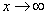
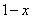
Итак: если , то функция стремится к минус бесконечности:

Грубо говоря, согласно нашему первому правилу, мы вместо «икса» подставляем в функцию 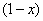бесконечность и получаем ответ.

Еще один пример с бесконечностью:

Опять начинаем увеличивать 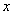до бесконечности и смотрим на поведение функции:

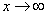
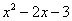
Вывод: при функция неограниченно возрастает:

И еще серия примеров:

Пожалуйста, попытайтесь самостоятельно мысленно проанализировать нижеследующее и запомните простейшие виды пределов:

, , , , , , , , ,
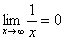
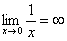
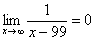
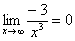
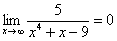
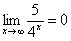
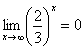
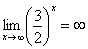
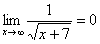
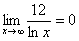
Если где-нибудь есть сомнения, то можете взять в руки калькулятор и немного потренироваться.
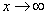
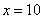
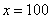
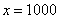
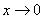
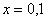
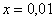
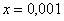
В том случае, если , попробуйте построить последовательность , , . Если , то , , .

! Примечание: строго говоря, такой подход с построением последовательностей из нескольких чисел некорректен, но для понимания простейших примеров вполне подойдет.

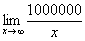
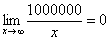
Также обратите внимание на следующую вещь. Даже если дан предел с большим числом вверху, да хоть с миллионом: , то все равно , так как рано или поздно «икс» начнёт принимать такие гигантские значения, что миллион по сравнению с ними будет самым настоящим микробом.

Что нужно запомнить и понять из вышесказанного?

1) Когда дан любой предел, сначала просто пытаемся подставить число в функцию.

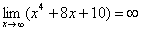
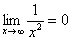
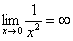
2) Вы должны понимать и сразу решать простейшие пределы, такие как , , и т.д.

Более того, у предела есть очень хороший геометрический смысл. Для лучшего понимания темы рекомендую ознакомиться с методическим материалом Графики и свойства элементарных функций. После прочтения этой статьи вы не только окончательно поймете, что такое предел, но и познакомитесь с интересными случаями, когда предела функции вообще не существует!

На практике, к сожалению, подарков немного. А поэтому переходим к рассмотрению более сложных пределов. Кстати, по этой теме есть интенсивный курс в pdf-формате, который особенно полезен, если у Вас ОЧЕНЬ мало времени на подготовку. Но материалы сайта, разумеется, не хуже:

Пределы с неопределенностью вида 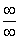и метод их решения

Сейчас мы рассмотрим группу пределов, когда 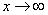, а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены

Вычислить предел

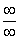
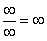
Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида . Можно было бы подумать, что , и ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый прием решения, который мы сейчас и рассмотрим.

Как решать пределы данного типа?

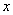
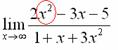
Сначала мы смотрим на числитель и находим в старшей степени:

Старшая степень в числителе равна двум.

Теперь смотрим на знаменатель и тоже находим 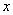в старшей степени:

Старшая степень знаменателя равна двум.

Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.

Итак, метод решения следующий: для того, чтобы раскрыть неопределенность необходимо разделить числитель и знаменатель на в старшей степени.

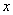
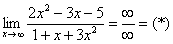
Разделим числитель и знаменатель на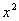

Вот оно как, ответ 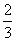, а вовсе не бесконечность.

Что принципиально важно в оформлении решения?

Во-первых, указываем неопределенность, если она есть.

Во-вторых, желательно прервать решение для промежуточных объяснений. Я обычно использую знак 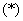, он не несет никакого математического смысла, а обозначает, что решение прервано для промежуточного объяснения.

В-третьих, в пределе желательно помечать, что и куда стремится. Когда работа оформляется от руки, удобнее это сделать так: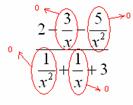

Для пометок лучше использовать простой карандаш.

Конечно, можно ничего этого не делать, но тогда, возможно, преподаватель отметит недочеты в решении либо начнет задавать дополнительные вопросы по заданию. А оно Вам надо?

Найти предел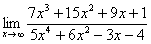
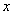
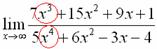
Снова в числителе и знаменателе находим в старшей степени:

Максимальная степень в числителе: 3
Максимальная степень в знаменателе: 4
Выбираем наибольшее значение, в данном случае четверку.
Согласно нашему алгоритму, для раскрытия неопределенности 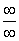делим числитель и знаменатель на .
Полное оформление задания может выглядеть так:

Разделим числитель и знаменатель на

Найти предел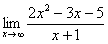
Максимальная степень «икса» в числителе: 2
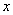
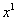
Максимальная степень «икса» в знаменателе: 1 ( можно записать как )
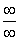
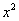
Для раскрытия неопределенности необходимо разделить числитель и знаменатель на . Чистовой вариант решения может выглядеть так:

Разделим числитель и знаменатель на

Под записью 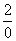подразумевается не деление на ноль (делить на ноль нельзя), а деление на бесконечно малое число.

Таким образом, при раскрытии неопределенности вида 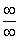у нас может получиться конечное число, ноль или бесконечность.

Пределы с неопределенностью вида 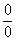и метод их решения

Предвосхищаю вопрос от чайников: «Почему здесь деление на ноль? На ноль же делить нельзя!». Смысл записи 0:0 будет понятен позже, после ознакомления с четвёртым уроком о бесконечно малых функциях. А пока всем начинающим изучать математический анализ предлагаю читать далее.

Следующая группа пределов чем-то похожа на только что рассмотренные пределы: в числителе и знаменателе находятся многочлены, но «икс» стремится уже не к бесконечности, а к конечному числу.

Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида 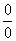, то для ее раскрытия нужно разложить числитель и знаменатель на множители.

Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения. Если данные вещи позабылись, тогда посетите страницу Математические формулы и таблицы и ознакомьтесь с методическим материалом Горячие формулы школьного курса математики. Кстати его лучше всего распечатать, требуется очень часто, да и информация с бумаги усваивается лучше.

Итак, решаем наш предел

Разложим числитель и знаменатель на множители

Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение: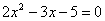

Сначала находим дискриминант: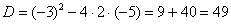

И квадратный корень из него: .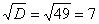

В случае если дискриминант большой, например 361, используем калькулятор, функция извлечения квадратного корня есть на самом простом калькуляторе.

! Если корень не извлекается нацело (получается дробное число с запятой), очень вероятно, что дискриминант вычислен неверно либо в задании опечатка.

Далее находим корни: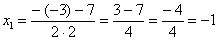

Таким образом:

Всё. Числитель на множители разложен.

Знаменатель. Знаменатель 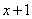уже является простейшим множителем, и упростить его никак нельзя.

Очевидно, что можно сократить на :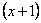

Естественно, в контрольной работе, на зачете, экзамене так подробно решение никогда не расписывают. В чистовом варианте оформление должно выглядеть примерно так:

Разложим числитель на множители.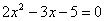

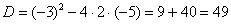
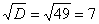
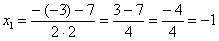
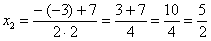
Вычислить предел

Сначала «чистовой» вариант решения

Разложим числитель и знаменатель на множители.

Числитель: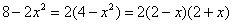
Знаменатель: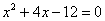



,

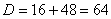
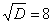
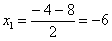
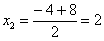
Что важного в данном примере?
Во-первых, Вы должны хорошо понимать, как раскрыт числитель, сначала мы вынесли за скобку 2, а затем использовали формулу разности квадратов. Уж эту-то формулу нужно знать и видеть.

Рекомендация: Если в пределе (практически любого типа) можно вынести число за скобку, то всегда это делаем.
Более того, такие числа целесообразно выносить за значок предела. Зачем? Да просто чтобы они не мешались под ногами. Главное, потом эти числа не потерять по ходу решения.

Обратите внимание, что на заключительном этапе решения я вынес за значок предела двойку, а затем – минус.

Вообще, я заметил, что чаще всего в нахождении пределов данного типа приходится решать два квадратных уравнения, то есть и в числителе и в знаменателе находятся квадратные трехчлены.

Метод умножения числителя и знаменателя на сопряженное выражение

Продолжаем рассматривать неопределенность вида

Следующий тип пределов похож на предыдущий тип. Единственное, помимо многочленов, у нас добавятся корни.

Найти предел

Сначала пробуем подставить 3 в выражение под знаком предела
Еще раз повторяю – это первое, что нужно выполнять для ЛЮБОГО предела. Данное действие обычно проводится мысленно или на черновике.

Получена неопределенность вида 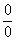, которую нужно устранять.

Как Вы, наверное, заметили, у нас в числителе находится разность корней. А от корней в математике принято, по возможности, избавляться. Зачем? А без них жизнь проще.

Когда в числителе (знаменателе) находится разность корней (или корень минус какое-нибудь число), то для раскрытия неопределенности 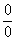используют метод умножения числителя и знаменателя на сопряженное выражение.

Вспоминаем нашу нетленную формулу разности квадратов: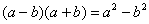
И смотрим на наш предел: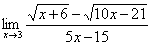
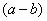
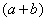
Что можно сказать? у нас в числителе уже есть. Теперь для применения формулы осталось организовать (которое и называется сопряженным выражением).

Умножаем числитель на сопряженное выражение:

Обратите внимание, что под корнями при этой операции мы ничего не трогаем.

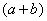
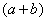
Хорошо, мы организовали, но выражение-то под знаком предела изменилось! А для того, чтобы оно не менялось, нужно его разделить на то же самое, т.е. на :

То есть, мы умножили числитель и знаменатель на сопряженное выражение.
В известной степени, это искусственный прием.

Умножили. Теперь самое время применить вверху формулу :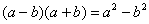

Неопределенность 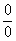не пропала (попробуйте подставить тройку), да и корни тоже не исчезли. Но с суммой корней всё значительно проще, ее можно превратить в постоянное число. Как это сделать? Да просто подставить тройку под корни:

Число, как уже отмечалось ранее, лучше вынести за значок предела.

Теперь осталось разложить числитель и знаменатель на множители и сократить «виновников» неопределённости, ну а предел константы – равен самой константе:

Как должно выглядеть решение данного примера в чистовом варианте?
Примерно так:

Умножим числитель и знаменатель на сопряженное выражение.

Найти предел

Сначала попробуйте решить его самостоятельно.

Окончательное решение примера может выглядеть так:

Разложим числитель на множители: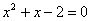

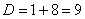
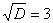
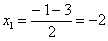
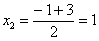
Умножим числитель и знаменатель на сопряженное выражение

Спасибо за внимание.

Помимо рассмотренных типов пределов на практике часто встречаются так называемые Замечательные пределы. После освоения двух базовых уроков, рекомендую изучить статью Методы решения пределов, материалы которой позволят выйти на «твёрдую четвёрку»!

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник