Постройте отрицания следующих высказываний и выясните что истинно данное высказывание или отрицание
Постройте отрицания следующих высказываний и выясните что истинно данное высказывание или отрицание
5.2. Укажите, какие из высказываний предыдущего упражнения истинны, какие ложны, а какие относятся к числу тех, истинность которых трудно или невозможно установить.
[ Ответ ]
5.8. Формализуйте следующий вывод: «Если a и b истинны, то c истинно. Но c ложно: значит, a или b ложны».
[ Ответ ]
5.9. Формализуйте предостережение, которое одна жительница древних Афин сделала своему сыну, собиравшемуся заняться политической деятельностью: “ Если ты будешь говорить правду, то тебя возненавидят люди. Если ты будешь лгать, то тебя возненавидят боги. Но ты должен говорить правду или лгать. Значит, тебя возненавидят люди или возненавидят боги ”.
Формализуйте также ответ сына: “ Если я буду говорить правду, то боги будут любить меня. Если я буду лгать, то люди будут любить меня. Но я должен говорить правду или лгать. Значит, меня будут любить боги или меня будут любить люди ”.
[ Ответ ]
5.10. Пусть a = “ это утро ясное ”, а b = “ это утро теплое ”. Выразите следующие формулы на обычном языке: 
5.12. Из трех данных высказываний a, b, c постройте составное высказывание, которое истинно, когда истинно какое-либо одно из данных высказываний, и только в этом случае.
Ответ: 
5.13. Определите с помощью таблиц истинности, какие из следующих формул являются тождественно истинными или тождественно ложными:
а)  | д)  |
б)  | е)  |
в)  | ж)  |
г)  |
5.18. Найдите функции проводимости следующих переключательных схем:
| а) |  | б) |  |
| в) |  | г) |  |
5.20. Постройте переключательные схемы с заданными функциями проводимости:
5.21. Упростите функции проводимости и постройте переключательные схемы, соответствующие упрощенным функциям:
а)
5.23. Три девочки Роза, Маргарита и Анюта представили на конкурс цветоводов корзины выращенных ими роз, маргариток и анютиных глазок. Девочка, вырастившая маргаритки, обратила внимание Розы на то, что ни у одной из девочек имя не совпадает с названием любимых цветов.
Какие цветы вырастила каждая из девочек?
[ Ответ ]
5.24. Виновник ночного дорожно-транспортного происшествия скрылся с места аварии.
Первый из опрошенных свидетелей сказал работникам ГАИ, что это были “Жигули”, первая цифра номера машины единица.
Второй свидетель сказал, что машина была марки “Москвич”, а номер начинался с семёрки.
Третий свидетель заявил, что машина была иностранная, номер начинался не с единицы.
При дальнейшем расследовании выяснилось, что каждый из свидетелей правильно указал либо только марку машины, либо только первую цифру номера.
Какой марки была машина и с какой цифры начинался номер?
[ Ответ ]
5.27. На очередном этапе автогонок “Формула 1” первые четыре места заняли Шумахер, Алези, Хилл и Кулхардт. Опоздавший к месту награждения телерепортёр успел заснять пилотов, занявших второе и третье места, которые поливали друг друга шампанским. В это время Шумахер с четвёртым гонщиком пожимали друг другу руки. Далее в кадр попал мокрый Хилл, поздравляющий пилота, занявшего второе место. Напоследок оператор снял сцену, в которой Шумахер и Кулхардт пытались втащить на пьедестал почёта пилота, занявшего четвёртое место.
Просматривая отснятый материал, режиссёр спортивного выпуска быстро разобрался, кто из пилотов какое место занял. Он знал, что, в соответствии с церемонией награждения победителей гонок, пилоты, занявшие первые три места, поливают друг друга шампанским из огромных бутылок знаменитой фирмы спонсора соревнований.
Какое же место занял каждый пилот?
[ Ответ ]
5.28. В некотором царстве-государстве повадился Змей Горыныч разбойничать. Послал царь четырёх богатырей погубить Змея, а награду за то обещал великую. Вернулись богатыри с победой и спрашивает их царь: “Так кто же из вас главный победитель, кому достанется царёва дочь и полцарства?”
Засмущались добры молодцы и ответы дали туманные:
Сказал Илья Муромец: “Это все Алеша Попович, царь-батюшка”.
Алеша Попович возразил: “То был Микула Селянинович”.
Микула Селянинович: “Не прав Алеша, не я это”.
Добрыня Никитич: “И не я, батюшка”.
Подвернулась тут баба Яга и говорит царю: “А прав то лишь один из богатырей, видела я всю битву своими глазами”.
Кто же из богатырей победил Змея Горыныча?
[ Ответ ]
5.29. При составлении расписания на пятницу были высказаны пожелания, чтобы информатика была первым или вторым уроком, физика первым или третьим, история вторым или третьим.
Можно ли удовлетворить одновременно все высказанные пожелания?
[ Ответ ]
5.30. Обсуждая конструкцию нового трёхмоторного самолёта, трое конструкторов поочередно высказали следующие предположения:
1) при отказе второго двигателя надо приземляться, а при отказе третьего можно продолжать полёт;
2) при отказе первого двигателя лететь можно, или при отказе третьего двигателя лететь нельзя;
3) при отказе третьего двигателя лететь можно, но при отказе хотя бы одного из остальных надо садиться.
Лётные испытания подтвердили правоту каждого из конструкторов. Определите, при отказе какого из двигателей нельзя продолжать полёт.
[ Ответ ]
5.31. В соревнованиях по плаванию участвовали Андрей, Виктор, Саша и Дима. Их друзья высказали предположения о возможных победителях:
1) первым будет Саша, Виктор будет вторым;
2) вторым будет Саша, Дима будет третьим;
3) Андрей будет вторым, Дима будет четвёртым.
По окончании соревнований оказалось, что в каждом из предположений только одно из высказываний истинно, другое ложно.
Какое место на соревнованиях занял каждый из юношей, если все они заняли разные места.
[ Ответ ]
5.32. Для длительной международной экспедиции на околоземной космической станции надо из восьми претендентов отобрать шесть специалистов: по аэронавтике, космонавигации, биомеханике, энергетике, медицине и астрофизике. Условия полёта не позволяют совмещать работы по разным специальностям, хотя некоторые претенденты владеют двумя специальностями. Обязанности аэронавта могут выполнять Геррети и Нам; космонавигатора Кларк и Фриш; биомеханика Фриш и Нам; энергетика Депардье и Леонов; врача Депардье и Хорхес; астрофизика Волков и Леонов.
По особенностям психологической совместимости врачи рекомендуют совместные полеты Фриша и Кларка, а также Леонова с Хорхесом и Депардье. Напротив, нежелательно, чтобы Депардье оказался в одной экспедиции с Намом, а Волков с Кларком.
Кого следует включить в состав экспедиции?
[ Ответ ]
ПРАКТИЧЕСКАЯ РАБОТА. ВЫСКАЗЫВАНИЯ С КВАНТОРАМИ. ОТРИЦАНИЕ ВЫСКАЗЫВАНИЙ И ВЫСКАЗЫВАТЕЛЬНЫХ ФОРМ
Цель. Рассмотреть правила определения значения истинности составного высказывания и высказывательных форм с кванторами.
Теоретическая часть
Вопросы к изучению
1. Высказывания с кванторами.
2. Истинность высказываний с кванторами.
3. Отрицание высказываний и высказывательных форм.
Основные понятия темы
Ø квантор общности;
Ø квантор существования;
Ø отрицание высказываний и высказывательных форм.
Правила
Ø нахождения множества истинности составных высказывательных форм:
Т А Ù В = ТА Ç Т В, Т А Ú В = ТА È Т В, 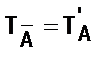
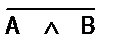
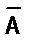
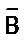

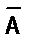
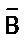
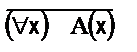
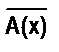
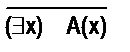
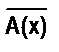
Обозначения
» х – «для всякого х», квантор общности;

Практическая часть
1. В высказывании «всякий прямоугольник является четырехугольником» выделите квантор и высказывательную форму. Переформулируйте данное высказывание, заменив слово «всякий» его синонимом.
2. В высказывании «хотя бы одно из чисел первого десятка составное» выделите квантор и высказывательную форму. Переформулируйте данное высказывание, заменив квантор «хотя бы одно» его синонимом.
3. Прочитайте следующие записи, заменив символические обозначения кванторов общности и существования их словесными выражениями: а) («х ÎR) х 2 – 1 = (х+1) (х-1); б) ($ у Î R) 5 + у =5; в) («у ÎR) у + 3 > 0; г) ($ х Î N) х +3 2 + вх +с = 0 имеет хотя бы один корень.
5. Запишите, используя символы, следующие высказывания и определите их значение истинности: а) Всякое число, умноженное на нуль, есть нуль; б) Произведение любого числа и единицы равно этому числу; в) При делении нуля на любое другое число получается нуль; г) Квадрат любого числа неотрицателен.
6. Установите, какие из нижеприведенных высказываний истинны, а какие ложны: а) Во всяком четырехугольнике диагонали равны; б) Существуют числовые выражения, значения которых нельзя найти; в) При делении на 5 некоторых натуральных чисел в остатке получается 7; г) Любое однозначное число является решением неравенства х + 2 > 1.
7. Докажите или опровергните следующие высказывания: а) Существуют уравнения, множество решений которых пусто; б) Всякое целое число является натуральным; в) Сумма любых двух четных чисел есть число четное; г) Хотя бы одно натуральное число является решением уравнения 7: х =2.
8. Данные ниже высказывания взяты из учебников математики для начальных классов. Выясните, какие из них содержат (в явном или неявном виде) квантор и как следует устанавливать их значение истинности (указать только способ и обосновать его выбор): а) От перестановки слагаемых сумма не изменяется; б) Два соседних слагаемых можно заменять их суммой; в) Площадь прямоугольника равна произведению его длины на ширину; г) Существуют четные числа; д) Некоторые числа делятся на 4; е) Среди многоугольников есть треугольники.
9. Сформулируйте отрицания следующих предложений: а) Число 123 делится на 9; б) При делении числа 32 на 5 в остатке получится 7; в) 3+2 в, в > а; г) существуют две непараллельные прямые; д) у всех прямоугольников все углы прямые; е) ни для какого натурального числа а не найдется натуральное число в такое, что а + в
Конспект урока по информатике на тему «Сложные высказывания. Построение таблиц истинности сложных высказываний.кие операции»
Тема: Сложные высказывания. Построение таблиц истинности сложных высказываний.
ü ввести понятие простых и сложных высказываний;
ü сформировать у учащихся умение определять формы сложных высказываний;
ü сформировать у учащихся умение строить таблицы истинности сложных высказываний.
1. Проверка домашнего задания. Фронтальный опрос.
2. Изучение нового материала.
3. Выполнение заданий на закрепление.
4. Домашнее задание.
I. Проверка домашнего задания. Фронтальный опрос.
1) Что такое логическая операция? ( Логическая операция – способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.)
3) Постройте таблицу истинности для инверсии.
4) Как образуется конъюнкция? ( образуется соединением двух высказываний в одно с помощью союза «и»)
5) Постройте таблицу истинности для конъюнкции.
6) Как образуется дизъюнкция? ( образуется соединением двух высказываний в одно с помощью союза «или»)
7) Постройте таблицу истинности для дизъюнкции.
9) Постройте таблицу истинности для импликации.
10) Как образуется эквивалентность? ( образуется соединением двух высказываний в одно при помощи оборота речи «. тогда и только тогда, когда. »)
11) Постройте таблицу истинности для эквивалентности.
Задания для самостоятельного выполнения. Логические операции.
1. Среди следующих высказываний укажите составные; выделите в них простые, обозначив каждое их них буквой; запишите с помощью логических операций каждое составное высказывание.
3) Земля имеет форму шара. (Это простое высказывание, А= «Земля имеет форму шара»)
2. Ниже приведена таблица, левая колонка которой содержит основные логические союзы (связки), с помощью которых в естественном языке строятся сложные высказывания. Заполните правую колонку таблицы соответствующими названиями логических операций.
Разработка урока «Построение отрицаний высказываний»
Просмотр содержимого документа
«Разработка урока «Построение отрицаний высказываний»»
ОБПОУ «Советский социально-аграрный техникум имени В.М.Клыкова».
Тема: Построение отрицаний высказываний.
Учебная дисциплина: ЕН.01. Математика
Специальность: 44.02.03. Педагогика дополнительного образования
Выполнила: преподаватель ОБПОУ «Советский социально-аграрный техникум имени В.М. Клыкова» Горбовская Т.Л.
Тема урока: Построение отрицаний высказываний.
Цель урока: Способствовать: формированию умения строить отрицания высказываний; обучению навыкам самостоятельного решения задач; развитию умения применять теоретические факты при решении задач;
Содействовать формированию навыков групповой работы, умения представлять свое решение, совместно устранять недочеты в решении; совершенствованию навыков монологической речи, приобретению умения видеть и исправлять недочеты своего доклада.
Создавать условия для развития критичности мышления.
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 4. Осуществлять поиск, анализ и оценку информации, необходимой для постановки и выполнения профессиональных задач, профессионального и личностного развития.
Тип урока: практический.
Форма проведения: математический бой
Оборудование: листы с распечатанными задачами, памятки для участников.
Организация начала урока.
Инструктаж по проведению математического боя.
Подведение итогов. Домашнее задание.
Организация начала урока. Сообщение целей и задач урока.
Инструктаж по проведению математического боя.
Учебная группа делится на две команды. Выбирается капитан каждой команды. Заранее готовятся преподавателем члены жюри (из числа обучающихся). Команды получают условия задач и время на их решение. Команды могут использовать записи в тетрадях, но не имеют права общаться по поводу решения задач ни с кем, кроме жюри. По истечении времени решения задач начинается бой, когда команды в соответствии с правилами рассказывают друг другу решение задач.
Если одна команда рассказывает решение, то другая оппонирует его, то есть ищет в нем ошибки или недостатки, и, если решения нет, то приводит свое. При этом выступление оппонента и докладчика оцениваются жюри в баллах (за решение и оппонирование). Если команды, обсудив предложенное решение, все – таки до конца задачу не решили или не обнаружили допущенные ошибки, то часть баллов (или все баллы) забирает себе жюри. Побеждает команда, которая по окончании боя набирает больше баллов.
Бой состоит из нескольких раундов. В начале каждого раунда одна из команд вызывает другую на одну из задач, решение которой еще не рассматривалось. После этого вызванная команда сообщает, принимает ли она вызов. Если вызов принят, то команда выставляет докладчика (который рассказывает и при необходимости записывает на доске) решение задачи, а вызвавшая команда выставляет оппонента, обязанность которого – искать ошибки. Если команда вызов не принимает, то докладчика обязана выставить та команда, которая сделала вызов, а команда отказавшаяся отвечать, выставляет оппонента. Если же команда, которая сделала вызов тоже отказывается рассказывать решение задачи, то ее вызов считается некорректным. Некорректным считается вызов и в том случае, если вызвавшая команда рассказала решение, но с ним не согласился оппонент, и это несогласие подтвердило жюри.
В начале раунда докладчик рассказывает решение. Доклад должен содержать ответ на все поставленные вопросы и доказательство правильности и полноты полученных ответов. Время доклада ограничивается 4 минутами.
Пока доклад не окончен, оппонент может задать вопросы докладчику только с согласия докладчика, но имеет право просить повторения части решения или разрешить докладчику не доказывать какие – то очевидные с точки зрения оппонента факты. После окончания доклада оппонент имеет право задавать вопросы докладчику.
Оппонент имеет право:
признать решение правильным;
решение (ответ) в основном правильным, но имеющим недостатки и (или) пробелы с обязательным их указанием;
признать решение (ответ) неправильным с указанием ошибок.
Если оппонент согласился с решением, то он и его команда в этом раунде больше не участвуют.
Оппонент обязан формулировать свои вопросы в вежливой, корректной форме; критикуя доклад, не допускать критики обидчика; повторять и уточнять свои вопросы по просьбе докладчика и жюри.
По окончании диалога докладчика и оппонента жюри задает свои вопросы. При необходимости оно может вмешиваться раньше.
Если оппонент доказал, что у докладчика нет решения, то оппонент получает право представить свое решение. При этом бывший докладчик становится оппонентом и может зарабатывать баллы за оппонирование.
Смена раундов влечет за собой смену вызывающей команды.
Каждый член команды имеет право выйти к доске в качестве докладчика или оппонента не больше двух раз за весь бой. Команда имеет право не более двух раз за бой заменять докладчика или оппонента, но при этом выход засчитывается как тому, кого заменили, так и тому, кто вышел на замену.
В любой момент боя команда, которая должна вызывать, может отказаться сделать это (если нет решения задач). Тогда другая команда получает право (но не обязана) рассказывать решение оставшихся задач. При этом вторая команда выставляет оппонентов и может получать баллы за оппонирование, но рассказывать решение она не имеет права.
Право первого вызова устанавливается конкурсом капитанов, который проводится в начале боя.
Каждая задача оценивается в 12 баллов, которые по итогам раунда распределяются между докладчиком, оппонентом и жюри. Если докладчик представил правильное и полное решение, то все 12 баллов достаются ему. Если же оппонент доказал, что докладчик не дал решения задачи, то происходит «смена ролей».
Размер штрафа за некорректный вызов объявляется командам до боя (до 6 баллов). Жюри является верховным толкователем правил боя. Решения жюри являются обязательными для команд.
Во время боя только капитан может от имени команды обращаться к жюри и соперникам: сообщать о вызове или отказе и т.д. если капитан у доски, то он оставляет за себя заместителя, исполняющего в это время обязанности капитана. Имена капитана и заместителя сообщаются жюри до начала боя. Во время решения задач главная обязанность капитана – координировать действия членов команды так, чтобы имеющимися силами решить как можно больше задач. Капитан с учетом пожеланий членов команды распределяет между ними задачи для решения, следит, чтобы каждая задача кем – то решалась, организует проверку найденных решений. Капитан заранее выясняет, кто будет докладчиком или оппонентом на той или иной задаче.
Жюри ведет на доске протокол боя. Если одна из команд не согласна с принятым жюри решением по задаче, то она имеет право немедленно потребовать перерыв на несколько минут для разбора ситуации с участием Председателя жюри.
После начала следующего раунда счет предыдущего раунда не может быть изменен. Жюри также следит за порядком во время боя (может оштрафовать команду за шум, некорректное поведение, общение со своим представителем, находящимся у доски).
Командам предлагаются следующие задачи (распечатаны для каждого участника):
Сформулируйте, используя законы де Моргана, отрицания следующих утверждений:
а) Четырехугольник ABCD – прямоугольник или параллелограмм.
б) Число 12 четное и делится на 3.
в) Число 28 нечетное или не делится на 4.
Какие из нижеприведенных предложений являются отрицанием высказывания «Все натуральные числа кратны 5»; свой выбор обоснуйте:
а) Все натуральные числа не кратны 5.
б) Существуют натуральные числа, не кратные 5.
в) Существуют натуральные числа, кратные 5.
г) Неверно, что все натуральные числа кратны 5.
д) Не все натуральные числа кратны 5.
Постройте двумя способами отрицание высказывания:
а) Всякое свойство квадрата присуще прямоугольнику.
б) Некоторые простые числа являются четными.
Определите, являются данные предложения отрицаниями друг друга, или нет; объясните почему:
а) Число 12 четное, число 12 – нечетное.
б) Все простые числа нечетны. Все простые числа четны.
в) Все простые числа нечетны. Существуют четные простые числа.
г) Некоторые углы острые. Некоторые углы тупые.
Переформулируйте данные предложения так, чтобы они не содержали слов «неверно, что», но имели тот же смысл:
а) Неверно, что число 9 – четное или простое.
б) Неверно, что треугольник ABC – равнобедренный и прямоугольный.
в) Неверно, что каждый четырехугольник является прямоугольником.
г) Неверно, что хотя бы в одном прямоугольнике диагонали взаимно перпендикулярны.
Постройте отрицания следующих высказываний и выясните, что истинно – данное высказывание или его отрицание:
а) Среди чисел есть такие, которые делятся на 5 и на 7.
б) Существуют числовые выражения, значения которых нельзя найти.
в) Частное чисел 25842 и 6 меньше разности чисел 14150 и 9833.
Сформулируйте отрицания следующих предложений двумя способами:
а) Число 123 делится на 9.
б) При делении числа 32 на 5 в остатке получится 7.
г) Треугольник ABC – прямоугольный.
Сформулируйте предложения, которые начинаются словами «неверно, что» и имеют тот же смысл, что и данные:
а) Прямые AB и CD не параллельны и не пересекаются;
б) Стороны четырехугольника ABCD не параллельны или не равны;
в) Существуют уравнения, не имеющие действительных корней;
г) Все прямоугольники не имеют равных смежных сторон.
Проводится конкурс капитанов, который не приносит очков, но даёт право вызова команде.
Вопрос для капитанов:
Как проверить, правильно ли построено отрицание высказывания?
В ходе математического боя оценивается не только работа команды, но и работа каждого участника команды (преподаватель ведет протокол).
Оценка каждого участника команды складывается из результатов защиты решения задачи (роль докладчика), работы в качестве оппонента, оценки команды.
Выступление жюри. Подведение итогов урока преподавателем. Отметки за урок.
Постройте двумя способами отрицание высказывания:
Произведение чисел 4070 и 8 меньше, чем сумма чисел 18396 и 14174;
Среди различных прямоугольников есть такие, площади которых равны.
Постройте отрицания следующих высказываний и выясните, что истинно – данное высказывание или его отрицание:
Сумма двух любых четных чисел есть число четное;
Хотя бы одно натуральное число является решением уравнения 7:х=2;
При делении числа 58 на 7 в остатке получится 3 или 7.

