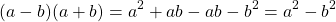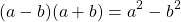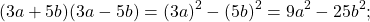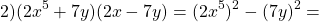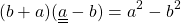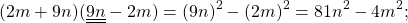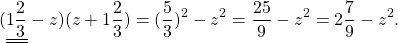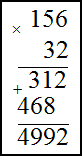Произведение суммы чисел что это
Как легко понять знаки Σ и П с помощью программирования
Для тех, кто подзабыл матешу
Вот говорят, что если ты не закончил Физтех, ФПМ или Бауманку, тебе в программировании делать нечего. Почему так говорят? Потому что, дескать, ты не учил сложную математику, а в программировании без неё никуда.
Это всё чушь, конечно. Если вы плохо знаете математику, вы можете быть блестящим разработчиком. Вы вряд ли напишете драйверы для видеокарты, но вы запросто сделаете мобильное приложение или веб-сервис. А это — основные деньги в этой среде.
Но всё же, чтобы получить некоторое интеллектуальное превосходство, вот вам пара примеров из страшного мира математики. Пусть они покажут вам, что не все закорючки в математике — это ад и ужас. Вот две нестрашные закорючки.
Знак Σ — сумма
Когда математикам нужно сложить несколько чисел подряд, они иногда пишут так:
Σ (читается «сигма») — это знак алгебраической суммы, который означает, что нам нужно сложить все числа от нижнего до верхнего, а перед этим сделать с ними то, что написано после знака Σ.
На картинке выше написано следующее: «посчитать сумму всех чисел от 5 до 15, умноженных на два». То есть:
Давайте для закрепления ещё один пример. На картинке ниже будет сказано «Найди сумму квадратов чисел от 5 до 10». То есть «возьми все числа от 5 до 10, каждое из них возведи в квадрат, а результаты сложи».
Но мы с вами как программисты видим, что здесь есть повторяющиеся действия: мы много раз складываем числа, которые меняются по одному и тому же правилу. А раз мы знаем это правило и знаем, сколько раз надо его применить, то это легко превратить в цикл. Для наглядности мы показали, какие параметры в Σ за что отвечают в цикле:
Произведение П
С произведением в математике работает точно такое же правило, только мы не складываем все элементы, а перемножаем их друг на друга:
А если это перевести в цикл, то алгоритм получится почти такой же, что и в сложении:
Что дальше
Сумма и произведение — простые математические операции, пусть они и обозначаются страшными символами. Впереди нас ждут интегралы, дифференциалы, приращения и бесконечные ряды. С ними тоже всё не так сложно, как кажется на первый взгляд.
math4school.ru
Суммы и произведения
Немного теории
При решении олимпиадных задач о суммах и произведениях чисел сочетаются различные соображения, связанные с применением:
Задачи с решениями
где b – рациональное число, n – натуральное число.
Умножим и разделим левую часть равенства на
В числителе в результате последовательного применения формулы разности квадратов двух выражений получим
Следовательно, левая часть равенства равна
В правой части записана сумма (2n+1)-го первого члена геометрической прогрессии с первым членом – 1, и знаменателем – b. Эта сумма равна
Следовательно, равенство верно.
– n 2 + (n + 1) 2 = n + (n + 1),
3. Докажите, что сумма
Преобразуем второе слагаемое данной суммы так:
где k – некоторое натуральное число. Мы видим, что данная сумма равна 4003·k и, следовательно, делится на 4003. (Заметим, что 4003 – простое число, и поэтому при установлении делимости на 4003 необходимо выделять множитель 4003.)
Обозначим требуемую сумму через S. Представим каждое из слагаемых заданной суммы следующим образом:
Складывая почленно эти представления, имеем
| S = | 1 | · ( | 1 – | 1 | ) = | n | . |
| 4 | 4n + 1 | 4n + 1 |
5. Вычислите коэффициент при х 100 в многочлене
после приведения всех подобных слагаемых.
Перемножив без приведения подобных членов три многочлена
получим сумму произведений вида
где р, q, r – целые числа, удовлетворяющие условиям
0 p 100, 0 q 100, 0 r 100,
причем коэффициенты при х p х q х r равны 1. Выражение х 100 получится только тогда, когда
Следовательно, искомый коэффициент равен числу целочисленных решений уравнения
0 p 100, 0 q 100, 0 r 100.
Это уравнение имеет
101 решение при р = 0,
100 решений при р = 1,
99 решений при р = 2
Следовательно, число всех решений равно
6. Доказать, что число
(2010·2011·2012·2013 + 1)·(2011·2012·2013·2014 + 1)·(2012·2013·2014·2015 + 1)
есть полный квадрат.
Полагая в первом множителе n = 2012, его можно преобразовать следующим образом:
2010·2011·2012·2013 + 1 = (n – 2)·(n – 1)·n·(n + 1) + 1 =
Подобным образом убеждаемся, что два других множителя данного произведения тоже являются квадратами. Но
что и требовалось доказать.
7. Докажите, что при условии А + В + С = 180° имеет место равенство
ctg A · ctg B + ctg В · ctg C + ctg С · ctg А = 1.
| ctg A · ctg B + ctg В · ctg C + ctg С · ctg А = |
| = | cos A · cos B | + | cos B · cos C | + | cos C · cos A | = |
| sin A · sin B | sin B · sin C | sin C · sin A |
| = | cos A · cos B · sin C + cos B · cos C · sin A + cos C · cos A · sin B | = |
| sin A · sin B · sin C |
| = | cos A · cos B · sin C + cos C · sin (A + В) | = |
| sin A · sin B · sin C |
| = | cos C · sin (A + В) + sin C · (cos A · cos B – sin A · sin B) | + | sin A · sin B · sin C | = |
| sin A · sin B · sin C | sin A · sin B · sin C |
| = | sin (A + B + C) + sin A · sin B · sin C | = | sin 180° | + 1 = 1. |
| sin A · sin B · sin C | sin A · sin B · sin C |
Преобразования законны, если ни один из синусов А, В, С не равен 0, т.е. ни один из углов А, В, С не равен 180°·k, где k – целое число.
Следовательно, справедливы неравенства
Перемножая почленно эти неравенства, получаем
Отсюда и из равенств
следует требуемое неравенство.
Посмотрим, сколько раз входит каждое число от 2 до 100 в наше произведение. Число 2 входит во все факториалы, начиная со второго, то есть 99 раз; число 3 входит во все факториалы, начиная с третьего, то есть 98 раз; и так далее – каждое число входит во все факториалы, начиная со »своего». То есть n входит в произведение (101 – n) раз:
В частности, все нечётные числа входят в произведение чётное число раз, а чётные – нечётное число раз. Выделим отдельно произведение всех чётных чисел, взятых по одному разу,
В первой скобке все степени чётные, значит, произведение чисел в первых скобках — квадрат целого числа. А произведение чисел во вторых скобках равно
Но 2 50 является квадратом целого числа. Значит, если зачеркнуть 50!, то оставшееся произведение будет квадратом целого числа.
Ответ: д а, нужно вычеркнуть 50!.
10. На какую наибольшую степень тройки делится произведение
= 3 10 ·1·11·111·1111·11111·111111·1111111·11111111·111111111·1111111111.
Задачи без решений
5. Докажите, что произведение ста последовательных натуральных чисел не может быть сотой степенью натурального числа.
Произведение суммы и разности
Произведение суммы и разности двух выражений можно найти как произведение многочленов. Для ускорения вычислений удобнее вывести формулу.
Найдем произведение суммы и разности двучленов непосредственным умножением:
-ab и +ab — противоположные слагаемые, поэтому их сумма равна нулю.
Произведение суммы и разности двух выражений равно разности квадратов этих выражений.
Формула произведения суммы и разности:
Произведение суммы и разности двух выражений можно изобразить схематически так:
Рассмотрим на примерах, как находить произведение суммы и разности двух выражений с помощью схемы и с помощью формулы.
Если все, что стоит до «+» и до «-«, заключить в квадрат, все, что после этих знаков — в круг, то произведение суммы (3a+5b) и разности (3a-5b) с помощью схемы можно представить так:
Чтобы применить форму произведения суммы разности, найдем a и b. В данном примере a=3a, b=3b:
Важно помнить — при возведении в квадрат произведения нескольких множителей, дроби или степени их обязательно следует записывать в скобках!
Как найти произведение суммы и разности, если слагаемые в скобках поменять местами?
От перестановки мест слагаемых сумма не меняется. Поэтому в разности квадратов на первое месте нужно поставить то выражение, которое стоит на первом месте в разности. Например,
Что такое произведение чисел
Определение произведения чисел
Задание. Найти произведение чисел:
1) 1.2$\cdot 3$ ; 2) 4$\cdot 5 \cdot 13$
Ответ.
$4 \cdot 5 \cdot 13=260$
Свойства произведения чисел
На основании этих свойств можем заключить, что при перестановке множителей значение произведения не меняется.
Что такое произведение чисел не по зубам? Тебе ответит эксперт через 10 минут!
Задание. Найти произведение чисел удобным способом:
1) 5$\cdot 17 \cdot 2$ ; 2) 7$\cdot 2 \cdot 15 \cdot 5$
Решение. По свойства умножения имеем:
$$5 \cdot 17 \cdot 2=(5 \cdot 2) \cdot 17=10 \cdot 17=170$$
$$7 \cdot 2 \cdot 15 \cdot 5=(7 \cdot(2 \cdot 15)) \cdot 5=(7 \cdot 30) \cdot 5=210 \cdot 5=1050$$
Ответ.
$5 \cdot 17 \cdot 2=170$
$7 \cdot 2 \cdot 15 \cdot 5=1050$
Если устное умножение чисел затруднительно используют умножение в столбик. В столбик можно умножать большие натуральные числа или десятичные дроби.
Задание. Найти произведение чисел
Решение. Запишем умножаемые числа в столбик. Далее умножим сначала единицы второго числа на первое, полученное произведение запишем под чертой. Затем аналогично умножим десятки второго числа на первое. Результат запишем под первым произведением только на один разряд левее. В конце найдем сумму полученных произведений по правилу сложения в столбик
Числа. Произведение чисел. Свойства умножения.
Умножение — одно из четырёх основных арифметических действий, бинарная математическая операция, в которой один аргумент складывается столько раз, сколько показывает другой.
Произведение чисел m и n — это сумма n слагаемых, каждое из этих слагаемых = m.
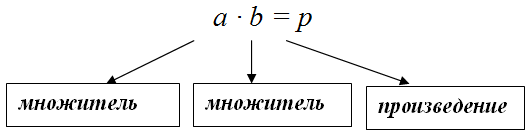
Выражение типа m • n, и значение такого выражения называется произведение чисел m и n. Числа m и n называются множителями.
Если устное умножение чисел затруднительно используют умножение в столбик. В столбик можно умножать большие натуральные числа или десятичные дроби.
Свойства умножения чисел.
1. Коммутативность:
При перестановке множителей местами, значение произведения остается без изменений. Это переместительное свойство умножения.
где, 3 и 4 — множители, а 12 — произведение.
2. Ассоциативность:
В произведении 3-х и больше множителей при перестановке этих множителей либо изменения последовательности выполнения умножения результат остается одинаковым.
3. Дистрибутивность:
4. Произведение всякого натурального числа и единицы, будет соответствовать этому числу.
Произведение всякого натурального числа и нуля, = 0.
Выражения с буквенными множителями записывают так:
Кроме того, не используют знак умножения и перед скобками,
2 • (a + b) записывают как 2(а + b),