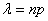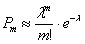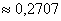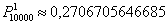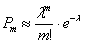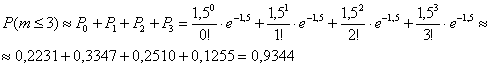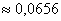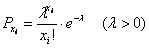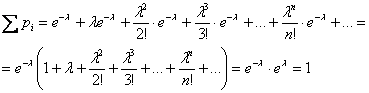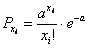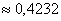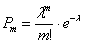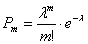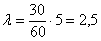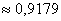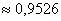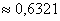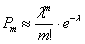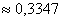Принято считать что распределение населения по доходам соответствует распределение пуассона
Распределение Пуассона и формула Пуассона
Краткая теория
Для пуассоновской случайной величины математическое ожидание и дисперсия совпадают с интенсивностью потока событий:
$$M(X)=lambda, quad D(X)=lambda.$$
Распределение Пуассона – определение
Распределение Пуассона — вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга. Другими словами, если событие происходит с некоторой периодичностью, то мы можем определить вероятность, что такое событие произойдёт n раз за интересующий нас период.
Параметр лямбда – λ
Распределение Пуассона зависит только от одного параметра – λ, данный параметр зависит от вероятности успешного события и общего количества событий.
Успешное событие: распределение Пуассона применяется только тогда, когда есть разделение на результат “да” и “нет”, например, лампочка перегорела: да – успешное событие; шина прокололась: да – успешное событие и так далее.
λ = n*p, где p – вероятность успешного события, а n – общее количество событий, для которых ведётся расчёт.
Например, если гроза проходит раз в месяц и мы хотим посчитать вероятность грозы за 24 месяца, то вероятность равна единице, а количество событий равно 24, откуда лямбда равна 24.
Можно считать по-другому, вероятность грозы в конкретный день – 1/30, количество событий – 730 дней, лямбда равна 24.3.
Пример
В тысяче ящиков с антоновками в одном попадается голден, какова вероятность, что в 5000 ящиках будет меньше 4 ящиков с яблоком голден?
Вероятность ящика с яблоком голден – 0.1% (1 ящик на 1000 = 1/1000, если в процентах – 1/1000 * 100 = 0.1%)
Общее количество событий – 5000 ящиков
Из вышесказанного следует:
λ = 5000 * 0.001 = 5
Функция вероятности (формула Пуассона)
Вероятность, что успешное событие произойдёт k раз:
Пример
В тысяче ящиков с антоновками в одном попадается голден, какова вероятность, что в 5000 ящиках будет 2 ящика с яблоком голден?
Из предыдущего примера мы знаем, что λ=5, теперь мы ищем вероятность, что k будет равно 2, для этого используем формулу функции вероятности:
Условия возникновения распределения Пуассона
Рассмотрим условия, при которых возникает распределение Пуассона.
Во-первых, распределение Пуассона является предельным для биномиального распределения, когда число опытов n неограниченно увеличивается (стремится к бесконечности) и одновременно вероятность p успеха в одном опыте неограниченно уменьшается (стремится к нулю), но так, что их произведение np сохраняется в пределе постоянным и равным λ (лямбде):

В математическом анализе доказано, что распределение Пуассона с параметром λ = np можно приближенно применять вместо биномиального, когда число опытов n очень велико, а вероятность p очень мала, то есть в каждом отдельном опыте событие A появляется крайне редко.
Во-вторых, распределение Пуассона имеет место, когда есть поток событий, называемым простейшим (или стационарным пуассоновским потоком). Потоком событий называют последовательность таких моментов, как поступление вызовов на коммуникационный узел, приходы посетителей в магазин, прибытие составов на сортировочную горку и тому подобных. Пуассоновский поток обладает следующими свойствами:
Характеристики случайной величины, распределённой по закону Пуассона
Характеристики случайной величины, распределённой по закону Пуассона:
математическое ожидание 
стандартное отклонение 
дисперсия 
Распределение Пуассона и расчёты в MS Excel
Вероятность распределения Пуассона P(m) и значения интегральной функции F(m) можно вычислить при помощи функции MS Excel ПУАССОН.РАСП. Окно для соответствующего расчёта показано ниже (для увеличения нажать левой кнопкой мыши).
MS Excel требует ввести следующие данные:
Почему Пуассон изобрел свое распределение?
Чтобы предсказывать количествобудущихсобытий!
Или более формально: чтобы предсказывать вероятность данного числа событий, происходящих в определенный интервал времени.
В продажах, например, “событие” это покупка (сам момент покупки, не просто выбор). Событием может быть количество посетителей в день на веб-сайте, кликов на рекламном объявлении в следующем месяце, число звонков в рабочее время или число людей, которые умрут от смертельных заболеваний в следующем году, и так далее.
Недостатки биномиального распределения
a) Биномиальная случайная величина бинарна — 0 или 1.
В примере выше у нас было 17 лайков в неделю. Это 17/7 = 2.4 человека в день и 17/(7*24) = 0.1 в час.
Если моделировать вероятность успеха в часах (0.1 человек в час), используя биномиальную случайную величину, получим, что в большем количестве часов лайков будет 0, а в некоторые часы ровно 1 лайк. Также возможно, что в час будет больше 1 лайка (2, 3, 5 и т.д.).
Проблема с биномиальным распределением в том, что оно не может содержать более одного события в единицу времени (1 час в примере).
Так может разделить 1 час на 60 минут и принять за единицу времени минуту? Тогда в 1 час поместится несколько событий. (Помним, что 1 минута содержит только ноль или одно событие).
Теперь проблема решена?
Вроде бы. Но что если в течение одной минуты мы получим несколько лайков? (например, кто-то поделился постом в Твиттере, и трафик вырос в эту минуту). Что тогда? Можно разделить минуту на секунды. Тогда единицей времени становится секунда, и в минуту помещается несколько событий. Но проблема бинарного контейнера будет существовать для все меньших единиц времени.
Дело в том, что биномиальная случайная величина может содержать несколько событий, если делить единицу времени на все меньшие единицы. В результате изначальная единица времени будет содержать более одного события.
Математически это означает n → ∞. Если предположим, что среднее значение фиксировано, тогда p → 0. В противном случае n*p — количество событий — чрезмерно возрастет.
Единица времени с использованием этого лимита может быть бесконечно мала. Больше не нужно беспокоиться о более чем одном событии в единицу времени. Так получается распределение Пуассона.
b) В биномиальном распределении количество попыток (n) должно быть известно заранее.
Нельзя посчитать вероятность успеха при помощи биномиального распределения, зная только среднее значение (17 человек в неделю). Нужно больше информации (n и p), чтобы использовать формулу.
Распределение Пуассона же не обязывает вас знать ни n ни p. Предположим, что n бесконечно велико, а p бесконечно мала. Единственный параметр распределения — значение λ (ожидаемое значение x). В реальной жизни чаще известно только значение (например, с 2 до 4 часов дня я принял 3 телефонных звонка), а не значения n и p.
Решение задачи на распределение Пуассона в Excel
Пример 1. Отдел технического контроля определил, что среднее число не соблюденных допусков в размерах производимых деталей составляет 6. Определить вероятности следующих событий обеими рассматриваемыми функциями (для сравнения результатов вычислений):
Вид таблицы данных:
Рассчитаем вероятность наличия трех и менее дефектов с помощью функций:
Для нахождения вероятности выбора детали с наличием ровно трех дефектов используем функции:
Для расчета вероятности точного совпадения третий аргумент задан в качестве логического ЛОЖЬ.
Как видно, результаты вычислений обеих функций идентичны.
Числовые характеристики случайной величины Х
Математическое ожидание распределения Пуассона
M[X] = λ
Дисперсия распределения Пуассона
D[X] = λ
Вероятность появления k событий за время длительностью t можно также найти по формуле Пуассона:
где λ — интенсивность потока событий, то есть среднее число событий, которые появляются в единицу времени.
а) оба элемента будут работать безотказно;
P(2) = P1(0)*P2(0) = 0,8187*0,6065 = 0,4966
б) только один элемент выйдет из строя.
P(1) = P1(0)*(1-P2(0)) + (1-P1(0))*P2(0) = 0.8187*(1-0.6065) + (1-0.8187)*0.6065 = 0.4321
Формула Пуассона
Давайте получим формулу Пуассона математически из формулы функции биномиального распределения.
Что такое распределение Пуассона?
Sep 1, 2019 · 6 min read
Прежде чем вводить параметр λ и подставлять его в формулу, давайте задумаемся: почему Пуассону вообще пришлось изобретать такое распределение?
1. Почему Пуассон изобрел свое распределение?
Чтобы предсказывать количество будущих событий!
Или более формально: чтобы предсказывать вероятность данного числа событий, происходящих в определенный интервал времени.
В продажах, например, “ событие” это покупка (сам момент покупки, не просто выбор). Событием может быть количество посетителей в день на веб-сайте, кликов на рекламном объявлении в следующем месяце, число звонков в рабочее время или число людей, которые умрут от смертельных заболеваний в следующем году, и так далее.
Вот пример, как я использую распределение Пуассона в реальной жизни.
2. Как решить эту задачу?
Давай т е на время сделаем вид, что мы ничего не знаем о распределении Пуассона. Как тогда решить задачу?
Первый путь: начать с количества прочтений. Для каждого читателя блога есть вероятность, что статья ему действительно понравится и он поставит лайк.
Это классическая работа для биномиального распределения, так как мы рассчитываем количество успешных событий (лайков).
Биномиальная случайная величина — это количество успешных x в n повторяющихся попыток. Предполагается, что вероятность успеха p является постоянной в каждой попытке.
Итак, у нас есть только один параметр — 17 человек в неделю, что является “ средним значением” (средним значением успешных событий в неделею, или математическим ожиданием x). Нам ничего не известно ни о вероятности получения лайков p, ни о количестве посетителей блога n.
Значит, нам нужно больше информации для решения задачи. Что конкретно нужно, чтобы оформить эту вероятность как биномиальную проблему? Две вещи: вероятность успеха (лайков) p и количество попыток (посетителей) n.
Получим их из прошлых данных.
Это статистика за 1 год. Общее количество читателей блога — 59 тысяч, 888 из них поставили лайк.
Следовательно, количество читателей в неделю ( n): 59 000/52 = 1134. Количество поставивших лайк в неделю ( x): 888/52 =17.
Используя биномиальную функцию вероятности, посчитаем вероятность того, что я получу точно 20 успешных событий (20 лайков) на следующей неделе.
Только что мы решили задачу с помощью биномиального распределения.
Тогда зачем нам распределение Пуассона? Что оно может делать такого, что не может биномиальное распределение?
3. Недостатки биномиального распределения
a) Биномиальная случайная величина бинарна — 0 или 1.
В примере выше у нас было 17 лайков в неделю. Это 17/7 = 2.4 человека в день и 17/(7*24) = 0.1 в час.
Если моделировать вероятность успеха в часах (0.1 человек в час), используя биномиальную случайную величину, получим, что в большем количестве часов лайков будет 0, а в некоторые часы ровно 1 лайк. Также возможно, что в час будет больше 1 лайка (2, 3, 5 и т.д.).
Проблема с биномиальным распределением в том, что оно не может содержать более одного события в единицу времени (1 час в примере).
Так может разделить 1 час на 60 минут и принять за единицу времени минуту? Тогда в 1 час поместится несколько событий. (Помним, что 1 минута содержит только ноль или одно событие).
Теперь проблема решена?
Вроде бы. Но что если в течение одной минуты мы получим несколько лайков? (например, кто-то поделился постом в Твиттере, и трафик вырос в эту минуту). Что тогда? Можно разделить минуту на секунды. Тогда единицей времени становится секунда, и в минуту помещается несколько событий. Но проблема бинарного контейнера будет существовать для все меньших единиц времени.
Дело в том, что биномиальная случайная величина может содержать несколько событий, если делить единицу времени на все меньшие единицы. В результате изначальная единица времени будет содержать более одного события.
Математически это означает n → ∞. Если предположим, что среднее значение фиксировано, тогда p → 0. В противном случае n*p — количество событий — чрезмерно возрастет.
Единица времени с использованием этого лимита может быть бесконечно мала. Больше не нужно беспокоиться о более чем одном событии в единицу времени. Так получается распределение Пуассона.
b) В биномиальном распределении количество попыток (n) должно быть известно заранее.
Нельзя посчитать вероятность успеха при помощи биномиального распределения, зная только среднее значение (17 человек в неделю). Нужно больше информации ( n и p), чтобы использовать формулу.
Распределение Пуассона же не обязывает вас знать ни n ни p. Предположим, что n бесконечно велико, а p бесконечно мала. Единственный параметр распределения — значение λ (ожидаемое значение x). В реальной жизни чаще известно только значение (например, с 2 до 4 часов дня я принял 3 телефонных звонка), а не значения n и p.
4. Формула Пуассона
Давайте получим формулу Пуассона математически из формулы функции биномиального распределения.
Теперь нужно только показать, что умножение первых двух множителей n!/((n-k)!*n^k) дает 1, когда n стремится к бесконечности.
Распределение и формула Пуассона
В данной статье мы рассмотрим ещё одно дискретное распределение, которое получило широкое распространение на практике. Не успел я открыть курс по теории вероятностей, как сразу стали поступать запросы: «Где Пуассон? Где задачи на формулу Пуассона?» и т.п. И поэтому я начну с частного применения распределения Пуассона – ввиду большой востребованности материала.
Задача до боли эйфории знакома:
– проводится 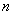
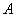
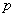
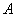
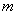
Наверное, вам уже снится формула Бернулли🙂 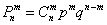
тем более, на уроке о биномиальном распределении вероятностей мы разобрали ситуацию по косточкам.
В том случае, если количество испытаний 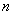
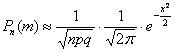
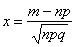
Однако и тут есть «слабое звено» – теорема Лапласа начинает серьёзно барахлить (давать большую погрешность), если вероятность 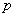
Итак, если количество испытаний 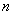
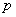
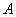
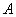
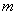
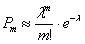
Напоминаю, что ноль факториал 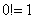
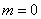
Вместо «лямбды» также используют букву «а».
В новом микрорайоне поставлено 10000 кодовых замков на входных дверях домов. Вероятность выхода из строя одного замка в течение месяца равна 0,0002. Найти вероятность того, что за месяц откажет ровно 1 замок.
Утопичная, конечно, задача, но что делать – решаем🙂
В данном случае количество «испытаний» 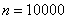
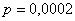
Вычислим:
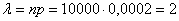
Таким образом:
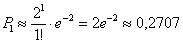
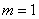
Ответ:
С технической точки зрения этот результат можно получить несколькими способами, расскажу о них в историческом ракурсе:
1) С помощью специальной таблицы, которая до сих пор встречается во многих книгах по терверу. В данную таблицу сведены различные значения 
2) С помощью прямого вычисления на микрокалькуляторе (прогресс!).
3) С помощью стандартной экселевской функции:
=ПУАССОН(m; лямбда; 0)
в данной задаче вбиваем в любую ячейку Экселя =ПУАССОН(1; 2; 0) и жмём Enter.
Следует отметить, что развитие вычислительной техники фактически отправило в историю методы Лапласа, да и рассматриваемый метод тоже – по той причине, что ответ легко вычислить более точно по формуле Бернулли:
Здесь я использовал функцию БИНОМРАСП, о которой неоднократно упоминал ранее.
Но формула Пуассона, тем не менее, даёт очень крутое приближение:
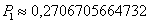
Впрочем, это всё лирика, решать-то всё равно нужно по формуле Пуассона:
Завод отправил в торговую сеть 500 изделий. Вероятность повреждения изделия в пути равна 0,003. Найти вероятность того, что при транспортировке будет повреждено: а) ни одного изделия, б) ровно три изделия, в) более трех изделий.
Решение: используем формулу Пуассона:
В данном случае:
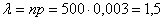
а) 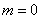
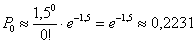
б) 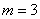
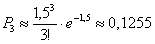
в) 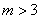
А тут всё немножко хитрее. Сначала найдём 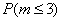
Само собой, ручками это считать надоест, и поэтому я добавил в свой расчётный макет автоматическое построение распределения Пуассона (см. Пункт 7) – пользуйтесь на здоровье.
По теореме сложения вероятностей противоположных событий:
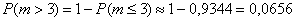
Ответ: а) 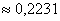
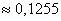
Вероятность изготовления бракованных деталей при их массовом производстве равна 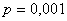
Решение и ответ в конце урока.
Встречаются и другие формулировки условия. Так, в предложенной задаче может идти речь о том, что производственный брак составляет 0,1% или «в среднем 1 деталь на каждую тысячу». Бывает и дано готовое значение «лямбда», например: «В стандартной партии из 800 деталей брак в среднем составляет 0,8 деталей. Найти вероятность того, что в очередной партии…».
В этой связи ни в коем случае не отключаем голову – даже в таких простых примерах!
А теперь о самом распределении Пуассона. Случайная величина 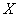
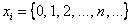
Или, если расписать подробно:
Вспоминая разложение экспоненты в ряд, легко убедиться, что:
В теории установлено, что математическое ожидание пуассоновской случайной величины равно 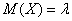
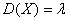
Обратите внимание, что во всех вышеприведённых заданиях мы лишь ПОЛЬЗОВАЛИСЬ распределением Пуассона для приближенного расчёта вероятностей, в то время как ТОЧНЫЕ значения следовало находить по формуле Бернулли, т.е., там имело место биномиальное распределение.
И следующие две задачи принципиально отличаются от предыдущих:
Случайная величина 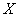
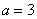
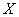
Отличие состоит в том, что здесь речь идёт ИМЕННО о распределении Пуассона.
Решение: случайная величина 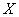
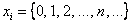
По условию, 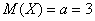
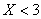
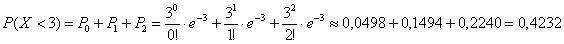
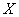
Ответ:
Аналогичная задача на понимание:
Случайная величина 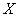
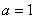
Решение и ответ в конце урока.
Помимо приближения биномиального распределения (Примеры 1-3), распределение Пуассона нашло широкое применение в теории массового обслуживания для вероятностной характеристики простейшего потока событий. Постараюсь быть лаконичным:
Пусть в некоторую систему поступают заявки (телефонные звонки, приходящие клиенты и т.д.). Поток заявок называют простейшим, если он удовлетворяет условиям стационарности, отсутствия последствий и ординарности. Стационарность подразумевает то, что интенсивность заявок постоянна и не зависит от времени суток, дня недели или других временнЫх рамок. Иными словами, не бывает «часа пик» и не бывает «мёртвых часов». Отсутствие последствий означает, что вероятность появления новых заявок не зависит от «предыстории», т.е. нет такого, что «одна бабка рассказала» и другие «набежали» (или наоборот, разбежались). И, наконец, свойство ординарности характеризуется тем, что за достаточно малый промежуток времени практически невозможно появление двух или бОльшего количества заявок. «Две старушки в дверь?» – нет уж, увольте, рубить удобнее по порядку.
Итак, пусть в некоторую систему поступает простейший поток заявок со средней интенсивностью 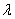
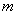
Звонки в диспетчерскую такси представляет собой простейший пуассоновский поток со средней интенсивностью 30 вызовов в час. Найти вероятность того, что: а) за 1 мин. поступит 2-3 вызова, б) в течение пяти минут будет хотя бы один звонок.
Решение: используем формулу Пуассона:
а) Учитывая стационарность потока, вычислим среднее количество вызовов за 1 минуту:
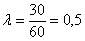
По теореме сложения вероятностей несовместных событий:
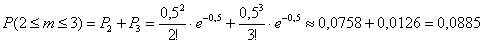
б) Вычислим среднее количество вызов за пять минут:
По формуле Пуассона:
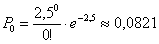
По теореме сложения вероятностей противоположных событий:
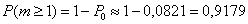
Ответ: а) 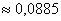
Заметьте, что, несмотря на конечное количество возможных звонков (а оно в принципе конечно), здесь имеет место именно распределение Пуассона, а не какое-то другое.
Для самостоятельного решения:
Среднее число автомобилей, проходящих таможенный досмотр в течение часа, равно 3. Найти вероятность того, что: а) за 2 часа пройдут досмотр от 7 до 10 автомобилей; б) за полчаса успеет пройти досмотр только 1 автомобиль.
Решение и ответ в конце урока.
Наверное, многие знают, что теория массового обслуживания – это обширный и очень интересный раздел прикладной математики, и сейчас мы познакомились с простейшей его задачей.
Дополнительные примеры на распределение и формулу Пуассона можно найти в тематической pdf-книге, и я предлагаю вам ознакомиться с ещё одной популярной вещью – Гипергеометрическим распределением вероятностей.
Приятного и полезного чтения!
Пример 3. Решение: используем формулу Пуассона: 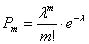
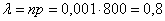
а) 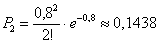
б) По теореме сложения вероятностей несовместных событий: 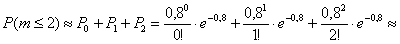
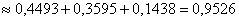
Ответ: а) 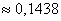
Пример 5. Решение: случайная величина 
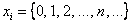
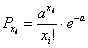
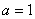
Найдём вероятность того, что случайная величина примет нулевое значение: 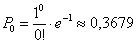
По теореме сложения вероятностей противоположных событий:
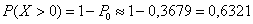
Ответ:
Пример 7. Решение: предполагая поток простым, используем формулу Пуассона:
а) Вычислим 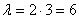
По теореме сложения вероятностей несовместных событий: 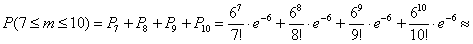
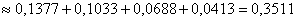
б) Вычислим 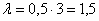
По формуле Пуассона:
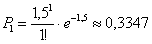
Ответ: а) 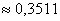
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5