Предел функции что это

Предел функции.

Предел функции – число a будет пределом некоторой изменяемой величины, если в процессе своего изменения эта переменная величина неограниченно приближается к a.

Или другими словами, число A является пределом функции y = f (x) в точке x₀, если для всякой последовательности точек из области определения функции, не равных x₀, и которая сходится к точке x₀ (lim x_n = x0), последовательность соответствующих значений функции сходится к числу A.

График функции, предел которой при аргументе, который стремится к бесконечности, равен L:

Предел функции по Гейне.

Значение А является пределом (предельным значением) функции f (x) в точке x₀ в случае, если для всякой последовательности точек , которая сходится к x₀, но которая не содержит x₀ как один из своих элементов (т.е. в проколотой окрестности x₀), последовательность значений функции сходится к A.

Предел функции по Коши.

Ответ

Необходимо рассчитать предел

Таким образом, числитель будет таким:

Далее сокращаем числитель и знаменатель на (x – 1):

Ответ

Решение пределов функции.

Чтобы решить пределы, следуйте правилам:

Разобравшись в сути и основных правилах решения предела, вы получите базовое понятие о том, как их решать.

Источник

Что означает предел в математике

Сага о погрешностях при участии слова lim

Кто о чём, а мы продолжаем разбирать сложную математику, чтобы она не была такой сложной.

Что такое предел в математике

Когда математики говорят о пределах, то имеют в виду такую последовательность событий:

Самое простое объяснение функции в математике.

👉 Стремиться — значит стараться приблизиться к какому-то числу, но не достигнуть его.

Если мы говорим, что переменная функции стремится к бесконечности, то это значит, что с каждым новым вычислением мы берём значение переменной больше предыдущего.

1, 2, 3, … 1000000000000003, 1000000000000004 и так до бесконечности

Наоборот тоже работает: если переменная функции стремится к нулю, то это значит, что она постоянно уменьшается:

1, 0.1, 0.01, 0.001, … 0.00000000000000000000000001 и с каждым разом число будет ближе к нулю, но никогда его не достигнет.

Стремление переменной к числу обозначается стрелкой: x→0, а предел — словом lim:

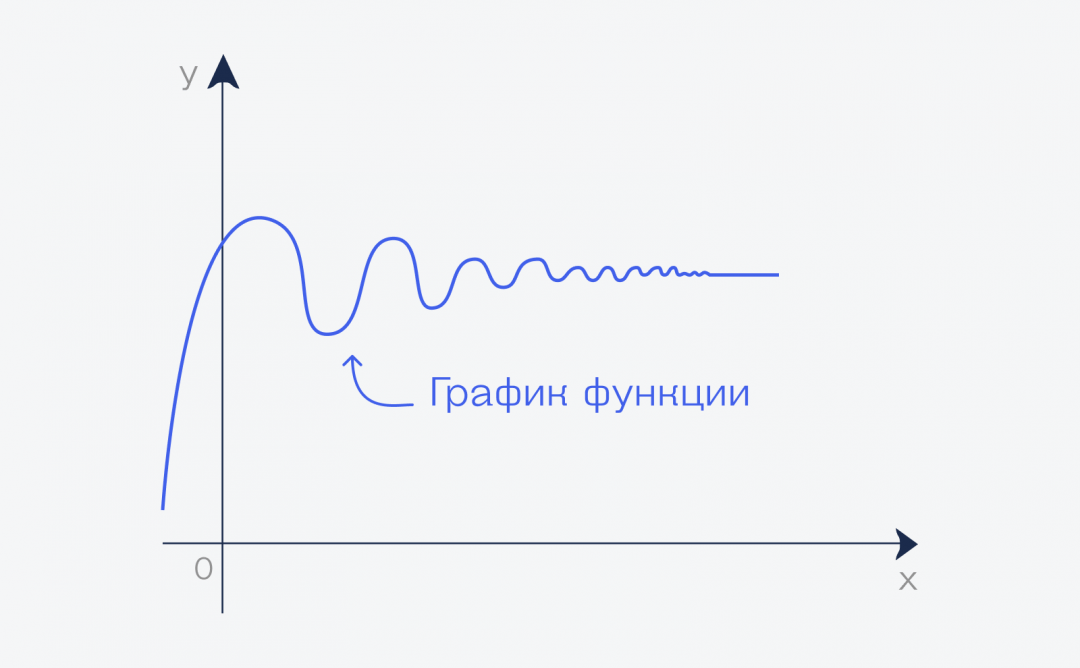
График и предел

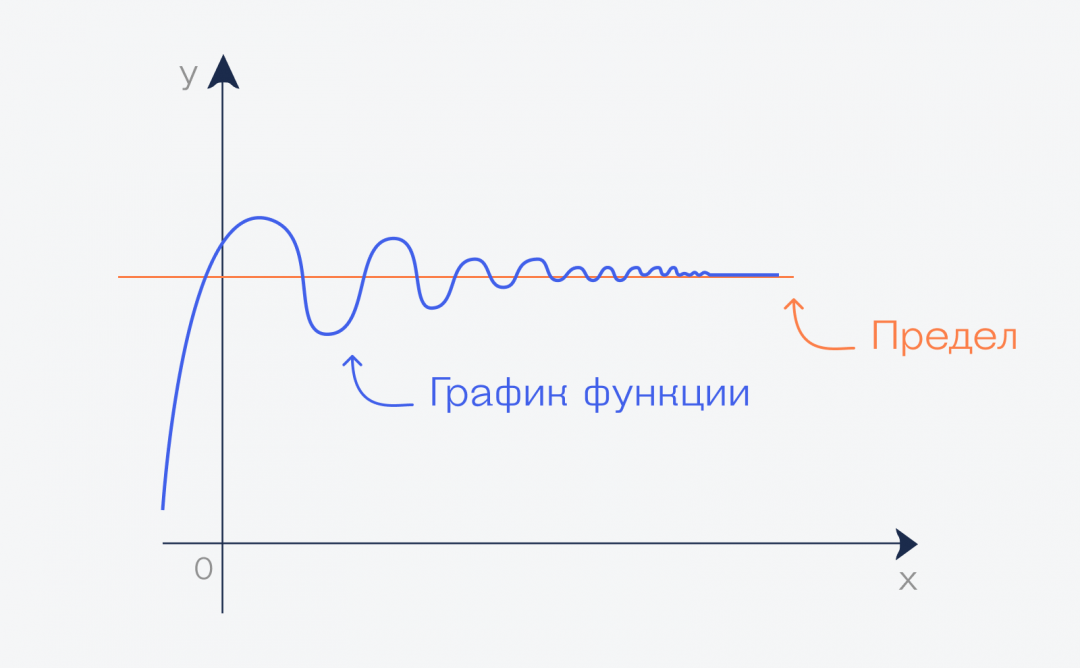
Если мы нарисуем график этой функции, то можем увидеть, что начиная с какого-то момента он превратится в почти прямую линию вдоль оси. Почти прямую — потому что прямой он никогда не станет, но стремится к этому, если продолжить рисовать график бесконечно.

Но бесконечный график означает, что у нас переменная функции стремится к бесконечности. А значение этой линии на графике — это и есть предел этой функции при переменной, стремящейся к бесконечности:

Пределы в жизни

Пределы из математики часто используются для решения практических задач, где нужно найти точку, после которой разница в результате будет уже незаметна.

Например, бригада монтажников строит мост, и им нужно понять, какой максимальной длины можно сделать плиту перекрытия. Есть требования, что плита должна выдерживать в середине нагрузку в 50 тонн — она может быть и прочнее, но 50 тонн это минимум. Для решения этой задачи используют предел — он покажет, длиннее какого размера делать плиту нельзя, а всё, что короче, даст необходимую прочность.

Астрономы с помощью пределов изучают законы Вселенной, физики проверяют всё на прочность, и даже в микроэлектронике затухание сигналов тоже зависит от пределов функций.

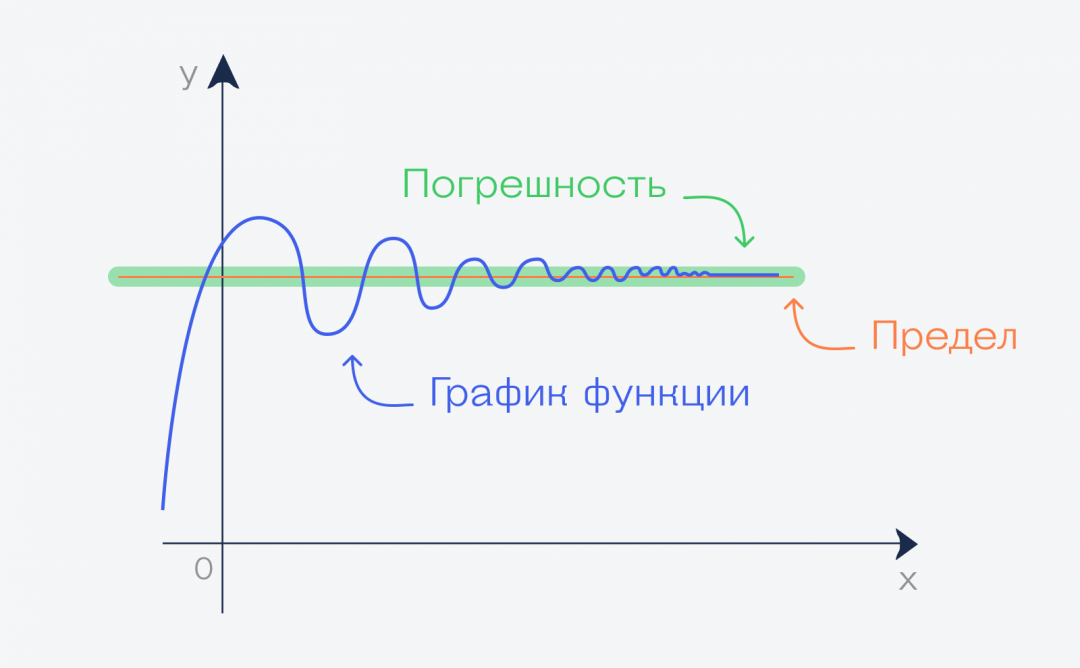
Погрешность в пределах

В математике пределы считаются точно: используются специальные формулы и трюки, которые помогают найти точный ответ. Но в жизни такая точность необязательна: можно взять любое решение, которое нас устроит с приемлемой погрешностью.

Эта погрешность поможет нам считать пределы, не зная точных математических формул подсчёта.

Считаем предел в программировании

Раз у нас есть постоянное действие по уменьшению или увеличению переменной, то логично сделать из этого простой цикл и поручить его машине. Единственное, что нам нужно предусмотреть, — момент, когда цикл должен остановиться, потому что в мире математики lim по умолчанию касается бесконечности (потому что стремиться можно бесконечно).

Так как мы не знаем заранее точного предела функции, но можем контролировать количество повторений, то сделаем такие условия для остановки цикла:

Самый сложный момент в коде — описать то, как переменная функции к чему-то стремится. Если к бесконечности, то всё просто: на каждом шаге прибавляем или умножаем на какое-то число. А если нужно, чтобы переменная стремилась к нулю или другому числу, то можно действовать так: брать начальное число, конечное, складывать их и делить пополам. Так мы будем постоянно приближаться к нужному нам числу, но никогда его не достигнем.

⚠️ Важная оговорка: числа в компьютере — это не числа в абстрактном математическом понимании, а конечный набор данных. Конечный он тем, что на всякое число выделяется какое-то количество «клеток», в которые это число можно записать. Если у нас ограниченное количество «клеток», значит, у нас есть какой-то предел самого большого и самого малого числа.

С точки зрения математики любое число можно бесконечно делить и получать бесконечное число знаков после запятой; а с точки зрения компьютера бесконечное число знаков невозможно, и если делить достаточно долго — мы получим ноль.

Поэтому в работе с пределами важно указывать либо число шагов для определения предела, либо погрешность.

Теперь напишем простой цикл, который нам посчитает lim x→2 (8−2x) / (x²−4x−12):

Если мы посчитаем этот предел как математики, то получим значение −1. Проверим, как с этим справится наш код:

Программа справилась и выдала результат с нужной нам точностью

Источник

Предел функции: основные понятия и определения

В этой статье мы расскажем, что из себя представляет предел функции. Сначала поясним общие моменты, которые очень важны для понимания сути этого явления.

Понятие предела

Если мы не можем определить ни конечное, ни бесконечное значение, это значит, что такого предела не существует. Примером этого случая может быть предел от синуса на бесконечности.

Что такое предел функции

В этом пункте мы объясним, как найти значение предела функции в точке и на бесконечности. Для этого нам нужно ввести основные определения и вспомнить, что такое числовые последовательности, а также их сходимость и расходимость.

При x → ∞ предел функции f ( x ) является бесконечным, если последовательность значений для любой бесконечно большой последовательности аргументов будет также бесконечно большой (положительной или отрицательной).

Решение

Далее мы запишем то же самое, но для бесконечно большой отрицательной последовательности.

Здесь тоже видно монотонное убывание к нулю, что подтверждает верность данного в условии равенства:

Ответ: Верность данного в условии равенства подтверждена.

Решение

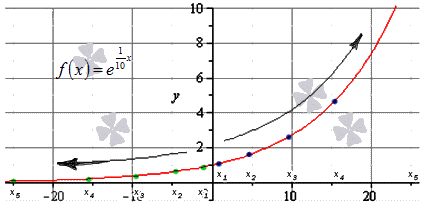
Мы видим, что данная последовательность бесконечно положительна, значит, f ( x ) = lim x → + ∞ e 1 10 x = + ∞

Наглядно решение задачи показано на иллюстрации. Синими точками отмечена последовательность положительных значений, зелеными ­ – отрицательных.

Перейдем к методу вычисления предела функции в точке. Для этого нам нужно знать, как правильно определить односторонний предел. Это пригодится нам и для того, чтобы найти вертикальные асимптоты графика функции.

Теперь сформулируем, что такое предел функции справа.

Теперь мы разъясним данные определения, записав решение конкретной задачи.

Решение

Значения функции в этой последовательности будут выглядеть так:

Чтобы более глубоко изучить теорию пределов, советуем вам прочесть статью о непрерывности функции в точке и основных видах точек разрыва.

Источник

Пределы в математике для чайников: объяснение, теория, примеры решений

Теория пределов – раздел математического анализа. Наряду с системами линейных уравнений и диффурами пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.

В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Понятие предела в математике

Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a, то a – предел этой величины.

Для определенной в некотором интервале функции f(x)=y пределом называется такое число A, к которому стремится функция при х, стремящемся к определенной точке а. Точка а принадлежит интервалу, на котором определена функция.

Звучит громоздко, но записывается очень просто:

Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.

Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:

Кстати, если Вас интересуют базовые операции над матрицами, читайте отдельную статью на эту тему.

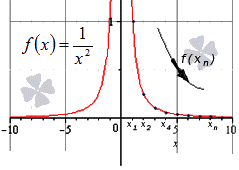
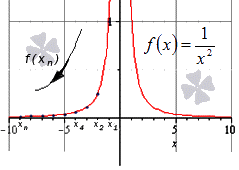
В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:

Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.

Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х. Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность. Что делать в таких случаях? Прибегать к хитростям!

Неопределенности в пределах

Неопределенность вида бесконечность/бесконечность

Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?

Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:

Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Еще один вид неопределенностей: 0/0

В таких случаях рекомендуется раскладывать числитель и знаменатель на множители. Но давайте посмотрим на конкретный пример. Нужно вычислить предел:

Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:

Сократим и получим:

Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.

Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:

Правило Лопиталя в пределах

Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?

Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.

Наглядно правило Лопиталя выглядит так:

Важный момент : предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.

А теперь – реальный пример:

Налицо типичная неопределенность 0/0. Возьмем производные от числителя и знаменателя:

Вуаля, неопределенность устранена быстро и элегантно.

Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос «как решать пределы в высшей математике». Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Что такое предел функции

В данной публикации мы рассмотрим одно из главных понятий математического анализа – предел функции: его определение, а также различные способы решения с практическими примерами.

Определение предела функции

Предел функции – величина, к которой стремится значение данной функции при стремлении ее аргумента к предельной для области определения точке.

Запись предела:

Таким образом, финальная запись предела выглядит выглядит так (в нашем случае):

Читается как “предел функции при икс, стремящемся к единице”.

x →1 – это значит, что “икс” последовательно принимает значения, которые бесконечно приближаются к единице, но никогда с ней не совпадут (ее не достигнут).

Решение пределов

С заданным числом

Давайте решим рассмотренный выше предел. Для этого просто подставляем единицу в функцию (т.к. x →1):

Таким образом, чтобы решить предел, сперва пробуем просто подставить заданное число в функцию под ним (если икс стремится к конкретному числу).

С бесконечностью

В данному случае аргумент функции бесконечно возрастает, то есть “икс” стремится к бесконечности (∞). Например:

Если x →∞, то заданная функция стремится к минус бесконечности (-∞), т.к.:

Другой более сложный пример

Для того, чтобы решить этот предел, также, просто увеличиваем значения x и смотрим на “поведение” функции при этом.

Таким образом при “икс”, стремящемся к бесконечности, функция неограниченно растет.

С неопределенностью (икс стремится к бесконечности)

В данном случае речь идет про пределы, когда функция – это дробь, числитель и знаменатель которой представляют собой многочлены. При этом “икс” стремится к бесконечности.

Пример: давайте вычислим предел ниже.

Выражения и в числителе, и а знаменателе стремятся к бесконечности. Можно предположить, что в таком случае решение будет таким:

Однако не все так просто. Чтобы решить предел нам нужно сделать следующее:

1. Находим x в старшей степени для числителя (в нашем случае – это два).

2. Аналогичным образом определяем x в старшей степени для знаменателя (тоже равняется двум).

3. Теперь делим и числитель, и знаменатель на x в старшей степени. В нашем случае в обоих случаях – во второй, но если бы они были разные, следовало бы взять наибольшую степень.

4. В получившемся результате все дроби стремятся к нулю, следовательно ответ равен 1/2.

С неопределенностью (икс стремится к конкретному числу)

И в числителе, и в знаменателе представлены многочлены, однако, “икс” стремится к конкретному числу, а не к бесконечности.

В данном случае условно закрываем глаза на то, что в знаменателе стоит ноль.

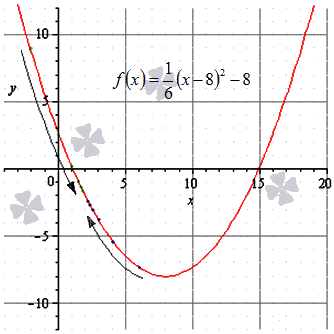
Пример: Найдем предел функции ниже.

1. Для начала подставим в функцию число 1, к которому стремится “икс”. Получаем неопределенность рассматриваемого нами вида.

2. Далее раскладываем числитель и знаменатель на множители. Для этого можно воспользоваться формулами сокращенного умножения, если они подходят, или решить квадратное уравнение.

Знаменатель () изначально является простым.

3. Получаем вот такой видоизмененный предел:

4. Дробь можно сократить на ():

5. Остается только подставить число 1 в выражение, получившееся под пределом:

Источник