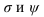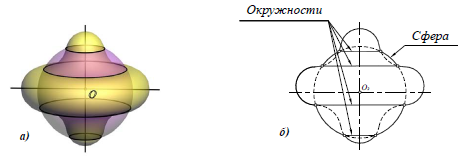Попарное соединение точек что это

Сколько точек пересечения могут иметь четыре попарно пересекающиеся прямые?

Сразу говорю, что задачу решать НЕ НАДО. Оставьте это мне. Я просто хочу разобраться, что означает «попарное пересекающиеся прямые».

У меня есть такая интерпретация: Имеется в виду, что все прямые «собраны» в пары. И каждая такая «сладкая парочка» пересекается другой такой же парой или «одиночной» прямой. Правда в этом конкретном случае «одиночек» нет, ибо количество прямых четное.

Я правильно все понимаю, или моя интерпретация неверна? Если неверна, то что тогда имеется в виду?

задан 23 Май ’13 13:26

I_Robot
183 ● 4 ● 17 ● 38
92&#037 принятых

Здесь имеется в виду, что какие бы две прямые из четырёх мы ни взяли, они будут пересекаться.

«они будут пересекаться.» Может быть, более точным будет сказать «они ДОЛЖНЫ пересекаться»?

Кстати, преобразуйте пожалуйста свой комментарий в ответ, дабы я мог закрыть вопрос.

3 ответа

Можно сказать «они пересекаются», «они должны пересекаться», «они будут пересекаться». Это всё одна и та же мысль. Суть в том, что любые две прямые из четырёх имеют точку пересечения. Фактически, это означает, что среди прямых нет параллельных (хотя в принципе такие прямые могли бы быть в какой-то другой ситуации, и тогда ответ был бы другим). Слово «попарно» вообще очень часто используется в математике. Например, «даны три попарно различных числа». Это значит, что первое число не равно второму, а также не равно третьему, а второе число не равно третьему.

отвечен 23 Май ’13 13:57

Если речь идет об одной паре прямых, то в одной точке, а ежели о двух парах и более, то рассматриваютя разные варианты расположения уже самих пересекающихся пар прямых.

отвечен 13 Сен ’15 13:02

Можете ли дать ссылку на определение «попарно пересекающиеся прямые» из учебника? Например как построить 5 попарно пересекающихся прямых? Можно-ли из этого сделать вывод, что одна прямая может пересекать лишь 2 других?

отвечен 22 Сен ’17 19:18

Здравствуйте

Источник

Попарное тестирование: суть техники, инструменты и примеры

Что такое попарное тестирование и почему оно является эффективной техникой тест-дизайна? Поговорим об этом ниже. Статья предназначена для начинающих специалистов по тестированию.

В этой статье пойдет речь о комбинаторной технике попарного тестирования (известной также как Pairwise testing или All-pairs testing).

Умное тестирование служит во благо экономии времени. Часто команда тестировщиков вынуждена работать в рамках жестких сроков 90% своего времени. По этой причине техники тест-дизайна должны быть эффективными, чтобы с их помощью можно было достичь максимально возможной степени покрытия тестами и вероятности обнаружения дефектов.

Что такое попарное тестирование?

Попарное тестирование — это техника тест-дизайна, которая обеспечивает полное тестовое покрытие.

ISTQB определяет попарное тестирование как технику тест-дизайна методом черного ящика, при которой тест-кейсы создаются таким образом, чтобы выполнить все возможные отдельные комбинации каждой пары входных параметров.

Результат работы приложения зависит от многих факторов, например, входных параметров, переменных состояний и конфигураций среды. Для определения возможных значений могут быть полезны такие техники, как анализ граничных значений и использование классов эквивалентности. Однако тестировать все возможные комбинации значений для всех факторов — непрактично. Поэтому, чтобы удовлетворить все факторы, генерируется подмножество комбинаций.

Техника попарного тестирования очень помогает при разработке тестов для приложений, включающих множество параметров. Тесты разрабатываются таким образом, что для каждой пары входных параметров существуют все возможные комбинации этих параметров. Тестовые наборы (тест-сьюты, Test suite) охватывают все комбинации. Поэтому техника хоть и не обеспечивает исчерпывающее тестирование, но все же является эффективной для поиска ошибок.

Давайте посмотрим, как применять технику попарного тестирования на примере.

Пример применения попарного тестирования

Приложение для заказа автомобиля:

С помощью приложения можно покупать и продавать машины. Приложение должно поддерживать оказание услуг в Дели и Мумбаи.

В приложении должны содержаться регистрационные номера, которые могут быть валидными и невалидным. Оно должно разрешать продажу следующих марок автомобилей: BMW, Audi и Mercedes.

Доступны два типа бронирования: бронирование через интернет и в офлайн-магазине.

Заказы доступны к размещению только в рабочие часы.

Шаг 1. Перечислим задействованные переменные.

Категория заказа
а. Купить
б. Продать

Местоположение
а. Дели
б. Мумбаи

Марка автомобиля
а. BMW
б. Audi
в. Mercedes

Регистрационные номера
а. Валидные (5000)
б. Невалидные

Тип заказа
а. Заказ через Интернет
б. Заказ в магазине

Время заказа
а. Рабочие часы
б. Нерабочие часы

Если тестировать все возможные допустимые комбинации: 2 X 2 X 3 X 5000 X 2 X 2 = получаем 240 тысяч комбинаций 🙁 Кроме того, недопустимых комбинаций вообще может быть бесконечное количество.

Шаг №2: Давайте упростим

Используем умную репрезентативную выборку.

Используем классы эквивалентности и граничные значения, даже если данные — непрерывные.

Сокращаем регистрационные номера до двух типов:

Валидный регистрационный номер

Невалидный регистрационный номер

Теперь посчитаем количество возможных комбинаций: = 2 X 2 X 3 X 2 X 2 X 2 = 96

Шаг 3. Упорядочивание задействованных переменных и значений.

Когда мы классифицируем задействованные переменные и значения, то получим что-то вроде этого:

Теперь отсортируем переменные так, чтобы переменные с наибольшим количеством значений шли первыми, а с наименьшим — последними.

Шаг 4. Расставляем переменные для создания набора тестов.

Давайте начнем заполнять таблицу столбец за столбцом. Изначально таблица выглядит примерно таким образом. Три значения в столбце «Марка авто» (переменная с наибольшим количеством значений) напишем дважды каждое (потому что следующая переменная, «Категория заказа», содержит два значения.

Столбец «Категория заказа» содержит два значения. И именно столько раз нам надо вставить значения первого столбца «Марка авто».

Для каждого набора значений в первом столбце мы помещаем оба значения второго столбца. Повторяем то же самое для третьего столбца.

Теперь у нас есть Покупка&Дели, но нет Покупка&Мумбаи. Есть Продажа&Мумбаи, но нет Продажа&Дели. Давайте поменяем значения из второго набора в третьем столбце.

Так уже выглядит получше.

Повторим шаги для столбцов 3 и 4.

Если сравнить столбцы 3 и 4, каждое значение из столбца 3 имеет пару с обоими значениями из столбца 4. Но если сравнить второй и четвертый столбец, у нас есть комбинации Покупка&Валидный и Продажа&Невалидный, но нет комбинаций Покупка&Невалидный и Продажа&Валидный. Следовательно, нам надо поменять местами последний набор значений в четвертом столбце.

С шестым столбцом (Время заказа) у нас проблемка: не хватает пар Покупка&Нерабочие часы и Продажа&Рабочие часы. Нам не удастся получить недостающие пары, поменяв значения местами, поскольку мы ранее уже поменяли местами все строки, и если мы снова начнём их менять, то есть риск пропустить другие возможные пары. Поэтому добавим еще два тестовых случая, которые содержат эти пары. Заполним пустые строки!

Теперь мы заполним пустые ячейки на свое усмотрение, потому что другие значения переменных являются произвольными (обозначим знаком тильды

Итого мы получили всего 8 тест-кейсов вместо 96.

Мы увидели, насколько эффективной может быть техника попарного тестирования. Она здорово повышает шансы найти баги, при этом сохранив время.

Однако эта техника имеет и некоторые ограничения. Она не сработает, если:

выбранные для тестирования значения некорректны;

мало внимания уделяется комбинациям, которые могут привести к ошибке с высокой долей вероятности;

взаимодействие между переменными недостаточно изучено.

Инструменты попарного тестирования:

Приведем примеры популярных инструментов, которые помогают эффективно автоматизировать процесс дизайна тест-кейсов путем создания компактного набора значений параметров в качестве желаемых тест-кейсов:

PICT – Попарное независимое комбинаторное тестирование от Microsoft Corp.

IBM FoCuS – Единое решение для функционального покрытия от IBM.

ACTS – Расширенная комбинаторная система тестирования от NIST, агентства правительства США.

VPTag – бесплатный инструмент попарного тестирования

Заключение:

Техника попарного тестирования помогает существенно уменьшить количество комбинаций проверок, достаточных для обеспечения необходимого уровня качества программного обеспечения. Это в самом деле умная техника тест-дизайна, которая гарантирует беспроигрышный результат как с точки зрения усилий и задействованных ресурсов, так и с точки зрения эффективности тестирования.

Об этой технике стоит помнить на этапе планирования тестирования. Независимо от того, генерируются ли тестовые случаи вручную или используется какой-либо вспомогательный инструмент, она становится необходимым компонентом тест-плана, потому что влияет на оценку тестирования.

Всех желающих приглашаем на бесплатное demo-занятие «Теория тестирования: виды тестирования». Чтобы быть хорошим специалистом, нужно понимать, какие виды тестирования бывают. На этом занятии мы:
— обсудим, по каким направлениям можно протестировать наш программный продукт;
— узнаем, что скрывается за белыми и черными ящиками;
— а также обсудим, чем отличаются стресс тесты от нагрузочных.

Источник

Взаимное пересечение поверхностей в начертательной геометрии с примерами

Содержание:

Взаимное пересечение поверхностей:

При пересечении поверхностей образуется линия, которую принято называть линией взаимного пересечения поверхностей. Эта линия пересечения принадлежит одновременно двум поверхностям. Поэтому построение линии пересечения сводится к определению точек одновременно принадлежащих обеим поверхностям. Для нахождения таких точек используется в общем случае метод вспомогательных секущих поверхностей. Сущность способа заключается в следующем: Пусть задано две поверхности

Общий алгоритм построения линии пересечения поверхностей:

В качестве посредников могут быть приняты как поверхности, так и плоскости, но целесообразно выбирать такие, которые дают наиболее простые линии пересечения с заданными поверхностями.

Взаимное пересечение поверхностей

Чтобы определить проекцию линии пересечения, необходимо найти проекции точек, общих для этих поверхностей. Их находят способом вспомогательных секущих плоскостей или вспомогательных сфер.

Если рёбра призмы или ось вращения цилиндра перпендикулярны какой-либо из плоскостей проекций, то на этой плоскости проекций линия пересечения совпадает с контуром основания призмы или цилиндра.

Пересечение двух многогранников

По чертежу видим, что только ребро DD’ пресекает поверхность пирамиды. Для определения точек пересечения 5 и б через ребро DD’ проводим горизонтальную плоскость, которая пересекает пирамиду по треугольнику. Точки 5 и 6 получаем, как пересечение DD’ с построенным треугольником.

Полученные точки соединяем с учетом видимости. Видимой считается тот отрезок прямой, который принадлежит двум видимым граням поверхностей.

Как видим, линия пересечения двух многогранников представляет собой пространственную ломаную линию.

Пересечение гранной и кривой поверхности

Линия пересечения гранной и кривой поверхности, представляет собой пространственную кривую линию, с точками излома на ребрах многогранника.

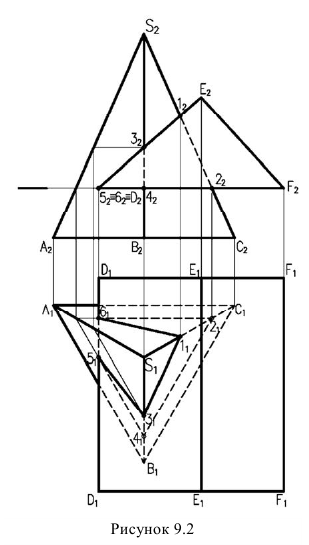
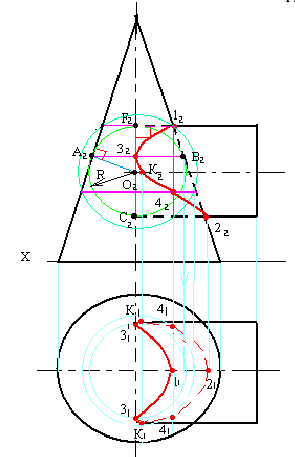
Поэтому сначала определяем точки пересечения ребер многогранника с кривой поверхностью, а затем промежуточные точки и соединяем их с учетом видимости. На рисунке 9.3 заданы поверхности трехгранной призмы и кругового конуса.

Так как призма фронтально-проецирующая, фронтальная проекция линии пересечения совпадает с проекцией боковых граней призмы, поэтому необходимо построить только горизонтальную проекцию линии пересечения.

Сначала определяем точки пересечения ребер призмы 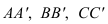с поверхностью конуса, а затем находим промежуточные точки, принадлежащие линиям пересечения. Для нахождения точек пересечения, используем горизонтальные плоскости посредники, так как они пересекают конус по окружностям, а призму но прямым линиям. Как видим, в данном случае линия пересечения распадается на две отдельные части.

Пересечение двух кривых поверхностей. Метод вспомогательных секущих плоскостей

Линия пересечения двух кривых поверхностей, представляет пространственную кривую линию. Поэтому для ее построения необходимо определить ряд точек принадлежащих этой лини.

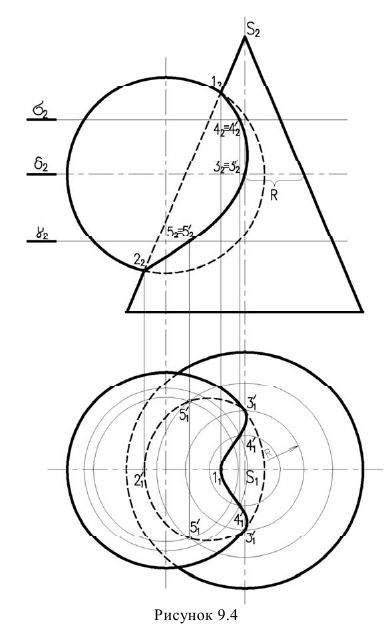
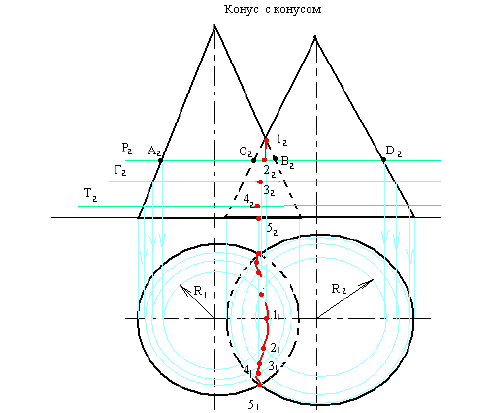
На рисунке 9.4 заданы поверхности конуса и сферы. Точки строятся при помощи горизонтальных плоскостей посредников, которые рассекают обе поверхности но окружностям.

Обязательно находим опорные точки, к которым относятся высшая и низшая точки линии пересечения и точки границы видимости. Так как оси поверхностей лежат в одной фронтальной плоскости, контурные образующие поверхностей пересекаются в точках 1 и 2 — это и будет высшая и низшая точки. Точки границы видимости лежат на экваторе сферы, поэтому точки 3 и 3′ находим с помощью вспомогательной горизонтальной плоскости, проходящей через центр сферы. Она рассекает сферу по экватору, а конус но параллели радиуса R.

Взаимно пересекаясь, они и дают точки 3 и 3′ фронтальную проекцию определяем по вертикальной линии связи на плоскости 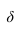Затем берем еще две вспомогательные плоскости расположенные выше и ниже плоскости и выполняя, аналогичные построения определяем точки 4 и 5 и 5′. Полученные точки соединяем с учетом видимости.

Пересечение поверхностей вращении. Метод вспомогательных секущих сфер

Способ вспомогательных секущих сфер применяется при следующих условиях:

Перед рассмотрением этого способа разберем понятие соосных поверхностей. Соосными называются поверхности вращения, имеющие общую ось. Соосные поверхности пересекаются по окружностям перпендикулярным оси вращения.

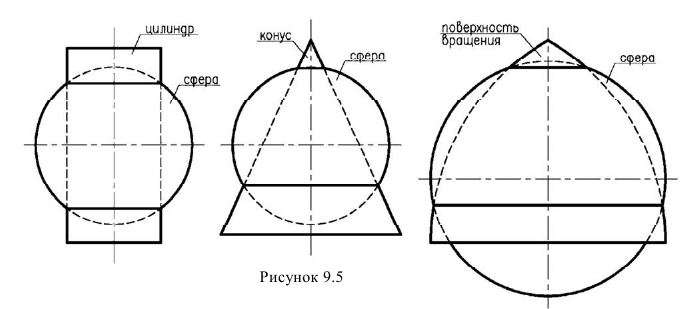
На рисунке 9.5 приведены некоторые из них.

Именно то, что поверхности пересекаются по окружностям, которые проецируются в линии и используется в методе сфер.

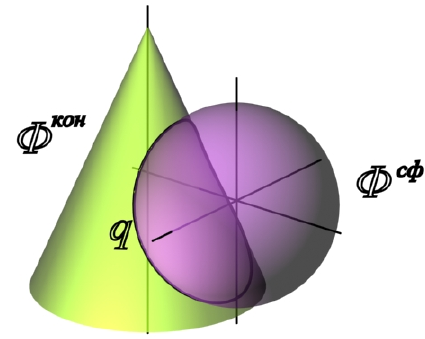
В данном случае минимальная сфера вписана в конус. Минимальная сфера касается поверхности конуса по окружности, а цилиндр пересекает по окружности. Нужно, иметь ввиду, что проекции окружностей пересечения перпендикулярны осям вращения. Эти две окружности пересекаются в точке . Фактически таких точек две, они совпадают на фронтальной проекции. Для построения промежуточных точек берем вспомогательные сферы радиусов в пределах от

Они пересекают и поверхность цилиндра, и поверхность конуса по окружностям, которые пересекаясь даюг промежуточные точки. Полученные точки соединяются плавной линией.

Здесь построена только фронтальная проекция. Для построения горизонтальной проекции, если это необходимо, точки строят как лежащие на окружностях полученных радиусов.

Теорема Монжа

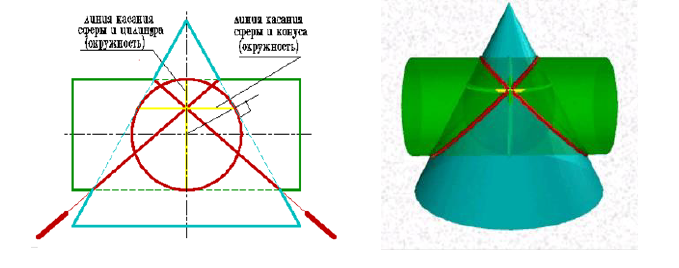
Рассмотрим вариант, когда минимальная сфера касается двух поверхностей вращения. В этом случае для построения линии пересечения поверхностей используется теорема Г. Монжа, которая формулируется так:

Если две поверхности вращении второго порядка описаны около третьей или вписаны в нее, то линии их пересечении распадается на две плоские кривые второго порядка. Плоскости этих кривых проходит через прямую, соединяющую точки пересечении линий касании.

Пересечение поверхностей вращения с многогранниками

Внешние и внутренние формы большинства предметов образуются сочетанием нескольких поверхностей. Пересекаясь между собой, они образуют линии, которые принято называть линиями перехода.

Рисунок 9.1 – Корпус с линиями перехода

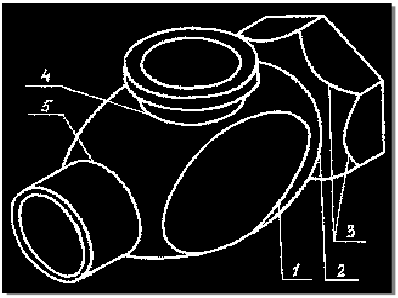
Линия пересечения многогранника с телом вращения в общем случае состоит из отдельных участков кривых линий, получающихся при пересечении граней многогранника с поверхностью вращения. Точки перехода от одного участка к другому находятся в пересечении ребер многогранника с телом вращения и называются точками излома. Участок линии пересечения может быть и прямой линией в случае пересечения линейчатой поверхности вращения гранью многогранника по образующей.

При проницании (полном пересечении) получаются две замкнутые линии пересечения. Они могут быть плоскими (поверхность вращения проницает одну грань) или пространственными, состоящими из нескольких плоских кривых с точками излома в местах пересечения поверхности вращения ребрами многогранника.

При врезании (неполном пересечении) получается одна замкнутая пространственная линия.

Таким образом, в соответствии с указанным выше, задачи данной темы решаются по следующему плану:

При построении точек линии пересечения многогранников с телами вращения используют вспомогательные секущие плоскости. Их располагают так, чтобы они пересекали данные поверхности по простым для построения линиям (прямым или окружностям).

Рассмотрим линии пересечения поверхности прямой трехгранной призмы с поверхностью конуса вращения. Боковые грани призмы являются фронтально-проецирующими плоскостями, а ось конуса перпендикулярна горизонтальной плоскости проекций.

Призму можно рассматривать, как три плоскости, проходящие через ее грани, а задача сводится к нахождению линий пересечения этих плоскостей с конусом.

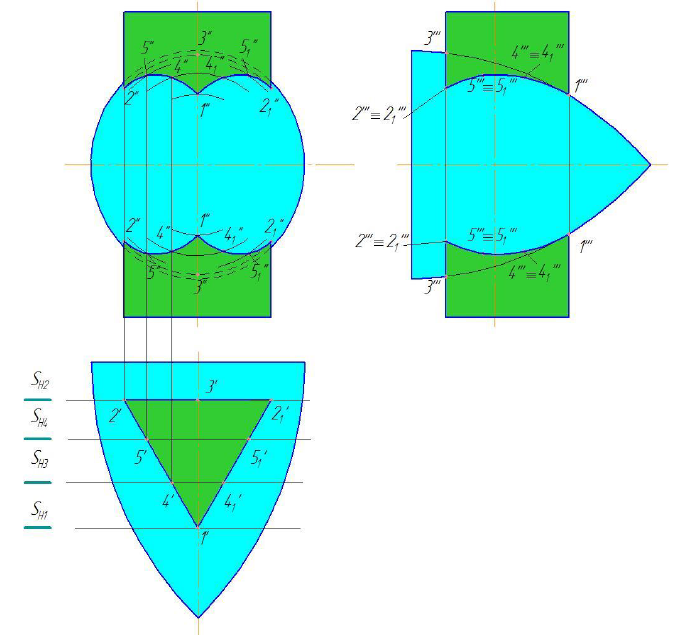
Пример. Построить линию пересечения поверхности тора с поверх-ностью трехгранной призмы (рис. 9.3).

Решение. Боковые грани призмы являются фронтально-проецирующими плоскостями и фронтальная проекция линии пересечения совпадают с проекцией боковой поверхности призмы. Из фронтальной проекции видно, что в данном случае имеет место проницание тора призмой (две замкнутые линии пересечения).

На рис. 9.3 рассмотрен пример пересечения поверхностей тора и треугольной призмы [2].

По двум заданным проекциям строим третью – профильную.

Рисунок 9.3 – Построение линии пересечения трехгранной призмы с тором

Заданная призма – горизонтально-проецирующая. Так как грани призматического отверстия перпендикулярны горизонтальной плоскости проекций, то на чертеже известна горизонтальная проекция линии пересечения, она совпадает с вырожденной проекцией поверхности призмы.

Следовательно, линия пересечения совпадает с горизонтальной проекцией основания призмы.

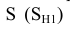
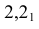
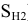
Определяем характерные точки: самую близкую точку 1 фронтальной плоскостью и самые далекие – и 3 фронтальной плоскостью S ().

Определяем промежуточные точки 4 и 5 при помощи вспомогательных фронтальных плоскостей .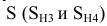

Соединяем полученные точки плавной кривой линией с учетом видимости.

Пересечение поверхностей вращения

Линия пересечения двух поверхностей вращения в общем случае представляет пространственную кривую, которая может распадаться на две и более части. Эти части могут быть, в частности, и плоскими кривыми и даже прямыми линиями.

Линию пересечения поверхностей обычно строят по ее отдельным точкам. Точки подразделяются на характерные (опорные) и промежуточные (случайные).

Общим способом построения этих точек является способ вспомогательных секущих поверхностей – посредников. При пересечении данных поверхностей вспомогательной поверхностью определяются линии пересечения ее с данными поверхностями, в пересечении этих линий получаются точки, принадлежащие искомой линии пересечения.

Наиболее часто в качестве поверхностей-посредников применяются плоскости или сферы.

Для определения линии пересечения часто пользуются вспомогательными секущими поверхностями. Поверхности-посредники пересекают данные поверхности по линиям, которые, в свою очередь, пересекаются в точках линии пересечения данных поверхностей.

Секущие поверхности-посредники выбираются так, чтобы они, пересекаясь с данными поверхностями, давали простые для построения линии, например прямые и окружности.

Способ вспомогательных секущих плоскостей

В качестве вспомогательных секущих плоскостей чаще всего используют плоскости, параллельные одной из плоскостей проекций.

Положение их выбирают таким, чтобы они пересекали заданные поверхности по простейшим линиям – прямым или окружностям.

Этот способ рекомендуется применять, если сечениями заданных поверхностей одной и той же плоскостью являются прямыми линиями или окружностями. Такая возможность существует в трех случаях:

Пересечение цилиндрической и торовой поверхности

Если одна из поверхностей является цилиндрической проецирующей поверхностью, то построение линии пересечения упрощается, так как в этом случае одна проекция линии пересечения совпадает с окружностью – проекцией цилиндра на перпендикулярную плоскость проекций.

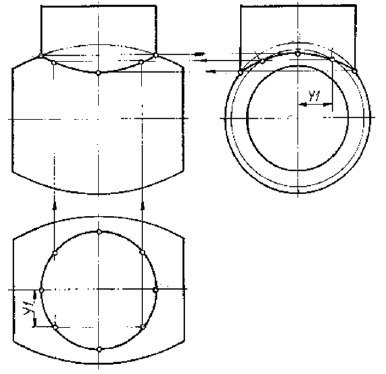
На рис. 9.4 построена линия перехода между цилиндром и тором. Так как поверхность цилиндра перпендикулярна плоскости Н, то горизонтальная проекция линии перехода известна. Она совпадает с горизонтальной проекцией цилиндра. Фронтальную и профильную проекции строим по принадлежности точек линии перехода не проецирующей поверхности тора.

Линия пересечения заданных поверхностей представляет собой пространственную кривую линию, имеющую фронтальную плоскость симметрии, образованную пересекающимися поверхностями цилиндра и тора.

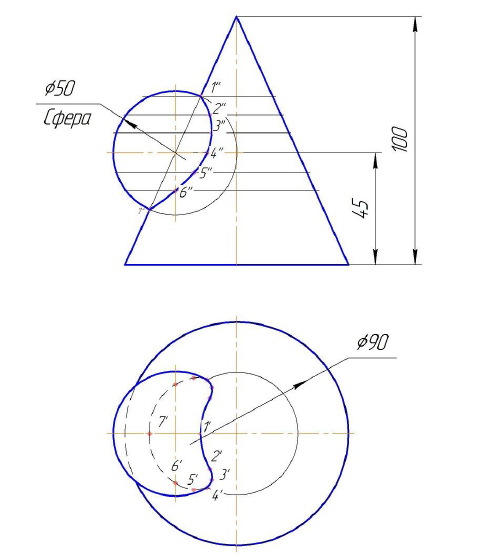
Рассмотрим линию пересечения поверхности сферы с поверхностью конуса вращения (Рисунок 9.5).

Точки 1 и 7, расположенные на очерках фронтальных проекций конуса и сферы, очевидны и определяются без дополнительных построений.

Точка 4 на экваторе сферы построена с помощью горизонтальной плоскости, пересекающей конус по окружности. В пересечении горизонтальных проекций этой окружности и экватора находится горизонтальная проекция 4′ точки 4 и фронтальная 4» проекции точки 4 определим с помощью линии связи. Точка 4 на горизонтальной проекции разделяет кривую на видимую и невидимую части.

Точки 2, 3, 5 и 6, расположенные в промежутке между характерными точками 1,4 и 7 строим аналогично. С помощью линий связи определим фронтальные и горизонтальные проекции этих точек.

Особые случаи пересечения

Пересечение соосных поверхностей вращения

Соосными называют поверхности вращения, оси которых совпадают. Линия пересечения таких поверхностей строится на основании теоремы о пересечении соосных поверхностей вращения: соосные поверхности вращения пересекаются между собой по окружностям.

Если ось вращения соосных поверхностей перпендикулярна к какой либо плоскости проекций, то линия их пересечения проецируется на эту плоскость в виде окружности, а на другую плоскость проекций – в прямую линию.

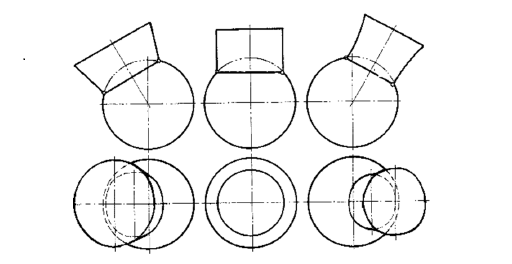
На рис. 9.6 даны примеры пересечения соосных поверхностей вращения (ось вращения параллельна горизонтальной плоскости). На рис. 9.6, а приведены сфера и конус, б – сфера и цилиндр, в – сфера и тор.

Теорема Монжа для пересекающихся поверхностей вращения

Если две поверхности второго порядка описаны около третьей или вписаны в нее, то линия их пересечения распадается на две плоские кривые второго порядка. Плоскости этих кривых проходят через прямую, соединяющую точки пересечения линий касания.

Для этого случая пересечения поверхностей вращения необходимо выполнение трех условий:

Это положение подтверждается теоремой Монжа: Если две поверхности второго порядка могут быть вписаны или описаны около третьей поверхности второго порядка, то пространственная кривая их пересечения четвертого порядка распадается на две плоские кривые второго порядка.

Способ вспомогательных секущих сфер

При построении линии пересечения поверхностей вращения не всегда удается подобрать секущие плоскости так, чтобы они пересекали поверхности по линиям, проекции которых были бы прямыми или окружностями. В некоторых таких случаях в качестве секущих поверхностей (посредников) целесообразно применять сферы. Этот способ основан на свойстве сферы пересекаться с любой поверхностью вращения, ось которой проходит через центр сферы по окружности.

Чтобы сфера одновременно пересекала две поверхности по окружностям, проецирующимся в прямые линии, необходимо выполнить условия:

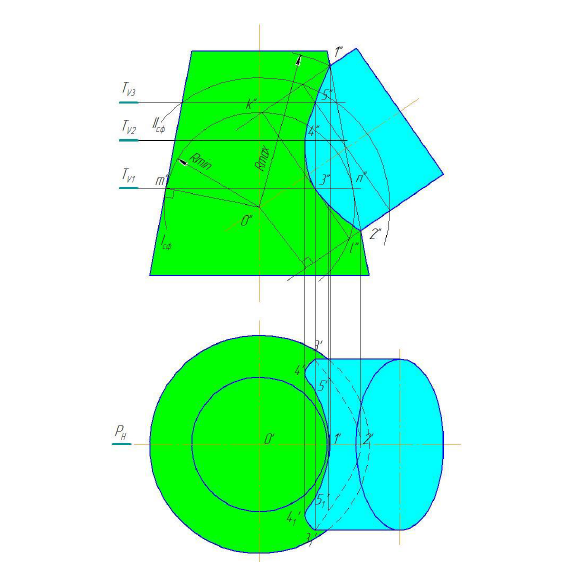
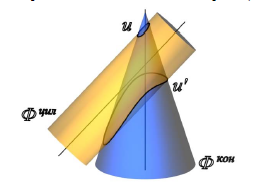
Пример. Построить проекции линии пересечения поверхностей конуса и цилиндра (рис. 9.8) [1].

Заданы прямой усеченный конус и наклонный цилиндр – тела вращения. Их оси параллельны фронтальной плоскости проекций и пересекаются в точке О(о′,о), т.е. соблюдены условия метода сфер.

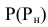
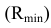
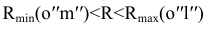
Как и в предыдущих задачах, найдем проекции характерных точек. Точка 1 – самая высокая, точка 2 – самая низкая. Чтобы убедится в этом проведем через оси тел вспомогательную фронтальную плоскость . Эта плоскость рассекает рассматриваемые тела по крайним очерковым образующим, которые на фронтальную плоскость проекции проецируются без искажения и, пересекаясь между собой, образуют искомые точки 1′, 2′. С помощью вспомогательных сфер найдем другие точки линии пересечения заданных поверхностей. Для определения радиуса наименьшей сферы из центра О(о′) проведем две нормали, перпендикулярные очерковым образующим этих тел и большей нормалью выполним эту сферу. Эта сфера будет наименьшей , проведенной в большем теле, поэтому поверхности конуса она касается по окружности, которая проецируется на фронтальную плоскость проекций в виде отрезка m′′n′′, а поверхность наклонного цилиндра пересекает по окружности, фронтальная проекция которой также проецируется в прямую линию k′′l′′. В пересечении k′′l′′ и m′′n′′ получим точку 3′′ – самую глубокую точку пересечения. Для нахождения промежуточных точек проведем ряд концентрических сфер, радиусы которых должны находится в пределе , и аналогично точке 3′′ находим необходимые промежуточные точки.

Учитывая, что сфера минимального радиуса всегда касается той поверхности, которая пронизывается другой, соединим найденные фронтальные проекции плавной кривой. Получим фронтальную проекцию линии пересечения. В нашем случае сфера радиусом 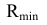касается поверхности конуса, значит, поверхность цилиндра пронизывает поверхность конуса.

Построим горизонтальную проекцию линии пересечения. Т.к. точки 1′′, 2′′ лежат на очерковой образующей конуса, то горизонтальные проекции этих точек находятся на оси конуса, т.е. на горизонтальной проекции этой образующей. Для нахождения горизонтальных проекций точек 3′, 4′, 5′ воспользуемся горизонтальными плоскостями 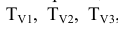, проведенными через эти точки соответственно. Каждая плоскость рассекает поверхность конуса по окружности, которая на горизонтальной плоскости проекций не искажается. По линиям связи найдем горизонтальные проекции точек 3′, 4′, 5′.

Для правильного соединения точек определим их видимость. Границей видимости на плоскости Н является точка 4′′, лежащая на осевой фронтальной проекции цилиндра. Горизонтальные проекции ее 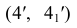находятся на очерковых образующих цилиндра. Соединив плавной кривой найденные точки, получим горизонтальную проекцию линии пересечения рассматриваемых тел.

Способ вспомогательных секущих плоскостей

Этот способ применим тогда, когда контуры отдельных сечений представляют прямые линии или окружности.

Проведём еще ряд горизонтальных секущих плоскостей и определим проекции других промежуточных точек линии пересечения, которые соединим лекальной кривой с учётом видимости.

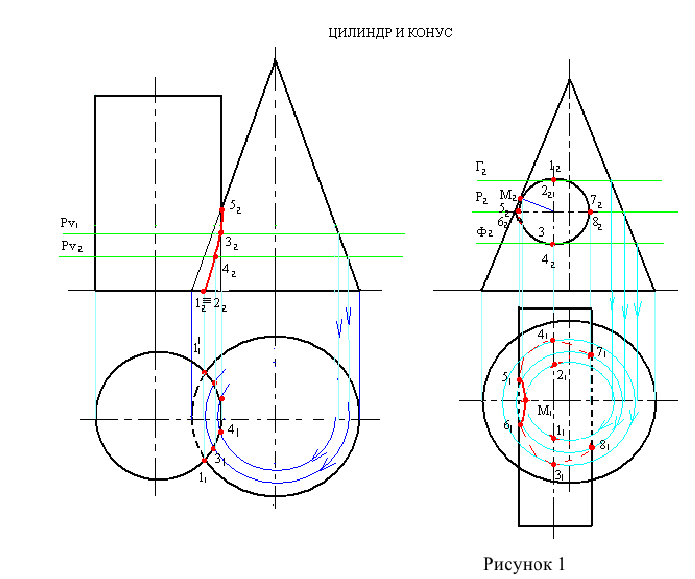
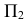
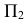
При взаимном пересечении конуса и цилиндра (рисунок 1) ось вращения цилиндра перпендикулярна . Значит, на линия пересечения совпадет с контуром основания цилиндра, т.е. фронтальной проекцией линии пересечения будет являться фронтальная проекция цилиндра.

Построив горизонтальную проекцию линии пересечения, на на пересечении горизонтальной оси симметрии цилиндра с проекцией цилиндра наметим точки — точки границы видимости линии пересечения, лежащие на экваторе цилиндра.

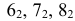
Способ вспомогательных сфер

Этот метод можно применять при соблюдении следующих условий :

Сфера 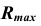проходит через самую дальнюю очевидную точку.

Сфера пересекает тела по окружностям, проецирующимся на одну из плоскостей проекций отрезком.

1. Определяем очевидные точки

1. Проводим ещё ряд секущих сфер радиусом больше минимальной и меньше максимальной и определяем другие промежуточные точки линии пересечения, которые соединяем лекальной кривой с учётом видимости.

Большее тело поглощает меньшее.

2. Видимость линии пересечения определяем следующим образом:

Элементы технического рисования

Обычно технический рисунок выполняется в изометрии.

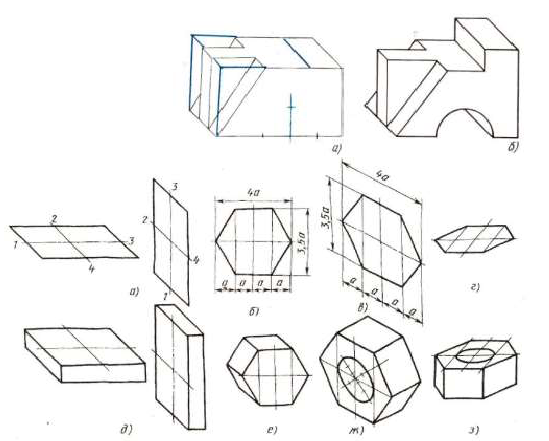
Технические рисунки получаются более наглядными, если их покрыть штрихами. При нанесении штрихов считают, что лучи света падают на предмет справа и сверху или слева и сверху.

Взаимное пересечение поверхностей с примерами

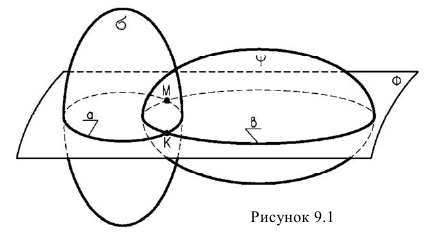
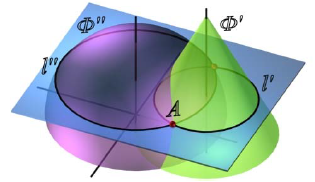
Алгоритм решения задач по определению линии пересечения поверхностей Ф’ и Ф» (рис. 9.1) в целом аналогичен решению второй позиционной задачи и состоит в следующем:

Рис. 9.1. Пересечение поверхностей

Определение точек линии пересечения поверхностей начинают с построения так называемых опорных точек. К ним относятся:

Способ вспомогательных параллельных плоскостей

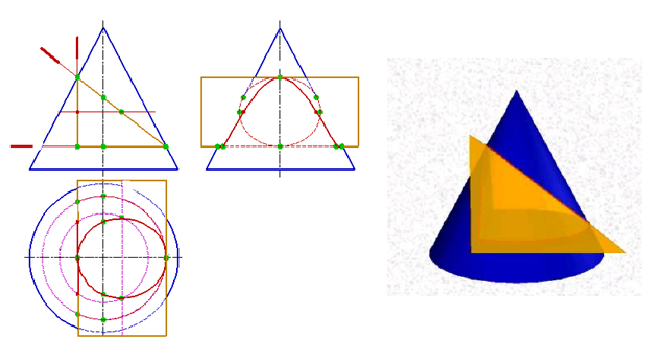
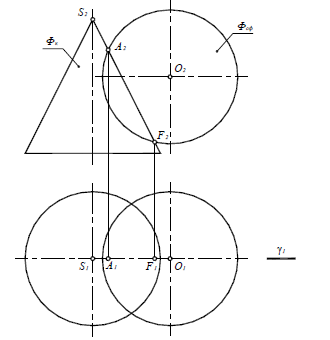
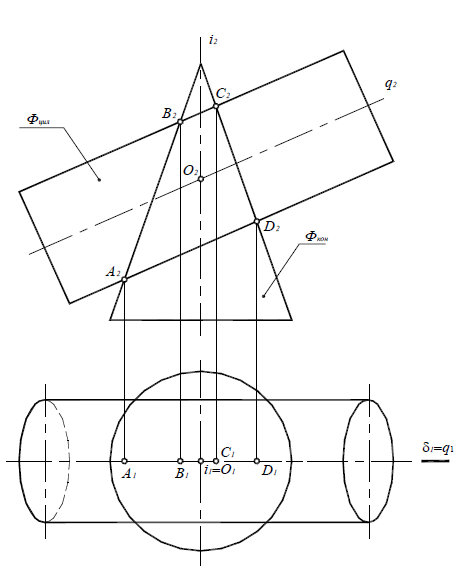
Рассмотрим построение линии пересечения прямого кругового конуса и сферы (рис. 9.2).

Рис. 9.2. Линия пересечения поверхностей прямого кругового конуса и сферы

Фронтальные плоскости уровня пересекают поверхность конуса по гиперболам, следовательно, для решения данной задачи нужно применить горизонтальные плоскости уровня, которые рассекают обе данные поверхности по окружностям.

Решение задачи начинают с построения опорных точек. Конус и сфера имеют общую плоскость симметрии γ(γ₁), параллельную плоскости П₂. Поэтому высшая точка A и низшая точка F линии пересечения получаются как результат пересечения очерковых образующих конуса и сферы (рис. 9.3).

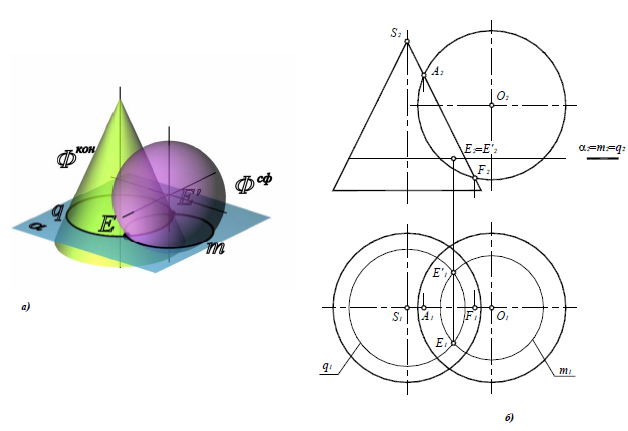
Остальные точки определяются с помощью горизонтальных плоскостей уровня. Более подробно разберем построение точек E и E'(рис. 9.4).

2. Построив горизонтальные проекции окружностей m и q, определить точки их пересечения E и E’:
E₁= m₁ × q₁; E₂=E₁E₂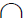α2.
E’₁=m₁ × q₁; E’₂=E_lE₂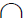α2.

Рис. 9.3. Определение опорных точек линии пересечения поверхностей

3. Аналогичным образом определяются остальные точки, формирующие линию пересечения (рис. 9.5,а). Они получены с помощью горизонтальных плоскостей уровня β(β₂), δ(δ₂) и μ(μ₂). Пределы этих плоскостей по высоте определяют высшая и низшая опорные точки линии пересечения поверхностей. Плоскость μ(μ₂)рассекает поверхность сферы по очерковой образующей b (b₂, b₂),поэтому полученные точки В и В’ являются опорными, ограничивающими линию пересечения поверхностей по ширине.

4. Последовательно соединить одноименные проекции полученных точек плавной лекальной кривой. Полученная линия не должна выходить за пределы области перекрытия проекций данных поверхностей.

5. Определить видимость линии пересечения поверхностей и их очерковых образующих.

Поверхность конуса на горизонтальной плоскости проекций полностью видима, следовательно, видимость линии пересечения определяется по поверхности сферы. Видима будет та часть сферы, которая на П₂ лежит выше очерковой образующей b₂.Точки В и В’ на очерковой образующей сферы являются точками смены видимости линии пересечения на плоскости проекций П₁.
Искомая линия пересечения поверхностей конуса и сферы d(d₁,d₂) (кривая второго порядка), полученная способом вспомогательных секущих плоскостей, приведена на рис 9.5,б.

Способ вспомогательных сфер

Способ концентрических сфер

Этот способ применяется для построения линии пересечения поверхностей вращения произвольного вида, при условии, что оси этих поверхностей пересекаются.

В основу способа концентрических сфер положено свойство сферы с центром на оси какой-либо поверхности.

Если центр сферы находится на оси любой поверхности вращения, то сфера соосна с поверхностью вращения и в их пересечении получатся окружности (рис. 9.6).

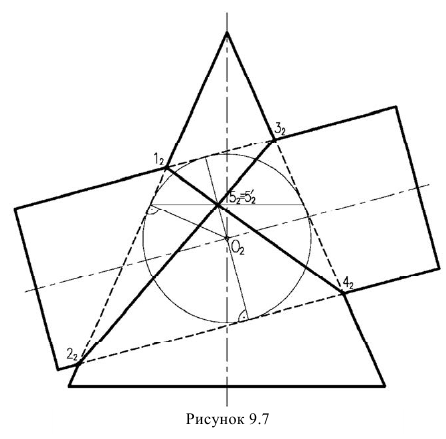
Рис. 9.7. Линия пересечения поверхностей цилиндра и прямого кругового конуса

Точка пересечения осей поверхностей принимается за центр вспомогательных концентрических сфер.

Алгоритм решения задачи об определении линии пересечения поверхностей состоит в следующем:

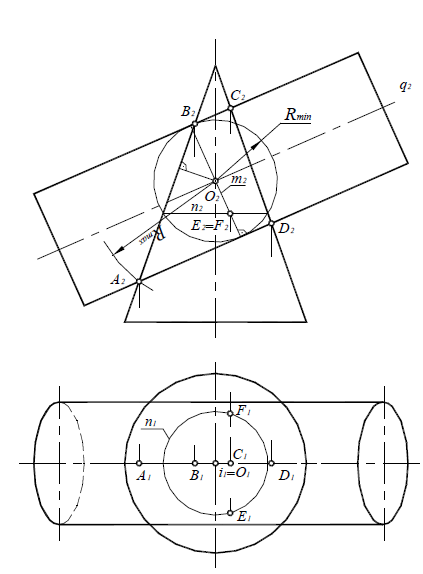
1. Определить опорные точки (рис. 9.8). Так как обе данные поверхности имеют общую плоскость симметрии δ(δ₁), параллельную плоскости проекций П₂, то их очерковые образующие, по отношению к плоскости П₂,пересекаются. Точки A(A₁,A₂), B(B₁,B₂), C(C₁,C₂) и D(D₁,D₂) пересечения этих образующих являются точками видимости линии пересечения поверхностей.

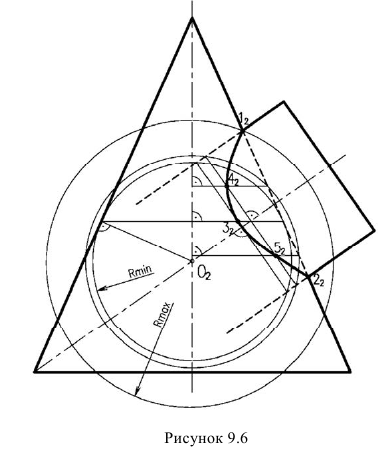
2. Определить радиусы максимальной и минимальной сфер, необходимых для определения точек линии пересечения.

Радиус максимальной сферы R_max равен расстоянию от центра вспомогательных сфер до наиболее удаленной точки пересечения очерковых образующих, в данном случае Rmax=O₂A₂ (рис. 9.9).

В данном случае сферой минимального радиуса является сфера, касающаяся цилиндрической поверхности (см. рис. 9.9).

Сфера радиусом R_min касается цилиндрической поверхности по окружности m, которая на фронтальной проекции изображается в виде прямой m₂, перпендикулярной q₂(m₂q₂). Эта же сфера пересекает коническую поверхность по двум окружностям. Но, в данном случае, нам интересна только окружность n, так как только она дает решение. Эта окружность n изображается на фронтальной проекции в виде прямой n₂, перпендикулярной i₂(n2i₂). Точки E и Fпересечения этих окружностей будут принадлежать обеим поверхностям:

Чтобы построить горизонтальные проекции точек Е и F следует воспользоваться окружностью n, содержащей данные точки, так как она не искажается на плоскости проекций П₁:

Рис. 108. Определение опорных точек линии пересечения поверхностей

Рис. 9.9. Определение радиусов максимальной и минимальной сфер.

Для построения промежуточных точек линии пересечения проводят несколько концентрических сфер с центром в точке O, причем радиус R этих сфер должен изменяться в пределах R_min

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник