Попарное пересечение прямых что это 5 класс
Упражнение 1
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Описание слайда:
Упражнение 1
Проведите прямые, проходящие через различные пары из данных точек. Сколько всего таких прямых?
Ответ: 6.
Описание слайда:
Упражнение 2
Проведите прямые, проходящие через различные пары из данных точек. Сколько всего таких прямых?
Ответ: 10.
Описание слайда:
Упражнение 3
Проведите прямые, проходящие через различные пары из данных точек. Сколько всего таких прямых?
Ответ: 10.
Описание слайда:
Упражнение 4
Сколько точек попарных пересечений могут иметь две прямые? Изобразите различные случаи.
Ответ: а) ни одной; б) одну.
Описание слайда:
Упражнение 5
Сколько точек попарных пересечений могут иметь три прямые? Изобразите различные случаи.
Ответ: 0, 1, 2, 3.
Описание слайда:
Упражнение 6
Изобразите четыре прямые так, чтобы у них было шесть точек попарных пересечений.
Ответ:
Описание слайда:
Упражнение 7
Изобразите пять прямых так, чтобы у них было десять точек попарных пересечений.
Ответ:
Описание слайда:
Упражнение 8
На сколько частей могут делить плоскость две прямые? Изобразите различные случаи.
Ответ: а) 3; б) 4.
Описание слайда:
Упражнение 9
На сколько частей могут делить плоскость три прямые? Изобразите различные случаи.
Ответ: а) 4; б) 6; в) 7.
Описание слайда:
Упражнение 10
На сколько частей разбивают плоскость прямые, изображенные на рисунке?
Ответ: 16.
Описание слайда:
Упражнение 11
Через точку C проведите прямую, параллельную прямой AB.
Ответ:
Описание слайда:
Упражнение 12
Через точку C проведите прямую, параллельную прямой AB.
Ответ:
Описание слайда:
Упражнение 13
Через точку C проведите прямую, параллельную прямой AB.
Ответ:
Описание слайда:
Упражнение 14
Через точку C проведите прямую, параллельную прямой AB.
Ответ:
Описание слайда:
Упражнение 15
Укажите пары параллельных прямых.
Ответ: a и f, b и e, c и g, d и h, p и q.
Описание слайда:
Упражнение 16
Через точку C проведите прямую, перпендикулярную прямой AB.
Ответ:
Описание слайда:
Упражнение 17
Через точку C проведите прямую, перпендикулярную прямой AB.
Ответ:
Описание слайда:
Упражнение 18
Через точку C проведите прямую, перпендикулярную прямой AB.
Ответ:
Описание слайда:
Упражнение 19
Через точку C проведите прямую, перпендикулярную прямой AB.
Ответ:
Описание слайда:
Упражнение 20
Укажите пары перпендикулярных прямых.
Ответ: a и r, b и g, b и c, c и e, e и g, f и r.
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Курс повышения квалификации
Охрана труда
Курс профессиональной переподготовки
Библиотечно-библиографические и информационные знания в педагогическом процессе
Курс профессиональной переподготовки
Охрана труда
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Похожие материалы
HDTV и 3DTV вещание через Интернет
ИНИСТ Банк Клиент Новое в генерации ключей
«Электричество и растения».
SMSDirect управляй рассылками легко!
Современное состояние страхового рынка, проблемы и инновационные пути развития
Оплата товаров и услуг без регистрации в системе WebMoney Transfer Через Терминалы оплаты.
Фармацевтические кластеры – мост через «долину смерти» для инновационных разработок
Не нашли то что искали?
Воспользуйтесь поиском по нашей базе из
5394315 материалов.
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Минпросвещения планирует выделить «Профессионалитет» в отдельный уровень образования
Время чтения: 2 минуты
Пик использования смартфонов приходится на 16 лет
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Рособрнадзор объявил сроки и формат ЕГЭ
Время чтения: 1 минута
В России утвердили новый порядок формирования федерального перечня учебников
Время чтения: 1 минута
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Сколько точек пересечения могут иметь четыре попарно пересекающиеся прямые?
Сразу говорю, что задачу решать НЕ НАДО. Оставьте это мне. Я просто хочу разобраться, что означает «попарное пересекающиеся прямые».
У меня есть такая интерпретация: Имеется в виду, что все прямые «собраны» в пары. И каждая такая «сладкая парочка» пересекается другой такой же парой или «одиночной» прямой. Правда в этом конкретном случае «одиночек» нет, ибо количество прямых четное.
Я правильно все понимаю, или моя интерпретация неверна? Если неверна, то что тогда имеется в виду?
задан 23 Май ’13 13:26
I_Robot
183 ● 4 ● 17 ● 38
92% принятых
Здесь имеется в виду, что какие бы две прямые из четырёх мы ни взяли, они будут пересекаться.
«они будут пересекаться.» Может быть, более точным будет сказать «они ДОЛЖНЫ пересекаться»?
Кстати, преобразуйте пожалуйста свой комментарий в ответ, дабы я мог закрыть вопрос.
3 ответа
Можно сказать «они пересекаются», «они должны пересекаться», «они будут пересекаться». Это всё одна и та же мысль. Суть в том, что любые две прямые из четырёх имеют точку пересечения. Фактически, это означает, что среди прямых нет параллельных (хотя в принципе такие прямые могли бы быть в какой-то другой ситуации, и тогда ответ был бы другим). Слово «попарно» вообще очень часто используется в математике. Например, «даны три попарно различных числа». Это значит, что первое число не равно второму, а также не равно третьему, а второе число не равно третьему.
отвечен 23 Май ’13 13:57
Если речь идет об одной паре прямых, то в одной точке, а ежели о двух парах и более, то рассматриваютя разные варианты расположения уже самих пересекающихся пар прямых.
отвечен 13 Сен ’15 13:02
Можете ли дать ссылку на определение «попарно пересекающиеся прямые» из учебника? Например как построить 5 попарно пересекающихся прямых? Можно-ли из этого сделать вывод, что одна прямая может пересекать лишь 2 других?
отвечен 22 Сен ’17 19:18
Здравствуйте
Пересечение прямых. Точка пересечения двух прямых
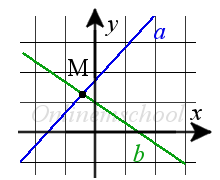
Если точка M, является точкой пересечения двух прямых, то она должна принадлежать этим прямым, а ее координаты удовлетворять уравнения этих прямых.
Точка пересечения двух прямых на плоскости
Если система уравнений:
Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
Вычтем из первого уравнения второе
Из первого уравнения найдем значение x
Подставим значение x во второе уравнение и найдем значение y
Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
В первое уравнение подставим значения x и y из второго и третьего уравнений.
Подставим значение t во второе и третье уравнение
Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
Из второго уравнения выразим y через x
Подставим y в первое уравнение
Решение: Обе прямые заданы уравнениями с угловым коэффициентом. Так как k 1 = k 2 = 2, то прямые параллельны. Так как эти прямые не совпадают то точек пересечения нет.
Решим также эту задачу используя систему уравнений:
Вычтем из первого уравнения второе
Ответ. Прямые не пересекаются (прямые параллельны).
Решение: Подставим координаты точки N в уравнения прямых.
Точка пересечения двух прямых в пространстве
Если система уравнений:
Решение: Составим систему уравнений
К шестому уравнению добавим пятое уравнение
Подставим значение b в четвертое и пятое уравнения
x = a + 1 y = a + 1 z = a + 1 a = 0 a = 0 b = 1 => x = 0 + 1 = 1 y = 0 + 1 = 1 z = 0 + 1 = 1 a = 0 a = 0 b = 1
Ответ. Прямые пересекаются в точке с координатами (1, 1, 1).
Решение: Составим систему уравнений заменив во втором уравнении параметр t на a
Подставим значение t из шестого уравнения в остальные уравнения
Какое наибольшее число прямых может получиться при попарных пересечениях?
Какое наибольшее число прямых может получиться при попарных пересечениях?
А) трёх плоскостей б) четырёх плоскостей * в) n плоскостей?
Непараллельные и не совпадающиеплоскости на пересечении образуют ровно одну прямую.
То же самое можно сказать про любую из N плоскостей, т.
Но надо понимать, что считая прямые таким образом, мы каждую прямую посчитали 2 раза, для первой плоскости и для второй, на пересечении которых она получилась, т.
Е. общее число прямых будет равно :
Для трех плоскостей получим число прямых = 3
На какое наибольшее число частей могут разделить плоскость 5 прямых?
На какое наибольшее число частей могут разделить плоскость 5 прямых?
Начертите три прересикающиеся прямые линии на плоскости?
Начертите три прересикающиеся прямые линии на плоскости.
На какое наибольшее число частей могут разбивать плоскость эти прямые.
На плоскости проведено пять попарно пересекающихся прямых?
На плоскости проведено пять попарно пересекающихся прямых.
Каким может оказаться наименьшее количество точек пересечения этих прямых?
На плоскости проведены три прямые?
На плоскости проведены три прямые.
Каким может оказаться наибольшее количество частей, на которые эти прямые разбили плоскость и каким наименьшее.
На плоскости проведено пять попарно пересекающихся прямых?
На плоскости проведено пять попарно пересекающихся прямых.
Каким может оказаться наименьшее количество точек пересечения этих прямых?
На плоскости проведено пять попарно пересекающихся прямых?
На плоскости проведено пять попарно пересекающихся прямых.
Каким может оказаться наименьшее колличество точек пересечения этих прямых?
Какое максимальное количество прямых углов может получится при проведении трёх прямых через одну точку на плоскости?
Какое максимальное количество прямых углов может получится при проведении трёх прямых через одну точку на плоскости?
На плоскости проведены четыре прямые какое наибольшее число точек пересечения могло получится?
На плоскости проведены четыре прямые какое наибольшее число точек пересечения могло получится.
Какое наибольшее число таких точек могло получится?