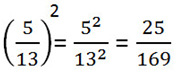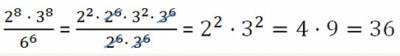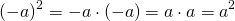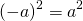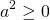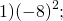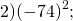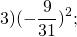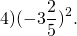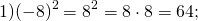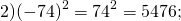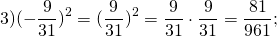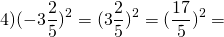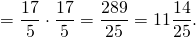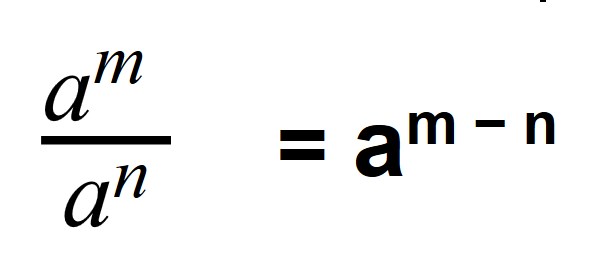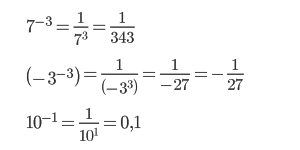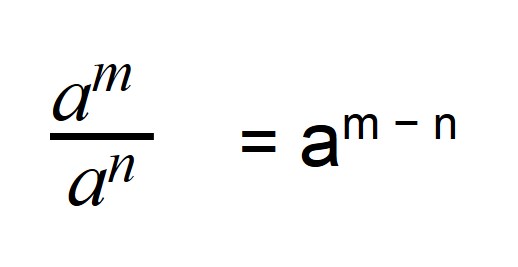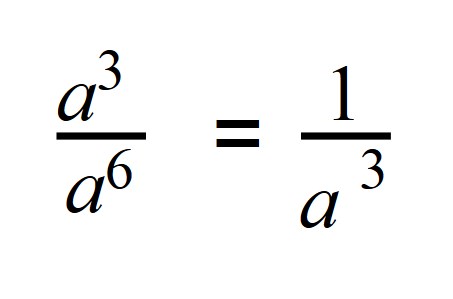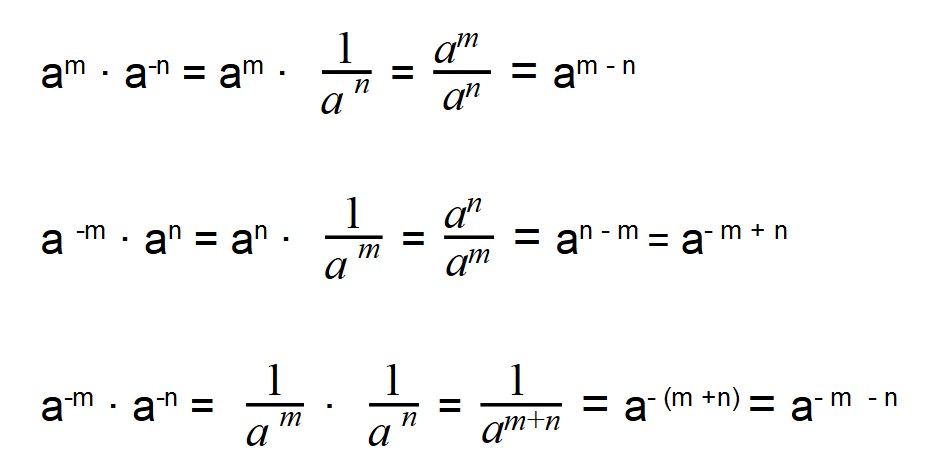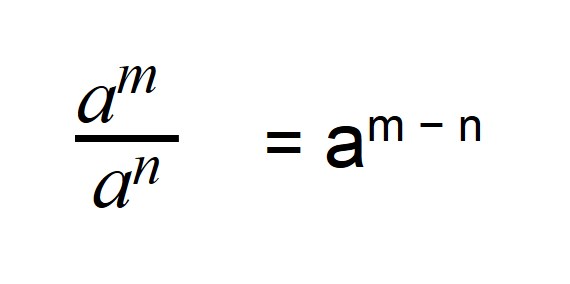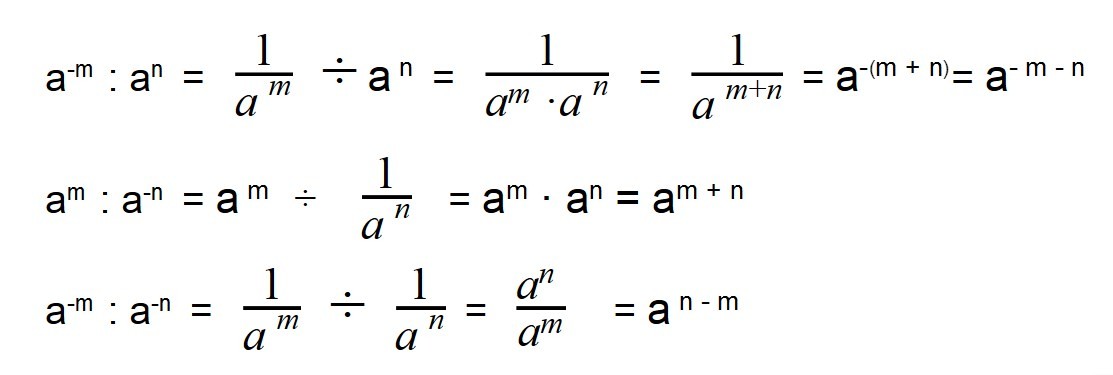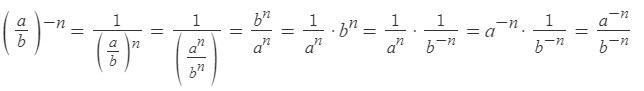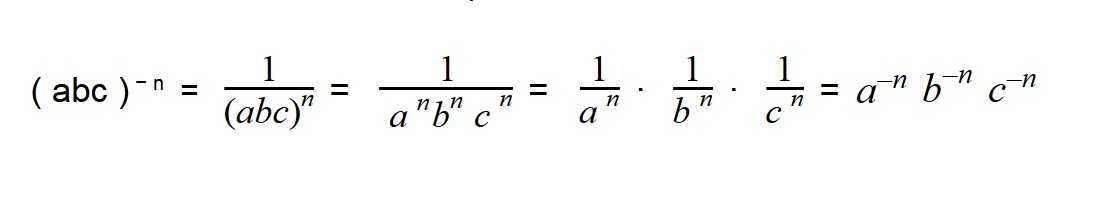Положительное число в квадрате равно чему
Урок 36 Бесплатно Умножение
В этом уроке мы узнаем, как перемножать два числа с разными знаками, а также разберемся, как перемножить два отрицательных числа.
Научимся возводить в квадрат как положительные, так и отрицательные числа, и предугадывать знаки результата умножения.
Также мы узнаем, как связаны между собой отрицательные числа и умножение на -1 и как это можно использовать.
Произведение чисел с разными знаками
Задача:
Кондитерская фабрика выпускает шоколадки по 3000 штук в день.
Фабрика изменила вес одной шоколадки на -10 грамм.
Вопрос: на сколько изменилось количество выпускаемого в день?
Для ответа на этот вопрос необходимо перемножить то, насколько меньше стал вес одной шоколадки, на общее количество шоколадок.
Так мы пришли к тому, что нам необходимо уметь перемножать числа с разными знаками.
Правило: чтобы перемножить числа с разными знаками, необходимо посчитать произведение модулей этих чисел и к результату приписать “минус”.
Применим это правило к нашей задаче:
2) Считаем произведение модулей:
3) Приписываем “минус” и получаем ответ: на -30000 грамм.
Как видите, все достаточно просто, приведем еще примеры:
Заметим, что произведение чисел с разными знаками всегда число отрицательное.
Так происходит потому, что сначала считается произведение модулей, поэтому произведение положительных чисел определенно будет положительным.
Далее мы приписываем к нему минус. А если приписать минус к положительному числу, то получится ни что иное, как число отрицательное.
Пройти тест и получить оценку можно после входа или регистрации
Произведение отрицательных чисел
Теперь посмотрим, что делать, если надо перемножить два отрицательных числа.
Правило: произведение двух отрицательных чисел равняется произведению их модулей.
Пример:
Необходимо перемножить \(\mathbf<-15>\) и \(\mathbf<-3>\)
1) Находим их модули:
2) Считаем произведение модулей:
Это и будет ответом.
Пример:
1) Посчитаем модули:
2) Считаем их произведение:
Ответ: \(\mathbf<\frac<1><4>>\)
И еще несколько примеров:
Заметим, что произведение отрицательных чисел всегда получается больше нуля.
Так происходит потому, что, по правилу, это произведение равняется произведению модулей этих чисел.
Все наши примеры это только подтверждают, что произведение отрицательных чисел получается положительным.
Пройти тест и получить оценку можно после входа или регистрации
Возведение числа в квадрат
Определение: квадратом числа а называется число \(\mathbf
Возможно, у вас уже возник вопрос, почему “квадрат”? Сразу ответим на него.
Чтобы найти площадь прямоугольника, необходимо перемножить длины двух его не противоположных сторон.
А у квадрата все стороны одинаковы, поэтому площадь равняется произведению стороны на саму себя, иными словами, площадь квадрата равняется квадрату длины его стороны.
Мы уже немного ушли в геометрию, которую вы будете изучать позже, а сейчас посмотрим на примеры нахождения квадратов.
Пример:
Найдем квадрат числа 3.
Считать будем по определению, перемножим 3 само на себя:
Еще пример на положительное число, найдем квадрат числа 12 :
Точно также нужно перемножить число само на себя:
И с нулем все также максимально просто: любое число при умножении на 0 дает 0, и сам 0 при умножении на 0 даст 0 :
Теперь посмотрим, что будет, если мы будем считать квадрат отрицательного числа:
Посчитаем квадрат \(\mathbf<-4>\):
Правило: квадрат отрицательного числа равен квадрату модуля отрицательных чисел.
Также заметим, что квадрат всегда неотрицателен.
Доказательство:
Таким образом, мы рассмотрели все возможные случаи, и во всех из них квадрат был числом неотрицательным, то есть положительным.
Пройти тест и получить оценку можно после входа или регистрации
Представление отрицательного числа как произведения
Мы уже знаем, что произведение отрицательного числа на положительное даст нам отрицательное число.
А что, если воспользоваться этим в обратную сторону?
Например, имеется отрицательное число \(\mathbf<-43>\)
Заметим, что оно равно \(\mathbf<-1\cdot43>\)
Также заметим, что квадрат от -1 равен 1.
Используя это в случаях с произведением чисел мы можем ловко менять и переставлять знаки.
Например, было такое произведение:
Преобразовав его можно оставить только один “минус”, смотрите:
Сейчас для больше наглядности мы переставим все -1 в начало, но этого можно и не делать:
Каждая пара минус единиц дает единицу. В данном случае минус единиц три штуки, значит, две из них дадут единицу, а третья останется:
Казалось бы, что нам это дало? А дало это нам то, что теперь знак выражения стал более наглядным: мы видим произведение -1 и произведение положительных чисел, являющегося положительным числом.
Вот теперь можно сказать, что ответом будет отрицательное число.
Правило: произведение нескольких чисел является отрицательным, тогда и только тогда, когда из его множителей нечетное количество является отрицательными и ни один множитель не равен нулю.
Оговорка про нуль важна, так как если один из множителей равен нулю, то и все выражение равно нулю, а значит, не является отрицательным.
Иногда -1 уходят полностью. Так происходят в случаях, когда отрицательных множителей четное число.
Пример:
Правило: произведение нескольких чисел является положительным тогда и только тогда, когда из его множителей их четное количество являются отрицательными и ни один множитель не равен нулю.
Отметим еще один момент: -1 можно выносить и заносить в обе стороны.
То есть в данном случае мы можем переписать выражение так:
Это же позволит превращать вычитание отрицательного числа в прибавление положительного. В самом деле:
Пройти тест и получить оценку можно после входа или регистрации
Дополнительная информация
Интересно посмотреть,как развивалась математика в Древней Руси.
В XVIII веке с приходом к власти Петра Первого (1672- 1725) в России появилась система образования, которая постепенно интегрировалась с общемировой и дала множество открытий.
Однако до этого момента тоже существовали математические познания, о которых мы сейчас и расскажем.
Как и в остальном мире, необходимость в математике была вызвана экономикой.
Поэтому одними из первых денежных знаков были домашние животные и шкуры.
Так, например, были резаны (куски шкур), куны (от слова “куница”) и ногаты.
Позже расчеты свели к гривнам: одна гривна, равная примерно 50-ти граммам серебра, равнялась 50-ти резанам, 25-ти кунам или 20-ти ногатам.
И уже позже, только к XIV веку, начали переходить к рублю, представлявшему из себя на тот момент круглый кусок серебра массой 205 грамм.
Меры длины во многих системах, в том числе и древнерусской, были связаны с параметрами человеческого тела:
Первый свод математических правил встречается в сборнике “Русская правда” (XI век), там опять же говорилось про экономику: штрафы, долги проценты, что лишний раз показывает, что люди уже умели оперировать целыми и дробными числами.
Далее выходили и другие труды, связанные с математикой, которые постепенно входили и в массы.
Книга “Считание удобное, которым всякий человек купующий или продающий, зело удобно изыскати может, число всякие вещи”, которая вышла в 1682 году, своим названием уже намекает на то, что предназначена была не только для ученых или любителей, но и для купечества.
Ну а дальше при Петре I появлялись школы, приглашались зарубежные специалисты, и наука шагнула далеко вперед.
По сей день российские ученые и студенты-математики выигрывают международные конкурсы и награды, решая нерешенные до этого задачи.
Заключительный тест
Пройти тест и получить оценку можно после входа или регистрации
Каталог статей
Степень числа
Итак, разберёмся, что такое степень числа. Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение. Так, вместо произведения шести одинаковых множителей 4 • 4 • 4 • 4 • 4 • 4 пишут 4 6 и произносят «четыре в шестой степени».
4 • 4 • 4 • 4 • 4 • 4 = 4 6

Запись a n читается так: «а в степени n» или «n-ая степень числа a».
Выражение 0 0 (ноль в нулевой степени) считают лишённым смыслом.
• (-32) 0 = 1
• 0 234 = 0
• 1 4 = 1
При решении примеров нужно помнить, что возведением в степень называется нахождение значения степени.
Пример. Возвести в степень.
• 5 3 = 5 • 5 • 5 = 125
• 2.5 2 = 2.5 • 2.5 = 6.25
• (3 ) 4 = 3• 3• 3• 3 = 81
4 4 4 4 4 256
При возведении нуля в натуральную степень получается ноль.
При возведении в степень отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.
Рассмотрим примеры возведения в степень отрицательных чисел. 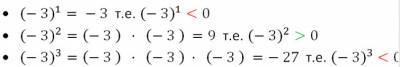
Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень, то получается отрицательное число. Так как произведение нечётного количество отрицательных сомножителей отрицательно.
Если же отрицательное число возводится в чётную степень, то получается положительное число. Так как произведение чётного количество отрицательных сомножителей положительно.
Отрицательное число, возведённое в чётную степень, есть число положительное.
Вычислить (- 5) 4 означает найти значение четвёртой степени отрицательного числа.
(- 5) 4 = (- 5) • (- 5) • (- 5) • (- 5) = 625
Порядок действий в примерах со степенями
Вычисление значения называется действием возведения в степень. Это действие третьей ступени.
Cвойства степени
Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.
Свойство № 1
Произведение степеней
Данное свойство степеней также действует на произведение трёх и более степеней.
Примеры.
• Упростить выражение.
b • b 2 • b 3 • b 4 • b 5 = b 1+2+3+4+5 = b 15
• Представить в виде степени.
6 15 • 36 = 6 15 • 6 2 = 6 15+2 = 6 17
• Представить в виде степени.
(0,8) 3 • (0,8) 12 = (0,8) 3+12 = (0,8) 15
Свойство № 2
Частное степеней
Примеры.
• Записать частное в виде степени
(2b) 5 : (2b) 3 = (2b) 5-3 = (2b) 2
• Пример. Решить уравнение. Используем свойство частного степеней.
3 8 : t = 3 4
Свойство № 3
Возведение степени в степень
• Пример.
(a 4 ) 6 = a 4 • 6 = a 24
• Пример. Представить 3 20 в виде степени с основанием 32.
По свойству возведения степени в степень известно, что при возведении в степень показатели перемножаются, значит:
Свойства 4
Степень произведения
(6 • a 2 • b 3 • c ) 2 = 6 2 • a 2 • 2 • b 3 • 2 • с 1 • 2 = 36 a 4 • b 6 • с 2
(- x 2 • y) 6 = ( (- 1) 6 • x 2 • 6 • y 1 • 6 ) = x 12 • y 6
Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке.
(a n • b n )= (a • b) n
То есть, чтобы перемножить степени с одинаковыми показателями можно перемножить основания, а показатель степени оставить неизменным.
• Пример. Вычислить.
2 4 • 5 4 = (2 • 5) 4 = 10 4 = 10 000
0,5 16 • 2 16 = (0,5 • 2) 16 = 1
В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. В этом случае советуем поступать следующим образом.
Например, 4 5 • 3 2 = 4 3 • 4 2 • 3 2 = 4 3 • (4 • 3) 2 = 64 • 12 2 = 64 • 144 = 9216
Пример возведения в степень десятичной дроби.
4 21 • (-0,25) 20 = 4 • 4 20 • (-0,25) 20 = 4 • (4 • (-0,25)) 20 = 4 • (- 1) 20 = 4 • 1 = 4
Свойства 5
Степень частного (дроби)
• Пример. Представить выражение в виде частного степеней.
(5 : 3) 12 = 5 12 : 3 12
Возведение в степень дроби
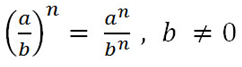
Примеры возведения в степень дроби.
Как возвести в степень смешанное число
Чтобы возвести в степень смешанное число, сначала избавляемся от целой части, превращая смешанное число в неправильную дробь. После этого возводим в степень и числитель, и знаменатель.
Пример.
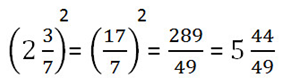
Формулу возведения в степень дроби применяют как слева направо, так и справа налево, то есть, чтобы разделить друг на друга степени одинаковыми показателями, можно разделить одно основание на другое, а показатель степени оставить неизменным.
• Пример. Найти значение выражения рациональным способом.
Квадрат отрицательного числа
Как найти квадрат отрицательного числа? Что можно сказать о значении квадрата любого числа?
Чтобы найти квадрат числа, надо это число взять множителем два раза.
Соответственно, чтобы возвести в квадрат отрицательное число, надо найти произведение двух множителей, каждый из которых равен этому отрицательному числу.
При умножении отрицательных чисел получаем положительное число. Значит, знак «минус» при возведении в квадрат отрицательного числа уходит:
Следовательно, квадрат отрицательного числа равен квадрату противоположному ему числа:
Таким образом, значение квадрата любого отрицательного числа равно положительному числу.
Квадрат положительного числа является числом положительным.
Квадрат нуля равен нулю.
Вывод: квадрат любого числа является неотрицательным числом:
Чтобы возвести в квадрат отрицательное число, можно возвести в квадрат противоположное ему число (знак «-» не писать).
Найти квадрат отрицательного числа:
(При вычислении квадратов можно пользоваться готовыми значениями).
(Найти квадрат дроби можно одним из двух способов).
2 Comments
Свойства степеней. Действия со степенями
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Что такое степень числа
В учебниках по математике можно встретить такое определение:
«Степенью n числа а является произведение множителей величиной а n раз подряд»
a — основание степени;
n — показатель степени.
Читается такое выражение, как a в степени n
Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) само на себя.
А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:
2 — основание степени;
3 — показатель степени.
Если вам нужно быстро возвести число в степень, можно использовать наш онлайн-калькулятор. Но чтобы не упасть в грязь лицом на контрольной по математике, придется все-таки разобраться с теорией.
Рассмотрим пример из жизни, чтобы было понятно, для чего можно использовать возведение чисел в степень на практике.
Задачка про миллион: представьте, что у вас есть миллион рублей. В начале каждого года вы зарабатываете на нем еще два. Получается, что миллион каждый год утраивается. Был один, а стало три — и так каждый год. Здорово, правда? А теперь посчитаем, какая сумма у вас будет через 4 года.
Как решаем: один миллион умножаем на три (1·3), затем результат умножаем на три, потом еще на три. Наверное, вам уже стало стало скучно, потому что вы поняли, что три нужно умножить само на себя четыре раза. Так и сделаем:
Математики заскучали и решили все упростить:
Ответ: через четыре года у вас будет 81 миллион.
Таблица степеней
Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).
Отрицательная степень
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Что такое степень числа
В учебниках по математике можно встретить такое определение:
«Степенью n числа а является произведение множителей величиной а n раз подряд»
Например, a n — степень, где:
Читается такое выражение как a в степени n.
Если говорить проще, то степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить данное число (основание степени) само на себя.
А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:
Таблица степеней
Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).
Свойства степеней
Степень с натуральным показателем в математике имеет несколько важных свойств, которые позволяют упрощать вычисления. Всего их пять штук — ниже мы их рассмотрим.
Свойство 1: произведение степеней
При умножении степеней с одинаковыми основаниями, основание мы оставляем без изменений, а показатели степеней складываем:
Свойство 2: частное степеней
Когда мы делим степени с одинаковыми основаниями, то основание остается без изменений, а из показателя степени делимого вычитают показатель степени делителя.
Свойство 3: возведение степени в квадрат
Когда возводим степень в степень, то основание степени остается неизмененным, а показатели степеней умножаются друг на друга.
Свойство 4: степень произведения
При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.
Свойство 5: степень частного
Чтобы возвести в степень частное, можно возвести в эту степень сначала делимое, потом делитель, и первый результат разделить на второй.
Степень с показателем 0
Любое целое a ≠ 0 в степени 0 равно 1.
Выражение 0 в степени 0 многие математики считают лишенным смысла, так график функции f (x, у) = xy прерывается в точке (0; 0).
Степень с отрицательным показателем
Число в минусовой степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем:
Чтобы разобраться, как возводить число в отрицательную степень, вспомним правило деления степеней с одинаковыми основаниями.
Деление степеней с одинаковыми основаниями, но разными показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.
Поэтому если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:
Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:
Действия с отрицательными степенями
Умножение отрицательных степеней
При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются, так же как и при умножении положительных степеней:
Деление отрицательных степеней
При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя, так же как и при делении положительных степеней:
Возведение дроби в отрицательную степень
Чтобы возвести дробь в отрицательную степень, надо возвести в эту степень отдельно числитель и знаменатель:
Возведение произведения в отрицательную степень
Чтобы возвести произведение в отрицательную степень, необходимо возвести в эту степень каждый множитель произведения отдельно: