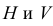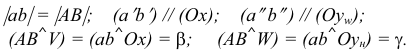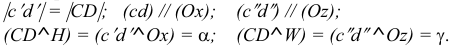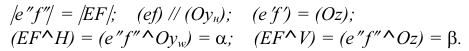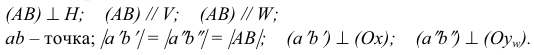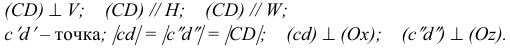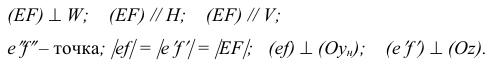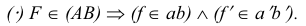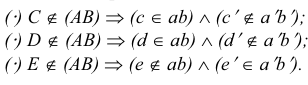Показать что точки лежат на одной прямой

Показать что точки лежат на одной прямой

Если три точки A, B и C лежат на одной прямой, то треугольник ABC обратится в отрезок прямой, а потому его площадь должна быть равна нулю. Полагая в формуле

S = 0, получим условие, при котором три точки лежат на одной прямой

В более удобной форме условие, при котором три точки лежат на одной прямой, можно записать так:

(1)

Подставляя сюда координаты данных точек, получим, что левая часть (1) будет равна

Требование (1) выполнено:

и, значит, три данные точки лежат на одной прямой.

Источник

Вычислительная геометрия, или как я стал заниматься олимпиадным программированием. Часть 2

Вступление

Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.

Начнем с взаимного расположения точки относительно прямой, луча и отрезка.

Задача №1

Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.

Решение
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P₁(x₁, y₁), P₂(x₂, y₂). В этом случае можно спокойно найти коэффициенты a, b и c и применить предыдущее рассуждение. Но надо сначала подумать, оно нам надо? Конечно, нет! Как я говорил косое произведения — это просто жемчужина вычислительной геометрии. Давайте применим его. Известно, что косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому нам достаточно посчитать косое произведение векторов P₁P₂ и P₁M и по его знаку сделать вывод.

Задача №2

Определить принадлежит ли точка лучу.

Решение
Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P₁(x₁, y₁) — начало луча, а P₂(x₂, y₂) — любая точка принадлежащая лучу. Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P₁(x₁, y₁), где P₂(x₂, y₂) лежит на луче необходимо и достаточно выполнения двух условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (P₁P₂, P₁M) ≥ 0 – скалярное произведение (точка лежит на луче)

Задача №3

Определить принадлежит ли точка отрезку.

Решение
Пусть точки P₁(x₁, y₁), P₂(x₂, y₂) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P₁, P₂. Далее нам нужно определить лежит ли точка между точками P₁ и P₂, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP₁, MP₂). Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка. Почему так? Посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P₁(x₁, y₁), P₂(x₂, y₂) необходимо и достаточно выполнения условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (MP₁,MP₂) ≤ 0 – скалярное произведение (точка лежит между P₁ и P₂)

Задача №4

Взаимное расположение двух точек относительно прямой.

Решение
В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.

Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.
Итак:
1. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] 0 – точки лежат по одну сторону.
3. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] = 0 – одна (или две) из точек лежит на прямой.

Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также. Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] ≤ 0.

Задача №5

Определить пересекаются ли две прямые.

Решение
Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.
Допустим прямые заданы своими уравнениями a₁x + b₁y + c₁ = 0 и a₂x + b₂y + c₂ = 0. Тогда условие параллельности прямых заключается в том, что a₁b₂ — a₂b₁ = 0.
Если же прямые заданы точками P₁(x₁, y₁), P₂(x₂, y₂), M₁(x₃, y₃), M₂(x₄, y₄), то условие их параллельности заключается в проверки косого произведения векторов P₁P₂ и M₁M₂: если оно равно нулю, то прямые параллельны.

В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b₁, a₁), (-b₂, a₂) которые называются направляющими векторами.

Задача №6

Определить пересекаются ли два отрезка.

Решение
Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:

Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P₁P₂, P₁M₂] > 0, [P₁P₂, P₁M₁] [P₁P₂, P₁M₂] * [P₁P₂, P₁M₁] 2 + b 2 ).

Задача №8

Расстояние от точки до луча.

Решение
Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.

В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.

Теперь рассмотрим случай, когда центр второго круга O₂ находится между точками O₁ и C. В этом случае получим отрицательное значение величины d₂. Использование отрицательного значения d₂ приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.

Заключение

Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.

Источник

Теорема Менелая, теорема Чевы – нужны на ЕГЭ или нет?

Разберемся, что это за теоремы и как применяются. И действительно ли на ЕГЭ дали задачи на применение теорем, выходящих за рамки школьной программы. И можно ли эти задачи решить по-другому?

Теорема Менелая:

Пусть прямая пересекает произвольный треугольник причем – точка ее пересечения со стороной – точка ее пересечения со стороной и – точка ее пересечения с продолжением стороны

Тогда выполняется равенство:

Как это запомнить? Сначала рисуем треугольник Затем прямую, пересекающую две его стороны и продолжение третьей. На этой прямой лежат точки и причем на стороне должна лежать точка на стороне – точка и на продолжении – точка

Затем записываем равенство так, как будто «обходим» весь треугольник от точки к точкам и и затем возвращаемся в точку Но по дороге нам встречаются точки и – их тоже включаем в формулу.

В некоторых задачах полезна обратная теорема Менелая.

Теорема (Менелая, обратная). Пусть дан треугольник Предположим, что точка лежит на стороне точка лежит на стороне а точка лежит на продолжении стороны причём про эти точки известно, что

Тогда эти точки лежат на одной прямой.

Как правило, не так-то просто бывает доказать, что три точки лежат на одной прямой. Обычно мы используем для доказательства такого факта косвенные методы. Например, если для точек и выполняется равенство: – то это означает, что точка лежит на отрезке Или, если нам удается доказать, что угол – развернутый, это и будет означать, что точки и лежат на одной прямой. Обратная теорема Менелая дает еще один способ доказательства того, что три точки – в данном случае и – лежат на одной прямой.

Теорема Чевы

Пусть точки и лежат соответственно на сторонах и треугольника причем отрезки и пересекаются в одной точке. В этом случае выполняется равенство:

Обратная теорема Чевы:

Теорема (Чевы, обратная). Пусть точки лежат соответственно на сторонах и треугольника причём

Тогда отрезки и пересекаются в одной точке.

Как применяются теоремы Менелая и Чевы?

Вот задача Профильного ЕГЭ по математике 2020 года (№16), Санкт-Петербургский вариант.

На сторонах и треугольника отмечены точки и соответственно, причём Отрезки и пересекаются в точке

а) Докажите, что — параллелограмм.
б) Найдите если отрезки и перпендикулярны,

Докажем пункт (а) с помощью теоремы Менелая:

Это значит, что по двум углам и то есть

Прямая пересекает две его стороны и продолжение третьей стороны

По теореме Менелая,

по углу и двум сторонам, отсюда

— параллелограмм по определению.

Мы доказали то, что требовалось в пункте (а).
Но что делать, если теоремы Менелая и Чевы вы не проходили в школе? Ничего страшного, докажем без теорем Менелая и Чевы. Их легко заменят подобные треугольники.

Докажем, что — параллелограмм.

Тогда по углу и двум пропорциональным сторонам,

Это значит, что по углу и двум сторонам и

Получим, что в четырёхугольнике :

Как видим, эти решения примерно одного уровня сложности.
А вот в пункте (б) нет необходимости применять теоремы Чевы и Менелая. Он легко решается с помощью обычной школьной геометрии.

Поскольку получим, что — прямоугольный.

Мы доказали в пункте (а), что — трапеция, причём

Тогда — параллелограмм (по признаку паралелограмма)

по теореме Пифагора из

Найдём из по теореме косинусов.

Вот еще одна задача, которую можно решить как с помощью теоремы Чевы, так и без нее.

На сторонах прямоугольного треугольника с прямым углом построены во внешнюю сторону квадраты и Докажите, что:

а) прямые и отсекают от катетов треугольника равные отрезки
б) прямые и высота треугольника проведённая из вершины пересекаются в одной точке.

Пункт (а) доказывается легко.

Решим пункт (б) с помощью теоремы Чевы:

Запишем, чему равны длины отрезков Для длин и воспользуемся тем, что в прямоугольном треугольнике каждый катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.

Проверим выполнение равенства

Равенство выполняется.
Согласно теореме Чевы, это значит, что и пересекаются в одной точке.
А вот как решается эта задача без теоремы Чевы, с помощью векторов:

Математик Менелай Александрийский жил в I веке до нашей эры (Древний Рим).
Математик и инженер Джованни Чева – XVII век, Италия.

Как видим, теоремы Менелая и Чевы оказываются полезны в некоторых задачах. Очень хорошо, если вы знаете эти теоремы. Однако если они для вас непривычны, можно применить простой школьный прием – пары подобных треугольников.

Это полезно

В нашей статье вы найдете всю необходимую теорию для решения задания №9 ЕГЭ по теме «Графики функций». Это задание появилось в 2022 году в вариантах ЕГЭ Профильного уровня.

Источник

Высшая математика. Шпаргалка

Настоящее издание поможет систематизировать полученные ранее знания, а также подготовиться к экзамену или зачету и успешно их сдать.

Оглавление

Приведённый ознакомительный фрагмент книги Высшая математика. Шпаргалка предоставлен нашим книжным партнёром — компанией ЛитРес.

2. Условие нахождения трех точек на одной прямой. Уравнение прямой. Взаимное расположение точек и прямой. Пучок прямых. Расстояние от точки до прямой

3. Пусть имеются точка М (х₁, у₁) и некоторая прямая L, представленная уравнением у = ах + с. Уравнение прямой, проходящей параллельно данной прямой L через данную точку М:

Если прямая L задана уравнением Ах + Ву + С = 0, то параллельная ей прямая, проходящая через точку М, описывается уравнением А(х — х₁) + В(у — у₁) = 0.

Уравнение прямой, проходящей перпендикулярно данной прямой L через данную точку М:

Если прямая L задана уравнением Ах + Ву + С = 0, то параллельная ей прямая, проходящая через точку М(х₁, у₁), описывается уравнением А (у — у₁) — В(х — х₁) = 0.

4. Пусть даны две точки А₁ (х₁, у₁), А₂ (х₂, у₂) и прямая, заданная уравнением Ах + Ву + С = 0. Взаимное расположение точек относительно этой прямой:

1) точки А₁, А₂ лежат по одну сторону от данной прямой, если выражения (Ах₁ + Ву₁ + С) и (Ах₂ + Ву₂ + С) имеют одинаковые знаки;

3) одна или обе точки А₁, А₂ лежат на данной прямой, если одно или оба выражения соответственно (Ах₁ + + Ву₁ + С) и (Ах₂ + Ву₂ + С) принимают нулевое значение.

5. Центральный пучок — это множество прямых, проходящих через одну точку М (х₁, у₁), называемую центром пучка. Каждая из прямых пучка описывается уравнением пучка у — у₁ = к (х — х₁) (параметр пучка к для каждой прямой свой).

Все прямые пучка можно представить уравнением: l(y — y₁) = m(x — x₁), где l, m — не равные одновременно нулю произвольные числа.

6. Пусть даны точка М (х₁, у₁) и прямая, заданная уравнением Ах + Ву + С = 0. Расстояние d от этой точки М до прямой:

Источник

Точка и прямая в начертательной геометрии с примерами

Содержание:

Для полного выявления наружных и внутренних форм деталей и их соединений вводят три и более плоскости проекций.

Введем в систему плоскостей

Чертеж точки

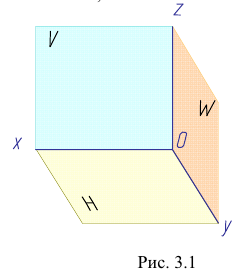
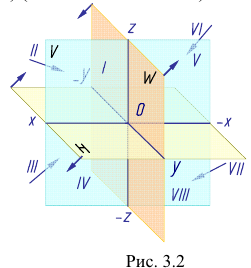
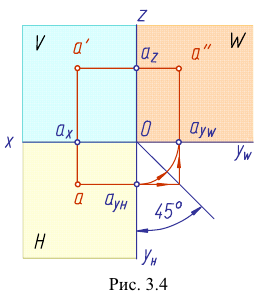
Данное наглядное изображение тонки в системе плоскостей Н, V и W (рис. 3.3) неудобно для черчения из-за сложности. Преобразуем его так, чтобы горизонтальная и профильная плоскости проекций совпали с фронтальной плоскостью проекций, образуя одну плоскость чертежа (рис. 3.4).

Это преобразование осуществляют путем поворота вокруг оси х плоскости Н на угол 90° вниз и плоскости W на угол 90° вправо вокруг оси z. В результате указанного совмещения плоскостей получаем чертеж, называемый эпюр Монжа (от франц, — чертеж, проект).

На эпюре мы не можем показать пространственную картину рас­положения плоскостей проекций и точки. Но эпюр обеспечивает точность изображений при значительной простоте построений.

Таким образом, на комплексном чертеже трех ортогональных проекций точки

Положение точки в пространстве задается при помощи трех се координат (абсциссы ординаты и аппликаты то есть трех чисел, вы­ражающих расстояние от этой точки до координатных плоскостей проекций. Запись координат точки производят в такой форме: А (х, у, z). Положение точки на плоскости определяют две координаты: а(х,у); a'(x,z); a»(y,z).

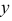
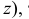
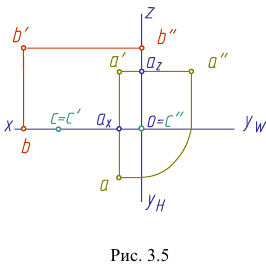
По отношению к плоскостям проекций точка может занимать как общее (точка А), так и частные (точки В и С) положения (рис. 3.5). Если точка лежит в плоскости проекций, то две ее проекции лежат на осях проекций (точка В). У такой точки одна ее координата равна нулю. Если точка принадлежит одновременно двум плоскостям проекций (точка С), то она ле­жит на оси проекций. Две ее проекции совпадают, а третья совпадает с точкой О — началом координат. В атом случае две ее координаты равны нулю. Если точка принадлежит трем плоскостям проекций, то она расположена в начале координат.

Взаимное положение двух точек. Условия видимости на чер­теже

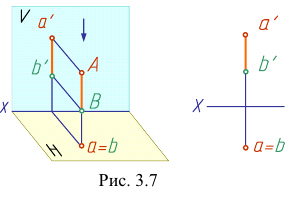
Ясно, что если две точки лежат на одной проецирующей прямой, то одна из них закрывает другую. Как определить, какая из них будет видимая и какая невидимая?

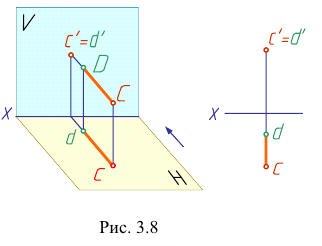
Из двух горизонтально- конкурирующих точек на горизонтальной плоскости видима та, которая расположена в пространстве выше. Анализируя положение фронтальных проекций точек (рис. 3.7), определяем, что точка А имеет большую координату z, чем точка В.

Из двух фронтально- конкурирующих точек на фронтальной плоскости проекций будет видима та, которая расположена ближе к наблюдателю, стоящему лицом к фронтальной плоскости проекций (рис. 3.8).

Из двух профильно-конкурирующих точек на профильной плоскости проекций бу­дет видима та точка, которая расположена левее.

Итак, если на чертеже одноименные проекции точек не совпадают или совпадает только одна пара проекций, то такие точки в пространстве не совпадают, а удалены друг от друга на определенное расстояние (рис. 3.7, 3.8).

Чертёж отрезка прямой. Прямые частного положения

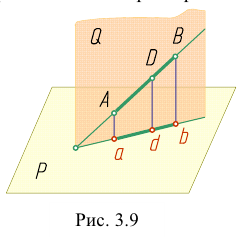
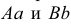
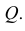
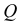
Наглядное изображение отрезка АВ прямой и его ортогональное проецирование на плоскость Р показано на рис. 3.9. Рассмотрим ортогональное проецирование отрезка АВ с учетом свойств параллельного проецирования. Проецирующие прямые образуют проецирующую плоскость Линия пере­сечения плоскостей и Р проходит через проекции а и b точек А и В на плоскости ­ проекций Р. Эта линия и является единственной проекцией прямой АВ на плоскости проекций Р.

Относительно плоскостей проекции прямая может занимать различные положения:

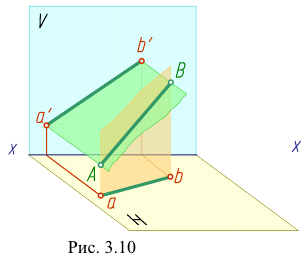
Прямую, не параллельную ни одной из плоскостей проекций, называют прямой общего положения (рис. 3.9 — 3.11).

Прямую, параллельную одной из плоскостей проекций или двум плоскостям проекций (то есть перпендикулярную третьей), называют прямой частного положения.

Различают три вида таких прямых.

Прямая АВ параллельна плоскости Н

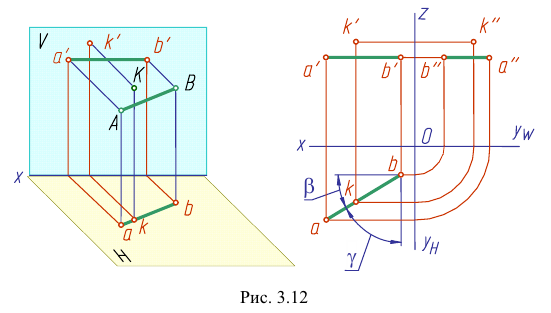
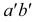
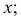
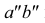
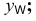
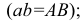
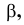
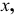
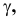
Такую прямую называют «горизонтальной прямой» (рис. 3.12). Фронтальная проекция прямой параллельна оси профильная проекция параллельна оси длина горизонтальной проекции отрезка равна длине самого отрезка угол образованный горизонтальной проекцией и осью проекции равен углу наклона прямой к фронтальной плоскости проекций; угол образованный горизонтальной проекцией и осью проекции равен углу наклона прямой к профильной плоскости проекций:

Прямая CD параллельна плоскости V

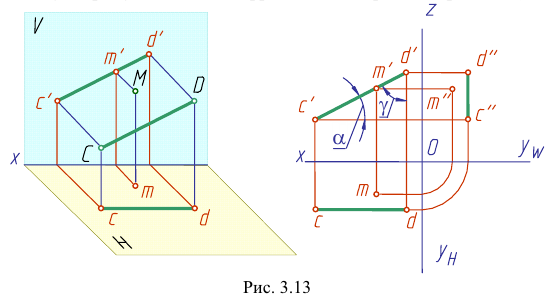
Такую прямую называют «фронтальной прямой» (рис. 3.13).

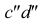
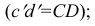
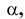
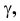
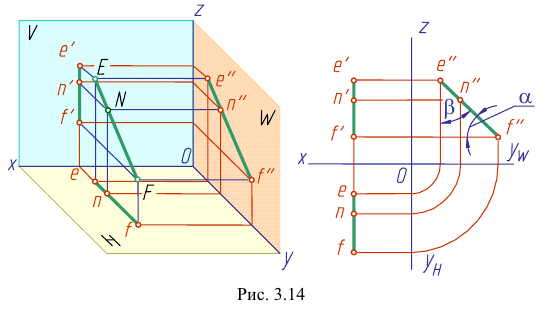
Горизонтальная проекция прямой cd параллельна оси х; профиль­ная проекция параллельна оси z; длина фронтальной проекции отрезка равна длине самого отрезка угол образованный фронтальной проекцией и осью проекций х, равен углу наклона прямой к горизонтальной плоскости проекций; угол образованный фронталь­ной проекцией и осью z, равен углу наклона прямой к профильной плоскости проекций:

Прямая EF параллельна плоскости IF

Такая прямая носит название «профильная прямая» (рис. 3.14).

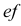
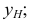
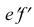
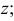
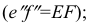
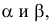
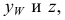
Горизонтальная проекция прямой параллельна оси фронтальная проекция параллельна оси длина профильной проекции отрезка равна длине самого отрезка углы образованные профильной проекцией с осями равны углам наклона прямой к горизонтальной и фронтальной плоскостям проекций соответственно:

Следовательно, каждая линия уровня проецируется в истинную величину на ту плоскость проекции, которой она параллельна. На ту­ же плоскость проекций проецируются без искажения и углы, которые эта прямая образует с остальными двумя плоскостями проекций.

На рис. 3.15 приведены чертежи прямых, перпендикулярных плоскостям проекций. Такие прямые называются проецирующими прямыми. Различают три вида таких прямых.

Прямая АВ перпендикулярна плоскости Н

Прямая CD перпендикулярна плоскости V

Прямая EF перпендикулярна плоскости W

Из чертежа видно, что проецирующая прямая является вместе с тем и прямой двойного уровня, так как она параллельна одновременно двум другим плоскостям проекций

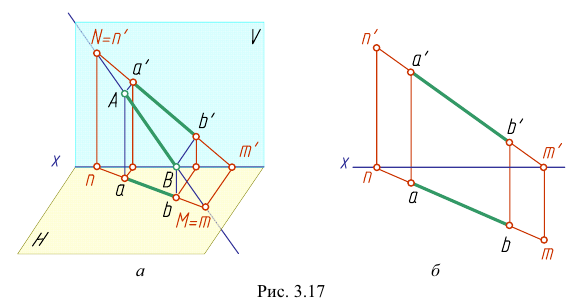
Взаимное положение точки и прямой

Точка и прямая в пространстве могут быть различно расположены относительно друг друга и плоскости проекций.

Если точка в пространстве принадлежит прямой, то ее проекции принадлежат соответствующим проекциям этой прямой.

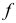
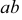
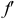
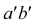
Рассмотрим еще раз это положение на плоскостном чертеже (рис. 3.16). Точка F принадлежит прямой АВ, так как горизонтальная проекция точки принадлежит горизонтальной проекции прямой, а фронтальная проекция точки принадлежит фронтальной проекции пря­мой:

Точка С лежит над прямой АВ, точка D лежит под прямой АВ. точка Е лежит за прямой АВ.

Следы прямой

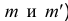
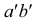
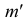
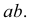
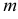
Чтобы построить на плоскостном чертеже горизонтальный след прямой (точки , надо продолжить фронтальную проекцию прямой до пересечения с осью х (точка ). Затем через нес провести перпендикуляр к оси х до пересечения с продолжением горизонтальной проекции Точка — горизонтальная проекция горизонтального следа.

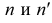
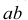
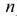
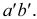
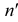
Для построения проекций фронтального следа (точек ) необ­ходимо продолжить горизонтальную проекцию прямой до пересечения с осью х (точка ). Затем через нес провести перпендикуляр к оси х до пересечения с продолжением фронтальной проекции Точка — фронтальная проекция фронтального следа. Построение проекций следов прямой показано на рис. 3.17, б.

Прямая может пересекать и профильную плоскость проекций, то есть иметь профильный след. Этот след на профильной плоскости проекций совпадает со своей проекцией. Фронтальная и горизонтальная проекции его лежат соответственно на осях

Взаимное положение двух прямых

Прямые в пространстве могут занимать различные взаимные поло­жения:

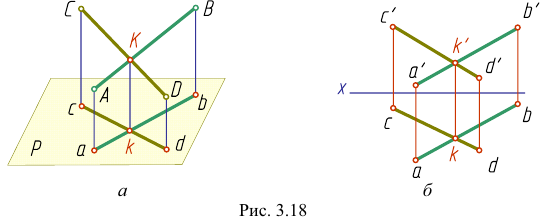
Пересекающиеся прямые

Если прямые пересекаются, то их одноименные проекции пересекаются между собой и точки пересечения проекций лежат на одной линии связи.

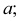
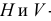
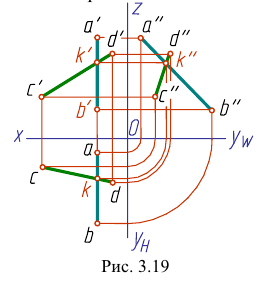
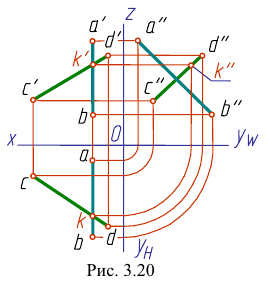
Наглядное изображение двух прямых АВ и CD, пересекающихся в точке К, приведено на рис. 3.18, их чертеж в системе плоскостей -на рис. 3.18, б.

Если одна из прямых профильная, то чтобы ответить на вопрос, пересекаются ли прямые, следует построить их профильные проекции.

На рис. 3.19 все проекции точки 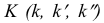одновременно принадлежат проекциям прямой АВ и прямой CD. Это значит, что прямые АВ и CD пересекаются.

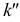
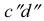
На рис. 3.20 профильная проекция точки К принадлежит профильной проекции и не принадлежит профильной проекции

Это значит, что прямые АВ и CD не пересекаются, они скрещиваются.

Параллельные прямые

О параллельности прямых в пространстве можно судить по параллельности их одноименных проекций на двух плоскостях проекций.

При этом нужно учитывать некоторые условия.

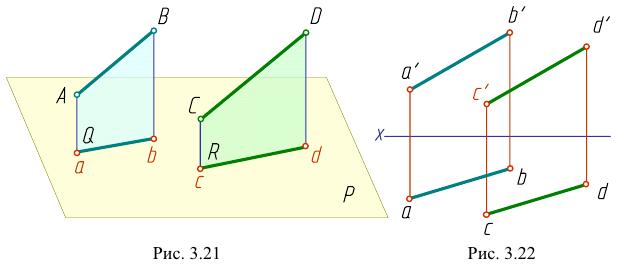
Для прямых общего положения:

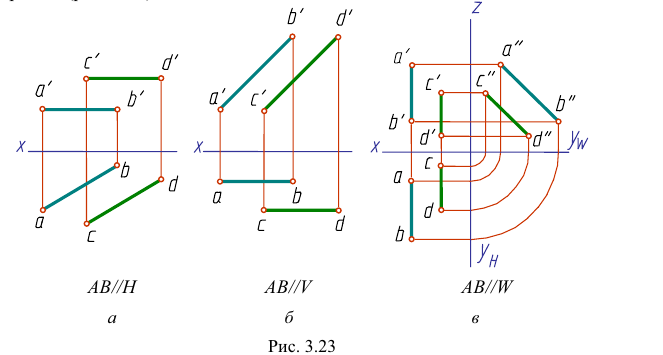
Если одноименные проекции прямых общего положения парал­лельны в системе двух любых плоскостей проекций, то прямые парал­ лельны (рис. 3.22).

Для прямых частного положения:

Если одноименные проекции прямых параллельны одной из осей проекций, то прямые параллельны при условии параллельности одноименных проекций на той плоскости проекций, которой параллельны прямые (рис. 3.23).

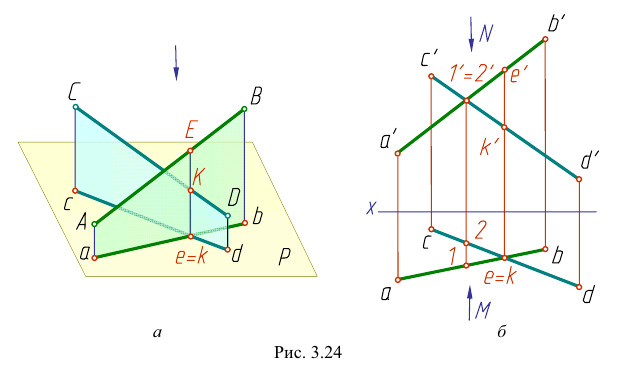
Скрещивающиеся прямые

Если прямые в пространстве нс пересекаются, а скрещиваются (рис. 3.24), то хотя на чертеже их одноименные проекции и пересекаются, но точки пересечения проекций не лежат на одной линии связи. Эти точки не являются общими для прямых.

Сравнивая положение таких точек, определяют, какая из изображенных на чертеже прямых выше другой или ближе другой к наблюдателю. На рис. 3.24, а видно, что точка Е (принадлежащая прямой АВ) расположена выше точки К (принадлежащей прямой CD). При взгляде сверху по указанной стрелке точка Е закрывает точку К. Соответственно и на чертеже (рис. 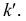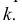3.24, б) фронтальная проекция е’ расположена выше фронтальной проекции При взгляде сверху по стрелке N при проецировании на плоскость Н точка е закрывает точку Прямая АВ проходит над прямой CD.

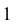
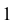
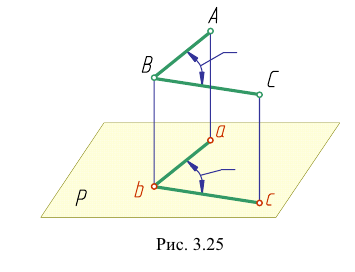
На плоскости V совпадают фронтальные проекции 1′ и 2′ точек прямых АВ и CD. При взгляде спереди по стрелке М видно, что точка прямой АВ находится ближе к наблюдателю, и при проецировании на плоскость V точка прямой АВ закрывает точку 2 прямой CD. Прямая АВ расположена ближе к наблюдателю. Рассмотренные точки являются конкурирующими, так как они лежат на одной линии связи, но на разных прямых.

Проецирование плоских углов

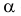
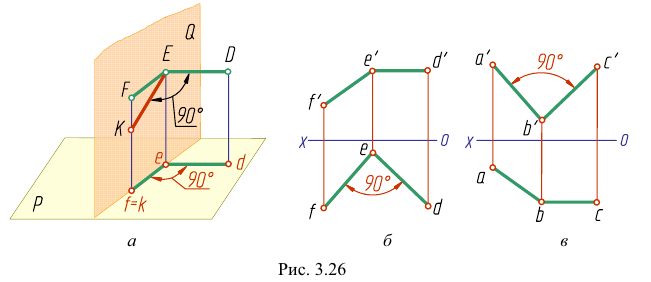
Любой линейный угол образуется двумя пересекающимися пря­мыми. На плоскости проекций он проецируется в общем случае с искажением. Однако, если обе стороны угла параллельны какой-либо плоскости проекций, то на эту плоскость угол проецируется без искажения. Например, стороны угла АВС (рис. 3.25) параллельны горизонтальной плоскости Р. поэтому угол спроецировался на нее без изменений.

Исключение составляет прямой угол. Он проецируется в истинную величину даже тогда, когда лишь одна из его сторон параллельна плоскости проекций. Рассмотрим теорему о проецировании прямого уг­ла.

Доказательство. Пусть угол 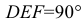и расположен так, что обе его стороны параллельны плоскости Р(рис. 3.26, а). Тогда, как и всякая фигура, лежащая в плоскости, параллельной Р, данный угол спроецируется на Р без искажения, то есть его проекция

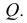
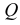
Через прямые EF и Ее проведем дополнительную плоскость Плоскость перпендикулярна плоскости Р.

Но, как видно непосредственно из чертежа, только одна сторона DE угла DEK параллельна плоскости Р.

Вторая сторона его ЕК наклонна к плоскости Р.

Итак, для того чтобы прямой угол проецировался в натуральную величину, достаточно, чтобы одна его сторона была параллельна плоскости проекций (рис. 3.26, б, в).

Определение истинной величины отрезка прямой

Отрезки прямых общего положения не проецируются в истинную величину ни на одну из плоскостей проекций. Однако в ряде задач необходимо определить по чертежу длину отрезка прямой общего положения и углы наклона прямой к плоскостям проекций.

В этом случае используют способ построения прямоугольного треугольника.

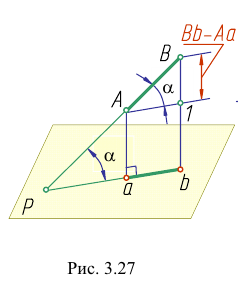
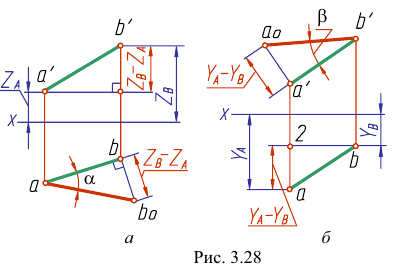
Определим истинную величину отрезка АВ и угол наклона его к плоскости Н (угол 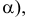если известны две проекции отрезка (рис. 3.28, а).

На рис. 3.28, 6 показано определение истинной величины отрезка АВ и угла наклона его к плоскости V- угла

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник