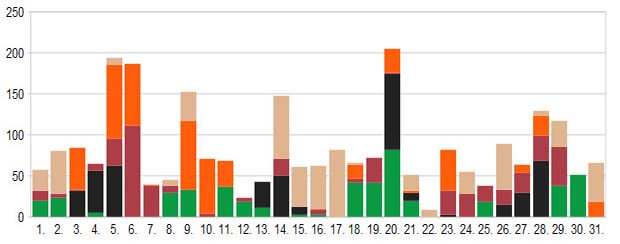
Средневзвешенное число обыкновенных акций
МСФО, Дипифр
Показатель EPS — формула расчета. Базовая прибыль на акцию
Формула расчета базовой прибыли на акцию
Базовая EPS показывает, какая величина чистой прибыли за период приходится на одну обыкновенную акцию в обращении. Это относительный показатель прибыльности, который в отличие от абсолютной величины чистой прибыли считается более надёжным индикатором успешности компании. Стандарт МСФО IAS 33 «Прибыль на акцию» был введен в действие с целью унифицировать практику расчета показателя EPS.
В самом простом случае формула EPS выглядит так:
EPS = Чистая прибыль за период/Количество обыкновенных акций, где
Для России, где структура капитала большинства компаний является довольно простой и состоит только из обыкновенных акций, расчет прибыли на акцию не вызывает больших сложностей. Однако, в западной практике, где существуют разные типы привилегированных акций и где обычной практикой являются выпуск на рынок и выкуп с рынка обыкновенных акций, расчет базовой EPS является более сложным упражнением.
Какую прибыль надо брать для расчета базовой EPS? Числитель формулы.
Во-первых, это чистая (=посленалоговая) прибыль, во-вторых, это прибыль, приходящаяся на долю держателей обыкновенных акций.
Чтобы найти величину прибыли для расчета базовой EPS, из величины чистой прибыли необходимо исключить дивиденды по привилегированным акциям. В общем случае, привилегированные акции — это финансовые инструменты, не обладающие правом голоса, но обладающие определёнными привилегиями: а) дивиденды по ним являются фиксированной суммой, а не долей в прибыли как у обыкновенных акционеров; б) в случае банкротства владельцы таких акций имеют преимущество над обыкновенными акционерами при возмещении убытков. По сути привилегированная акция это нечто среднее между обыкновенной акцией и облигацией.
Не знаю, будет ли такое на экзамене, но в западной практике различают два типа привилегированных акций:
В первом случае дивиденды должны быть выплачены в любом случае, поэтому они вычитаются из величины прибыли для расчета EPS вне зависимости от того, объявлены они или нет. По некумулятивным привилегированным акциям дивиденды уменьшают величину прибыли в числителе формулы EPS только в том случае, если они были объявлены.
Расчет средневзвешенного количества акций — коэффициент эмиссии. Знаменатель формулы.
Самое сложное в задачах на расчет прибыли на акцию – это определение знаменателя в формуле EPS. Средневзвешенное количество акций за период может увеличиться в течение периода в результате эмиссии (выпуска) новых обыкновенных акций. Выкуп акций с рынка наоборот приводит к уменьшению этой величины.
Рассмотрим следующие варианты эмиссии акций:
В всех трех случаях на момент эмиссии произойдет падение прибыли на акцию, потому что знаменатель формулы увеличится.
В данной статье я использую метод расчета средневзвешенного количества акций через коэффициенты эмиссии для всех трех вариантов. Внешне этот метод кажется непохожим на тот, который прописан в стандарте и есть в учебниках. Однако, математически это абсолютно тот же метод расчета, который даёт правильный результат.
1. Простая эмиссия акций по рыночной стоимости
При данной эмиссии в обращении становится больше акций за рыночную цену. Приведу пример из стандарта МСФО 33, который повторяется во всех учебниках:
Как рассчитать средневзвешенное количество обыкновенных акций в обращении за год?
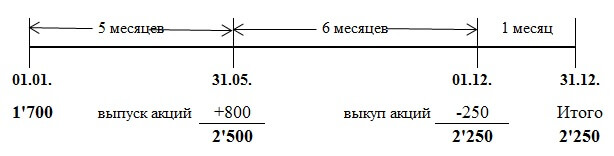
Поможет графическое представление условия примера:
В стандарте МСФО 33 приведены два способа расчета, но я предлагаю использовать один, на мой взгляд, более простой:
1,700 х 5/12 + 2,500 х 6/12 + 2,250 х 1/12 = 2, 146 штук.
Как видно из формулы, количество акций нужно умножить на количество месяцев до следующего события (выпуска или выкупа), делённые на 12. То есть, количество акций взвешивается пропорционально периоду, в течение которого оно не менялось.
2. Выпуск прав (rights issue)
Эта эмиссия дает право акционерам приобрести новые акции по цене ниже рыночной — нечто среднее между льготной (бесплатной) эмиссией и эмиссией по рыночной цене. Потому что компания хотя и получает возмещение за выпущенные акции, но это возмещение будет меньше, чем если бы выпуск акций проходил на рыночных условиях.
Пример 4 из стандарта МСФО 33.
На 1 января в обращении было 500 обыкновенных акций. 1 января компания объявила льготную эмиссию 1 к 5 по цене 5 долларов за новую акцию. 1 марта — последний день для выкупа прав по предложенной цене. Рыночная цена одной обыкновенной акции перед 1 марта (закрытием периода выкупа прав) была равна 11 долларам. Как рассчитать средневзвешенное количество акций за год?
Во-первых, 1 марта добавятся 100 (500/5) новых обыкновенных акций, таким образом, 500 акций будем умножать на 2/12, а 600 акций на 10/12.
Во-вторых, поскольку это выпуск прав и цена размещения ниже рыночной, то стандарт предписывает использовать коэффициент эмиссии (KЭ). И формула для расчета средневзвешенного количества акций будет такой:
500 х 2/12 х KЭ + 600 х 10/12 = Х
*КЭ — не является общепринятым сокращением
Коэффициент эмиссии считается как отношение рыночной цены акции к теоретической цене после выпуска прав. В данном примере рыночная цена равна 11 долларам, а цена после выпуска прав (красное) рассчитывается следующим образом:
Алгоритм расчета такой:
Теоретическая цена после выпуска прав: 6,000/600 = 10 долларов.
Коэффициент данной эмиссии (КЭ): 11/10
Средневзвешенное количество акций за год будет равно: 500 х 2/12 х 11/10 + 600 х 10/12 = 591,67 штук.
а) 5 х 11 = 55, б) 1 х 5 = 5, в) 55+5 = 60, г) 60/6 = 10
3. Бесплатная эмиссия акций (bonus issue)
О терминологии. Я хотела назвать этот вид эмиссии льготным, однако в стандарте льготной эмиссией называется любая эмиссия, если выпуск акций происходит меньше рыночной цены (т.е. выпуск прав тоже льготная эмиссия). Поэтому решила использовать слова «бонусная» или «бесплатная» эмиссия. Но хочу предупредить, что это не общепринятые термины, я использую эти слова только для простоты объяснения.
Иногда компании размещают обыкновенные акции среди существующих акционеров без возмещения их стоимости. Как говорилось в одном нашем известном советском мультфильме: «безвозмездно, то есть даром». Как такая эмиссия повлияет на расчет средневзвешенного количества акций для EPS?
Снова изменим предыдущий пример 4.
На 1 января в обращении было 500 обыкновенных акций. А 1 марта компания провела льготную эмиссию в соотношении 1 новая акция на каждые 5 обыкновенных акций в обращении. Рыночная цена одной обыкновенной акции перед 1 марта была равна 11 долларам.
Шкала времени не изменится, а вот таблица будет немного другой:
Теоретическая цена после льготной эмиссии: 5,500/600 = 9,1666 долларов.
Коэффициент данной эмиссии (КЭ): 11/9,1666 = 1,2
Средневзвешенное количество акций за год: 500 х 1,2 х 2/12 + 600 х 10/12 = 600 штук.
Если умножить 500 на коэффициент 1,2, то получится 600. И формулу выше можно переписать по-другому: 600 х 2/12 + 600 х 10/12 = 600 штук.
То есть при бесплатном выпуске акций получается, что новое количество акций (в данном случае 600 штук) было всегда. Математически это так.
Две эмиссии акций в одном примере — как найти средневзвешенное количество за год?
Как показано выше, все три типа эмиссии акций можно учесть с использованием коэффициента эмиссии (КЭ):
Что будет, если в течение года эмиссия акций будет не одна?
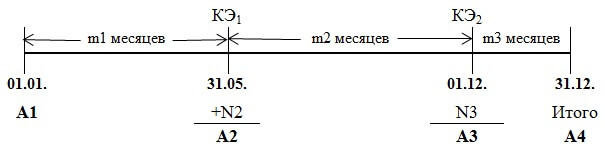
Графически задачу с несколькими эмиссиями можно представить в виде шкалы времени так:
Для любителей длинных формул: если в течение года произошло несколько эмиссий обыкновенных акций, то в общем виде формулу для расчета средневзвешенного количества акций можно записать так (не является общепринятой!):
А1 х КЭ1 х КЭ2 х m1/12 + A2 х КЭ2 х m2/12 + A3 х m3/12, где
КЭ — коэффициент эмиссии, А — количество акций в тот или иной период времени, m — количество месяцев между эмиссиями, N — количество новых акций, то есть, А1+N2 = A2, A2+N3 = A3, А3 = А4. Все обозначения не являются общепринятыми и придуманы мной за неимением других.
Пример расчета базовой EPS с простой и льготной эмиссиями в течение года
Чтобы было понятнее, рассмотрим пример из задачи экзамена ACCA F7 в июне 2006 года.
Задание. Рассчитать средневзвешенное количество акций в отчетном периоде и базовую прибыль на одну акцию.
В данном примере нужно учесть две эмиссии акций в течение года: через 3 месяца эмиссия по рыночной стоимости, ещё через 6 месяцев — «бесплатная» эмиссия. Всё становится понятнее, когда все цифры из условия задачи нанесены на шкалу времени:
Коэффициент первой эмиссии по рыночной стоимости равен 1 (всегда), коэффициент бесплатной эмиссии равен 60,000/48,000 = 1,25 (количество акций «после»/количество акций «до»)
Средневзвешенное количество акций за год будет равно:
40,000 х КЭ1 х КЭ2 х 3/12 + 48,000 х КЭ2 х 6/12 + 60,000 х 3/12 = 57,500
40,000 х 1 х 1,25 х 3/12 + 48,000 х 1,25 х 6/12 + 60,000 х 3/12 = 57,500
Прибыль на акцию: 13,800/57,500 = 0,24 доллара или 24 цента.
При решении данной задачи я использовала формулу с коэффициентами, а в официальном ответе приведен немного другой способ расчета. Но ответ получается одинаковым, потому что оба способа являются правильными.
ВНИМАНИЕ: Поскольку данный сайт не является официальным учебным пособием, я могу использовать любые приёмы, какие считаю нужными, для объяснения материала. Полезно бывает, взглянуть на расчёты под другим углом зрения. Но я не уверена, что представленный здесь метод расчета средневзвешенного количества акций на экзамене будет оценен правильно. Всё-таки проверяющие экзамен маркеры учились по учебникам, в которых метод получения ответа (при наличии бесплатной эмиссии) внешне несколько отличается. Просто имейте это в виду. Хотя правильный результат расчётов должен говорить сам за себя.
Выдержка из официального ответа
Выпуск на 1 июля 2003 года по полной рыночной стоимости должен быть взвешен: 40 млн х 3/12 + 48 млн х 9/12 = 46 млн. Без учета бонусного выпуска прибыль на акцию составит 30 центов ($13,8 млн/46 млн.).
Бонусный выпуск 1 к 4 приведет к появлению 12 млн новых акций, следовательно, общее число обыкновенных акций составит 60 млн. Разводняющий эффект бонусного выпуска снизит прибыль на акцию до 24 центов (30 центов х 48 млн/60 млн).
Прямые и обратные коэффициенты эмиссии
Все коэффициенты эмиссии, которые рассматривались выше, называются прямыми и используются для расчета средневзвешенного количества акций за период. Величина 1/КЭ представляет собой обратный коэффициент эмиссии, который нужен для получения сравнительных данных. Если в отчётном периоде произошел выпуск прав, то это повлияет как на величину EPS в текущей отчетности МСФО, так и на величину EPS в предыдущей отчетности. Чтобы получить сравнительные данные по EPS за предыдущий год, надо пересчитать EPS прошлого года, умножив её на обратный коэффициент эмиссии отчетного года. Если было две эмиссии и два коэффициента, то для пересчёта нужно использовать оба обратных коэффициента.
Базовая прибыль на акцию — ещё один пример расчета
Попробуем решить еще одну задачу, на этот раз из экзамена Дипифр, март 2009 года, вопрос 4, 6 баллов.
(b) Компания «Ипсилон» ежегодно готовит финансовую отчетность за год, заканчивающийся 31 декабря. Чистая прибыль компании за год, закончившийся 31 декабря 2008 года, составила 12 млн. долларов. Этот показатель был сформирован после вычета финансовых расходов, относящихся к привилегированным акциям, в размере 600,000 долларов. По состоянию на 1 января 2008 года «Ипсилон» имела в обращении 30 млн. обыкновенных акций. 1 апреля 2008 года «Ипсилон» выпустила 20 млн. обыкновенных акций по полной рыночной стоимости. 1 октября 2008 года «Ипсилон» выпустила права на приобретение акций, предложив имеющимся акционерам компании (включая держателей акций, выпущенных 1 апреля 2008 года) приобрести 1 акцию за каждые 5, находящиеся в их собственности, по цене 2 доллара за акцию.
Этот выпуск был полностью выкуплен акционерами. Рыночная стоимость одной обыкновенной акции «Ипсилон» на 1 октября 2008 года непосредственно перед выпуском прав на приобретение акций была равна 2 долларам 30 центам. Прибыль на акцию, отраженная в финансовой отчетности за год, закончившийся 31 декабря 2007 года, составляла 22 цента.
Задание: Рассчитайте прибыль на акцию (включая сравнительные данные), которая должна быть отражена в финансовой отчетности «Ипсилон» за год, закончившийся 31 декабря 2008 года.
Решение задачи
Числитель формулы для расчета прибыли на акцию — 12,000,000 долларов. В условии сказано, что эта цифра чистой прибыли уже скорректирована на дивиденды привилегированным акционерам, значит, дальнейших корректировок не требуется.
В течение года было две эмиссии акций: через 3 месяца от начала года простая эмиссия по рыночной стоимости, ещё через полгода — выпуск прав.
Коэффициент эмиссии по рыночной цене равен 1 (единице).
Коэффициент эмиссии для выпуска прав будет равен 2,30/2,25:
Расчёт средневзвешенного количества акций будет таким:
30,000 х 1 х 2,30/2,25 х 3/12 + 50,000 х 2,30/2,25 х 6/12 + 60,000 х 3/12 = 48,222 штук.
Базовая прибыль на акцию: 12,000,000/48,222 = 0,249 или 24,9 цента
Сравнительные данные за прошлый год нужно умножить на обратные коэффициенты эмиссии:
22 х 1 х 2,25/2,3 = 21,5 (для единицы обратный коэффициент тоже равен 1)
МСФО 33 «Прибыль на акцию» на экзаменах Дипифр и ACCA
На экзамене Дипифр данная тема появлялась всего два раза — в марте 2009 года на 25 баллов (русскоязычный экзамен) и в декабре 2010 года на 15 баллов (глобально). В обоих случаях это было задание, включающее в себя как теоретические вопросы, так и расчет обоих показателей EPS — базовой и разводненной прибыли на акцию. В новом формате экзамена Дипифр, введенном в действие с июня 2011 года, данный стандарт не появился ни разу. Возможно поэтому многие преподаватели и слушатели курсов Дипифр ожидают задачи на расчет прибыли на акцию в ближайшее время.
В народном прогнозе на декабрьскую сессию Дипифр 2016 года на данный момент МСФО 33 занимает второе место с показателем 23%. Такой же прогноз к июню 2016 года МСФО 33 занял первое место в рейтинге ожиданий с 35% голосов.
Честно говоря, я скептически отношусь к тому, что прибыль на акцию появится на экзамене Дипифр в ближайшее время. По большому счету расчет прибыли на акцию не имеет отношения к бухгалтерскому учету. МСФО 33 описывает алгоритм расчета числового показателя, не более того. Наш же экзаменатор стремится включать в экзамен задачи, требующие умения рассуждать и объяснять основные принципы бухгалтерского учета, заложенные в международные стандарты.
Хотя, возможно, я ошибаюсь, и Пол Робинс просто ждёт удобного момента, чтобы включить такую задачу в экзамен. Если расчет прибыли на акцию появится на экзамене Дипифр, я думаю, это будет упрощение экзамена с точки зрения нашего экзаменатора, поскольку рассчитать несколько цифр гораздо проще, чем написать объяснения по теоретическому вопросу.
Что касается основной программы ACCA, то расчет показателя EPS несколько раз появлялся в заданиях бумаги F7: июнь 2006, декабрь 2009, июнь 2011 годов, но расчетной задачи не было ни разу на экзамене более высокого уровня P2 (если я ничего не пропустила).
Математика — это гимнастика для ума
Надеюсь, что данная статья не получилась слишком нудной, хотя и не уверена в этом. Слишком много формул, слишком много расчетов. И всё-таки, думаю, что задачи на эту тему будут, скорее, подарком от экзаменатора, чем наоборот. Ведь для того, чтобы правильно рассчитать прибыль на акцию, надо всего лишь помнить алгоритм расчёта. А для того, чтобы написать ответ на теоретический вопрос, надо понять, что хочет увидеть в ответе Пол Робинс.
«Если математика не кажется людям простой, это лишь потому, что люди не понимают, насколько сложна жизнь». Джон фон Нейман, математик
Об уникальности публикаций
Все статьи на данном сайте написаны мной от начала и до конца. И тому есть подтверждение. Именно поэтому я, к сожалению, редко пишу новые статьи — это требует времени, которое в дефиците. Я встречала перепечатки материалов данного сайта на других интернет ресурсах. Некоторые копии имеют ссылку на оригинал на моём сайте. Но если на других сайтах в интернете не стоит ссылка на оригинальную публикацию здесь, то знайте, это ни что иное как плагиат. Тоже самое относится и к заимствованиям не в интернете. Но такова уж судьба у всех пишущих и публикующих что-либо в сети.
Другие статьи, которые могут быть интересны:
Термины МСФО: Средневзвешенное количество обыкновенных акций в обращении
Татьяна Мошкина,
консультант-преподаватель Академии бизнеса «Эрнст энд Янг»
Средневзвешенное количество обыкновенных акций в обращении (Weighted average number of ordinary shares outstanding)
Расчет средневзвешенного количества обыкновенных акций, находящихся в обращении в течение периода, осуществляется следующим образом:
При этом нужно иметь в виду, что акции могут выпускаться как по рыночной цене (за денежные средства, в обмен на пакет акций другой компании, в качестве погашения обязательств), так и без оплаты (в виде льготной эмиссии, выпуска прав (rights issue), дробления или консолидации акций).
Во втором случае выпуск акций не приводит к изменению активов компании, поэтому при расчетах учитывается, что новые акции были в обращении в течение всего отчетного периода.
Таким образом, средневзвешенное количество обыкновенных акций в обращении можно получить путем умножения количества акций в обращении до даты выпуска на удельную продолжительность периода, в течение которого это число акций находилось в обращении, и коэффициент льготной эмиссии. Он рассчитывается как отношение числа акций после эмиссии, деленное на количество акций до нее.
В случае выпуска прав компания дает акционеру возможность купить ее акции по цене ниже рыночной, а значит, эмиссия содержит как рыночный элемент, так и элемент без оплаты. В данном случае средневзвешенное количество обыкновенных акций в обращении является произведением числа акций в обращении до даты выпуска, удельной продолжительности периода, в течение которого они находились в обращании и коэффициента выпуска прав. Его находят с помощью деления стоимость акций до эмиссии на стоимость акций после нее.
Средневзвешенные акции и акции в обращении
Опубликовано 10.06.2021 · Обновлено 12.06.2021
Понимание разницы между средневзвешенными акциями и акциями в обращении жизненно важно для инвесторов, пытающихся создать портфель, который будет работать в соответствии с их ожиданиями. Эти два расчета предоставляют информацию о том, насколько хорошо компания работает с течением времени.
Акции в обращении
Акции, находящиеся в обращении, относятся к акциям, которые в настоящее время принадлежат инвесторам. Сюда также входят акции, принадлежащие широкой публике, и акции с ограниченным доступом, принадлежащие должностным лицам компании и инсайдерам. Количество находящихся в обращении акций изменяется, если компания выпускает новые акции, выкупает существующие акции или если опционы сотрудников конвертируются в акции.
Средневзвешенное количество акций
В средневзвешенные акций в обращении, или средневзвешенное акций в обращении, является расчет, который принимает во внимание любые изменения в количестве размещенных акций за определенный отчетный период. Инвесторы, вкладывая средства на длительный срок, часто формируют позицию в акции на несколько лет.
Цены на акции меняются ежедневно, поэтому желательно отслеживать стоимость акций, накопленных за многие годы. Если инвестор хочет рассчитать средневзвешенную цену, уплаченную за акции, он должен умножить количество акций, приобретенных по каждой цене, на эту цену, сложить эти значения, а затем разделить общую стоимость на общее количество акций.
В общем, средневзвешенное значение – это среднее значение, вычисленное путем усреднения каждой величины по назначенному весу для определения относительной важности каждой величины.
Средневзвешенное количество акций определяется путем умножения количества акций в обращении на процентную долю отчетного периода, для которого это количество применяется для каждого периода. Другими словами, в формуле берется количество акций, находящихся в обращении в течение каждого месяца, взвешенное по количеству месяцев, в течение которых эти акции находились в обращении.
Средневзвешенная цена на акцию
Инвесторы могут использовать средневзвешенные значения, если они сформировали позицию по определенной акции за период. Учитывая постоянно меняющиеся цены на акции, инвестор рассчитает средневзвешенную цену акций, уплаченных за акции.
Чтобы рассчитать средневзвешенную стоимость одной акции, инвестор может умножить количество акций, приобретенных по каждой цене, на эту цену, сложить эти значения, а затем разделить общую стоимость на общее количество акций.
Средневзвешенные значения также могут использоваться в других аспектах финансов, включая расчет доходности портфеля, учет запасов и оценку.
Средневзвешенное количество акций в обращении
Средневзвешенное количество акций в обращении используется для расчета ключевых финансовых показателей, таких как прибыль на акцию (EPS). Управленческие и финансовые аналитики уделяют особое внимание прибыли на акцию, поскольку она представляет собой прибыль, оставшуюся от операций, доступную акционерам. Например, базовая прибыль на акцию рассчитывается следующим образом:
Базовая прибыль на акцию = базовые средневзвешенные акции
С другой стороны, базовые средневзвешенные акции представляют собой вышеупомянутые средневзвешенные акции, находящиеся в обращении, за вычетом разводнения опционов на акции за определенный период. Для базовых средневзвешенных акций «базовые» по сути означает неразводняющие.
Разбавление происходит, когда компания выпускает дополнительные акции, которые уменьшают пропорциональную долю владения существующего инвестора в компании. Использование разводненных акций более информативно, чем использование базовых акций, потому что, если ценные бумаги конвертируются в обыкновенные акции, другими словами, происходит разводнение, доля инвестора в компании или их доля в общем круге акций сокращается.
Компаниям с простой структурой капитала необходимо сообщать только базовую прибыль на акцию. Те, у кого сложная структура (те, у которых есть потенциально разводняющие ценные бумаги), должны сообщать как базовую прибыль на акцию, так и разводненную прибыль на акцию.
Средневзвешенное число обыкновенных акций
II. Базовая прибыль (убыток) на акцию
3. Базовая прибыль (убыток) на акцию определяется как отношение базовой прибыли (убытка) отчетного периода к средневзвешенному количеству обыкновенных акций, находящихся в обращении в течение отчетного периода.
4. Базовая прибыль (убыток) отчетного периода определяется путем уменьшения (увеличения) прибыли (убытка) отчетного периода, остающейся в распоряжении организации после налогообложения и других обязательных платежей в бюджет и внебюджетные фонды, на сумму дивидендов по привилегированным акциям, начисленным их владельцам за отчетный период.
При исчислении базовой прибыли (убытка) отчетного периода не учитываются дивиденды по привилегированным акциям, в том числе по кумулятивным, за предыдущие отчетные периоды, которые были выплачены или объявлены в течение отчетного периода.
5. Средневзвешенное количество обыкновенных акций, находящихся в обращении в течение отчетного периода, определяется путем суммирования количества обыкновенных акций, находящихся в обращении на первое число каждого календарного месяца отчетного периода, и деления полученной суммы на число календарных месяцев в отчетном периоде.
Обыкновенные акции включаются в расчет их средневзвешенного количества с момента возникновения прав на обыкновенные акции у их первых владельцев, за исключением случаев, предусмотренных в пункте 7 настоящих Методических рекомендаций.
Для расчета средневзвешенного количества обыкновенных акций, находящихся в обращении, используются данные реестра акционеров общества на первое число каждого календарного месяца отчетного периода.
В 2000 г. в акционерном обществе «X» имело место следующее движение обыкновенных акций:
│ Дата │Размещение │Выкуп (приобретение) │Обыкновенные акции, │
│ │(количество │(кол-во выкупленных │находящиеся в обраще- │
│ │дополнитель-│(приобретенных) акций│нии (количество) │
│ │ных акций, │у акционеров) │ │
│31.12.│ 800 │ 400 │ 1400 │
Средневзвешенное количество обыкновенных акций, находящихся в обращении:
(1000 х 3 + 1800 х 6 + 1400 х 3) : 12 = 1500, или
6. Данные о средневзвешенном количестве обыкновенных акций, находящихся в обращении, корректируются в случаях:
а) размещения акционерным обществом обыкновенных акций без их оплаты, не влияющего на распределение прибыли между акционерами, в соответствии с пунктом 7 настоящих Методических рекомендаций;
б) размещения дополнительных обыкновенных акций по цене ниже рыночной стоимости в соответствии с пунктом 8 настоящих Методических рекомендаций.
В целях настоящих Методических рекомендаций рыночная стоимость ценных бумаг определяется в соответствии с Федеральным законом от 26 декабря 1995 г. N 208-ФЗ «Об акционерных обществах» (Собрание законодательства Российской Федерации, 1996, N 1, ст. 1).
Для целей обеспечения сравнимости средневзвешенного количества обыкновенных акций, находящихся в обращении на начало и конец отчетного периода, обыкновенные акции считаются размещенными на начало отчетного периода. При этом количество обыкновенных акций, находящихся в обращении до даты указанного размещения, при расчете их средневзвешенного количества увеличивается (уменьшается) в той же пропорции, в какой они были увеличены (уменьшены) в результате указанного размещения.
│ │ 1999 г.│ 2000 г. │ Обыкновенные акции, │
│ │ │ │находящиеся в обращении│
│01.06.2000 │ │ 1400 │ 2800 │
│обыкновенных акций в│ │ │ │
│Средневзвешенное │ 3000 │ 2800 │ │
│обыкновенных акций в│ │ │ │
│обращении с учетом│ │ │ │
В 2000 г. акционерное общество «X» проводит размещение дополнительных обыкновенных акций путем распределения их среди акционеров из расчета одна дополнительная акция на одну акцию в обращении.
8. При размещении обыкновенных акций по цене ниже их рыночной стоимости в случаях, предусмотренных Федеральным законом «Об акционерных обществах», для целей расчета базовой прибыли (убытка) на акцию все обыкновенные акции, находящиеся в обращении до указанного размещения, предполагаются оплаченными по цене ниже рыночной стоимости при соответствующем увеличении их количества.
Количество обыкновенных акций, находящихся в обращении до указанного размещения, корректируется в зависимости от соотношения рыночной стоимости на дату окончания указанного размещения и средней расчетной стоимости обыкновенных акций, находящихся в обращении.
Средняя расчетная стоимость обыкновенных акций, находящихся в обращении, определяется как частное от деления совокупной стоимости обыкновенных акций, находящихся в обращении на дату, следующую за датой окончания размещения, на их количество.
При этом совокупная стоимость обыкновенных акций складывается из:
рыночной стоимости обыкновенных акций, находящихся в обращении до размещения;
средств, полученных от размещения обыкновенных акций по цене ниже рыночной стоимости.