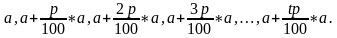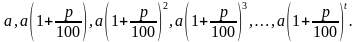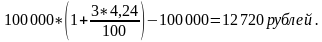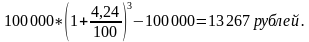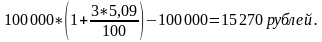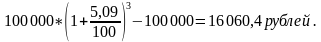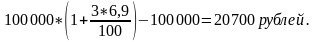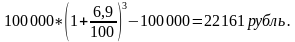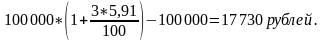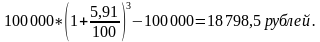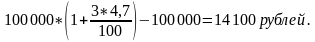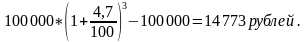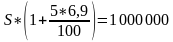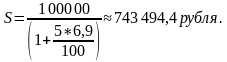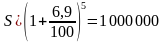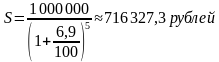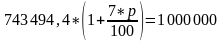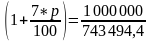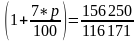сложные проценты в реальной жизни проектная работа 10 класс
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа № 42 им. Л.Н.Толстого
п. Лев Толстой Липецкой области
Проценты в жизненных ситуациях.
учащийся 10 «Б» класса
Руководитель учитель математики
Шуваева Елена Николаевна
Цель исследовательской работы.
История возникновения процента.
Сложные проценты-мощное оружее по увеличению капитала.
2.1.Сложные проценты и геометрическая прогрессия.
2.2.Формула сложных процентов для банковских вкладов.
2.3.Как выгодно вложить в сберегательный банк денежные средства.
3.Определение стоимости потребительского кредита.
3.1.Сложный процентный рост.
6.Список использованной литературы(библиография).
В мире науки и техники, где человечество стремительно несётся вперёд, просто необходимо уметь считать и высчитывать. Строительство, обучение, кредиты, скидки в магазинах, да и просто стоя у плиты дома – всюду приходится столкнуться с процентами. Умение производить процентные расчеты, необходимы каждому человеку. В газетах, по радио и телевидению, в транспорте и на работе обсуждаются повышение цен, зарплат, рост стоимости акций, снижение покупательной способности населения и т. п.. Добавим сюда объявления коммерческих банков, привлекающих деньги населения на различных условиях, сведения о доходах по акциям различных предприятий и фондов, об изменении процента банковского кредита и пр. Все это требует умения производить хотя бы несложные процентные расчеты для сравнения и выбора более выгодных условий.
Современная жизнь делает задачи на проценты актуальными, так как сфера практического приложения процентных расчетов расширяется.
Цель исследовательской работы :
показать, что сложный процент является мощным орудием по увеличению капитала на длительных промежутках времени;
2. определение стоимости потребительского кредита, методом сложных процентов, при выборе вида кредита и определении банка.
Узнать историю возникновения процентов;
Проанализировать вклады Сбербанка
Проблемный вопрос: как выгодно вложить в Сбербанк денежные средства?;
Сделать сравнительный анализ стоимости потребительского кредита по кредитным учреждениям. « Берешь чужые, а отдаешь свои…»
1.История возникновения процентов
Слово процент от латинского слова pro centum, что буквально означает «за сотню» или «со ста». То есть процентом называется сотая часть числа. Идея выражения частей целого постоянно в одних и тех же долях, вызванная практическими соображениями, родилась еще в древности у вавилонян. Ряд задач клинописных табличек посвящен исчислению процентов, однако вавилонские ростовщики считали не «со ста», а «с шестидесяти».
«Римляне брали с должника лихву (т. е. деньги сверх того, что дали в долг). При этом говорили: «На каждые 100 сестерциев долга заплатить 16 сестерциев лихвы».
От римлян проценты перешли к другим народам Европы. В Европе проценты появились на 1000 лет позже, их ввел бельгийский ученый Симон Стевин. В 1584г. он впервые опубликовал таблицу процентов.
Долгое время под процентами понимались исключительно прибыль или убыток на каждые сто рублей. Они применялись только в торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчетах, статистике, науке и технике. Введение процентов было удобным для определения содержания одного вещества в другом; в процентах стали измерять количественное изменение производства товара, рост и спад цен, рост денежного дохода и т.д.
Ныне процент – это частный вид десятичных дробей, сотая доля целого (принимаемого за единицу). Знак % происходит, как полагают, от итальянского слова cento (сто), которое в процентных расчетах часто писалось сокращенно cto. Отсюда путем дальнейшего упрощения в скорописи буква t превратилась в наклонную черту (/), возник современный символ для обозначения процента. В 1685г. в Париже была напечатана книга «Руководство по коммерческой арифметике», где по ошибке вместо сtо было набрано %. После этого знак %, получил всеобщее признание и до сих пор мы пользуемся этим значком процента.
Сами проценты не дают экономического развития, но их знание помогает в развитии практических способностей, а также умение решать экономические задачи. Обдуманное изучение процентов может способствовать развитию таких навыков как экономичность, расчетливость.
2.1. Сложные проценты и геометрическая прогрессия.
Геометрическая прогрессия (основные формулы):
– формулы суммы первых n членов геометрической прогрессии.
Рассмотрим задачу: Увеличение так называемого срочного вклада S производится на р процентов через t месяцев хранения. Найти величину вклада S n спустя nt (п 
N ) месяцев хранения в банке после неоднократного пролонгирования договора.
Решение. Согласно условию 
.
т.е. 
(формула сложных процентов).
2.2 Формула сложного процента для банковских вкладов
Формула сложного процента применительно к банковским вкладам несколько сложнее, чем описана выше.
Процентная ставка для вклада (%) рассчитывается так:
% = p * d / y
То есть можно рассчитывать процентную ставку для различных периодов вклада.
Формула сложного процента для банковских вкладов выглядит так:
При расчете сложных процентов нужно принимать во внимание тот факт, что со временем наращивание денег превращается в лавину. В этом привлекательность сложных процентов. Представьте себе маленький снежный комок размером с кулак, который начал катиться со снежной горы. Пока комок катится, снег налипает на него со всех сторон и к подножию прилетит огромный снежный камень. Также и со сложным процентом. Поначалу прибавка, создаваемая сложным процентом, почти незаметна. Но через какое-то время она показывает себя во всей красе. 
Расчет сложных процентов:
Рассмотрим 2 варианта:
1. Простой процент. Вы инвестировали 50 000 руб на 15 лет под 20%. Дополнительных взносов нет. Всю прибыль вы снимаете.
2. Сложный процент. Вы инвестировали 50 000 руб на 15 лет под 20%. Дополнительных взносов нет. Каждый год проценты прибыли прибавляются к основной сумме.
Начальная сумма: 50 000 рублей
Процентная ставка: 20% годовых
Таблица №1 (см. Приложение)
Вложения с использованием сложного процента выгоднее, чем с простым процентом. Чем больше проценты прибыли, чем дольше срок инвестирования, тем ярче проявляет себя сложный процент.
Вложения с использованием сложного процента выгоднее, чем с простым процентом. Чем больше проценты прибыли, чем дольше срок инвестирования, тем ярче проявляет себя сложный процент.
В случае простого процента график увеличения капитала получается линейный, поскольку вы снимаете прибыль и не даёте ей работать и приносить новую прибыль. В случае сложного процента график получается экспоненциальным, с течением времени кривая увеличения капитала становится всё круче, всё больше стремится вверх. Это происходит оттого, что из года в год прибыль накапливается и создаёт новую прибыль.
На графике ниже показано как вырастет капитал, если вложить 50 000 руб на 15 лет под 10%, 15% и 20%.
Таким образом, сложный процент является мощным орудием по увеличению капитала на длительных промежутках времени.
2.3.Как выгодно вложить в сберегательный банк денежные средства?
В настоящее время все вклады в банк (депозиты), производимые в целях сохранения и приумножения денег, то есть получения банковских процентов на вложенные средства, можно разделить на две категории:
По бессрочным вкладам (или вкладам до востребования) банки выплачивают крайне низкие проценты (обычно процентная ставка составляет 0,1% в год) или не выплачивают их вовсе. Низкое значение процентной ставки, отчасти связано с тем, что вклады до востребования не дают банкам возможности их размещения и использования в течение длительного времени. Кроме того, принимая вклады, банки берут на себя определенные риски: экономические, политические, юридические, инфляционные. А также затраты на содержание банковских сотрудников, юристов, налоговые службы.
Вторую группу депозитов образуют « срочные вклады « (вклады, которые банки принимают на фиксированный, заранее определенный срок). Такие вклады банки принимают обычно на период от 2, 3, 6 месяцев до 2-3 лет. В этом случае вкладчикам предлагается более высокий банковский процент (процентную ставку), как правило, зависящий от срока вклада и размера вложенных средств. Банки, таким образом, могут распоряжаться этими средствами в течение более длительного времени.
Следует отметить, что надежные банки, как правило, предоставляют невысокие проценты на депозиты своих клиентов.
Мы рассмотрели вклады Сбербанка «Сохраняй», «Пополняй», «Управляй».
Составили таблицу№2 (см. Приложение).
Из таблицы видно, что на процентную ставку по вкладу влияет сумма вклада, срок вклада, и его тип. Чем больше сумма вклада, дольше срок вклада, тем выше ставка. Еще одно правило: больше доходность у тех вкладов, которые лежат в банке без права снятия денежных средств. Видим из таблицы, что больше всего прибыли приносят вклады с выплатой процентов в конце срока, которые пролежат в банке 2-3 года.
Большая доходность получается у вкладов с капитализацией процентов, когда применяются сложные проценты.
3. Определение стоимости потребительского кредита
3.1 сложный процентный рост.
Уже в далекой древности было распространено ростовщичество – выдача денег по проценты. Разность между той суммой, которую возвращали ростовщику, и той, которую первоначально взяли у него, называли лихвой. Так, в Древнем Вавилоне она составляла 20 % и более! Это означало, что ремесленник, взявший у ростовщика 1000 денежных единиц сроком на год, возвращал ему по прошествии года на менее 1200 этих же единиц.
Известно, что в XIV–XV вв. в Западной Европе широко распространялись банки – учреждения, которые давали деньги в долг князьям, купцам, ремесленникам, финансировали дальние путешествия, завоевательные походы и т.д. Конечно, банки давали деньги не бескорыстно: за пользование предоставленными деньгами они брали плату, как и ростовщики древности. Эта плата выражалась обычно в виде процентов к величине выданных в долг денег.
Тех, кто берет в долг деньги в банке, называют заёмщиками, а ссуду, т.е. величину взятых у банка денег, называют кредитом. Основную часть тех денег, которые банки выдают заёмщикам, составляют деньги вкладчиков, которые они вносят в банк на хранение. Часть прибыли, которую получает банк, он передает вкладчикам в виде платы за пользование их деньгами. Эта плата также обычно выражается в процентах к величине вклада. Таким образом, средства, помещенные на хранение в банк, через определенный период времени приносят некоторый доход, равный сумме начисленных за этот период процентов.
Итак, с одной стороны, банки принимают вклады и платят по этим вкладам проценты вкладчикам, а с другой стороны – дают кредиты заёмщикам и получают от них проценты за пользование этими деньгами. Разность между той суммой, которую получает банк от заёмщиков за предоставленные кредиты, и той, которую он платит по вкладам, и составляет прибыль банка. Таким образом, банк является финансовым посредником между вкладчиками и заёмщиками
Нашу жизнь сейчас сложно представить без кредитов.
В настоящее время перед каждым человеком, который собирается брать кредит встает вопрос о цене кредита. Ежедневно мы видим рекламу о разных видах кредитов в газетах и журналах, на телевидении, транспорте; часто слышим о кредитах и по радио. Наслышаны о банках, которые выдают эти кредиты. Информации много и есть предложения, которые нам кажутся очень заманчивыми. Поэтому вопрос о стоимости кредита должен играть одну из главных ролей в выборе вида кредита и определении банка, с которым Вы хотели бы сотрудничать.
Деятельность банка требует постоянных затрат. Во всем мире основные деньги банки зарабатывают за счет разницы депозитов (вкладов) и ценной кредитов. Ставка по вкладам всегда ниже ставки по кредитам. Но существует мнение, что стоимость заемных денег складывается еще:
из инфляции и гонорара банку;
из стоимости программного обеспечения, позволяющего быстро обрабатывать огромную массу информации;
стоимости аренды помещений офисов банка, чтобы клиенту не приходилось искать банк за тридевять земель и стоять в очереди;
из зарплаты сотрудников, которые тратят рабочее время на оформление и обслуживание счета заемщика;
взносов в Агентство страхования вкладов.
Прежде чем говорить о стоимости кредита, надо рассмотреть такие понятия как: ежемесячные выплаты по процентам, единовременная комиссия и фиксированная комиссия. А после определения цены кредита следует еще обратить внимание на условия, в которых говорится о досрочном погашении кредита.
Приведем пример расчета ежемесячных выплат по процентам.
Допустим, был взят «Потребительский кредит» в сумме 30 000 рублей под 16,2% годовых на цели личного потребления на срок 36 месяцев, Сбербанке России. Кредит нужно погасить равными долями ежемесячно с одновременной уплатой процентов. Тогда процентная ставка в месяц будет равна 1,35%, но не от начальной суммы, а от той ее части, которая реально осталась у заемщика в текущий момент.
. Таблица №3 (Приложение).
На данном примере видим, что переплата за кредит составила 8081,86 рублей за 36 месяцев. Но в услуги Сбербанка входит страховка, которая составляет 1782,00рубля. Отсюда следует, что кредит взятый в Сбербанке России нам обошелся в 39873,86 рублей.
В наше время все чаще в наш обиход входят кредитные карты. Соблазна очень много: необходимые деньги можно снять в любое время, не надо стоять в очереди за кредитом, не нужно собирать документы и т.д. Но давайте рассмотрим, во что же нам обойдется взятый кредит.
При получении кредитной карты получили договор, в котором сказано, что, у нас кредитная карта на сумму 30 000 рублей. Срок кредита 36 месяцев. Процентная ставка по кредиту 19% годовых Минимальный ежемесячный платеж по погашению основного долга 10% от размера задолженности. Полная стоимость кредита 26,3% годовых. Длительность льготного периода 50дней, но нигде не сказано, что льготный период действует только тогда, когда оплата производится по безналичному расчету. Если снимать деньги по наличному расчету, то берется комиссия в размере 3%. Первый год обслуживания кредитной карты обходится бесплатно, за последующие два года берется по 750рублей.
Определим полную стоимость кредита:
d_i – дата i-го платежа;
d_0 – дата получения денег заемщиком или перечисления денег на счет продавца;
ДП_i – сумма осуществленных платежей (выданные средства вычитаются, платежи прибавляются), сюда включаются все дополнительные комиссии за рассмотрение заявки, открытие и ведение ссудного счета и т.д.
Полная стоимость кредита составит 26,3% годовых.
Мы рассмотрели два примера по кредитованию. В первом случае будет затрачено определенное количество времени, необходимо собрать документы для получения кредита. Во- втором случае все проще, но как мы видим полная стоимость кредита почти в 1,5 раза выше. Поэтому выбор у каждого индивидуальный и необходимо четко все рассчитать, чтобы не получилось вот так…
Исследовательский проект по математике «Сложные проценты в нашей жизни»
В рамках проектной технологии работаю в тесном сотрудничестве с учителями-предметниками. Поскольку учащиеся к середине 9 класса уже определились в своих предпочтениях, то им предлагаю выполнить проектную работу информационного, исследовательского, творческого характера в выбранной ими области. Некоторые работы были связаны с содержанием элективных курсов, другие стали результатом самостоятельного углубленного и дополнительного изучения материалов предметных курсов. Лучшие работы были представлены на школьных научных конференциях и региональных конференциях.
Просмотр содержимого документа
«Исследовательский проект по математике «Сложные проценты в нашей жизни»»
Тихонова Ольга Владимировна,
учитель математики МОУ-СОШ №9
города Аткарска саратовской области
В рамках проектной технологии работаю в тесном сотрудничестве с учителями-предметниками. Поскольку учащиеся к середине 9 класса уже определились в своих предпочтениях, то им предлагаю выполнить проектную работу информационного, исследовательского, творческого характера в выбранной ими области. Некоторые работы были связаны с содержанием элективных курсов, другие стали результатом самостоятельного углубленного и дополнительного изучения материалов предметных курсов. Лучшие работы были представлены на школьных научных конференциях и региональных конференциях.
Исследовательский проект по математике
«Сложные проценты в нашей жизни»
Данная работа несёт за собой значительную практическую значимость, которая в будущем поможет более разумно размещать свои средства. Данный проект могу рекомендовать учащимся 9-11 классов на математических кружках и занятиях по подготовке к ЕГЭ с целью подготовки к экзаменам при решении задач на проценты. А так же данная работа облегчит вкладчикам поиск более выгодных условий для вложения своих временно свободных средств, поможет разобраться в непростых финансовых механизмах и выбрать для себя оптимальную стратегию управления собственными денежными средствами.
Сложные проценты окружают нас в современной жизни, и в большей степени распространены в таких глобальных структурах, как банковская. В настоящее время банковская система играет значительную роль в экономике нашей страны. Процентные вычисления представляютинтерес не только для будущих финансистов, но и для каждого человека. Многие жизненные ситуации требуют знания вычисления процентов:
1. Получение кредитов в банке;
2. Банковские вклады;
3. Покупка товара в кредит;
4. Расчёт налогообложения.
Из выше перечисленных жизненных ситуаций я выбрала банковские вклады в качестве применения сложных процентов. Новизна исследования
состоит в том, что в работе рассматриваются сведения, которые не изучаются в школьном курсе математики и впервые тема обобщается на местном материале.
Сформировать понимание необходимости знаний процентных вычислений для решения большого круга задач;
Научиться применять знания о процентах в повседневной жизни;
Рассмотреть понятие сложных процентов;
Научиться решать задачи на сложные проценты;
Показать, что формула сложных процентов – это ни что иное,как геометрическая прогрессия;
Провести исследование пяти банков Аткарска и сделать вывод, куда наиболее выгодно вкладывать деньги.
Почему я решила выбрать именно эту тему для своего проекта:
Я уже делала проект на подобную тему в 8 классе: «Кредит. За и против», где я определила, в каких банках нашего города наиболее выгодно взять кредит на образование. Я решила продолжить свою работу над процентами и кредитами, но на этот раз я решила рассмотреть, в какой банк Аткарска выгоднее вкладывать деньги.Также, работа с процентами встречается в задаче номер 17 в ЕГЭ по профильной математике. Поэтому, я считаю, что данная тема будет актуальна также и среди будущих или нынешних одиннадцатиклассников.
2.1 История возникновения процентов:
Проценты – одно из математических понятий, которые часто встречаются в повседневной жизни.
Идея выражения частей целого постоянно в одних и тех же долях, вызванная практическими соображениями, родилась еще в древности у вавилонян, которые пользовались шестидесятеричными дробями. Уже в клинописных таблицах вавилонян содержатся задачи на расчет процентов. До нас дошли составленные вавилонянами таблицы процентов, которые позволяли быстро определить сумму процентных денег. Были известны проценты и в Индии. Индийские математики вычисляли проценты, применив так называемое тройное правило, т. е. пользуясь пропорцией. Они умели производить и более сложные вычисления с применением процентов. Денежные расчеты с процентами были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. Даже римский сенат вынужден был установить максимально допустимый процент, взимаемый с должника, так как некоторые заимодавцы усердствовали в получении процентных денег. От римлян проценты перешли к другим народам.
В средние века в Европе в связи с широким развитием торговли особо много внимания обращали на умение вычислять проценты. В то время приходилось рассчитывать не только проценты, но и проценты с процентов, т. е. сложные проценты, как называют их в наше время. Отдельные конторы и предприятия для облегчения труда при вычислениях процентов разрабатывали свои особые таблицы, которые составляли коммерческий секрет фирмы.
Впервые опубликовал таблицы для расчета процентов в 1584 году Симон Стевин – инженер из города Брюгге (Нидерланды). Стевин известен замечательным разнообразием научных открытий в том числе – особой записи десятичных дробей.
Долгое время под процентами понимались исключительно прибыль и убыток на каждые 100 рублей. Они применялись только в торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчетах, статистике, науке и технике. Нынче процент – это частный вид десятичных дробей, сотая доля целого (принимаемого за единицу).
2.2Понятия «простые проценты» и «сложные проценты»:
Простые проценты — метод расчета процентов, при котором начисления происходят на первоначальную сумму вклада (долга).
Простыми процентами можно считать вклад (долг) только в том случае, если происходит однократная выплата процентов и всей суммы вклада(долга) одновременно, при этом полностью отсутствует возможность досрочной частичной или полной выплаты вклада (долга) и/или полностью отсутствует возможность продления вклада (долга).
При досрочной выплате процентов происходит увеличение суммы вклада (долга), значит первоначальная сумма вклада (долга) изменилась, следовательно, применение простых процентов в этом случае бессмысленно, поскольку это уже не простые проценты, а сложные.
Сложные проценты – форма расчета дохода, основанная на присоединении к сумме долга начисленных, но невыплаченных процентов, начисление процентов на проценты, расчет процентов на два или большее число периодов, проводимый таким образом, что процент начисляется не только на исходную сумму, но и на процент, начисленный в предыдущем периоде. При расчетах применяют сложные дискретные проценты, начисляемые за фиксированные интервалы времени.
Для начисления процентов по вкладам (депозитам) и кредитам, применяются следующие формулы процентов:
Представьте себе, что вы открыли в банке вклад в сумме а р. под р% годовых на t лет. У вас есть две стратегии поведения: либо в конце каждого года хранения вклада снимать проценты по вкладу, т. е. полученную прибыль в размере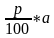 
рублей, либо прийти в банк один раз — в конце срока хранения вклада. Какой доход вы получите в том и другом случаях?
2.3 Формула простых процентов:
В первом случае при t = 1 вы получите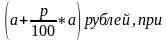 
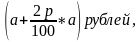
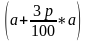
t = 2 ваша итоговая сумма составит 
при t = 3 – 
рублей и т. д. Математическая модель ситуации — конечная арифметическая прогрессия
Итак, при первой стратегии поведения за t лет вы получите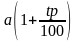 
р. — это так называемая фopмyла простых процентов.
2.4 Формула сложных процентов:
Если вы решили прийти в банк только в конце срока хранения вклада, то при t = 1 получаемая сумма составит, как и в первом случае,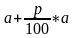 
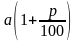
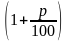
, т. е. 
р.; сумма вклада увеличилась в 
раз. Во столько же раз она увеличится и кконцу второго года хранения, и к концу третьего года хранения и т. д. Математическая модель ситуации — конечная геометрическая прогрессия
Итак, при второй стратегии поведения за t лет вы получите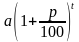 
р. — это так называемая формула сложных процентов.
Рассмотрим конкретный пример. Пусть вклад составляет 10 000 р., банк дает 10% годовых, срок хранения вклада — 5 лет. Если вы выбрали стратегию простых процентов, то к концу срока хранения вы получите в итоге сумму, равную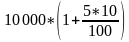 
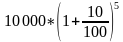
, т. е. 15 000 р. Если же вы выбрали стратегию сложных процентов, то к концу срока хранения вы получите в итоге сумму, равную 
, т. е. 16 105,1 р. Как говорится водном рекламном слогане, почувствуйте разницу
2.5 Исследование банковских вкладов:
Банковский вклад (или банковский депозит) — сумма денег, переданная лицом кредитному учреждению с целью получить доход в виде процентов, образующихся в ходе финансовых операций с вкладом.
Обычно банки предлагают простое начисление процентов. Что это значит? Это значит, что проценты будут начислены на ваш вклад только в конце срока. Т.е. допустим вы открыли вклад под 10% годовых и вложили 10 000 рублей. Через год вам будет начислено в виде процентов 1 000 рублей. Если вы оставите вклад на второй год, то по истечении этого срока вам будет начислена еще 1 000 рублей. За 2 года, при простом начислении процентов ваша итоговая сумма составит: 12 000 рублей.
Если бы было сложное начисление процентов, то картина немного меняется. Через 1 год, на вашем счету также было бы 11 000 рублей (10 000 — ваш вклад + 1 000 рублей в виде процентов). Однако, эта начисленная тысяча, в конце первого периода присоединилась бы к основному телу депозиту. И все проценты уже начислялись бы на эту общую сумму. Т.е. вы на второй год получили бы 10%, только уже не с 10 000 рублей, а с 11 тысяч. В деньгах это получается — 1 100 рублей. Итого, за 2 года при сложном начислении ваша сумма составит: 12 100 рублей
Я решила провести исследование, в какой из Аткарских банков выгоднее вкладывать деньги. Для этого я рассмотрела 5 банков: Сбербанк, ВТБ, Почта банк, Россельхозбанк и Совкомбанк.
Первоначальная сумма 100 000 рублей, срок – 3 года. Начисление процентов – ежегодное.
СБЕРБАНК (Саратовская область, г. Аткарск, ул. Советская,115)
= 100 000 рублей
= 3 года
= 4,24%
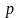
По формуле простых процентов доход составит:
По формуле сложных процентов доход составит:
ВТБ (Саратовская область, г. Аткарск, ул. Чапаева, 110)
= 100 000 рублей
= 3 года
= 5,09%
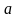
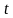
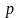
По формуле простых процентов доход составит:
По формуле сложных процентов доход составит:
СОВКОМБАНК (Саратовская область, г. Аткарск, ул. Коммунистическая,2)
= 100 000 рублей
= 3 года
= 6,9%
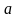
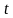
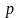
По формуле простых процентов доход составит:
По формуле сложных процентов доход составит:
РОССЕЛЬХОЗБАНК (Саратовская область, г. Аткарск, ул.Пушкина,87)
= 100 000 рублей = 3 года = 5,91%
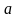
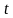
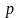
По формуле простых процентов доход составит:
По формуле сложных процентов доход составит:
ПОЧТА БАНК (Саратовская область, г. Аткарск, ул. Советская, 62)
= 100 000 рублей
= 3 года
= 4,7%
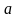
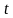
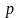
По формуле простых процентов доход составит:
По формуле сложных процентов доход составит:
Я пришла к выводу, что вклад выгоднее делать в Совкомбанке.
В следующем году я заканчиваю школу и у меня цель поступать в один из ВУЗов г. Саратова. Уже сейчас родители планируют приобрести мне собственную квартиру. Можно рассмотреть следующие варианты: приобретение вторичного жилья, квартира в новостройке или в строящемся доме. Стоимость жилья значительно отличается, поэтому мои родители выбирают самый выгодный вариант – приобретение жилья в новостройке. C 1 июля 2019 года принципиально трансформируется схема продаж жилья в строящихся домах: деньги дольщиков будут храниться в банке до ввода жилого комплекса в эксплуатацию. В конце прошлого года власти придумали новую схему финансирования жилищного строительства. Теперь девелоперы будут строить новое жилье только на кредиты банков или собственные деньги. Получать средства покупателей напрямую им нельзя.
Однако это не значит, что россияне потеряют возможность приобрести квартиру в строящемся доме, покупатель сможет выбрать понравившийся объект и заключить договор с застройщиком, но расплачиваться будет не с ним напрямую, а через банк, который выдал кредит на строительство.
Родители планируют приобрести квартиру в строящемся доме фирмы «N». Первоначальный взнос в момент закладки фундамента составляет 500 тыс. рублей. Я решила рассчитать, какую сумму нужно вложить в банк под 6,9% годовых, чтобы купить эту квартиру, если дом строится 5 лет, а стоимость квартиры по договору составляет 1,5 млн рублей?
Так как в практической жизни используются простые проценты, а задачи ЕГЭ решаются по формуле сложных процентов, то я провела расчеты по обеим формулам.
По формуле простых процентов сумма, которую нужно вложить в банк для того, чтобы по истечению 5 лет получить 1 млн рублей, составляет:
А по формуле сложных процентов:
Также, по формуле простых процентов рассчитаем процент, под который нужно вложить данную сумму на 7 лет, чтобы также получить 1 млн рублей:
И по формуле сложных процентов:
В процессе работы я исследовала простые и сложные проценты, а именно, рассмотрела понятие сложных процентов, провела анализ вкладов пяти банков Аткарска, научилась решать задачи на сложные проценты. Таким образом, цель моей работы достигнута.