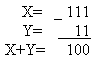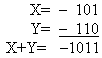сложение чисел в обратном и дополнительном кодах
Сложение чисел в обратном и дополнительном кодах
Арифметические операции на сумматорах прямого, обратного и дополнительного кода
Все операции в ЭВМ выполняют над числами, представленными специальными машинными кодами. Их использование позволяет обрабатывать знаковые разряды чисел так же, как и значащие разряды, а также заменять операцию вычитания операцией сложения.
Каждому двоичному числу можно поставить в соответствие несколько видов кодов.
Различают следующие коды двоичных чисел: прямой (П), обратный (ОК) и дополнительный (ДК).
Прямой код двоичного числа образуется из абсолютного значения этого числа и кода знака (0 или 1) перед его старшим числовым разрядом.
Прямой код двоичного числа образуется по следующему алгоритму:
1) определить данное двоичное число: либо целое (порядок), либо правильная дробь (мантисса);
2) если это дробь, то цифры после запятой можно рассматривать как целое число;
3) если это целое и положительное двоичное число, то вместе с добавлением нуля в старший разряд число превращается в код.
Для отрицательного двоичного числа перед ним ставится единица.
число Y 2 = +0,11011012 → код числа Y пр = 01101101.
Подчеркиванием выделяют знаковые разряды.
Обратный код двоичного числа образуется по следующему алгоритму:
1) обратный код положительных чисел совпадает с их прямым кодом;
2) обратный код отрицательного числа содержит единицу в знаковом разряде числа, а значащие разряды числа заменяются инверсными, т. е. нули заменяются единицами, а единицы нулями.
Свое название обратный код получил потому, что коды цифр отрицательного числа заменены инверсными.
Наиболее важные свойства обратного кода чисел:
— сложение положительного числа С с его отрицательным значением в обратном коде дает так называемую машинную единицу МЕок = 1|1111, состоящую из единиц в знаковом и в значащих разрядах числа;
— нуль в обратном коде имеет двоякое значение.
Он может быть как положительным числом 0|0000, так и отрицательным 1|1111.
Двойственное представление нуля явилось причиной того, что в современных ЭВМ все числа представляются не обратным, а дополнительным кодом.
Обратный код положительного двоичного числа совпадает с прямым кодом, а для отрицательного числа нужно, исключая знаковый разряд, во всех остальных разрядах нули заменить единицами и наоборот.
Дополнительный код положительных чисел совпадает с их прямым кодом. Дополнительный код отрицательного числа представляет собой результат суммирования обратного кода числа с единицей младшего разряда (2 0 – для целых чисел, 2 –k – для дробных).
Основные свойства дополнительного кода:
· сложение дополнительных кодов положительного числа С с его отрицательным значением дает так называемую машинную единицу дополнительного кода:
т. е. число 10 (два) в знаковых разрядах числа;
Дополнительный код положительного числа совпадает с его прямым кодом. Дополнительный код отрицательного числа образуется путем прибавления единицы к обратному коду.
Арифметические действия в машинных кодах
Сложение, а также вычитание чисел в обратном или дополнительном кодах выполняют с использованием обычного правила арифметического сложения многоразрядных чисел.
Это правило распространяется и на знаковые разряды чисел.
Различие обратного и дополнительного кодов связано с последующими действиями с единицей переноса из старшего разряда, изображающего знак числа.
При сложении чисел в обратном коде эту единицу надо прибавить к младшему разряду результата, а в дополнительном коде единица переноса из старшего разряда игнорируется, так как дополнительный код из обратного получается как раз прибавлением единицы.
Сложение и вычитание машинных чисел
Операция вычитания приводится к операции сложения путем преобразования чисел в обратный или дополнительный код согласно таблице.
Сложение (вычитание) машинных чисел
Скобки в представленных выражениях указывают на замену операции вычитания операцией сложения с обратным или дополнительным кодом соответствующего числа.
Сложение двоичных чисел осуществляется последовательно, поразрядно в соответствии с таблицей.
При выполнении сложения цифр необходимо соблюдать следующий алгоритм:
1) слагаемые должны иметь одинаковое число разрядов.
Для выравнивания разрядной сетки слагаемых можно дописывать незначащие нули слева к целой части числа и незначащие нули справа к дробной части числа;
2) знаковые разряды участвуют в сложении так же, как и значащие;
3) необходимые преобразования кодов производят с изменением знаков чисел. Приписанные незначащие нули изменяют свое значение при преобразованиях по общему правилу;
4) при преобразовании единицы переноса из старшего знакового разряда, в случае использования ОК, эта единица складывается с младшим числовым разрядом.
При использовании ДК единица переноса теряется. Знак результата формируется автоматически, результат представляется в том коде, в котором представлены исходные слагаемые.
1. Сложить два числа: А10 = 7, В10 = 16.
Исходные числа имеют различную разрядность, необходимо провести выравнивание разрядной сетки:
Сложение в обратном или дополнительном коде дает один и тот же результат:
2. Сложить два числа: А10 = +16, В10 = –7 в ОК и ДК.
По таблице необходимо преобразование А +(–В), в которой второй член преобразуется с учетом знака:
При сложении чисел в ОК и ДК были получены переносы в знаковый разряд и из знакового разряда.
В случае ОК перенос из знакового разряда требует дополнительного прибавления единицы младшего разряда.
В случае ДК этот перенос игнорируется.
Пример сложения чисел +18 и –7 приведен в таблице.
Обратный и дополнительный коды двоичных чисел



Пример перевода
x1=10101-[x1]пр=010101
x2=-11101-[x2]пр=111101
x3=0,101-[x3]пр=0,101
x4=-0,111-[x4]пр=1,111
2) Обратный код числа, используется для выполнения арифметических операций вычитания, умножения, деления, через сложение. Обратный код положительного числа совпадает с его прямым кодом, обратный код отрицательного числа формируется по правилам: в знаковом разряде записывается “1”; цифровые значения меняются на противоположные.
3) Дополнительный код числа, имеет такое же назначение, как и обратный код числа. Формируется по следующим правилам: положительные числа в дополнительном коде выглядят также как и в обратном и в прямом коде, т.е. не изменяются. Отрицательные числа кодируются следующим образом: к обратному коду отрицательного числа (к младшему разряду) добавляется 1, по правилу двоичной арифметики.
Пример перевода
x1=10101-[x1]доп=010101
x2=-11101-[x2]обр=100010+1-[x2]доп=100011
x3=0,101-[x3]доп=0,101
x4=-0,111-[x4]обр=1,000+1-[x4]доп=1,001
Для выявления ошибок при выполнении арифметических операций используются также модифицированные коды: модифицированный прямой; модифицированный обратный; модифицированный дополнительный, для которых под код знака числа отводится два разряда, т.е. “+”=00; ”-”=11. Если в результате выполнения операции в знаковом разряде появляется комбинация 10 или 01 то для машины это признак ошибки, если 00 или 11 то результат верный.
Особенности сложения чисел в обратном и дополнительном кодах.
При сложении чисел в дополнительном коде возникающая единица переноса в знаковом разряде отбрасывается.
При сложении чисел в обратном коде возникающая единица переноса в знаковом разряде прибавляется к младшему разряду суммы кодов.
Если результат арифметических действий является кодом отрицательного числа, необходимо преобразовать его в прямой код. При этом обратный код преобразуется в прямой заменой цифр во всех разрядах кроме знакового на противоположные. Дополнительный код преобразуется в прямой также, как и обратный, с последующим прибавлением единицы к младшему разряду.
Сложить двоичные числа X и Y в обратном и дополнительном кодах.
1) Сложим числа, пользуясь правилами двоичной арифметики:
2) Сложим числа, используя коды:
| Прямой код | Сложение в обратном коде | Сложение в дополнительном коде |
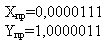 | 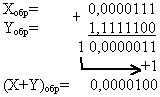 | 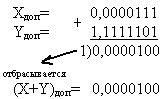 |
Так как результат сложения является кодом положительного числа (знак 0), то (X+Y)обр=(X+Y)доп=(X+Y)пр.
1) Сложим числа, пользуясь правилами двоичной арифметики:
2) Сложим числа, используя коды:
| Прямой код | Сложение в обратном коде | Сложение в дополнительном коде |
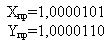 | 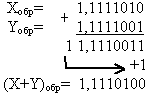 | 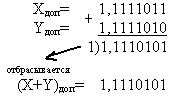 |
Так как сумма является кодом отрицательного числа (знак 1), то необходимо перевести результаты в прямой код:
(X+Y)обр=1,1110100 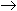
— из дополнительного кода
(X+Y)доп=1,1110101 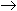
Дата добавления: 2015-08-01 ; просмотров: 2920 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Сложение чисел в обратном и дополнительном кодах
В большинстве компьютеров операция вычитания не используется. Вместо нее производится сложение обратных или дополнительных кодов уменьшаемого и вычитаемого. Это позволяет существенно упростить конструкцию АЛУ.
Сложение обратных кодов. Здесь при сложении чисел А и В имеют место четыре основных и два особых случая:
1. А и В положительные. При суммировании складываются все разряды, включая разряд знака. Так как знаковые разряды положительных слагаемых равны нулю, разряд знака суммы тоже равен нулю. Например:
Получен правильный результат.
2. А положительное, B отрицательное и по абсолютной величине больше, чем А. Например:
3. А положительное, B отрицательное и по абсолютной величине меньше, чем А. Например:
Компьютер исправляет полученный первоначально неправильный результат (6 вместо 7) переносом единицы из знакового разряда в младший разряд суммы.
4. А и В отрицательные. Например:
При сложении может возникнуть ситуация, когда старшие разряды результата операции не помещаются в отведенной для него области памяти. Такая ситуация называется переполнением разрядной сетки формата числа. Для обнаружения переполнения и оповещения о возникшей ошибке в компьютере используются специальные средства. Ниже приведены два возможных случая переполнения.
Сложение дополнительных кодов. Здесь также имеют место рассмотренные выше шесть случаев:
1. А и В положительные. Здесь нет отличий от случая 1, рассмотренного для обратного кода.
2. А положительное, B отрицательное и по абсолютной величине больше, чем А. Например:
3. А положительное, B отрицательное и по абсолютной величине меньше, чем А. Например:
Получен правильный результат. Единицу переноса из знакового разряда компьютер отбрасывает.
4. А и В отрицательные. Например:
Получен правильный результат в дополнительном коде. Единицу переноса из знакового разряда компьютер отбрасывает.
Случаи переполнения для дополнительных кодов рассматриваются по аналогии со случаями 5 и 6 для обратных кодов.
Деление для компьютера является трудной операцией. Обычно оно реализуется путем многократного прибавления к делимому дополнительного кода делителя.
Особенности сложения чисел в обратном и дополнительном кодах.
При сложении чисел в дополнительном коде возникающая единица переноса в знаковом разряде отбрасывается.
При сложении чисел в обратном коде возникающая единица переноса в знаковом разряде прибавляется к младшему разряду суммы кодов.
Если результат арифметических действий является кодом отрицательного числа, необходимо преобразовать его в прямой код. При этом обратный код преобразуется в прямой заменой цифр во всех разрядах кроме знакового на противоположные. Дополнительный код преобразуется в прямой также, как и обратный, с последующим прибавлением единицы к младшему разряду.
Сложить двоичные числа X и Y в обратном и дополнительном кодах.
1) Сложим числа, пользуясь правилами двоичной арифметики:
2) Сложим числа, используя коды:
| Прямой код | Сложение в обратном коде | Сложение в дополнительном коде |
 |  |  |
Так как результат сложения является кодом положительного числа (знак 0), то (X+Y)обр=(X+Y)доп=(X+Y)пр.
1) Сложим числа, пользуясь правилами двоичной арифметики:
2) Сложим числа, используя коды:
| Прямой код | Сложение в обратном коде | Сложение в дополнительном коде |
 |  |  |
Порядок выполнения работы:
1. Запишите дополнительный код числа, интерпретируя его как восьмибитовое целое со знаком
2. Запишите в десятичной системе счисления целое число, если дан его дополнительный код
3. Выполнить операции +,- чисел в обратных кодах
4. Выполнить операции +,- чисел в дополнительных кодах
1. Дайте определение понятию «дополнительный код»
2. Дайте определение понятию «обратный код»
3. Как реализовать операцию вычитания, с помощью операции сложения?
Практическая работа №2
Тема: Выполнение арифметических операций в естественной и нормальной форме
Цель работы: Научиться производить операции сложения и вычитания в дополнительных и обратных кодах
1. Калабеков Б.А. Цифровые устройства и микропроцессорные системы. – М.: Горячая линия, 2005г
2. Калиш Г.Г. Основы вычислительной техники. – М. Высш. шк., 2000 г.
Краткие теоретические сведения:
Числа с фиксированной точкой.
Запись числа с фиксированной точкой обычно имеет знаковый и цифровой разряды. Фиксированная точка означает, что на этапе конструирования ЭВМ было определено, сколько и какие разряды машинного слова отведены под изображение целой и дробной частей числа. Пример.
Как частный случай числа с фиксированной точкой может быть рассмотрена запись целого числа (в этом случае все разряды, кроме знакового, используются для записи целой части).
Пример.
Ячейка с записью целого числа.
Числа с плавающей точкой.
Для представления чисел с плавающей точкой (ЧПТ) используется полулогарифмическая форма записи числа:
Положение точки определяется значением порядка p. С изменением порядка точка перемещается (плавает) влево или вправо.
Пример.
12510=12.5*10 1 =1.25*10 2 =0.125*10 3 =0.0125*10 4 =.
Для установления однозначности при записи чисел принята нормализованная форма записи числа. Мантисса нормализованного числа может изменяться в диапазоне: 1/q ≤ | m | 10
Максимальным числом представимым в формате слова будет A=(0.1111. 1·10 1111111 )2 
Дата добавления: 2019-09-13 ; просмотров: 271 ; Мы поможем в написании вашей работы!