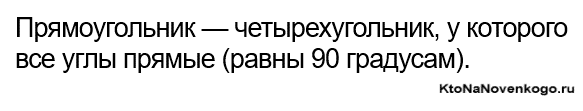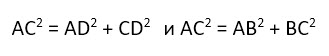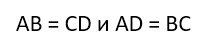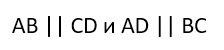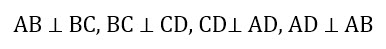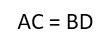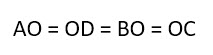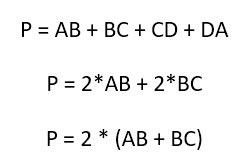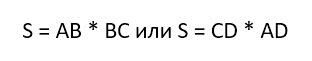Прямоугольник что это 2 класс
Урок математики по теме «Прямоугольник». 2-й класс
Класс: 2
Тип урока: открытие новых знаний.
Форма урока: урок-путешествие.
Оборудование: Презентация, электронное приложение к учебнику, карточки с заданиями и геометрические фигуры на доске и у учащихся.
I. Организационный момент
– Ребята, какое у вас настроение? Поделитесь своим настроением друг с другом. Поприветствуйте гостей.
II. Создание ситуации успеха
– Девиз сегодняшнего урока: ( слайд № 2)
Не говори: «Не могу».
Говори: «Надо научиться!»
– Я надеюсь, что этот урок даст вам новые знания из области математики.
– Сядьте за партой правильно:
Ноги под партой, руки у края.
Тетрадь под наклоном.
Спинка прямая.
– Ребята, а вы любите путешествовать?
В путешествие, друзья,
Приглашаю вас я.
И с собой прошу вас взять
Ручку, карандаш, тетрадь.
В пути вам нужно быть внимательными,
Наблюдательными и старательными.
– А куда мы с вами отправимся вы узнаете выполнив следующее задание.
III. Актуализация знаний
Устный счёт. (слайды № 3-11)
IV. Постановка учебной задачи
– Итак, мы отправляемся в страну Геометрию. (слайд № 12)
– А что такое – геометрия? (слайд № 13)
В переводе с греческого языка это слово означает «землемерие» ( «гео» – земля, «метрио» – измерять.) Геометрия зародилась в глубокой древности ( слайд № 14). Строя жилища и храмы, украшая их орнаментами, человек применял свои знания о форме, размерах и взаимном расположении предметов. Из геометрии вышла наука, которая называется математикой.
– Посмотрите, а вот и первый город. (слайд № 15). Называется он город Многоугольников. Но ворота закрыты.Чтобы открыть ворота нужно отгадать загадки, которые придумали жители этого города.
2. Об этой фигуре разносится весть: конца в ней пусть нет, начало – то есть. ЛУЧ
3. Хоть сто лет по ней идти,
Не найти конца пути. ПРЯМАЯ ЛИНИЯ
4. Хоть тоже без начала и конца,
Но я могу вилять туда – сюда. КРИВАЯ ЛИНИЯ
5. Часть прямой, ограниченная с двух сторон точками. ОТРЕЗОК
7. Кусок проволоки возьми
И его ты перегни.
Хочешь раз, а хочешь – два, Хочешь – три, четыре.
Что же получилось?
Что же появилось?
Не прямая, не кривая! ЛОМАНАЯ ЛИНИЯ!
– Попробуем теперь открыть ворота. А вот и ключик от замка.(слайд 16) Получилось. Мы входим в город и попадаем на «Площадь геометрических фигур».(слайд 17)
На доске многоугольники
– Назовите, какие фигуры видите.? Как их можно разделить на группы? (По количеству углов).
– Уберите шестиугольники (выходит один уч-ся).
– Какие группы фигур остались? ( Треугольники и четырёхугольники).
– Сколько треугольников? (2).
– Какой из них имеет прямой угол? Какой инструмент нам поможет это доказать? (Угольник.)
(Один уч-ся выходит к доске и показывает прямой угол в треугольнике).
– Уберём треугольники. Какие фигуры остались? (Четырёхугольники.)
– Какие углы имеют оставшиеся фигуры? (Уч-ся у доски определяет виды углов, используя угольник).
– Можно ли все эти фигуры назвать прямоугольниками? А как вы думаете, какой четырёхугольник называется прямоугольником?
– Назовите тему урока. (Прямоугольник.)
– Какую цель вы поставите перед собой? (Узнать. Какая фигура называется прямоугольником.)
V. Усвоение новых знаний
1. Сказка о прямоугольниках.
– В стране Геометрии есть остров (слайд 18). На острове живет очень важная фигура. (Слайд 19). Важность её признавалась всеми жителями острова. При изготовлении многих вещей форма её служила образцом. Кого бы ни встретила фигура на своём пути, всем хвасталась: «Посмотрите, какой у меня красивый вид: стороны все мои равны, углы все прямые, красивее меня нет фигуры на свете!»
– Как же тебя зовут, брат? – спрашивали все встречные.
– Ребята, а вы знаете, как называется эта фигура? (Квадрат.)
– А как вы узнали? (Стороны равны, углы прямые.)
Ходил квадрат по свету и стало тяготить его одиночество: ни побеседовать, ни потрудиться в хорошей и дружной компании. А уж какое веселье одному? Весело бывает только с друзьями. И решил квадрат поискать родственников. «Если встречу родственника, то я сразу его узнаю, – думал Квадрат, – ведь он на меня должен быть чем-то похож».
Однажды встречает он на пути такую фигуру (слайд 20)
Стал Квадрат к ней приглядываться. Что-то знакомое, родное увидел он в этой фигуре.
– Вы не догадались, ребята, чем похожи эти фигуры? (Все углы прямые.)
И спросил тогда Квадрат: «Как зовут тебя?»
– Меня зовут…
– Кто знает, как называется эта фигура? (Прямоугольник.)
– Правильно, прямоугольник. А почему же она так называется? (Все углы прямые.)
– Давайте убедимся в этом. При помощи треугольника измерим все углы. (Работа с прямоугольниками на местах, один уч-ся у доски.)
– Сколько сторон у прямоугольника? (4)
– Покажите стороны, которые лежат одна против другой. Это противоположные стороны.
– Измерьте их длину. Что скажете? (Они равны.)
– Измерьте две другие противоположные стороны.(Они равны.)
– Сформулируйте вывод о длине противоположных сторон прямоугольника. (Противоположные стороны прямоугольника равны.)
– В этом можно также убедиться, не измеряя стороны, а накладывая их друг на друга.
– Вот квадрат и спрашивает: «А мы не родственники с тобой?»
«Я бы тоже рад был узнать об этом, – отвечает Прямоугольник. – Если у нас найдутся четыре признака, по которым мы похожи, значит мы с тобой близкие родственники и у нас одна и та же фамилия.
Стали они искать и нашли эти четыре признака сходства.
– Давайте и мы их найдём. (1.Четыре угла. 2. Все углы прямые. 3. Четыре стороны. 4. Противоположные стороны равны.)
– Молодцы, ребята! А какая же общая фамилии может быть у этих фигур? (Прямоугольники)(слайд 21)
– Давайте проверим, правы ли мы.
Чтение правила в учебнике на с.14
– Обрадовались Квадрат и Прямоугольник тому, что нашли близких родственников, и стали с тех пор дружить.
– Понравилась сказка? О какой новой дружбе вы узнали?
2. Работа с электронным приложением к учебнику.
VI. Первичная проверка знаний
1. Работа с учебником.
Выполнение задания № 1 на с. 14.
– Найдите четырёхугольники у которых все углы прямые. Назовите номера этих фигур.
– Осмотрите нашу классную комнату. Назовите предметы, прямоугольной формы.
Выполнение задания № 2 на с. 14
– Сколько фигур вы раскрасили? (1)
VII. Закрепление изученного материала
1. Работа по учебнику
– Прочитайте условие задачи.
– Поставьте вопрос так, чтобы она решалась в одно действие, в два действия. Решите составную задачу.
№ 5 (с. 14)
– Рассмотрите числовые выражения. Можно ли поставить между ними знаки сравнения, не вычисляя значения выражений?
2. Работа в тетради с печатной основой
№ 40 (с.15) Самостоятельное выполнение.
Проверка по эталону (слайд 22)
– Обменяйтесь тетрадями. Оцените работу товарища.
VIII. Рефлексия (слайд 23)
IX. Подведение итогов
– Что нового узнали сегодня на уроке?
– Что осталось непонятным?
– Какое задание было трудно выполнять?
Домашнее задание: № 3, 6 с.14 (При решении задачи обратить внимание на выбор числа, обозначающего количество денег.)
Используемая литература: Ситникова Т.Н., Яценко И.Ф. «Поурочные разработки по математике: 2 класс» М.: ВАКО, 2012.
Урок геометрии во 2-м классе по теме: «Виды четырехугольников. Прямоугольник»
Тема: Виды четырехугольников. Прямоугольник
Тип урока – комбинированный.
Вид урока – дидактическая игра.
Методы и приемы обучения: диалогический и эвристический методы:
Ход урока
Сегодня на уроке мы с вами совершим путешествие в удивительную страну Геометрию:
– Кто знает, что в переводе с греческого обозначает слово “геометрия”?
“Гео” – земля, “метрия” – измерение.
Наука эта появилась в Греции.
Сопровождать нас будет в нашем путешествии (учитель показывает сказочного героя) удивительный герой – волшебник.
– Всех вас он зашифровал, и вы будете путешествовать под зашифрованными номерами.
– Кто узнал его? (Старик Хоттабыч.)
– Кто написал книжку “Старик Хоттабыч”? (Лагин.)
Старик Хоттабыч очень старый волшебник и его знания устарели, поэтому он пришел к вам на урок и хочет узнать, что же сейчас изучают современные дети. Помогите волшебнику разобраться.
– Что изображено на доске? (Геометрические фигуры.)
– Определите на какие 2 группы вы могли бы разделить эти геометрические фигуры? (Треугольники и четырехугольники.)
Заполните карточку №1. Укажите номера треугольников и четырехугольников. Все дети указывают в карточке номера.
В это время 2 ученика фиксируют ответы на доске.
– Укажите во второй карточке номера треугольников по углам (тупоугольный, прямоугольный, остроугольный) и по сторонам (равносторонний и равнобедренный).
Работу выполняют по вариантам, а потом обмениваются карточками и осуществляют взаимопроверку в парах.
ников
1 10
Стороны треугольника
ников
1) Сегодня мы с нашим героем познакомимся с видами четырёхугольников, а именно; с прямоугольником, научимся его чертить и выделять среди других фигур Т.к. треугольников и четырёхугольников в геометрии много. Вот как выглядят некоторые из них:
– Какие из них вы уже знаете?
Дети называют те виды, которые знают.
– Что общего у этих фигур, что их объединяет в одну группу?
(4 стороны, 4 угла, 4 вершины.)
– А чем один вид отличается от другого? (Длинами сторон и особенностями углов.)
Учитель обращает внимание детей на таблицу и говорит определения.
2) Помогите Хоттабычу из ряда четырехугольников найти похожие (1 3 5).
– Как называются углы у фигур 1, 3, 5? (Прямые.)
– А как бы вы назвали эти фигуры? (Прямоугольники.)
– Попробуйте сказать, что же такое прямоугольник?
Прямоугольник – геометрическая фигура, у которой все углы прямые и противоположные стороны равны.
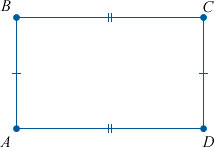
– Назовите вершины у прямоугольника АВСД? (А, В, С, Д – вершины.)
Что такое прямоугольник: определение, свойства, признаки, формулы
В данной публикации мы рассмотрим определение, свойства и признаки одной из основных геометрических фигур – прямоугольника. Также приведем формулы, с помощью которых можно найти его площадь и периметр.
Определение прямоугольника
Прямоугольник – это четырехугольник, у которого все углы равны 90° (т.е. являются прямыми).
∠ABC = ∠BCD = ∠BAD = ADC = 90°
Прямоугольник состоит из:
Сам прямоугольник обычно записывается путем перечисления его вершин, например, ABCD в нашем случае.
Примечание: Прямоугольник является разновидностью параллелограмма.
Свойства прямоугольника
Свойство 1
Противоположные стороны прямоугольника попарно параллельны и равны.
Свойство 2
Длина и ширина прямоугольника одновременно являются его высотами, т.к. они взаимно перпендикулярны.
Свойство 3
Если соединить середины сторон прямоугольника, то получится ромб.
Свойство 4
Квадрат диагонали (d) прямоугольника равняется сумме квадратов его смежных сторон.
d 2 = a 2 + b 2
Это следует из теоремы Пифагора, которую можно применить к любому из прямоугольных треугольников, которые образуются в результате деления диагональю прямоугольника.
Свойство 5
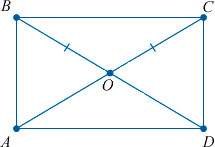
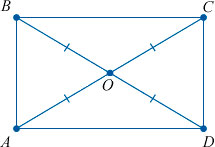
Диагонали прямоугольника равны, и в точке пересечения делятся пополам.
Свойство 6
Около любого прямоугольника можно описать окружность, радиус (R) которой равен половине диагонали этого прямоугольника.
Следовательно, диаметр окружности равен полной длине диагонали прямоугольника.
Признаки прямоугольника
Параллелограмм является прямоугольником, если верно одно из следующих утверждений:
Формулы
1. Площадь прямоугольника (S):
2. Периметр прямоугольника (P):
Прямоугольник — это одна из основ геометрии
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы расскажем об одной из основных геометрических фигур – ПРЯМОУГОЛЬНИКЕ.
Название это весьма говорящее, и в нем скрыто официальное определение.
Прямоугольник – это четырехугольник, у которого все углы прямые, то есть равны 90 градусам.
Впервые описание этой фигуры встречается еще в Древнем Египте. Но в те времена все геометрические правила давались как неопровержимые истины, не предоставляя доказательств.
Более правильный подход появился в Древней Греции. И естественно, автором стал самый знаменитый математик той эпохи — Евклид. А прямоугольник, как и многие другие фигуры и термины, был подробно описан в его произведении «Начала».
Прямоугольник — это.
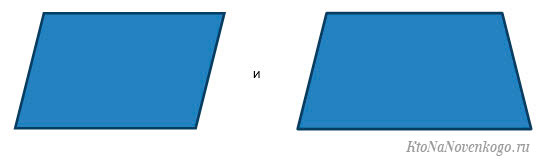
Все тот же Евклид разделил все четырехугольники на два вида – параллелограммы (что это?) и трапеции (что это?).
У первых противоположные стороны равны и параллельны, а у вторых параллельна только одна пара сторон, и они при этом не равны.
То есть выглядит это так:
Так вот, прямоугольник в данном случае является частным случаем параллелограмма.
У этой фигуры противоположные стороны параллельны. Это первое условие по Евклиду. И к тому же они равны, что является условием номер два.
У прямоугольника есть и собственный частный случай. Когда равны не только противоположные стороны, а все. И как нетрудно догадаться, фигура эта называется квадрат.
Ну, и логично предположить, что квадрат (как и сам прямоугольник) является частным случаем параллелограмма.
Признаки прямоугольника
Признаки геометрической фигуры – это совокупность отличий, по которым ее можно выделить среди других.
В случае с прямоугольником их всего три:
Диагонали прямоугольника
Как мы уже упомянули выше, диагонали прямоугольника (отрезки, соединяющие его противоположные углы) равны между собой.
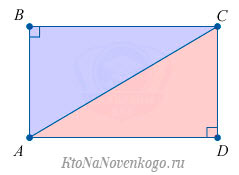
Доказать это можно с помощью известной теоремы Пифагора. Она гласит, что «Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы».
В нашем случае гипотенузой является диагональ прямоугольника, которая делит его на два равных прямоугольных треугольника. И теорема Пифагора выглядит следующим образом:
Свойства прямоугольника
К свойствам прямоугольника относятся следующие утверждения:
Периметр и площадь
Для того чтобы определить периметр прямоугольника, надо просто сложить длины всех его четырех сторон.
Но с учетом того, что попарно они равны, то конечная формула может выглядеть более просто:
Площадь прямоугольника вычисляется также весьма просто. Надо лишь перемножить две его стороны:
К слову, это не единственная формула для вычисления площади. Площадь также можно получить, имея значение периметра фигуры или длину его диагонали. Но эти формулы гораздо сложнее.
Вот и все, что мы хотели рассказать о геометрической фигуре ПРЯМОУГОЛЬНИК. До новых встреч на страницах нашего блога.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (5)
Главная основа геометрии — это все же треугольник. Через него можно построить любую фигуру и доказать любую теорему.
Не согласен с утверждением, что раз один угол прямой, то перед нами точно прямоугольник, всё же прямоугольник — это когда все противоположные стороны параллельны друг другу, а если только один угол прямой, то там и трапеция может быть.
Я бы сказала, что прямоугольник — это основа архитектуры. Все здания так или иначе используют эту фигуру в своем дизайне.
Вот за что я люблю прямоугольники, так за то, что площадь его легко найти, да и периметр, вот с трапецией сложнее, увы, но те же земельные участки больше трапеции, отсюда и земельные споры.
Урок математики для 2 класса «Прямоугольник и его свойства»
План-конспект урока (2 класс) учитель начальных классов МОУ СШ № 128 Красильникова Людмила Михайловна
Предметная область : математика
Тип урока : урок получения новых знаний
Цель: Создать условия для ознакомления учащихся со свойствами прямоугольника и применение знаний на практике.
Сформировать четкое представление о прямоугольнике;
Организовать исследовательскую деятельность по определению свойств прямоугольника;
Определение понятия «прямоугольник»;
Внешний вид прямоугольника;
Характеристику прямоугольника: длина и ширина;
Алгоритм построения прямоугольник;
Правила измерения длины и ширины;
Распознавать прямоугольник среди других геометрических фигур;
Распознавать объекты, формы которых содержат прямоугольник в реальной жизни;
Отличать прямоугольник от других четырехугольников;
Объяснять разницу между прямоугольником и ромбом, прямоугольником и трапецией;
Отличать длину и ширину;
Находить и измерять длину и ширину;
Называть свойства прямоугольника;
Строить прямоугольник на листе;
Объяснять разницу между двумя прямоугольниками.
Самостоятельно определять и высказывать самые простые, общие для всех людей правила поведения при совместной работе и сотрудничестве, самостоятельно делать выбор, какой поступок совершить.
Определять цель деятельности на уроке с помощью учителя и самостоятельно; учиться совместно с учителем и формулировать учебную проблему, планировать учебную деятельность на уроке; высказывать свою версию, пытаться предлагать способ её проверки, работая по предложенному плану, использовать необходимые средства (учебник, простейшие приборы и инструменты); определять успешность выполнения своего знания в диалоге с учителем.
ориентироваться в своей системе знаний: понимать, что нужна дополнительная информация (знания), для решения учебной задачи в один шаг; делать предварительный отбор источников информации для решения учебной задачи; добывать новые знания, извлекать информацию, представленную в разных формах (текст, таблица, схема, иллюстрация и др.); перерабатывать полученную информацию: наблюдать и делать самостоятельные выводы.
участвовать в диалоге на уроке; отвечать на вопросы учителя, товарищей по классу;
слушать и понимать речь других; взаимодействовать в паре.