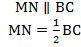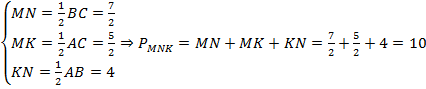Прямая проходит через середины двух сторон треугольника докажите что высоты
Прямая проходит через середины двух сторон треугольника докажите что высоты
Докажите, что расстояние от вершины треугольника до точки пересечения высот вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.
Решение
Четвёртый способ. Из равенства (см. задачу 55367) следует, что
Пятый способ. Пусть A1 – точка, диаметрально противоположная вершине A. Тогда ∠ABA1 = ∠ACA1 = 90°, а так как BH ⊥ AC и CH ⊥ AB, то BH || CA и
CH || BA1. Значит, BHCA1 – параллелограмм. Его диагонали делятся точкой пересечения K пополам. При этом OK ⊥ BC. Отрезок OK – средняя линия треугольника AHA1, следовательно, OK = AH /2.
Шестой способ. Пусть L и F – середины отрезков AC и CH соответственно. Тогда OK ⊥ BC и AH ⊥ BC, поэтому OK || AH. С другой стороны, LF – средняя линия треугольника AHC, поэтому LF || AH и LF = AH /2. Следовательно, LF || OK. Отрезок KF – средняя линия треугольника BHC, поэтому KF || BH, а так как BH ⊥ AC, то KF ⊥ AC. С другой стороны, OL ⊥ AC, значит, OL || KF. Противоположные стороны четырёхугольника OKFL попарно параллельны, значит, это параллелограмм. Следовательно, OK = LF = AH /2.
Источники и прецеденты использования
| web-сайт | |
| Название | Система задач по геометрии Р.К.Гордина |
| URL | http://zadachi.mccme.ru |
| задача | |
| Номер | 1257 |
Как найти среднюю линию треугольника?
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Понятие треугольника
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.
Треугольник, у которого все стороны равны, называется равносторонним или правильным.
Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты.
Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.
Свойства треугольников:
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Понятие средней линии треугольника
Определение средней линии треугольника подходит для любого вида этой фигуры.
Средняя линия треугольника — отрезок, который соединяет середины двух сторон. В любом треугольнике можно провести три средних линии.
Основанием считается сторона, которой параллельна средняя линия.
Как найти среднюю линию треугольника — расскажем дальше, а для начала еще немного разберемся со всеми определениями.
Понятие средней линии прямоугольного треугольника
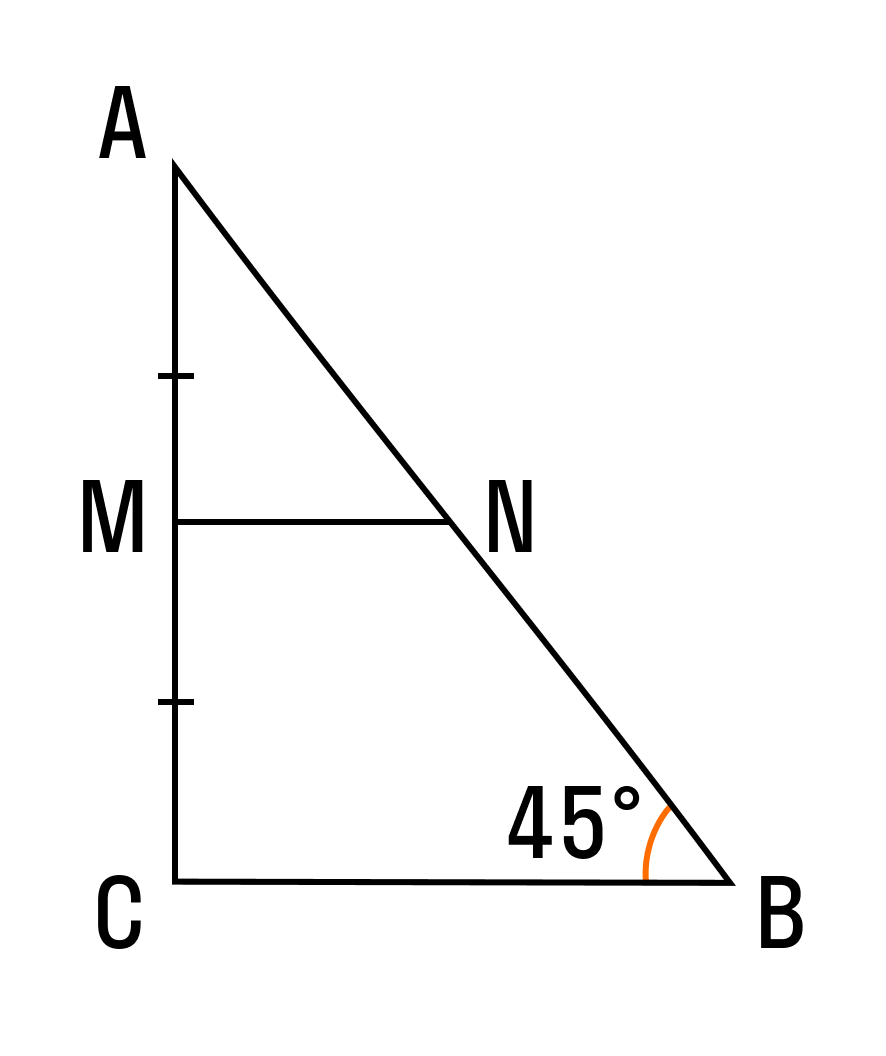
Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.
Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.
В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.
Свойства средней линии треугольника
Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.
Свойства:
Теорема о средней линии треугольника
Теорема о средней линии треугольника звучит так:
Средняя линия треугольника параллельна основанию и равна его половине. А так выглядит формула нахождения средней линии треугольника:
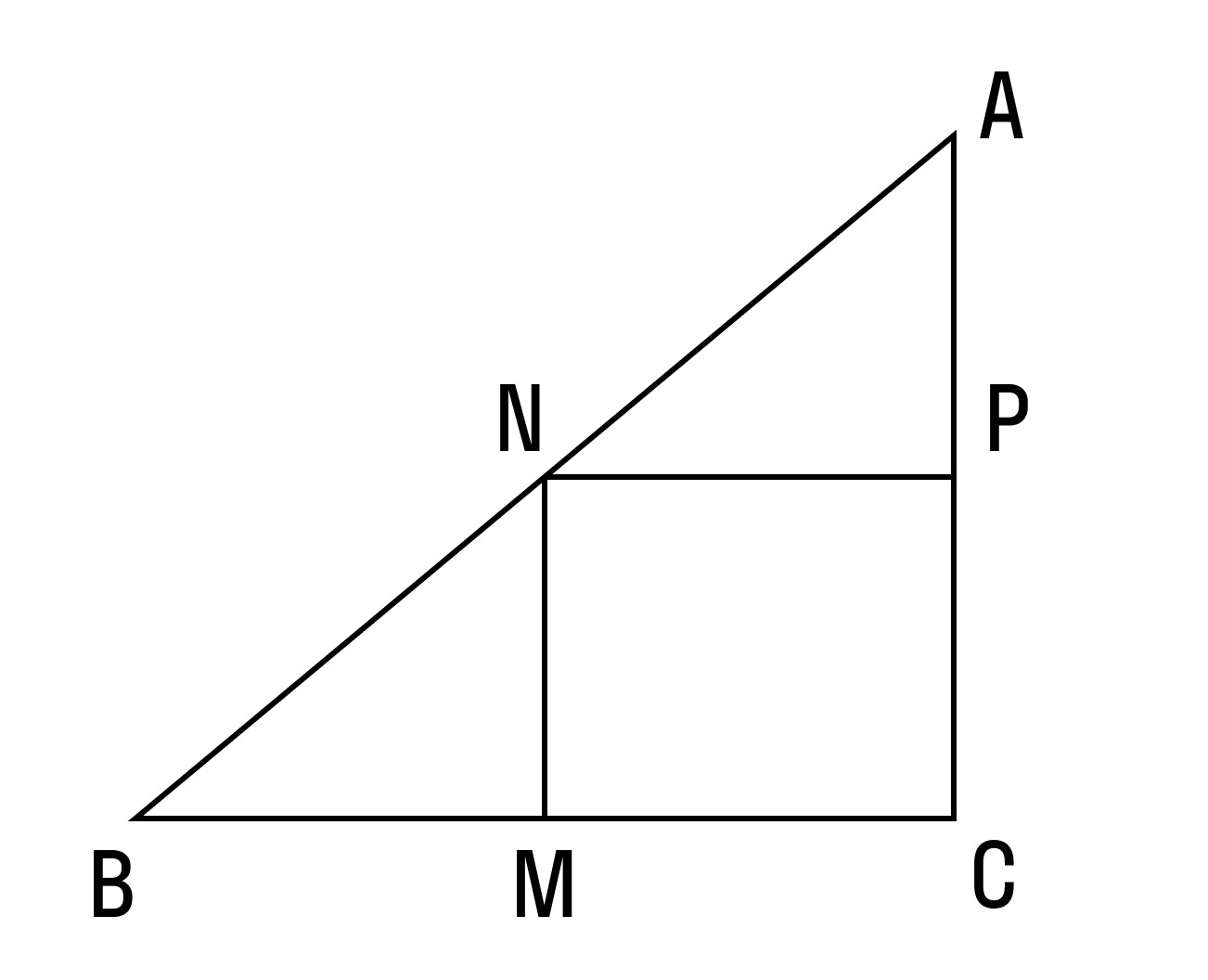
Докажем теорему:
По условию нам дано, что MA = MB, NA = NC
Рассмотрим два образовавшихся треугольника ΔAMN и ΔABC.
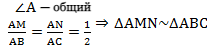
△ABC, то 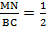
Параллельность средней линии и соответствующего ей основания доказана.
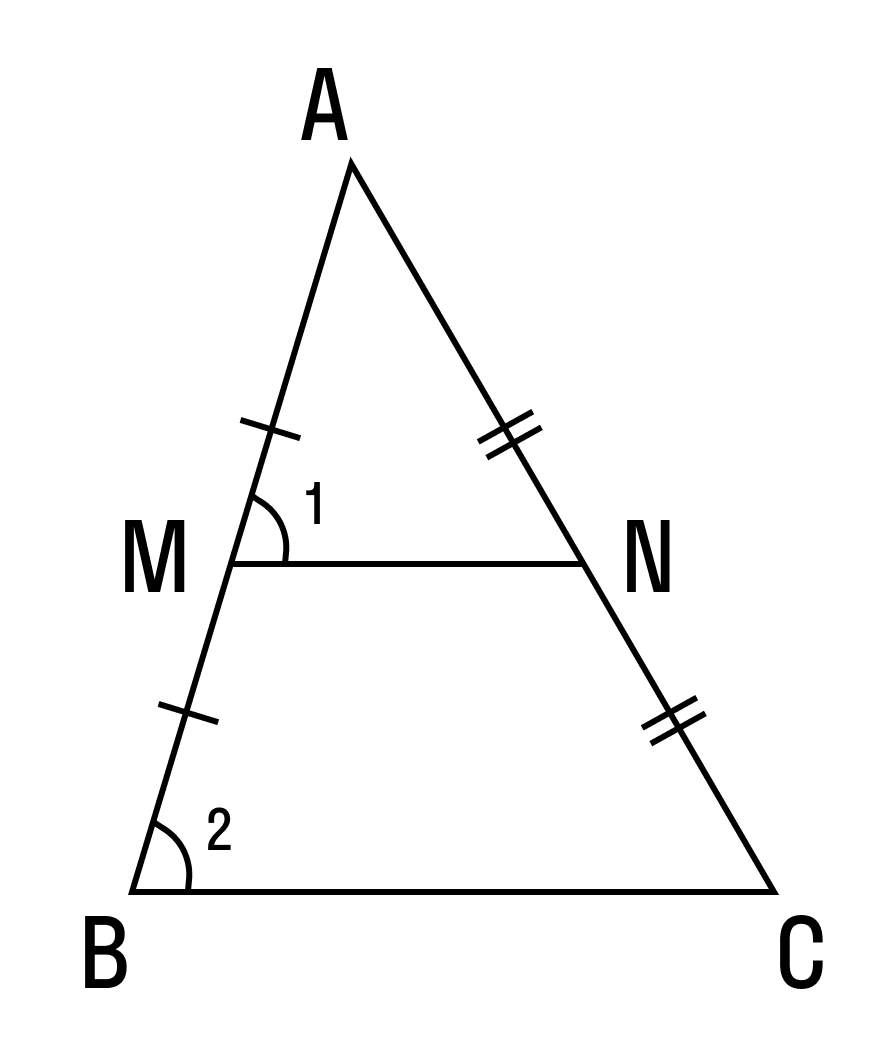
Пример 1. В треугольнике ΔABC AB = 8, BC = 7, CA = 5, точки M, K, N — середины сторон AB, BC, CA соответственно. Найти периметр ΔMNK.
Соединим середины сторон треугольника ΔABC и получим его средние линии, которые образуют треугольник ΔMNK. Найдем их длины по теореме о средней линии:
Ответ: периметр треугольника ΔMNK равен 10.
Пример 2. В прямоугольном треугольнике АВС есть две средние линии: MN и NP, равные 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.
Площадь треугольника равна половине произведения основания на высоту. Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:
Так как MN — средняя линия, то по теореме о средней линии она равна половине катета AC:
Значит, AC = 2MN = 2 × 3 = 6.
Так как NP — средняя линия, то по теореме о средней линии она равна половине катета BC:
Значит, BC = 2NP = 2 × 4 = 8.
Тогда найдем площадь большого треугольника, используя формулу, указанную выше:
S = ½ × 6 × 8 = ½ × 48 = 24.
Ответ: площадь большого прямоугольного треугольника равна 24.
Прямая проходит через середины двух сторон треугольника докажите что высоты
§ 48. СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА
Теорема. Отрезок,соединяющий середины двух сторон треугольника, параллелен третьей стороне треугольника и равен ее половине.
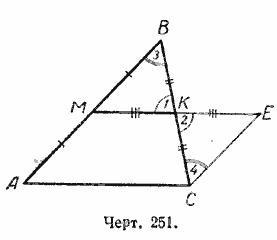
Доказательство. Продолжим МК на отрезок КЕ = МК и точку С соединим с точкой Е (черт. 251).
Рассмотрим треугольники МВК и КЕС.
СК = КВ — по условию,
КЕ = МК — по построению,
/ 1 = / 2, как вертикальные
Следовательно /\ МВК = /\ КЕС
Из равенства этих треугольников следует:
1) ЕС = МВ и, значит, ЕС = АМ;
2) / 4 = / 3, но это углы внутренние накрест лежащие при прямых ЕС и МВ и секущей ВС, следовательно, ЕС || МВ и, значит, ЕС || АМ.
Рассмотрим теперь четырёхугольник АМЕС. В нем ЕС = АМ и ЕС || АМ, поэтому
АМЕС — параллелограмм (§ 43, п. 3).
1) МЕ || АС и, значит, МК ||АС,
2) МЕ = AС и, значит, МК = AC /2
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.
1. Доказать, что прямая, проходящая через середину какой-либо стороны треугольника параллельно другой его стороне, делит третью сторону треугольника пополам.
2. Доказать, что отрезки, соединяющие последовательно середины сторон любого четырёхугольника, образуют параллелограмм.
Указание. Провести в четырёхугольнике диагонали.
3. Диагонали четырёхугольника равны 38 мм и 36 мм. Вычислить периметр параллелограмма, образованного отрезками, соединяющими середины сторон этого четырёхугольника.