Прямая призма что это

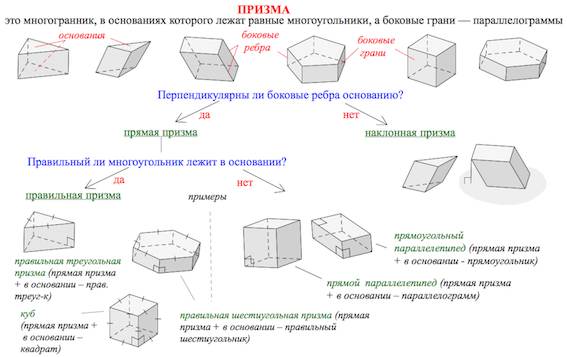
Призма. Виды призмы

Если вы уже знакомы с призмой, и хотите для себя просто что-то уточнить, то вам вполне может хватить таблицы, что дана в конце статьи.

Мы же поведем подробный разговор.

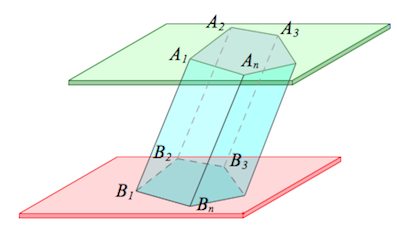
Призмой (n-угольной призмой) называется многогранник, составленный из двух равных многоугольников и , лежащих в параллельных плоскостях, и параллелограммов .

Боковые грани – все грани, кроме оснований ( являются параллелограммами ).

Боковые ребра – общие стороны боковых граней ( параллельны между собой и равны ).

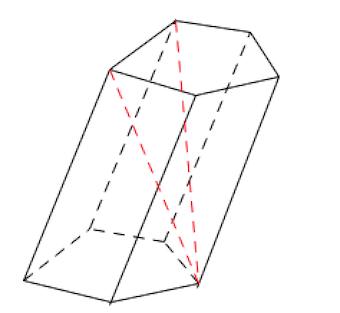
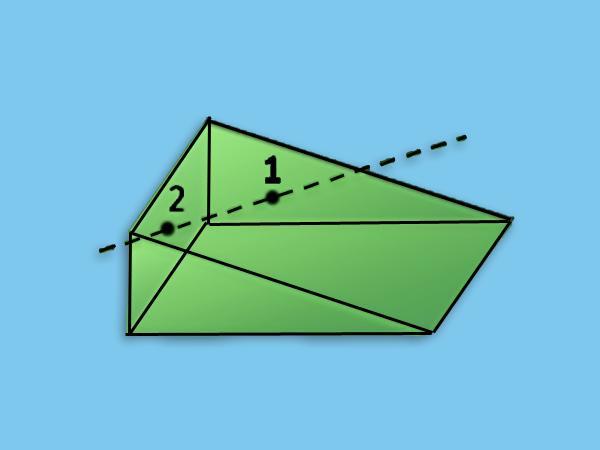
Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.

Высота призмы – перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания.

Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания.

Диагональное сечение –пересечение призмы и диагональной плоскости.

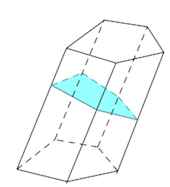
Перпендикулярное сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.

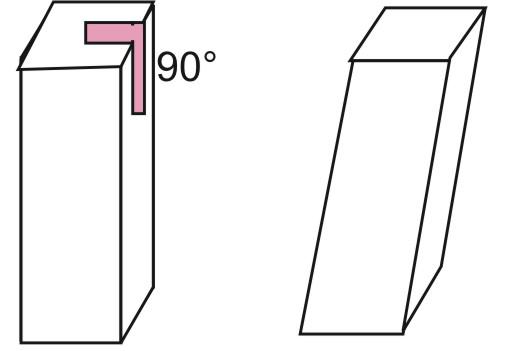
Различают призмы прямые (боковые ребра перпендикулярны плоскости основания) и наклонные (не прямые).

Среди прямых призм выделяют правильные.

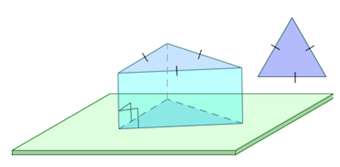
Правильная призма – это прямая призма, основанием которой является правильный многоугольник (равносторонний треугольник, квадрат, правильный шестиугольник и т.п.).

Параллелепипед – это призма, основаниями которой являются параллелограммы.

Среди параллелепипедов выделяют наклонные, прямые и прямоугольные параллелепипеды.

Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани — прямоугольники.

Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники (или прямой параллелепипед с прямоугольником в основании).

Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.

Частный случай прямоугольного параллелепипеда – куб.

Куб – прямоугольный параллелепипед, все грани которого – квадраты.

Далее – обещанная таблица, в которой собраны все основные виды призмы, с которыми приходится встречаться на ЕГЭ по математике.

Смотрите также «Объем призмы. Площадь поверхности призмы».

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Источник

Призма и ее виды

Рассматриваемый класс фигур представлен призмами нескольких видов. Перечислим их кратко:

Каждая фигура относится к одному из перечисленных трех видов классификации. Во время решения геометрических задач проще всего выполнять расчеты для правильных и прямых призм. Последние подробнее рассмотрим в следующих пунктах статьи.

Выше было сказано, что с прямыми фигурами удобно работать при решении задач. Это связано с тем, что высота совпадает с длиной бокового ребра. Последний факт облегчает процесс вычисления объема фигуры и площади ее боковой поверхности.

Объем прямой призмы

То есть произведение высоты на площадь основания даст искомое значение V. Поскольку у прямой призмы основания равны, то для определения площади So можно брать любое из них.

Преимущество использования приведенной выше формулы именно для прямой призмы в сравнении с другими ее видами заключается в том, что высоту фигуры найти очень просто, так как она совпадает с длиной бокового ребра.

Площадь боковой поверхности

Предположим, что в основании призмы лежит произвольный n-угольник, стороны которого равны ai. Индекс i пробегает значения от 1 до n. Площадь одного прямоугольника вычисляется так:

Площадь поверхности боковой Sb нетрудно вычислить, если сложить все площади Si прямоугольников. В таком случае получаем конечную формулу для Sb прямой призмы:

Таким образом, чтобы определить площадь боковой поверхности для прямой призмы, необходимо умножить ее высоту на периметр одного основания.

Задача с треугольной призмой

Для начала вычислим объем прямой призмы. Треугольник (прямоугольный), находящийся в ее основаниях, имеет площадь:

So = a1*a2/2 = 12*8/2 = 48 см2.

Как можно догадаться, a1 и a2 в этом равенстве являются катетами. Зная площадь основания и высоту (см. условие задачи), можно воспользоваться формулой для V:

V = So*h = 48*15 = 720 см3.

Полная площадь фигуры образована двумя частями: площадями оснований и боковой поверхностью. Площади двух оснований равны:

S2o = 2*So = 48*2 = 96 см2.

Для вычисления площади боковой поверхности необходимо знать периметр прямоугольного треугольника. Вычислим по теореме Пифагора его гипотенузу a3, имеем:

a3 = √(a12 + a22) = √(122 + 82) = 14,42 см.

Тогда периметр треугольника основания прямой призмы составит:

P = a1 + a2 + a3 = 12 + 8 + 14,42 = 34,42 см.

Применяя формулу для Sb, которая была записана в предыдущем пункте, получаем:

Sb = h*P = 15*34,42 = 516,3 см.

Сложив площади S2o и Sb, мы получим полную площадь поверхности изучаемой геометрической фигуры:

S = S2o + Sb = 96 + 516,3 = 612,3 см2.

Треугольная призма, которую изготавливают из специальных видов стекла, применяется в оптике при изучении спектров излучающих свет объектов. Такие призмы способны разлагать свет на составляющие частоты благодаря явлению дисперсии.

Источник

Что такое призма: определение, элементы, виды, варианты сечения

В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения призмы. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Определение призмы

Призма – это геометрическая фигура в пространстве; многогранник с двумя параллельными и равными гранями (многоугольниками), а другие грани при этом являются параллелограммами.

На рисунке ниже представлен один из самых распространенных видов призмы – четырехугольная прямая (или параллелепипед). Другие разновидности фигуры рассмотрены в последнем разделе данной публикации.

Элементы призмы

Развёртка призмы – разложение всех граней фигуры в одной плоскости (чаще всего, одного из оснований). В качестве примера – для прямоугольной прямой призмы:

Примечание: свойства призмы представлены в отдельной публикации.

Варианты сечения призмы

Примечание: другие варианты сечения не так распространены, поэтому отдельно на них останавливаться не будем.

Виды призм

Рассмотрим разновидности фигуры с треугольным основанием.

Источник

Призма. Прямая призма. Правильная призма. Объем призмы

Факт 1. Про произвольную призму \(A_1. A_nB_1. B_n\)
\(\bullet\) Многоугольники \(A_1. A_n, \ B_1. B_n\) – основания;
отрезки \(A_1B_1, \ A_2B_2\) и т.д. – боковые ребра;
четырехугольники \(A_1B_1B_2A_2\) и т.д. – боковые грани, представляющие собой параллелограммы.
\(\bullet\) Высота призмы – расстояние между ее основаниями, или, что то же самое, – перпендикуляр, опущенный из вершины одного основания к плоскости другого основания.
\(\bullet\) \(<\color<<\small<Объем \ призмы>>>>\) \[<\Large<\color>\cdot h>>>\] где \(S_<\text<осн>>\) – площадь основания, \(h\) – высота призмы.
\(\bullet\) Площадь боковой поверхности – сумма площадей ее боковых граней.
\(\bullet\) Площадь полной поверхности – сумма площади боковой поверхности и площадей оснований.

Факт 2. Про прямую призму
\(\bullet\) Призма называется прямой, если ее боковые ребра перпендикулярны основаниям.
\(\bullet\) Тогда:
1) боковые грани представляют собой прямоугольники;
2) боковое ребро является высотой призмы.

Факт 3. Про правильную призму
\(\bullet\) Призма называется правильной, если она прямая и ее основания – правильные многоугольники.
\(\bullet\) Тогда:
все боковые грани представляют собой равные прямоугольники.

Источник

Объем призмы и другие ее характеристики

Перед вами иллюстрированный гид о призме.

В картинках. С пояснениями к формулам. С примерами.

Определение, виды призм, высота, площадь, объем призмы — все, все, все!

Читайте и делитесь впечатлениями в комментариях!

Призма — коротко о главном

Определение призмы:

Призма – это многогранник, две грани которого (основания) – равные многоугольники, лежащие в параллельных плоскостях, а боковые грани – параллелограммы.

Высота призмы – перпендикуляр, опущенный из одной из вершин призмы на плоскость противоположного основания.

Виды призм:

Параллелепипед — это призма, основанием которой является параллелограмм.

Прямая призма – это призма, у которой боковые ребра перпендикулярны плоскости основания. Другие призмы называются наклонными.

Правильная призма – это прямая призма, основанием которой является правильный многоугольник. Боковые грани правильной призмы – равные прямоугольники.

Объем призмы

Главная формула объема призмы:
\( \displaystyle V=S<<\ >_<основания>>\cdot \text\),
где \( <<\text>_<основания>>\) – площадь основания,
\( H\) – высота.

Необычная формула объема призмы:
\( \text=<<\text>_<\bot >>\cdot l\),
где \( <<\text>_<\bot >>\) – площадь сечения, перпендикулярного боковому ребру,
\( l\) – длина бокового ребра.

Площадь призмы

А теперь чуть подробнее…

Заходите и готовьтесь к ЕГЭ.

Что такое призма

Давай ответим сперва картинками:

Смотри: у призмы сверху и снизу два одинаковых многоугольника – они называются основаниями.

Остальные грани называются боковыми.

Плоскости оснований параллельный. Боковые грани – параллелограммы.

Смотри: бывают рёбра основания и боковые рёбра.

Все боковые рёбра призмы равны и параллельны.

Думаю, теперь мы можем дать более строгое определение призмы.

Определение призмы

Призма — многогранник, две грани которого (основания) — равные многоугольники, лежащие в параллельных плоскостях, а боковые грани — параллелограммы.

Виды призм

Призма, основанием которой является параллелограмм, называется параллелепипедом.

Прямая призма – это призма, у которой боковые ребра перпендикулярны плоскости основания.

Другие призмы называются наклонными.

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Высота призмы

Высота призмы – перпендикуляр, опущенный из одной из вершин призмы на плоскость противоположного основания.

И ясно, что та же самая высота получится, если опустить перпендикуляр из любой точки на верхней плоскости.

Объем призмы

Главная формула объема призмы

Необычная формула объема призмы

\( \text=<<\text>_<\bot >>\cdot l\),
где \( <<\text>_<\bot >>\) — площадь сечения, перпендикулярного боковому ребру,
\( l\) — длина бокового ребра.

Площадь призмы

Прямая призма

Если боковые рёбра призмы перпендикулярны основанию, то призма называется прямой.

Свойства прямой призмы:

Правильная призма

Если боковые рёбра призмы перпендикулярны основанию, а в основании лежит правильный многоугольник, то призма называется правильной.

То есть правильная призма – это прямая призма, у которой в основании правильный многоугольник.

Тебе, скорее всего, может встретиться:

Правильная треугольная призма – в основании правильный треугольник, боковые грани – прямоугольники.

Правильная четырёхугольная призма – это ещё и разновидность прямоугольного параллелепипеда – в основании квадрат, боковые грани – прямоугольники.

Правильная шестиугольная призма – в основании правильный шестиугольник, боковые грани – прямоугольники.

Главная формула объема призмы

Эта формула верна для любой призмы, но если призма прямая, то \( H\) «превращается» в боковое ребро. И тогда

\( \displaystyle V=S<<\ >_<основания>>\cdot боковое\ ребро\)

Необычная формула объёма призмы

Представь себе, есть ещё одна, «перевёрнутая» формула для объёма призмы:

\( <<\text>_<\bot >>\) – площадь сечения, перпендикулярного боковому ребру,

\( l\) – длина бокового ребра

Используется ли эта формула в задачах? Честно говоря, довольно редко, так что можешь ограничиться знанием основной формулы объёма.

Давай теперь для упражнения посчитаем объём самых популярных призм.

Объем правильной треугольной призмы

Пусть дано, что сторона основания равна \( a\), а боковое ребро равно \( b\).

Вспомним, как находить площадь правильного треугольника:

Подставляем в формулу объёма:

Объем правильной четырёхугольной призмы

Опять дано: сторона основания равна \( a\), боковое ребро равно \( b\).

Ну, площадь квадрата долго искать не надо:

Объем правильной шестиугольной призмы

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Площадь поверхности призмы

Площадь боковой поверхности призмы – сумма площадей всех боковых граней.

Есть ли общая формула?

Нет, в общем случае нет. Просто нужно искать площади боковых граней и суммировать их.

Площадь полной поверхности призмы – сумма площадей всех граней.

Формулу можно написать для прямой призмы:

\( \displaystyle <<\text>_<боков.>>=\text\cdot \text

\), где \( \displaystyle P\) – периметр основания.

Но всё-таки гораздо проще в каждом конкретном случае сложить все площади, чем запоминать дополнительные формулы.

Для примера посчитаем полную поверхность правильной шестиугольной призмы

Пусть сторона основания равна \( \displaystyle a\), а боковое ребро равно \( \displaystyle b\).

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Наши курсы по подготовке к ЕГЭ по математике, информатике и физике

Курсы для тех, кому нужно получить 90+ и поступить в топовый ВУЗ страны.

А теперь мы хотим узнать твое мнение!

Многие ученики путают прямую и правильную призму. А ты теперь никогда не запутаешься!

Была ли эта статья полезной? Ты все понял?

Если у тебя остались вопросы, пиши внизу в комментариях! Разберёмся!

Или если появились предложения. Или если просто хочешь поделиться своими мыслями. Мы будем очень рады.

Добавить комментарий Отменить ответ

5 комментариев

Тут всё понятно,впервые начинаю понимать стереометрию

Супер Aper! Рады помочь!

Когда читаю теорию этого учебника, такое ощущение, что я разговариваю с другом. Настолько все просто и приятно. Сказать, что я влюбилась в этот материал, ничего не сказать. Спасибо вам!

Бася, вы нас растрогали таким комментарием. Спасибо большое! Удачи на экзамене!

Некоторые комментарии прошлых лет об этой статье:

Илья
26 ноября 2017
Огромное вам спасибо за созданный сайт, он очень удобен и информативен. Мне сложно представить какое количество времени было потрачено на «переработку» материала в понятном и доступном виде.Теперь есть источник чистых знаний, без лишней «воды», который не только помогает узнать новое, но и систематизировать информацию в голове. Жаль, что я не нашел сайт раньше. Вы лучшие!

Дмитрий
21 февраля 2018
Сайт отличный!Все подробно описано. Никогда не понимал эту тему, но благодаря создателям этого сайта я наконец понял эту тему. Спасибо вам за ваши труды. Очень вам благодарен.

Regina
29 марта 2018
Аааааааа,это просто лучшее. Никогда не разбиралась в геометрии…Готовясь к зачету искала все сайты на эту тему. Нашла вас. Ввы все объяснили просто и доступно. Спасибо большое!

Настя
21 мая 2018
Красивый сайт, ничего глаза не режет, смотреть и читать приятно.

Женя
27 февраля 2019
можете указать свои инициалы? мне это для проекта надо)

Анна
29 апреля 2019
Преподнесено очень понятным языком, с наглядными картинками, спасибо) Хотелось бы хоть пример одной задачи и решение чтобы было открыто бесплатно, чтобы понять на сколько хорошо поясняете, но я думаю все ок.

Жанна
27 апреля 2020
Спасибо! Я — учитель и мне очень понравилось!

Николай
04 июня 2020
Все очень доступно и понятно. Только вот не написано в статье про диагональ призмы. А так все просто супер, подготовился к сессии по данному материалу 🙂

Алексей Шевчук
05 июня 2020
Николай, спасибо. Диагонали в разных призмах разные, а в треугольной её и вовсе нет, поэтому длина диагонали — частный случай, а не какая-то полезная формула. Стоит рассмотрения разве что диагональ прямоугольного параллелепипеда — она вычисляется по теореме Пифагора и равна корню из суммы квадратов рёбер.

Источник