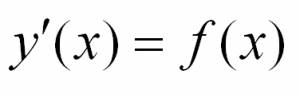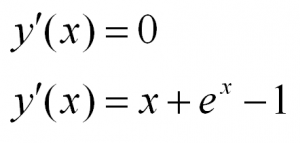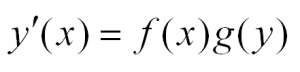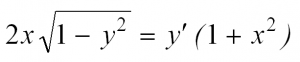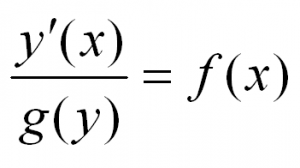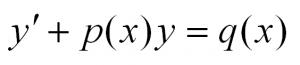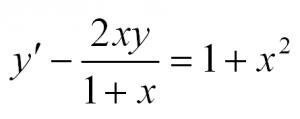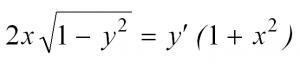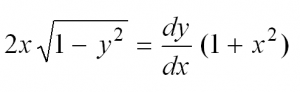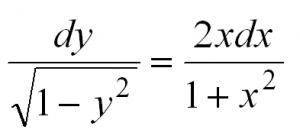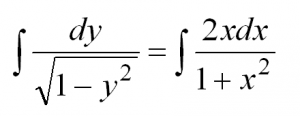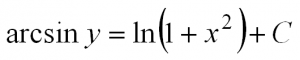Проверьте что функция удовлетворяет дифференциальному уравнению
Дифференциальные уравнения для «чайников». Примеры решения
Часто одно лишь упоминание дифференциальных уравнений вызывает у студентов неприятное чувство. Почему так происходит? Чаще всего потому, что при изучении основ материала возникает пробел в знаниях, из-за которого дальнейшее изучение диффуров становиться просто пыткой. Ничего не понятно, что делать, как решать, с чего начать?
Однако мы постараемся вам показать, что диффуры – это не так сложно, как кажется.
Основные понятия теории дифференциальных уравнений
Со школы нам известны простейшие уравнения, в которых нужно найти неизвестную x. По сути дифференциальные уравнения лишь чуточку отличаются от них – вместо переменной х в них нужно найти функцию y(х), которая обратит уравнение в тождество.
Дифференциальные уравнения имеют огромное прикладное значение. Это не абстрактная математика, которая не имеет отношения к окружающему нас миру. С помощью дифференциальных уравнений описываются многие реальные природные процессы. Например, колебания струны, движение гармонического осциллятора, посредством дифференциальных уравнений в задачах механики находят скорость и ускорение тела. Также ДУ находят широкое применение в биологии, химии, экономике и многих других науках.
Дифференциальное уравнение (ДУ) – это уравнение, содержащее производные функции y(х), саму функцию, независимые переменные и иные параметры в различных комбинациях.
Существует множество видов дифференциальных уравнений: обыкновенные дифференциальные уравнения, линейные и нелинейные, однородные и неоднородные, дифференциальные уравнения первого и высших порядков, дифуры в частных производных и так далее.
Решением дифференциального уравнения является функция, которая обращает его в тождество. Существуют общие и частные решения ДУ.
Общим решением ДУ является общее множество решений, обращающих уравнение в тождество. Частным решением дифференциального уравнения называется решение, удовлетворяющее дополнительным условиям, заданным изначально.
Порядок дифференциального уравнения определяется наивысшим порядком производных, входящих в него.
Обыкновенные дифференциальные уравнения
Обыкновенные дифференциальные уравнения – это уравнения, содержащие одну независимую переменную.
Рассмотрим простейшее обыкновенное дифференциальное уравнение первого порядка. Оно имеет вид:
Решить такое уравнение можно, просто проинтегрировав его правую часть.
Примеры таких уравнений:
Уравнения с разделяющимися переменными
В общем виде этот тип уравнений выглядит так:
Решая такое уравнение, нужно разделить переменные, приведя его к виду:
После этого останется проинтегрировать обе части и получить решение.
Линейные дифференциальные уравнения первого порядка
Такие уравнения имеют вид:
Здесь p(x) и q(x) – некоторые функции независимой переменной, а y=y(x) – искомая функция. Приведем пример такого уравнения:
Решая такое уравнение, чаще всего используют метод вариации произвольной постоянной либо представляют искомую функцию в виде произведения двух других функций y(x)=u(x)v(x).
Для решения таких уравнений необходима определенная подготовка и взять их “с наскока” будет довольно сложно.
Пример решения ДУ с разделяющимися переменными
Вот мы и рассмотрели простейшие типы ДУ. Теперь разберем решение одного из них. Пусть это будет уравнение с разделяющимися переменными.
Сначала перепишем производную в более привычном виде:
Затем разделим переменные, то есть в одной части уравнения соберем все «игреки», а в другой – «иксы»:
Теперь осталось проинтегрировать обе части:
Интегрируем и получаем общее решение данного уравнения:
Конечно, решение дифференциальных уравнений – своего рода искусство. Нужно уметь понимать, к какому типу относится уравнение, а также научиться видеть, какие преобразования нужно с ним совершить, чтобы привести к тому или иному виду, не говоря уже просто об умении дифференцировать и интегрировать. И чтобы преуспеть в решении ДУ, нужна практика (как и во всем). А если у Вас в данный момент нет времени разбираться с тем, как решаются дифференциальные уравнения или задача Коши встала как кость в горле или вы не знаете, как правильно оформить презентацию, обратитесь к нашим авторам. В сжатые сроки мы предоставим Вам готовое и подробное решение, разобраться в подробностях которого Вы сможете в любое удобное для Вас время. А пока предлагаем посмотреть видео на тему «Как решать дифференциальные уравнения»:
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Примеры решения дифференциальных уравнений с ответами
Простое объяснение принципов решения дифференциальных уравнений и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Алгоритм решения дифференциальных уравнений
Дифференциальное уравнение – это уравнение, содержащее саму функцию (y=y(x)), производные функции или дифференциалы (y′, y″) и независимые переменные (наиболее распространённая – х). Обыкновенным дифференциальным уравнением называют уравнение, в котором содержится неизвестная функция под знаком производной или под знаком дифференциала.
Чтобы решить ДУ, необходимо найти множество всех функций, которые удовлетворяют данному уравнению. Это множество в большинстве случаев выглядит следующим образом:y=f(x; С), где С – произвольная постоянная.
Проверить решённое ДУ можно, подставив найденную функцию в изначальное уравнение и убедившись, что уравнение обращается в тождество (равенство).
Примеры решения дифференциальных уравнений
Задание
Решить дифференциальное уравнение xy’=y.
Решение
В первую очередь, необходимо переписать уравнение в другой вид. Пользуясь
переписываем дифференциальное уравнение, получаем
Дальше смотрим, насколько реально разделить переменные, то есть путем обычных манипуляций (перенос слагаемых из части в часть, вынесение за скобки и пр.) получить выражение, где «иксы» с одной стороны, а «игреки» с другой. В данном уравнении разделить переменные вполне реально, и после переноса множителей по правилу пропорции получаем
Далее интегрируем полученное уравнение:
В данном случае интегралы берём из таблицы:
После того, как взяты интегралы, дифференциальное уравнение считается решённым. Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения.
– это общий интеграл. Также для удобства и красоты, его можно переписать в другом виде: y=Cx, где С=Const
Ответ
Задание
Найти частное решение дифференциального уравнения
Решение
Действуем по тому же алгоритму, что и в предыдущем решении.
Переписываем производную в нужном виде, разделяем переменные и интегрируем полученное уравнение:
Получили общий интеграл.Далее, воспользуемся свойством степеней, выразим у в «общем» виде и перепишем функцию:
Если – это константа, то
0\]» title=»Rendered by QuickLaTeX.com» />
– тоже некоторая константа, заменим её буквой С:
– убираем модуль и теперь константа может принимать и положительные, и отрицательные значения.
Получаем общее решение:
Ответ
Задание
Решить дифференциальное уравнение
Решение
В первую очередь необходимо переписать производную в необходимом виде:
Второй шаг – разделение переменных и перенос со сменой знака второго слагаемого в правую часть:
После разделения переменных, интегрируем уравнение, как в примерах выше.
Чтобы решить интегралы из левой части, применим метод подведения функции под знак дифференциала:
В ответе мы получили одни логарифмы и константу, их тоже определяем под логарифм.
Далее упрощаем общий интеграл:
Приводим полученный общий интеграл к виду: F(x,y)=C:
Чтобы ответ смотрелся красивее, обе части необходимо возвести в квадрат.
Ответ
Задание
Найти частное решение дифференциального уравнения
удовлетворяющее начальному условию y(0)=ln2.
Решение
Первый шаг – нахождение общего решения. То, что в исходном уравнении уже находятся готовые дифференциалы dy и dx значительно упрощает нам решение.
Начинаем разделять переменные и интегрировать уравнение:
Мы получили общий интеграл и следующий шаг – выразить общее решение. Для этого необходимо прологарифмировать обе части. Знак модуля не ставим, т.к. обе части уравнения положительные.
Получаем общее решение:
Далее необходимо найти частное решение, которое соответствует заданному начальному условию y(0)=ln2.
В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:
Подставляем найденное значение константы C=1 в общее решение.
Ответ
Задание
Решить дифференциальное уравнение
Решение
При внимательном разборе данного уравнения видно, что можно разделить переменные, что и делаем, после интегрируем:
В данном случае константу C считается не обязательным определять под логарифм.
Ответ
Задание
Найти частное решение дифференциального уравнения
удовлетворяющее начальному условию y(1)=e. Выполнить проверку.
Решение
Как и в предыдущих примерах первым шагом будет нахождение общего решения. Для этого начинаем разделять переменные:
Общий интеграл получен, осталось упростить его. Упаковываем логарифмы и избавляемся от них:
можно выразить функцию в явном виде.
Осталось найти частное решение, удовлетворяющее начальному условию y(1)=e.
Подставляем найденное значение константы C=1 в общее решение.
Ответ
Проверка
Необходимо проверить, выполняется ли начальное условие:
Из равенства выше видно, что начальное условие y(1)=e выполнено.
Далее проводим следующую проверку: удовлетворяет ли вообще частное решение
дифференциальному уравнению. Для этого находим производную:
Подставим полученное частное решение
и найденную производную в исходное уравнение
Получено верное равенство, значит, решение найдено правильно.
Задание
Найти общий интеграл уравнения
Решение
Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:
Ответ
Задание
Найти частное решение ДУ.
Решение
Данное ДУ допускает разделение переменных. Разделяем переменные:
Найдем частное решение (частный интеграл), соответствующий заданному начальному условию
Подставляем в общее решение
Ответ
Задание
Решить дифференциальное уравнение
Решение
Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:
Левую часть интегрируем по частям:
В интеграле правой части проведем замену:
(здесь дробь раскладывается методом неопределенных коэффициентов)
Ответ
Задание
Решить дифференциальное уравнение
Решение
Данное уравнение допускает разделение переменных.
Разделяем переменные и интегрируем:
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей: