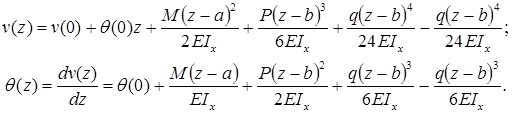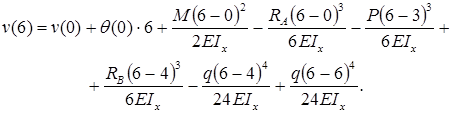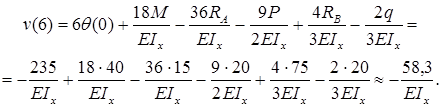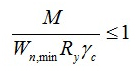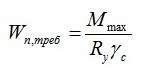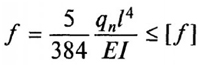Прогиб в чем измеряется

Прогиб в чем измеряется

Балкой называют конструктивный элемент, способный выдерживать большие нагрузки на изгиб. В случае малых прогибов форму балки можно описать линейным дифференциальным уравнением \(4\)-го порядка.

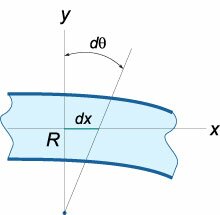
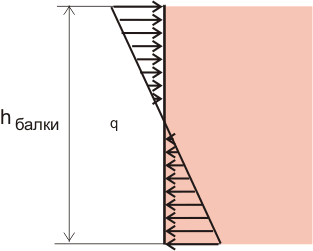
Рассмотрим вывод данного уравнения. При изгибе балки между двумя смежными сечениями, отстоящими друг от друга на расстоянии \(dx,\) образуется угол \(d\theta\) (рисунок \(1\)).

При этом деформация \(\varepsilon \) в каждой точке будет пропорциональна координате \(y,\) которую будем отсчитывать от нейтральной линии. Длина нейтральной линии считается неизменной.

Из геометрии рисунка \(1\) следует, что \[\varepsilon = \frac,\] где \(R\) − радиус кривизны бруса.

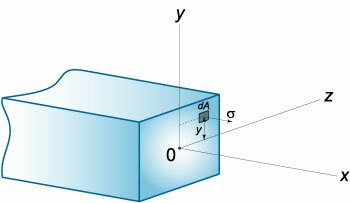
Величина нормального напряжения \(\sigma\) в сечении будет также зависеть от координаты \(y.\) Ее можно оценить по закону Гука: \[\sigma = \varepsilon E = \fracy,\] где \(E\) − модуль упругости балки.

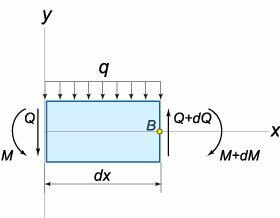
Изгибающий момент \(M\left( x \right)\) для заданного сечения балки относительно оси \(Oz\) вычисляется по формуле \[ = \int\limits_A <\sigma ydA>> = <\frac\int\limits_A <dA> > = <\fracI,> \] где \(I\) − момент инерции поперечного сечения относительно нейтральной оси \(Oz\) (рисунок \(2\)). Отсюда получаем выражение для радиуса кривизны балки: \[R = \frac<><>.\] Известно, что радиус кривизны определяется формулой \[R = \frac <<<<\left[ <1 + <<\left( \right)>^2>> \right]>^<\large\frac<3><2>\normalsize>>>><>.\] Считая прогиб балки достаточно малым, можно пренебречь первой производной \(y’.\) Тогда дифференциальное уравнение упругой линии записывается в следующем виде: \[y» = \frac<><>\;\;\text<или>\;\;\frac<<y>><>> = \frac<><>.\] Изгибающий момент \(\) можно выразить через известную внешнюю нагрузку \(,\) действующую на балку. Действительно, выделим малый элемент \(dx\) и рассмотрим условия его равновесия (рисунок \(3\)).

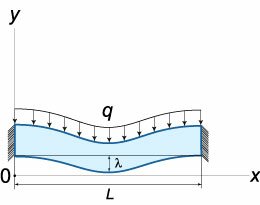
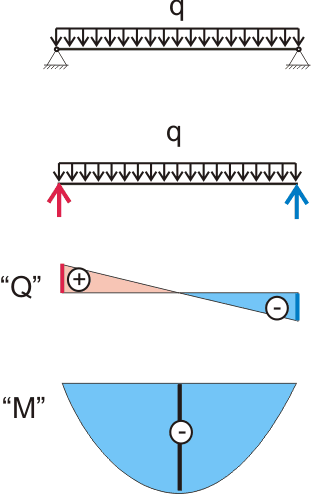
Пусть на балку длиной \(L\) действует однородно распределенная сила \(q.\) Модуль упругости \(E\) и момент инерции балки \(I\) считаем известными.

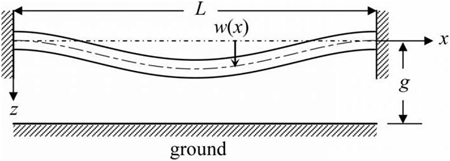
Тонкий цилиндрический вал длиной \(L\) вращается с угловой скоростью \(\omega.\) При какой скорости \(\omega\) может произойти разрушение вала? Модуль упругости материала \(E,\) масса вала \(M,\) радиус сечения \(a.\)

При вращении вала на него действует центробежная сила, которая пропорциональна отклонению \(y\) от оси вращения. При увеличении в некоторой точке деформации \(y\) центробежная сила в этой точке также будет возрастать, что приведет к дальнейшему искривлению вала. Неустойчивость такого рода возникает при определенных частотах и может привести к разрушению вала.

Исследуем эту задачу с помощью дифференциального уравнения. Базовое уравнение, описывающее деформацию вала, записывается в виде: \[EI\frac<<y>><>> = f,\] где \(f\) обозначает плотность центробежной силы.

прогиб вала в точках \(x = 0\) и \(x = L\) равен нулю;

кривизна вала в точках \(x = 0\) и \(x = L\) равна нулю.

Источник

Универсальное уравнение оси изогнутой балки, вычисление прогибов и углов поворота поперечных сечений

Определение прогибов и углов поворота поперечного сечения балки определяют с помощью универсального уравнения изогнутой оси балки (универсального уравнения упругой линии балки)

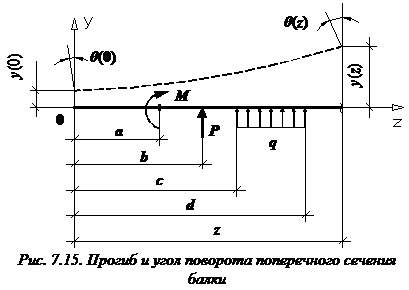
Формула (закон изменения) прогиба балки в сечении с координатой z и угол поворота сечения (рис. 7.15):

a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P, соответственно; c и d – координаты начала и конца участка, нагруженного распределенной нагрузкой.

В формулы входят только внешние усилия, которые расположены левее сечения, в котором определяются перемещения балки.

Если какая-нибудь нагрузка имеет противоположное указанному на рисунке 7.15 направление, то у соответствующих слагаемых в формулах прогибов и углов поворота сечений следует поменять знак на противоположный.

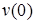
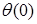
Прогиб и угол поворота балки в начале координат (начальные параметры) определяются из условий закрепления балки.

Уравнение упругой линии балки на примере

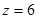
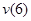
Определим прогиб балки на консоли при м, то есть . Запишем универсальное уравнение упругой линии балки :

Прогиб балки в начале координат (на левой шарнирной опоре), равен нулю: .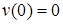

Для определения угла поворота в начале координат необходимо составить дополнительное условие: прогиб на правой опоре равен нулю.

,

.

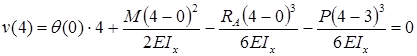
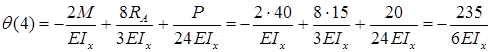
Прогиб консоли при z=6м:

Знак «минус» говорит: прогиб балки на консоли происходит вниз. Число, стоящее в числителе, измеряется в килоньютонах на метр в кубе (кН·м3).

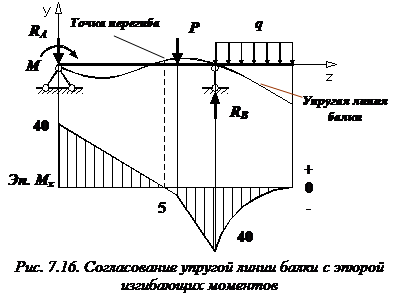
Примерный вид упругой линии балки показан на рис. 7.16.

Упругая линия балки должна быть согласована с эпюрой изгибающих моментов по дифференциальным зависимостям. Точка перегиба находится под сечением балки, в котором изгибающий момент равен нулю, что следует из закона Гука при изгибе.

Источник

Формулы для расчета прогиба балки

Балка является основным элементом несущей конструкции сооружения. При строительстве важно провести расчет прогиба балки. В реальном строительстве на данный элемент действует сила ветра, нагружение и вибрации. Однако при выполнении расчетов принято принимать во внимание только поперечную нагрузку или проведенную нагрузку, которая эквивалентна поперечной.

При расчете балка воспринимается как жесткозакрепленный стержень, который устанавливается на двух опорах. Если она устанавливается на трех и более опорах, расчет ее прогиба является более сложным, и провести его самостоятельно практически невозможно. Основное нагружение рассчитывается как сумма сил, которые действуют в направлении перпендикулярного сечения конструкции. Расчетная схема требуется для определения максимальной деформации, которая не должна быть выше предельных значений. Это позволит определить оптимальный материал необходимого размера, сечения, гибкости и других показателей.

Виды балок

Для строительства различных сооружений применяются балки из прочных и долговечных материалов. Такие конструкции могут отличаться по длине, форме и сечению. Чаще всего используются деревянные и металлические конструкции. Для расчетной схемы прогиба большое значение имеет материал элемента. Особенность расчета прогиба балки в данном случае будет зависеть от однородности и структуры ее материала.

Деревянные

Для постройки частных домов, дач и другого индивидуального строительства чаще всего используются деревянные балки. Деревянные конструкции, работающие на изгиб, могут использоваться для потолочных и напольных перекрытий.

Для расчета максимального прогиба следует учитывать:

Допустимый прогиб балки учитывает максимальный реальный прогиб, а также возможные дополнительные эксплуатационные нагрузки.

Стальные

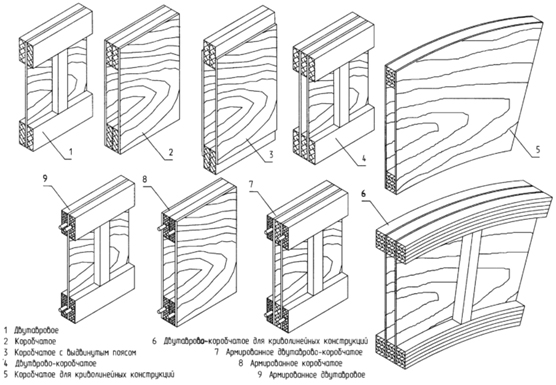
Металлические балки отличаются сложным или даже составным сечением и чаще всего изготавливаются из нескольких видов металла. При расчете таких конструкций требуется учитывать не только их жесткость, но и прочность соединений.

Металлические конструкции изготавливаются путем соединения нескольких видов металлопроката, используя при этом такие виды соединений:

Стальные балки чаще всего применяются для многоэтажных домов и других видов строительства, где требуется высокая прочность конструкции. В данном случае при использовании качественных соединений гарантируется равномерно распределенная нагрузка на балку.

Для проведения расчета балки на прогиб может помочь видео:

Прочность и жесткость балки

Чтобы обеспечить прочность, долговечность и безопасность конструкции, необходимо выполнять вычисление величины прогиба балок еще на этапе проектирования сооружения. Поэтому крайне важно знать максимальный прогиб балки, формула которого поможет составить заключение о вероятности применения определенной строительной конструкции.

Использование расчетной схемы жесткости позволяет определить максимальные изменения геометрия детали. Расчет конструкции по опытным формулам не всегда эффективен. Рекомендуется использовать дополнительные коэффициенты, позволяющие добавить необходимый запас прочности. Не оставлять дополнительный запас прочности – одна из основных ошибок строительства, которая приводит к невозможности эксплуатации здания или даже тяжелым последствиям.

Существует два основных метода расчета прочности и жесткости:

Последний метод является наиболее точным и достоверным, ведь именно он помогает определить, какую именно нагрузку сможет выдержать балка.

Расчет на жесткость

Для расчета прочности балки на изгиб применяется формула:

M – максимальный момент, который возникает в балке;

W_n,min – момент сопротивления сечения, который является табличной величиной или определяется отдельно для каждого вида профиля.

R_y является расчетным сопротивлением стали при изгибе. Зависит от вида стали.

γ_c представляет собой коэффициент условий работы, который является табличной величиной.

Чтобы составить расчетную схему, потребуются такие данные:

Если производится расчет двухопорной балки, то одна опора считается жесткой, а вторая – шарнирной.

Расчет моментов инерции и сопротивления сечения

Для выполнения расчетов жесткости потребуется значение момент инерции сечения (J) и момента сопротивления (W). Для расчета момента сопротивления сечения лучше всего воспользоваться формулой:

Важной характеристикой при определении момента инерции и сопротивления сечения является ориентация сечения в плоскости разреза. При увеличении момента инерции увеличивается и показатель жесткости.

Определение максимальной нагрузки и прогиба

Для точного определения прогиба балки, лучше всего применять данную формулу:

q является равномерно-распределенной нагрузкой;

E – модуль упругости, который является табличной величиной;

I – момент инерции сечения.

Чтобы рассчитать максимальную нагрузку, следует учитывать статические и периодические нагрузки. К примеру, если речь идет о двухэтажном сооружении, то на деревянную балку будет постоянно действовать нагрузка от ее веса, техники, людей.

Особенности расчета на прогиб

Расчет на прогиб проводится обязательно для любых перекрытий. Крайне важен точный расчет данного показателя при значительных внешних нагрузках. Сложные формулы в данном случае использовать необязательно. Если использовать соответствующие коэффициенты, то вычисления можно свести к простым схемам:

Применение этого метода вычисления прогиба позволяет не учитывать материал. Поэтому на расчеты не влияют значения его основных характеристик.

Пример подсчета прогиба

Чтобы понять процесс расчета жесткости балки и ее максимального прогиба, можно использовать простой пример проведения расчетов. Данный расчет проводится для балки с такими характеристиками:

Для вычисления максимальной допустимой нагрузки учитывается вес балки, перекрытий и опор. Рекомендуется также учесть вес мебели, приборов, отделки, людей и других тяжелых вещей, который также будут оказывать воздействие на конструкцию. Для расчета потребуются такие данные:

Чтобы упросить расчет данного примера, можно принять массу перекрытия за 60 кг/м², нагрузку на каждое перекрытие за 250 кг/м², нагрузки на перегородки 75 кг/м², а вес метра балки равным 18 кг. При расстоянии между балками в 60 см, коэффициент k будет равен 0,6.

Если подставить все эти значения в формулу, то получится:

q = ( 60 + 250 + 75 ) * 0,6 + 18 = 249 кг/м.

Для расчета изгибающего момента следует воспользоваться формулой f = (5 / 384) * [(qn * L4) / (E * J)] £ [¦].

Подставив в нее данные, получается f = (5 / 384) * [(qn * L4) / (E * J)] = (5 / 384) * [(249 * 44) / (100 000 * 10)] = 0,13020833 * [(249 * 256) / (100 000 * 10)] = 0,13020833 * (6 3744 / 10 000 000) = 0,13020833 * 0,0000063744 = 0,00083 м = 0,83 см.

Именно это и является показателем прогиба при воздействии на балку максимальной нагрузки. Данные расчеты показывают, что при действии на нее максимальной нагрузки, она прогнется на 0,83 см. Если данный показатель меньше 1, то ее использование при указанных нагрузках допускается.

Использование таких вычислений является универсальным способом вычисления жесткости конструкции и величины их прогибания. Самостоятельно вычислить данные величины достаточно легко. Достаточно знать необходимые формулы, а также высчитать величины. Некоторые данные необходимо взять в таблице. При проведении вычислений крайне важно уделять внимание единицам измерения. Если в формуле величина стоит в метрах, то ее нужно перевести в такой вид. Такие простые ошибки могут сделать расчеты бесполезными. Для вычисления жесткости и максимального прогиба балки достаточно знать основные характеристики и размеры материала. Эти данные следует подставить в несколько простых формул.

Источник

Основы сопромата, расчет прогиба балки

Часто при расчете строительных конструкций важно определить не только геометрические параметры сечения конструкции, но и величину прогиба конструкции с точностью до миллиметра. Дело в том, что величина прогиба для любой конструкции нормируется различными СНиПами и не должна превышать 1/250 для балок междуэтажных перекрытий, 1/200 для чердачных перекрытий и перемычек и так далее, список длинный. Когда расчет производится для себя (например строится частный дом и нужно сделать балки перекрытия или перемычки), то определять величину прогиба не обязательно, никто Вас ругать не будет, главное чтобы по несущей способности расчет был верный, но все же определить прогиб конструкции желательно. Ведь знание величины прогиба позволить более точно выбрать, например, вариант отделки потолка.

Расчет прогиба балки не то, чтобы такой уж сложный, но для того, чтобы каждый раз не повторять одни и те же операции при расчете и этим максимально сократить время расчета, специалисты по сопромату уже давно вывели формулы для наиболее вероятных вариантов опор балок и нагрузок, действующих на балки. Достаточно только определиться с расчетной моделью балки и формула для расчета прогиба к Вашим услугам. Но аксиомы: «если хочешь, чтобы работа была сделана хорошо, сделай это сам» пока никто не отменял. Дело в том, что в разного рода справочниках и пособиях иногда бывают опечатки или ошибки, поэтому использовать готовые формулы не всегда есть хорошо.

11. Определение угла поворота.

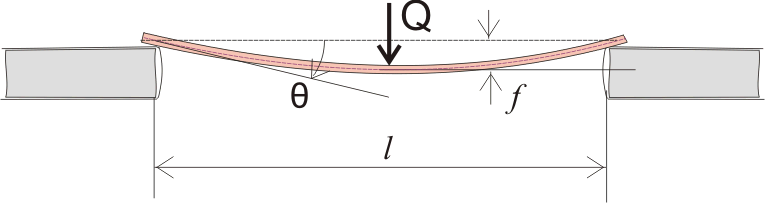
Рисунок 11.1. Перемещение центра тяжести поперечного сечения балки в центре балки и угол поворота продольной оси, проходящей через центр тяжести поперечного сечения, на одной из опор.

Фотография 1.

Но попробуем прийти к тому же результату, следуя по тернистому пути теории сопромата.

Так как балка прогнулась (в хорошем значении этого слова), получается, что и продольная ось, проходящая через центры тяжести поперечных сечений всех точек балки, и до приложения нагрузки совпадавшая с осью х, сместилась. Это смещение центра тяжести поперечного сечения по оси у называется прогибом балки f. Кроме того, очевидно, что на опоре эта самая продольная ось теперь находится под некоторым углом θ к оси х, а в точке действия сосредоточенной нагрузки угол поворота = 0, так как нагрузка у нас приложена посредине и балка прогнулась симметрично. Угол поворота принято обозначать «θ«, а прогиб «f» (во многих справочниках по сопромату прогиб обозначается как «ν«, «w» или любыми другими литерами, но нам, как практикам, удобнее использовать обозначение «f«, принятое в СНиПах).

Если мы возьмем кусок бинтовой резины и попробуем его растянуть, то обнаружим, что резина растягивается очень легко, а выражаясь по научному деформируется на значительную величину при воздействии даже небольшой нагрузки. Если мы попробуем проделать то же самое с нашей линейкой, то растянуть ее даже на десятые доли миллиметра руками вряд ли получится, даже если прилагать к линейке нагрузку в десятки раз большую, чем к бинтовой резине. Это свойство любого материала описывается модулем Юнга, который часто называется просто модулем упругости. Физический смысл модуля Юнга при максимально допустимом загружении рассчитываемой конструкции примерно следующий: модуль Юнга показывает отношение нормальных напряжений, (которые при максимально допустимом загружении равны расчетному сопротивлению материала к относительной деформации при таком загружении:

E = R/Δ (11.1.1)

а это значит, что для работы материала в области упругих деформаций значение внутренних нормальных напряжений, действующих не абстрактно, а на вполне определенную площадь сечения, с учетом относительной деформации не должно превышать значения модуля упругости:

E ≥ N/ΔS (11.1.2)

Определить величину деформации для поперечного сечения, к которому приложена равномерно распределенная нагрузка или сосредоточенная сила в центре тяжести поперечного сечения, очень просто. В таком сечении возникают нормальные сжимающие или растягивающие напряжения, равные по значению действующей силе, направленные противоположно и постоянные по всей высоте балки (согласно одной из аксиом теоретической механики):

Рисунок 507.10.1

и тогда определить относительную деформацию, если известны геометрические параметры балки (длина, ширина и высота) несложно, простейшие математические преобразования формулы (11.1.2) дают следующий результат:

Δ = Q/(S·Е) (11.2.1) или Δ = q·h/(S·Е) (11.2.2)

Так как расчетное сопротивление показывает какую максимальную нагрузку можно приложить к определенной площади, то в данном случае мы можем рассматривать действие сосредоточенной нагрузки на всю площадь сечения нашей конструкции. В некоторых случаях важно определить деформации именно в точке приложения сосредоточенной нагрузки, но сейчас мы эти случаи не рассматриваем. Чтобы определить суммарную деформацию, нужно обе части уравнения умножить на длину балки:

Δl = Q·l/(b · h·Е) (11.2.3) или Δl = q·h·l/(b · h·Е) (11.2.4)

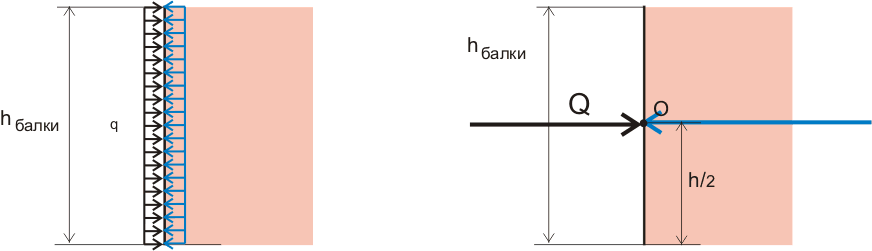
Но в рассматриваемом нами случае на поперечные сечения балки действует не сосредоточенная сила, приложенная к центру тяжести поперечного сечения, а изгибающий момент, который можно представить в виде следующей нагрузки:

Рисунок 149.8.3

При такой нагрузке максимальные внутренние напряжения и соответственно максимальные деформации будут происходить в самой верхней и в самой нижней части балки, а посредине никаких деформаций не будет. Равнодействующую для такой распределенной нагрузки и плечо действия сосредоточенной силы мы находили в предыдущей части (2), когда определяли момент сопротивления балки. Поэтому теперь без особого труда можем определить суммарную деформацию в самой верхней и в самой нижней части балки:

Δх = M·х/((h/3)·b·(h/2)·Е) (11.3.1)

Δх = M·х/(W·Е) (11.3.2)

так как W = b·h 2 /6 (10.6)

Эту же формулу мы можем получить и другим способом. Как мы знаем, момент сопротивления поперечного сечения балки должен удовлетворять следующему условию:

W ≥ М / R (10.3)

Если мы будем рассматривать эту зависимость как уравнение и заменим в этом уравнении значение R на ΔЕ, получим следующее уравнение:

W = М / ΔЕ (11.4.1)

М = WΔЕ (11.4.2) a Δ = M/(W·Е) (11.4.5) и соответственно Δх = M·х/(W·Е) (11.3.2)

В результате деформации, которую мы только что определили, наша балка могла была бы выглядеть так:

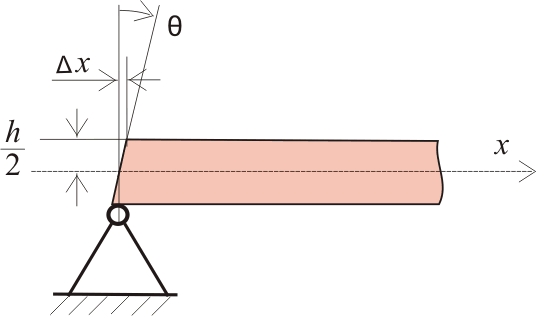
Рисунок 11.2. Предполагаемая (для наглядности) деформация балки

то есть в результате деформаций самая верхняя и самая нижняя точки поперечного сечения сместятся на величину Δх. А это значит, что зная величину деформации и высоту балки, мы можем определить угол поворота θ поперечного сечения на опоре балки. Из школьного курса геометрии мы знаем, что отношение катетов прямоугольного треугольника (в нашем случае катеты Δх и h/2) равно тангенсу угла θ:

tgφ = Δх/(h/2) (11.5.1)

tgφ = 2 M·х/(h·W·Е) (11.5.3)

W = I/(h/2) (10.7) или I = W·h/2 (10.7.2)

то мы можем заменить момент сопротивления на момент инерции:

tgφ = M·х/(I·Е) (11.5.4)

Рассчитываемые элементы далеко не всегда имеют прямоугольное сечение, как наша рассматриваемая линейка. В качестве балок и перемычек могут использоваться различные горячекатаные профили, тесанные и не тесанные бревна и вообще все, что угодно. Тем не менее понимание принципов расчета момента инерции позволяет определить момент инерции для поперечного сечения любой, даже очень сложной геометрической формы. В абсолютном большинстве случаев вычислять самому момент инерции нет необходимости, для металлических профилей сложного сечения (уголки, швеллера, двутавры и др.) момент инерции, как впрочем и момент сопротивления определяется по сортаменту. Для элементов круглого овального, треугольного сечения и некоторых других видов сечения определить момент инерции можно по соответствующей таблице.

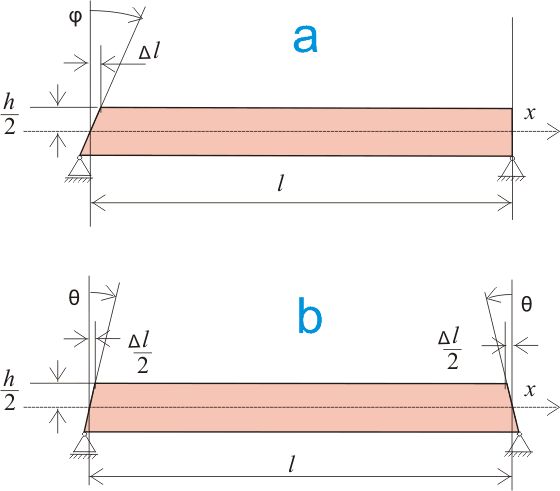
Если рассматривать суммарную деформацию всей балки, т.е. по всей длине l, то очевидно, что суммарная деформация при наших нагрузках не может быть только с одной стороны балки, как показано на рисунке 11.3.а:

Рисунок 11.3.

Так как к нашей балке нагрузка приложена посредине, в результате чего реакции на опорах, возникающие в результате действия нагрузки равны между собой и каждая равна половине приложенной нагрузки, то скорее при этих условиях суммарная деформация будет выглядеть так, как показано на рисунке 11.3.b и тогда в нашем конкретном случае угол наклона поперечного сечения на каждой из опор будет:

tgθ = M·х/(2IЕ) (11.5.5)

Рисунок 149.7.1 Рисунок 149.7.2

Примечание: как и с эпюрой моментов, тут есть особенность. Когда эпюра моментов и эпюра прогиба находятся ниже оси балки, то и момент и прогиб считаются положительными. И наоборот, когда эпюра моментов и эпюра прогиба находятся выше оси балки, то и момент и прогиб считаются отрицательными. Для инженеров-строителей это настолько привычно, что они даже не представляют, что может быть по-другому.

Характерная особенность графоаналитического метода состоит в том, что количество вычислений можно еще сократить. Для этого нужно умножить площадь эпюры фиктивной нагрузки на расстояние от центра тяжести эпюры до начала координат, а не до рассматриваемой точки на оси. Например, для вышеприведенного случая (Ql 2 /16)l/3 = Ql 3 /48

При равномерно распределенной нагрузке эпюра моментов описывается квадратичной параболой, определить площадь такой фигуры и расстояние до центра тяжести сложнее, но для того нам и нужны знания по геометрии, чтобы можно было определить площадь любой фигуры и положение центра тяжести такой фигуры. Впрочем, можно воспользоваться и готовыми формулами.

Таким образом получается, что для балки, на которую действует сосредоточенная нагрузка в середине балки при х=l/2:

tgθ = М·(x/2)/(ЕI) = ((Ql/4)·(l/4))/(ЕI) = Ql 2 /(16EI) (11.6.1)

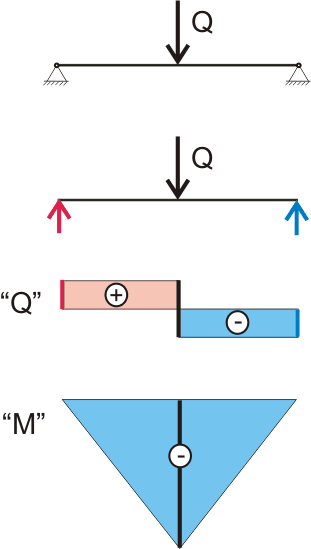
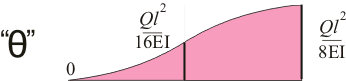
То, что мы только что делали называется интегрированием, ведь если умножить значение значение эпюры «Q» (рисунок 149.7.1) на длину действия нагрузки, мы тем самым определим площадь прямоугольника со сторонами «Q» и х, при этом площадь данного прямоугольника равняется значению эпюры «М» в точке х.

Теоретически получается, что мы можем определить значение тангенса угла поворота, интегрируя одно из уравнений моментов, составленных для нашей балки. Максимальное значение тангенса угла поворота для балки на двух шарнирных опорах, на которую действует сосредоточенная нагрузка посредине (рисунок 149.7.1), будет при х=l/2

tgθ = ∫Mdx/(EI) = ∫Axdx/(EI)= Ax 2 /(2EI) = (Q/2)·(l/2) 2 /(2ЕI) = Ql 2 /(16EI) (11.6.2)

Тот же результат мы получим и при использовании графо-аналитического метода.

Когда мы определяли угол поворота, то для наглядности предположили, что балка деформировалась так, как показано на рисунке 5.2, потом так, как показано на рисунке 11.3.b, потом мы выяснили, что если бы второй опоры не было, то балка повернулась вокруг первой опоры, но в действительности вторая опора есть и потому так балка деформироваться (при нашей нагрузке на балку) не может. Так как на опоре нет никакого вращающего момента и соответственно никаких внутренних напряжений, способных изменить геометрическую форму балки, то геометрическая форма балки на опоре остается неизменной, а внутренние напряжения, увеличивающиеся по ходу балки, деформируют балку все сильнее и это приводит к тому, что балка поворачивается вокруг шарнирных опор и этот угол поворота равен углу наклона поперечного сечения θ (так как мы рассматриваем балку-параллелепипед):

Рисунок 11.4. Реальная деформация балки.

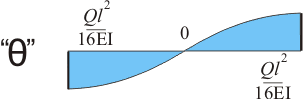
Если мы просто постоим эпюру углов поворота для балки со сосредоточенной нагрузкой посредине по уравнениям для левой и для правой части балки, то эпюра будет выглядеть так:

Рисунок 11.5.

Данная эпюра была бы правильной только для балки, изображенной на рисунке 5.3.а. Очевидно, что в нашем случае эпюра так выглядеть не может и для построения правильной эпюры нужно учесть, что поперечные сечения балки имеют наклон на обоих опорах, причем наклон этот одинаковый по значению, но разный по направлению а наклон поперечного сечения балки посредине =0. Если мы опустим эпюру на Ql 2 /16EI, которое мы получаем при интегрировании уравнения моментов для левой части балки и которое показывает угол наклона поперечного сечения именно на опоре, то получим эпюру следующего вида:

Рисунок 11.6.

Данная эпюра абсолютно точно показывает, изменение угла поворота поперечных сечений, вдоль всей балки, а значение тангенса угла поворота на левой опоре балки не что иное, как некая постоянная С₁, которую мы получаем, если интегрирование выполнять корректно. И тогда уравнение угла поворота для балки при данной нагрузке на участке 0 2 /(2EI) (11.6.5)

Ну и теперь самое главное, все эти разборки с углом поворота поперечного сечения нужны нам были для того, чтобы определить прогиб балки.

12. Определение прогиба.

Как мы видим из рисунка 11.4, треугольник с катетами h/2 и Δх является подобным треугольнику с катетом Х и вторым катетом, равным f+у, а это значит, что теперь мы можем определить значение прогиба:

tgθ = (f + y)/Х (12.1)

f + y = tgθ·X (12.2.1) или f + y = М·x·Х/(2ЕI) (12.2)

f = М·x 2 /(3ЕI) (12.3.1)

Но мы не будем ничего предполагать, а воспользуемся интегрированием. Если мы проинтегрируем уравнение моментов для левой части балки, то получим значение у (эпюра для у показана бирюзовым цветом на фотографии 1):

у =∫∫∫(Q/2)dх = (Q/2)·(l/2) 3 /6EI = Ql 3 /(96EI) (12.3.2)

или площадь фиолетовой эпюры для левой части балки(рисунок 5.5), но нам нужна площадь голубой эпюры на левом участке балки (рисунок 5.6), которая в 2 раза больше площади фиолетовой эпюры. Таким образом:

f =2∫∫∫(Q/2)dх =2 (Q/2)·(l/2) 3 /6EI = Ql 3 /(48EI) (12.3.3)

Мы можем найти значение прогиба и другим способом. Из рисунка 11.4 и формул (12.2) следует, что:

В данном случае знак «-» показывает, что центр поперечного сечения балки переместится вниз по оси у относительно оси х. А теперь вернемся к фотографии 1. Под продольной осью балки изображена эпюра у, именно это значение в точке l/2 мы и вычли, решая уравнение (12.3.3). Кроме того получается, что соотношение между f и у зависит от коэффициента предыдущего интегрирования, т.е. у = kf или f = y/k. Когда мы интегрировали уравнение сил, то получили коэффициент 1/2. Впрочем, такое же значение мы получили и тогда, когда определяли плечо действия момента. Если продолжить этот логический ряд, то получается, что при определении прогиба от распределенной нагрузки мы должны использовать коэффициент 1/3, то есть прогиб в середине балки мы можем вычислить по следующей формуле:

В данном случае знак «-» означает, что центр тяжести поперечного сечения перемещается вниз по оси у.

Примечание: Предложенный метод определения прогиба несколько отличается от общепринятых, так как я старался сделать основной упор на наглядность.

Конечно же, сосредоточенная нагрузка к балке может быть приложена и не посредине, распределенная нагрузка может быть не только равномерно распределенной и действовать не по всей длине балки, да и варианты крепления балки на опорах бывают разные. Но для того и существуют готовые формулы, чтобы ими пользоваться.

Все верно. Касательные напряжения действительно влияют на прогиб, однако для балок с соотношением l/h > 10 это влияние очень незначительно и потому допустимо для определения прогиба пользоваться изложенным в данной статье методом.

Проверяем: tgθ = Ql 2 /(16EI) = 0.302·90 2 /(16·10 5 ·0.0136) = 0.11233. Тогда согласно формулы (542.12) f = 3.37/((1 + 0.112 2 ) 3/2 ) = 3.307 см. Т.е. влияние конечно есть, но оно не превышает 2% или 0.63 мм.

13. Определение угла поворота через прогиб.

Определить значение угла поворота для шарнирно опертой балки, на которую действует только изгибающий момент M на одной из опор, например на опоре А, казалось бы, проще простого:

Как видим, угол поворота на опоре к которой приложен изгибающий момент, в два раза больше угла поворота на противоположной опоре, это очень важная закономерность, которая в дальнейшем нам очень пригодится.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

А как исходя из всех этих формул визуализировать процесс прогиба?
Я хочу написать такую программу, которая бы позволяла рассчитывать прогибы и отображала бы на рисунке, как он происходит.

А это уже вопрос не по моей части, программистом я не являюсь и потому ничего конкретного посоветовать не могу.

Спасибо за такое доступное, простое изложение материала. Благодаря Вам у меня получилось посчитать все, что нужно. Очень рада, что попала на вашу страницу. Процветайте и преуспевайте.

Спасибо! Очень наглядно! У меня такая же балка но она развернута по продольной оси на 55 градусов. Работает как пружина на сжатие. Нужно подобрать оптимальную конфигурацию балки. Сам точно не осилю. Может, кто ни нибудь готов поучаствовать за вознаграждение

Почитайте статью: «Расчет деревянной стойки на сжатие. Общие положения.» Должно помочь.

Глубокоуважаемый Доктор Лом! Не могли бы Вы рассчитать допустимый прогиб/провис железобетонного перекрытия, рассчёт которого приводили в своей статье http://doctorlom.com/item240.html?

Уважаемый Доктор Лом! Спасибо за хорошие статьи. У меня один вопрос. f измеряется в см. Я подставил размерности в формулу (6.4.6) и после сокращений получилось см^2. В чем проблема? Может l не в той степени и должно быть подобной в формуле (6.3.5)?

Спасибо за уточнение, теперь все сходится.

W = I/(h/2) (4.7) или I = W·h/2 что такое I?

В этот раз у вас одна небольшая ошибка: при переводе нагрузки на погонный сантиметр получится 0.142 кг/см, а не 0.0142 (и это похоже нагрузка только от 1 швеллера и в таком случае нужно или умножить нагрузку на 2 или не умножать момент инерции на 2). А дальше у вас большие проблемы с калькулятором, потому что даже в приведенном вами выражении получится около 0.025 см, а с учетом указанной ошибки прогиб от собственного веса составит около 0.51 см. Кстати при расчете прогиба от сосредоточенной нагрузки вы похоже также не учли, что прогибаться будут 2 швеллера и соответственно прогиб будет в 2 раза меньше.
А нашу переписку я потом возможно перемещу в отдельную статью и она никого отвлекать не будет.

Уважаемый доктор Лом как рассчитать прогиб для решетчатого прогона или он будет по той же формуле что и для сплошной балки. А как быть с шпренгельной балкой, неужели стойка может быть не меньше 1/6 пролета многовато как посчитать вручную

Прогиб f=Ql3/4Ebh3 при расчёте в см получается как описано 3,38см.
А при расчёте в метрах 0,003386436м или 3,38мм
не пойму где ошибка. значения подставлял следующие: Q=0,302кг l=0,9м E=10000000000Па
b=0,0496м h=0,0032м

Первым делом следует соблюдать размерность. Если вы использовали значение Q в килограммах, то и значение Е следует использовать в кгс/см^2 (1 МПа это приблизительно 10 кгс/см^2) или в кгс/м^2. Возможно в этом ошибка.

Для начала прочитайте статью «Прогиб пола при ходьбе», ну а после решайте, что лучше: или перебирать и усиливать перекрытие, или крепить прочно шкафы к стенам или ходить мягко и осторожно, как кошка.

Если Вы плохо освоили сопромат, зачем учить и вводить в заблуждение других? Для работы в упругой области напряжения не должны превосходить предела упругости. Напряжения, равные модулю Юнга, в сотни раз превосходят предел прочности. Читайте учебник.

Пациент, успокойтесь и просто послушайте, что я вам скажу, возможно это вам поможет.

Во-первых, подробному определению модуля Юнга посвящена отдельная статья и на эту статью есть ссылка.

И еще, вести речь о постоянном значении модуля упругости имеет смысл только в области упругих (пропорциональных) деформаций. В области пластических деформаций значение модуля упругости будет уменьшаться тем стремительнее, чем больше будет становиться относительная деформация. Так что учебник читать нужно не мне, а вам и двойка в данном случае тоже вам.

Что касается командировки в палату, так «напряжения, равные модулю Юнга» следуют из вашей же формулы (5.1.2), где присутствует знак равенства. Приведите мне хотя бы один реальный пример для строительных материалов, в котором будет знак равенства в указанной формуле! Впрочем, во фразе «напряжения, равные модулю Юнга» нет никакого внутреннего противоречия: второкурсникам, только начинающим изучать сопромат, известно, что модуль Юнга численно равен таким мысленно представляемым напряжениям при растяжении образца, при которых длина образца увеличивается вдвое (в предположении, что при таких деформациях образец не разрушается и сохраняется закон Гука). Такой вывод сразу следует из закона Гука и приведен в некоторых учебниках. Другой вопрос, что для подавляющего большинства материалов такой уровень напряжений недостижим. Модуль Юнга имеет размерность напряжений, и может сравниваться с ними. Опять о чем спор? Почему на мое замечание о модуле упругости нет ответа? Согласны с ним или тоже будете оспаривать?

То есть весь этот поток гневных обвинений из-за того, что вместо понятия «напряжения» я использовал понятие «расчетное сопротивление»? Что ж претензия принимается, тем более с академической точки зрения вы совершенно правы, но.

1. К чему мы стремимся при расчете по первой группе предельных состояний? Правильно, к тому, чтобы нормальные напряжения в рассматриваемом поперечном сечении не превышали расчетного сопротивления, а в идеале были равны.
Второй вопрос: когда мы определяем прогиб (выполняем расчет по второй группе предельных состояний)? Правильно, как правило после того, как выполнен расчет по первой группе предельных состояний, т.е. когда нормальные напряжения близки к расчетному сопротивлению или даже равны. Т.е. приведенная мной формула не просто возможна, а наиболее вероятна для множества расчетов. И если вы обратили внимание данная статьи идет, как продолжение другой статьи и начинается с пункта 5.
И последний вопрос: часто ли при расчете строительных конструкций по второй группе предельных состояний учитывается то, что расчетное сопротивление материала как правило больше предела пропорциональности и даже предела упругости, а значит и принимаемый для расчетов модуль Юнга должен быть меньше, т.е. должны учитываться пластические деформации?

3. Я внес поправку в определение физического смысла модуля упругости и если бы более внятно излагали свои мысли, то возможно сделал бы это сразу. Но если вы будете формулировать свои мысли так, как первый раз, то будете получать ответы такие же, как и в первый раз.

4. Из формулы (5.1.2) следует, что нормальные напряжения, деленные на относительную деформацию, не должны превышать значение модуля Юнга, но никак ни «напряжения, равные модулю Юнга».

Я что то не понял,почему мы прикладываем силу по высоте балки?вообще запутался

Скорее всего вы имеете в виду рисунок 507 или 149. Объяснения этому даются в соответствующих статьях. Ссылки на них есть в содержании. А вообще лучше начать с самого начала.

Здравствуйте, Доктор Лом! через напряжения или через прогиб то есть перемещение как можно определить момент? и поперечную силу. например я считал какой то программе из объемных элементов не линейным. и там получил нормальные и касательные напряжения и перемещение. и этих данных как можно перейти на внтренные усилия что бы сделать подбор арматуры

Уважаемый доктор Лом. Я полагаю что в формуле 12.3.2 ошибка (результат интегрирования умножен на 2 как в формуле 12.3.3). А так же в описание под этой формулой ссылка на рисунок 11.5 и 11.6, а не на 5.5 и 5.6.

Никакой ошибки нет. Еще раз внимательно посмотрите на формулы, на указанные рисунки и вспомните, как определяется площадь квадратной параболы, если она имеет такой вид, как на рисунке 11.6.

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

Источник