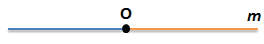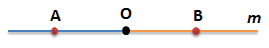Продолжение луча что это
Продолжение луча что это
Построим прямую АВ
(прямая обозначена двумя большими латинскими буквами, например, А и В)
Отметим на прямой АВ точку О
Точка О разбивает прямую АВ на две части (влево от точки О и вправо от точки О)
Части, на которые точка О разбивает прямую АВ, выделены цветом
Каждая из этих частей называется лучом, а точка О является началом одного и другого луча
Назовем получившиеся лучи:
Луч является геометрической фигурой
Луч — это часть прямой, ограниченная с одной стороны
Луч имеет начало, но не имеет конца
Другой способ обозначений
Построим прямую m
(прямая обозначена малой латинской буквой, например, m)
Точка О разбивает прямую m на два луча
Назовем получившиеся лучи
Варианты обозначения лучей
Луч ОВ (обозначение двумя большими латинскими буквами)
Луч ОВ (обозначение двумя большими латинскими буквами)
Луч k (обозначение малой латинской буквой)
Начало луча обозначено буквой О
Луч k (обозначение малой латинской буквой)
Начало луча не обозначено буквой (только отмечено точкой)
Дополнительные лучи
Лучи ОА и ОВ принадлежат одной прямой АВ
Лучи ОА и ОВ имеют общее начало (точка О)
Лучи ОА и ОВ противоположно направлены
При таких условиях лучи ОА и ОВ называются дополнительными
Поделись с друзьями в социальных сетях:
Луч в математике — определение, форма и свойства
Геометрия занимается изучением разных фигур и их свойств. К ним относятся квадрат, треугольник, круг, овал, цилиндр. Луч в математике — это такая прямая, у которой нет конца. Поэтому она считается бесконечной. С данным понятием впервые сталкиваются ученики начальной школы. Более подробно материал изучается в 5 классе. Для решения задач по заданной тематике изучаются плоскость, отрезок, биссектриса.
Трактовка понятий
Впервые термин «луч» использовал в 1833 году швейцарский учёный Якоб Штейнер. Для его определения потребуется на плоскости поставить точку. Из неё должна исходить часть прямой, которая состоит из множества точек, расположенных по одну сторону от первоначальной. Само понятие «точка» считается абстрактным объектом, который не имеет высоты, радиуса, длины, сторон, угла. В задачах важно её местоположение на плоскости либо полуплоскости.
На чертеже она обозначается заглавной латинской буквой. Чтобы различить несколько точек, на рисунке используется несколько букв. Можно вводить числовое обозначение. В отличие от луча, отрезок считается частью прямой, ограниченной двумя точками на концах. Множество точек образует линию, у которой нет толщины и ширины. На плоскости можно начертить следующие её виды:
Линии пересекаются, если имеют одну общую точку. Чтобы они были перпендикулярны друг другу, между ними должен образовываться угол в 90 градусов. При параллельности части прямой не могут скрещиваться.
К особым формам луча относится ломаная. Она состоит из последовательно соединенных отрезков (звенья) под углом, отличным от 180°. Смежные звенья находятся на разных прямых.
У ломаной есть вершины. Они могут обозначаться с помощью латинских заглавных букв. Их нельзя править на маленькие. Сама вершина считается точкой, откуда начинается одна ломаная и заканчивается другая. Основным примером замкнутой линии является многоугольник. Его стороны представлены в виде звеньев.
Описание лучей
В геометрических задачах встречаются дополнительные лучи. Чтобы их начертить, потребуется отобразить на плоскости прямую, разделённую точкой на две полупрямые. Каждая часть является дополнительной относительно другой. Свойства лучей:
Дополнительные лучи могут дополнять друг друга до прямой. Отдельно рассматриваются совпадающие лучи. Если их наложить друг на друга, они совпадут. Для них характерна равная длина.
Чтобы отметить лучи на рисунке, используются порядковые номера.
Незамкнутый открытый луч состоит из точек, находящихся по одну сторону относительно проведённой линии. Для его обозначения используется строчная латинская буква либо две заглавные. Одна точка является началом, а вторая размещается на самом луче. В основе такой фигуры находятся полупрямые. Если в условиях задачи дана линия, формула выглядит следующим образом: (АB). Отрезок записывается в квадратных скобках.
Принципы классификации
Так как луч является частью прямой, поэтому через любую его точку проводится множество прямых, но только через две несовпадающие проходит одна прямая. Луч можно изобразить в нескольких вариантах: пересечение, скрещивание и параллельность.
Чтобы задать луч на плоскости, используется линейное уравнение. Фигуры называются разными способами и с помощью знаков. Можно провести полупрямую «О». Её начальная точка считается исходной и другой не существует. Другой способ записи — использование нескольких букв в середине либо в иных частях линии. Если в задаче дана прямая, её можно обозначить двумя буквами, размещёнными в разных её частях, к примеру, (АB).
Третий метод обозначения: точка «О» находится с некоторым отступом от начала. Центральную часть можно назвать буквой К. В таком случае весь луч будет называться ОК. Если нужно начертить продолжение к прямой, понадобится отметить на чертеже линию и точку, которая будет считаться производной. С помощью последней фигуры делится первая на 2 линии, которые не пересекаются между собой. Чтобы обозначить продолжение, рисуется линия карандашом.
Она будет иметь общее начало с основополагающей, но не будет совпадать с ней. Из т. О проводится прямая, не располагающаяся на дополняющих, но имеющая с ними одно общее начало. На новом луче отмечается т. В. На продолжении лежит отрезок ОВ.
Неразвернутый угол является случаем луча. Если стороны первой фигуры представлены в виде дополнительных полупрямых одной прямой, тогда угол является развёрнутым. Его значение равняется 180 градусов. Если значение угла иное, тогда он неразвернутый.
Следует отличать геометрические лучи от световых.
В математике фигура представлена в виде линии, у которой нет ничего общего с энергией. Для световых лучей характерно несконцентрированное направление, дефракция (переломанный). Но при сильном потоке света наблюдается их чёткое направление.
Аксиомы и доказательства
Свойства лучей определяются аксиомами. Положение 1: на любом луче от начала можно отложить отрезок определённой длины, и только один.
Доказательство: если на линии от начала А отложить 2 равных отрезка АВ и АС, тогда точки С и В совпадут. В и А не лежат на прямой, а находятся с одной стороны от неё. Если отрезок АВ не пересекает эту прямую, тогда множество точек, лежащих с единой стороны от прямой, называется полуплоскостью. При доказательстве положения 1 следует ориентироваться на определение луча.
Аксиома: прямая разделяет плоскость на 2 полуплоскости. Следствие: если D и С находятся в различных полуплоскостях от прямой а, тогда отрезок DC пересекает а. Из этого вытекает теорема: A, B, O, C расположены на прямой а таким образом, что А и В находятся с одной стороны от т. О, т. С и В — с одной стороны от О. При этом А и С размещены с одной стороны от О.
Доказательство: нужно провести через О прямую b, которая отлична от а. Она будет разбивать плоскость на 2 полуплоскости. На одной из них находится т. В. Так как отрезки BC и AB не пересекают прямую b, поэтому точки А и С находятся в одной полуплоскости с В. Отрезок АС не пересекает b. На нём не находится т. О. От неё по одну сторону размещены т. А и С.
Предположение: если O, A, B, C принадлежат прямой а, при этом А находится между В и О, тогда А лежит между О и С. По одну сторону от О находятся три точки А, B и C.
Доказательство: так как по условию т. А находится между О и В, поэтому А и В лежат по одну сторону от О. По второму условию В и С лежат по эту же сторону от О. Исходя из теоремы 1, А, В и С лежат по одну сторону от т. О.
Теорема: если O, A, B, C принадлежат одной линии а, т. А лежит между В и О, а т. В между О и С, тогда В находится между А и С.
Доказательство: выдвигается предположение, что из условия теоремы заключение не следует. Точка В не находится между А и С. По свойству взаиморасположения A, B, C, точки А и С лежат по одну сторону от В. По предположению следует, что они лежат по одну сторону от О, либо A, C, O лежат по одну сторону от B. Это противоречит условию: О и С находятся по разные стороны от В, либо А и С размещены по иную сторону от В, в отличие от т. О.
Подобное противоречит условию принадлежности А отрезку ОВ. Такое противоречие показывает, что предположение о т. В, не лежащей между А и С, неверное. Следовательно, точка В находится между А и С, что доказывает теорему. При решении геометрических задач, связанных с плоскостью и фигурами на ней, учитываются основные теоремы, доказанные учеными за всю историю математики.
Что такое продолжение луча?
Что такое продолжение луча?
В геометрии лучом нарекают часть прямой, у которой есть начало, но нет конца. Луч состоит из точки-начала и всех других точек, которые размещены по одну сторону от данной. Таким образом, одна точка может поделить прямую на два луча. Такие лучи будут величаться дополняющими друг друга.
Продолжением луча величается таковой луч, начало которого совпадает с данным лучом. Но такие два лучи не обязаны совпадать друг с другом
Для того чтоб разобраться что же на самом деле будет продолжением луча обратимся за помощью к прямой.
Чертим дополняющие лучи
Чертим прямую. Дальше необходимо отметить на данной прямой произвольную точку А. В результате, вышла ровная и точка, которая поделила прямую на два луча. Такие лучи стоит считать дополняющими друг друга. Они никогда не пересекутся и имеют одно единственное начало в одной точке. В точке А.
Чертим продолжение луча
По определению продолжение луча это таковой луч, который имеет общее начало, но не совпадает с имеющимся лучом. То есть дополняющие лучи также нельзя именовать продолжением луча. Для того чтоб выстроить по данному чертежу продолжение луча нужно провести из точки А таковой луч, который не будет размещен на дополняющих лучах, а будет иметь с ними общее начало в точке А. Начертили и отметили на нём точку В. Отрезок АВ лежит на продолжении луча из точки А.
Продолжение луча что это
Луч — это часть прямой линии, расположенная по одну сторону от любой точки, лежащей на этой прямой. Луч также называется полупрямой.
Любой луч имеет начало и направление. Начало луча, начальная точка или вершина луча — это точка, из которой исходит луч. Таким образом, у луча есть начало, но нет конца.
Рассмотрим три луча с общим началом:
Дополнительные лучи
Любая точка, лежащая на прямой линии, делит эту прямую на две полупрямые, то есть на две части. Каждая из этих частей будет называться дополнительным лучом относительно второго луча:
Дополнительные лучи — это лучи, имеющие общее начало, противоположные направления и лежащие на одной прямой. Также можно сказать, что дополнительными называются лучи, дополняющие друг друга до прямой линии.
Обозначение лучей
Луч обозначают одной строчной латинской буквой:
Также луч можно обозначить двумя точками, лежащими на нём:
При обозначении луча двумя точками, на первом месте ставится буква, обозначающая начало луча, а на втором — буква, обозначающая какую-либо другую его точку: луч BC.
Посмотрим на следующий пример:
Луч с началом в точке A можно обозначить как AB или AC.
Что такое продолжение луча?
Ответ или решение 2
В геометрии лучом называют часть прямой, у которой есть начало, но нет конца. Луч состоит из точки-начала и всех остальных точек, которые расположены по одну сторону от данной. Таким образом, одна точка может разделить прямую на два луча. Такие лучи будут называться дополняющими друг друга.
Продолжением луча называется такой луч, начало которого совпадает с данным лучом. Но такие два лучи не должны совпадать друг с другом
Для того чтобы разобраться что же на самом деле будет продолжением луча обратимся за помощью к прямой.
Чертим дополняющие лучи
Чертим прямую. Далее необходимо отметить на данной прямой произвольную точку А. В результате, получилась прямая и точка, которая разделила прямую на два луча. Такие лучи стоит считать дополняющими друг друга. Они никогда не пересекутся и имеют одно единственное начало в одной точке. В точке А.
Чертим продолжение луча
По определению продолжение луча – это такой луч, который имеет общее начало, но не совпадает с имеющимся лучом. То есть дополняющие лучи также нельзя назвать продолжением луча. Для того чтобы построить по данному чертежу продолжение луча необходимо провести из точки А такой луч, который не будет расположен на дополняющих лучах, а будет иметь с ними общее начало в точке А. Начертили и отметили на нём точку В. Отрезок АВ лежит на продолжении луча из точки А.