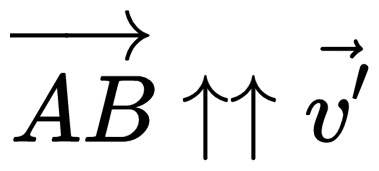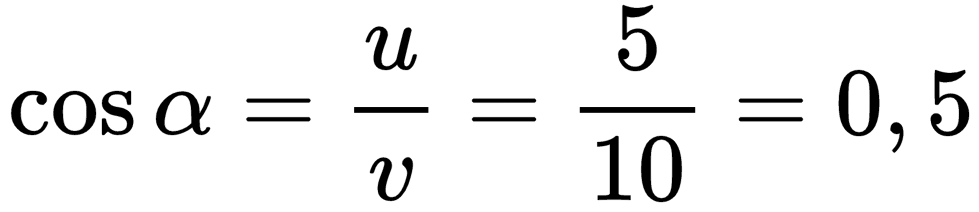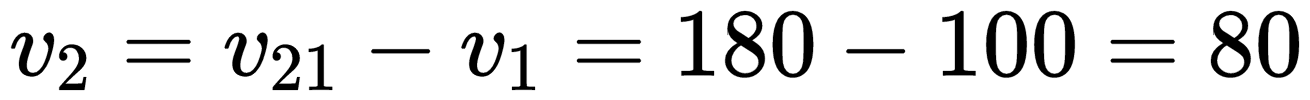Приведите примеры показывающие что механическое движение действительно относительно
Механическое движение. Относительность механического движения
Механическое движение. Относительность механического движения
Данная статья написана в целях подготовки к ЕГЭ по физике, статья содержит в себе описание раздела кинематики по физике, с подробным разбором примеров задач. Изучив данный материал вам не составит труда решать такие задания на ЕГЭ по физике, так как вы будете знакомы с данной темой.
Переходим к рассмотрению темы. Начнём с понятия о механическом движении.
Понятие механического движения означает изменение расположения тела по отношению других тел с промежутком определённого времени.
Самое понятие движение общее, оно охватывает широкий спектр различных явлений. В физике обычно изучают разные виды движения. Самым простым считают механическое.
Рассмотрим пример: тело C изменяет положение с телом О, в данном случае тело О также будет менять своё положение в соответствии с С. Механическое движение принять считать относительным, то есть если его описать, следует указывать в соответствии с каким телом его рассматривают. Примером является едущий по рельсам поезд, он движется по рельсам, значит, пассажир движется относительно данного поезда.
Телом отсчёта называют тело, в соответствии с котором рассматривают движение.
Основной задачей механики является определение расположения тела, которое движется в любое время. Для того, чтобы решать подобные задачи, движение нужно представлять в качестве изменения координат в течение времени. Для того, чтобы определить координаты, понадобится система координат, для времени – часы. То есть систему отсчёта составляют время и координаты.
Рассмотрим пример на рисунке (рис. 1).
Здесь OM является радиусом и вектором точки М. Х, у, z. Точка М служит координатой радиуса, то есть вектора.
Решением задачи будет найти точку М и её координаты, при это х = х ( t ), y = y ( t ), z = z ( t ).
Итак, рассмотрим понятие материальной точки: тело, массой и размерами которого можно пренебречь в решении задачи.
Например, поезд будет являться материальной точкой в процессе движения, когда поезд будет останавливаться, он не будет считаться материальной точкой.
Основными характеристиками движения являются:
Рассмотри каждую характеристику более подробно.
Траекторией называют линию, относительно которой тело движется.
Путь – размер траектории, которую проходит тело в процессе движения за определённый промежуток времени.
Под перемещением понимают вектор, который соединяет положение тела в начале и в конце движения.
Относительность механического движения
В КИМах задачи на движение ЕГЭ по физике встречаются довольно часто. Перейдём к рассмотрению данного раздела.
Движение тела относительно других тел является разным. Рассмотрим пример, едущего с пассажирами автобуса. Пассажиры двигаются вместе с автобусом, то есть они передвигаются относительно пути, при этом, пассажиры не движутся относительно автобуса. В этом примере рассмотрена относительность движения.
Для того, чтобы описать движение тел, следует учитывать по отношению к чему рассматривать данное движение. В этом случае тело является точкой отсчёта. Также относительным будет покой. Например, пассажир, едущий в электричке, увидев встречную, не может чётко понять какая из них движется. Для определения он будет смотреть на землю либо на небо.
Во вселенной не существует тел, которые всегда в абсолютном покое. Определить движение тело можно в соответствии с движением другого тела.
Таким образом, с различных взглядов движение одного тела можно видеть по-разному. Для них скорость тела и направление самого движения также будет выглядеть по-разному.
Для наглядности решим задачу по данной теме. В условии сказано, что две электрички, едущие навстречу друг другу, имеют скорости 70 км / ч и 60 км / ч. Пассажир одной электрички утверждаем, что вторая ехала мимо него в течение 14 секунд.
Найти: длину электрички.
Решение: V1 = 72 км / ч, V2 = 54 км / ч, t2 = 14 c. СИ: 20 м / с, 15 м / с.
Следует выбрать неподвижную систему координат, например, линейную. Система отсчёта для второго поезда перемещается V1 = — 20 м / с, поезд двигается со скоростью 15 м / с.
V = — 20 м / с – 15 м / с = — V1 + ( — V2 ).
V = — 20 м / с – 15 м / с = — 25 м / с.
I2 = 25 м / с * 14 м / с = 350 м.
Ответ: 350 метров длина поезда.
Система отсчёта
В физике само определение системы включает в себя следующие критерии:
Движение материальной точки изучается в соответствии с данными критериями.
Обычно в физике все виды движения рассматривают как относительные. То есть любое движение рассматривают по отношению к другому телу, как было сказано выше. Например, узнать о движении Луны можно относительно созвездий, Солнца и так далее. Такие тела отсчёта будут составлять координаты.
Итак, рассмотрим составляющие систем отсчёта:
— Тело отсчёта – тело, в соответствии с которым можем выяснить изменение в движении других тел;
— Время – промежуток времени, который необходим для определения нахождения тела.
Тело отсчёта можно выбрать произвольно. Нужно учитывать, что при этом равноправными являются тело, которое движется и само тело отсчёта. Любое из них следует рассматривать как тело отсчёта либо в качестве движущегося тела.
Рассмотрим пример решения задач.
Скорость ветра – 30 м / с, скорость автобуса равна 110 км / ч. Как должен двигаться автобус, для того чтобы находиться в покое.
Решение: Скорость автобуса должна быть равно скорости ветра, в этом случае он будет в состоянии покоя. Для сравнения скорости автобуса с ветром выразим: 30 м / с * ( 3600 / 1000 ) км / ч = 108 км / ч.
Ответ: из этого следует, что автобус со скоростью 110 км / ч имеет возможность двигаться так, чтобы быть в покое с ветром.
Для решения задач на подобные темы ЕГЭ физике базового уровня следует выбрать соответствующую систему координат.
В физике рассматривают несколько систем:
Рассмотрим инерциальные системы отсчёта. Инерциальной называют такую систему, в которой тело будет находиться в покое в случае, если на него не оказывают влияние другие силы. Здесь на тело оказывает воздействие инерция. В этой системе отсчёта можно более простым способом описать движение разных тел.
Неинерциальными системами считают системы, движущиеся относительно инерциальной.
Все неинерциальные системы связаны с планетой Земля. Отличительная черта неинерциальной системы – перемещение с ускорением в соответствии с инерциальной системой. В данной ситуации известные законы Ньютона требует применения дополнительных переменных. Без них описание системы отсчёта будет не достаточно правдивым. Неинерциальная система требует рассмотрения на примерах. Так как у рассматриваемых тел непростая траектория движения. Хорошим примером является движение планет. Коперник впервые изучил неинерциальное движение. Он установил, что движение нескольких тел является сложным. Ранее движение нашей планеты считали инерциальным и описывали с применением законов Ньютона.
Данный материал предназначен для самостоятельной подготовки с нуля к сдаче единого государственного экзамена по физике. Изучив его, просмотрев примеры и дополнительно порешав задачи на рассмотренные темы, вы сможете без затруднений решить их на ЕГЭ.
Относительность механического движения
теория по физике 🧲 кинематика
Под относительностью понимают зависимость чего-либо от выбора системы отсчета. Так, покой и движение тела, его положение в пространстве всегда относительны. Человек, сидящий внутри движущегося автомобиля, покоится относительно этого автомобиля. Но относительно предметов снаружи он движется с некоторой скоростью.
Относительность перемещения
Чтобы применять правило сложения перемещений, нужно уметь складывать вектора.
Пример №1. Человек прошел в автобусе 2 метра в направлении заднего выхода. За это же время автобус успел переместиться относительно остановки на 10 м. Найти перемещение человека относительно автобусной остановки.
Так как человек двигался в сторону конца автобуса, он двигался противоположно его движению. В этом случае его перемещение будет равно модулю разности перемещений, совершенных человеком относительно автобуса и автобусом относительно остановки:
Относительность скорости в ПСО и НСО
Складывая векторы скоростей, нужно пользоваться правилами сложения векторов.
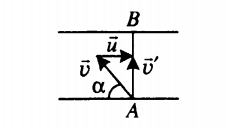
Пример №2. Моторная лодка должна пересечь реку, скорость течения которой равна 5 км/ч, по кратчайшему пути. Собственная скорость лодки равна 10 км/ч. Определить, под каким углом к берегу должна быть направлена лодка, чтобы она не отклонялась от кратчайшего пути.
Кратчайшим путем между двумя параллельными линиями является отрезок, заключенный между этими линиями при условии, что он лежит на прямой, пересекающей эти линии под прямым углом. На рисунке этот путь отметим отрезком АВ.
Лодка движется прямолинейно. Поэтому направление ее скорости относительно берега совпадает с направлением перемещения:
Векторы скоростей образуют прямоугольный треугольник, и собственная скорость лодки направлена к берегу под некоторым углом α. Косинус этого угла равен отношению прилегающего катета (скорости лодки относительно реки) к гипотенузе (скорости течения реки):
Косинусу 0,5 соответствует угол, равный 60 градусам.
Относительная скорость двух тел
Понятие относительной скорости вводится, когда рассматривается движение двух тел относительно друг друга внутри одной и той же системы отсчета (СО). Примером служат два движущихся автомобиля, в то время как их движение рассматривается относительно неподвижного объекта.
Относительная скорость равна векторной разности скоростей первого и второго тела относительно СО:
v отн — относительная скорость, или скорость первого тела относительно второго, v 1 и v 2 — скорость первого и второго тела относительно СО.
Варианты обозначения относительной скорости и их проекций:
Для вычисления относительной скорости движения тела важно уметь применять правила вычитания векторов.
Пример №3. Два автомобиля движутся противоположно друг другу. Скорость первого автомобиля относительно дороги равна 100 км/ч. Скорость второго автомобиля относительно первого равна 180 км/ч. Найти модуль скорости второго автомобиля относительно дороги.
Так как автомобили движутся в противоположном направлении, относительная скорость равна сумме скоростей первого и второго автомобиля. Поэтому скорость второго равна разности относительной скорости и скорости движения второго тела, которым в данном случае является первый автомобиль:
Скорость второго автомобиля относительно дороги равна 80 км/час.
Правила сложения векторов
| Сложение двух сонаправленных векторов | |
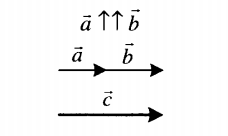 | Суммой двух сонаправленных векторов является вектор, направленный в ту же сторону. Его длина равна сумме длин слагаемых векторов: c = a + b. |
| Сложение двух противоположно направленных векторов | |
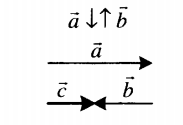 | Суммой двух противоположно направленных векторов является вектор, направленный в сторону большего по модулю вектора. Его длина равна модулю разности длин слагаемых векторов: c = |a – b|. |
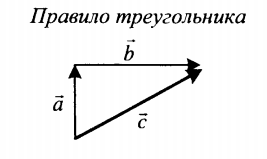
| Сложение двух векторов, расположенных друг к другу под углом | |
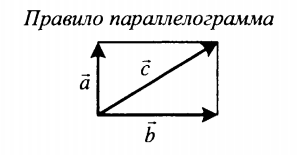
| Суммой двух векторов, расположенных друг к другу под углом является вектор, направление которого определяется графически методом треугольника или параллелограмма. Его длина зависит от величины угла, под которым расположены два слагаемых векторов. | |
 | Если слагаемые векторы перпендикулярны, для вычисления длины вектора их суммы используется теорема Пифагора: 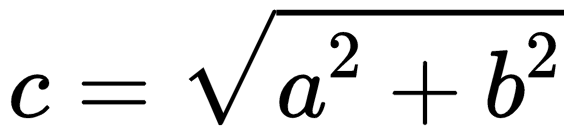 . . |
 | |
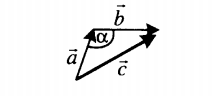 | Если слагаемые векторы расположены под тупым углом α, для вычисления длины вектора их суммы используется теорема косинусов: 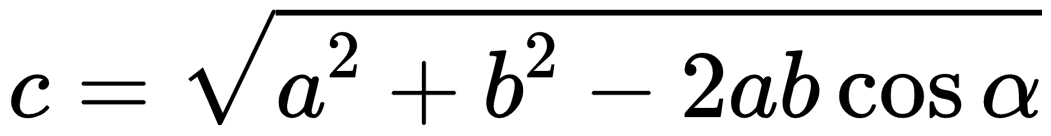 . . |
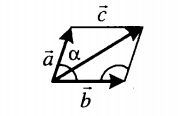 | Если слагаемые векторы расположены под острым углом α, для вычисления длины вектора их суммы используется теорема косинусов: 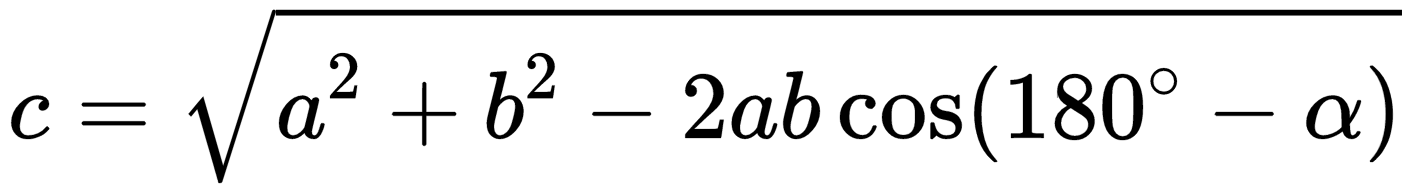 . . |
Правила вычитания векторов
Эта таблица иллюстрирует правила вычитания векторов на примере векторов 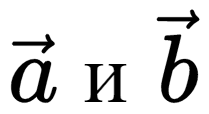
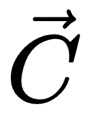
Алгоритм решения
Решение
Записываем данные относительно Земли:
Изображаем графическую модель ситуации. Так как у второго автомобиля перед вектором скорости стоит знак «–», первый и второй автомобили движутся во взаимно противоположных направлениях.
Записываем закон сложения скоростей в векторном виде:
v ′ — скорость второго автомобиля относительно оси ОХ ( v 2), v — скорость второго автомобиля относительно системы отсчета, связанной с первым автомобилем, u — скорость движения первого автомобиля относительно оси ОХ ( v 1).
Закон сложения скоростей в векторном виде применительно к условиям задачи будет выглядеть так:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Записываем закон сложения скоростей в векторном виде:
v ′ — скорость автомобиля относительно земли ( v 1), v — скорость второго автомобиля относительно системы отсчета, связанной со вторым автомобилем, u — скорость движения второго автомобиля относительно земли ( v 2). По условию задачи в качестве системы отсчета нужно выбрать второй автомобиль. Так как система отсчета, связанная со вторым автомобилем, и первый автомобиль движутся в одном направлении, классический закон сложения скоростей в скалярном виде будет выглядеть так:
Отсюда скорость первого автомобиля в системе отсчёта, связанной со вторым автомобилем:
По условию задачи ответом должен быть модуль этой скорости. Модуль числа 50 есть 50.Ответ: 50
pазбирался: Алиса Никитина | обсудить разбор | оценить
Механическое движение и его характеристики
теория по физике 🧲 кинематика
Механика — раздел физики, который изучает механическое движение физических тел и взаимодействие между ними.
Основная задача механики — определение положение тела в пространстве в любой момент времени.
Механическое движение — изменение положения тела в пространстве относительно других тел с течением времени.
Механическое движение и его виды
По характеру движения точек тела выделяют три вида механического движения:
По типу линии, вдоль которой движется тело, выделяют два вида движения:
По скорости выделяют два вида движения:
По ускорению выделяют три вида движения:
Что нужно для описания механического движения?
Для описания механического движения нужно выбрать, относительно какого тела оно будет рассматриваться. Движение одного и того же объекта относительно разных тел неодинаковое. К примеру, идущий человек относительно дерева движется с некоторой скоростью. Но относительно сумки, которую он держит в руках, он находится в состоянии покоя, так как расстояние между ними с течением времени не изменяется.
Решение основной задачи механики — определения положения тела в пространстве в любой момент времени — заключается в вычислении координат его точек. Чтобы вычислить координаты тела, нужно ввести систему координат и связать с ней тело отсчета. Также понадобится прибор для измерения времени. Все это вместе составляет систему отсчета.
Система отсчета — совокупность тела отсчета и связанных с ним системы координат и часов.
Тело отсчета — тело, относительно которого рассматривается движение.
Часы — прибор для отсчета времени. Время измеряется в секундах (с).
При описании движения тела важно учитывать его размеры, так как характер движения его отдельных точек может различаться. Но в рамках некоторых задач размер тела не влияет на результат решения. Тогда его можно считать пренебрежительно малым. Тогда тело рассматривают как движущуюся материальную точку.
Материальная точка — это тело, размерами которого можно пренебречь в условиях конкретной задачи. Допустимо принимать тело за точку, если оно движется поступательно или его размеры намного меньше расстояний, которые оно проходит.
Виды систем координат
В зависимости от характера движения тела для его описания выбирают одну из трех систем координат:
Способы описания механического движения
Описать механическое движение можно двумя способами:
Координатный способ
Указать положение материальной точки в пространстве можно, используя трехмерную систему координат. Если эта точка движется, то ее координаты с течением времени меняются. Так как координаты точки зависят от времени, можно считать, что они являются функциями времени. Математически это записывается так:
Эти уравнения называют кинематическими уравнениями движения точки, записанными в координатной форме.
Векторный способ
Радиус-вектор точки — вектор, начало которого совпадает с началом системы координат, а конец — с положением этой точки.
Указать положение точки в трехмерном пространстве также можно с помощью радиус-вектора. При движении точки радиус-вектор со временем изменяется. Он может менять направление и длину. Это значит, что радиус-вектор тоже можно принять за функцию времени. Математически это записывается так:
Эта формула называется кинематическим уравнением движения точки, записанным в векторной форме.
Характеристики механического движения
Движение материальной точки характеризуют три физические величины:
Перемещение
Траектория — линия, которую описывает тело во время движения.
Путь — длина траектории. Обозначается буквой s. Единица измерения — метры (м).
Путь есть функция времени:
Модуль перемещения — длина вектора перемещения. Обозначается как |Δ r |. Единица измерения — метры (м).
Модуль перемещения необязательно должен совпадать с длиной пути.
Пример №1. Человек обошел круглое поле диаметром 1 км. Чему равны пройденный путь и перемещение, которое он совершил.
Путь равен длине окружности. Поэтому:
Человек, обойдя круглое поле, вернулся в ту же точку. Поэтому его начальное положение совпадает с конечным. В этом случае человек совершил перемещение, равное нулю.
Пример №2. Точка движется по окружности радиусом 10 м. Чему равен путь, пройденный этой точкой, в момент, когда модуль перемещения равен диаметру окружности?
Диаметр — это отрезок, который соединяет две точки окружности и проходит через центр. Перемещение равно длине этого отрезка в случае, если один из концов этого отрезка является началом вектора перемещения, а другой — его концом. Траекторией движения в этом случае является дуга, равная половине окружности. А длина траектории есть путь:
Скорость
Скорость — векторная физическая величина, характеризующая быстроту перемещения тела. Численно она равна отношению перемещения за малый промежуток времени к величине этого промежутка.
Скорость характеризуется не только направлением вектора скорости, но и его модулем.
Модуль скорости — расстояние, пройденное точкой за единицу времени. Обозначается буквой V и измеряется в метрах в секунду (м/с).
Математическое определение модуля скорости:
Величина скорости тела в данный момент времени есть первая производная от пройденного пути по времени:
Ускорение
Ускорение — векторная физическая величина, которая характеризует быстроту изменения скорости тела. Численно она равна отношению изменения скорости за малый промежуток времени к величине этого промежутка.
Модуль ускорения — численное изменение скорости в единицу времени. Обозначается буквой a. Единица измерения — метры в секунду в квадрате (м/с 2 ).
Математическое определение модуля скорости:

Ускорение тела есть первая производная от скорости или вторая производная от пройденного пути по времени:
Проекция вектора перемещения на ось координат
Проекция вектора перемещения на ось — это скалярная величина, численно равная разности конечной и начальной координат.
Проекция вектора на ось OX:
Проекция вектора на ось OY:
Знаки проекций перемещения
Проекция вектора перемещения на ось считается нулевой, если вектор расположен перпендикулярно этой оси.
Модуль перемещения — длина вектора перемещения:
Модуль перемещения измеряется в метрах (м).
Вместе с собственными проекциями модуль перемещения образует прямоугольный треугольник. Сам он является гипотенузой этого треугольника. Поэтому для его вычисления можно применить теорему Пифагора. Выглядит это так:
Выразив проекции вектора перемещения через координаты, эта формула примет вид:
Выражение проекций вектора перемещения через угол его наклона по отношению к координатным осям:
Общий вид уравнений координат:
Пример №3. Определить проекции вектора перемещения на ось OX, OY и вычислить его модуль.
Определяем координаты начальной точки вектора:
Определяем координаты конечной точки вектора:
Проекция вектора перемещения на ось OX:
Проекция вектора перемещения на ось OY:
Применяем формулу для вычисления модуля вектора перемещения:
Пример №4. Определить координаты конечной точки B вектора перемещения, если начальная точка A имеет координаты (–5;5). Учесть, что проекция перемещения на OX равна 10, а проекция перемещения на OY равна 5.
Извлекаем известные данные:
Для определения координаты точки В понадобятся формулы:
Выразим из них координаты конечного положения точки:
Точка В имеет координаты (5; 10).
Алгоритм решения
Решение
Записываем исходные данные:
Записываем формулу ускорения:
Так как начальная скорость равна 0, эта формула принимает вид :
Отсюда скорость равна:
Подставляем имеющиеся данные и вычисляем:
pазбирался: Алиса Никитина | обсудить разбор | оценить