Приблизительно равно что значит
Как поставить знак приблизительно равно в Word и Excel
На клавиатуре отсутствует знак приблизительного равенства, а для вставки часто применяют копирование из другого места. Но есть и более удобные способы, которые помогут быстро напечатать символ в любом месте документа Word или Excel.
Конвертация кода в знак
Первый способ заключается в конвертации юникода символа в знак. В любом месте документа набираем 2248 и одновременно нажимаем «Alt» + «X».
Вторая возможность связана с ASCII-кодом и преобразование идёт следующим чередом:
Оба варианта работают в Word, Excel и других офисных программах.
Вставка символа без клавиатуры
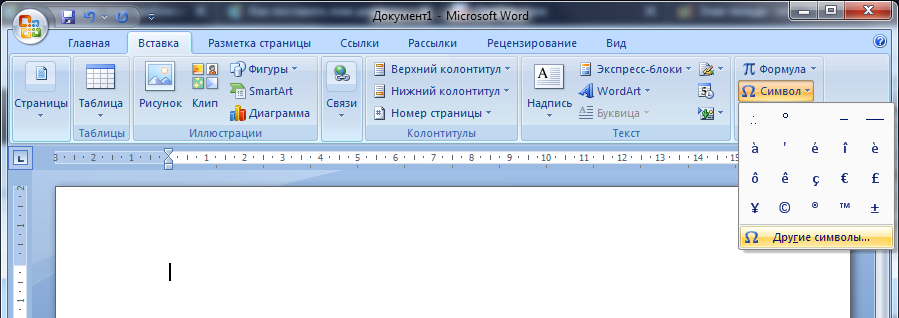
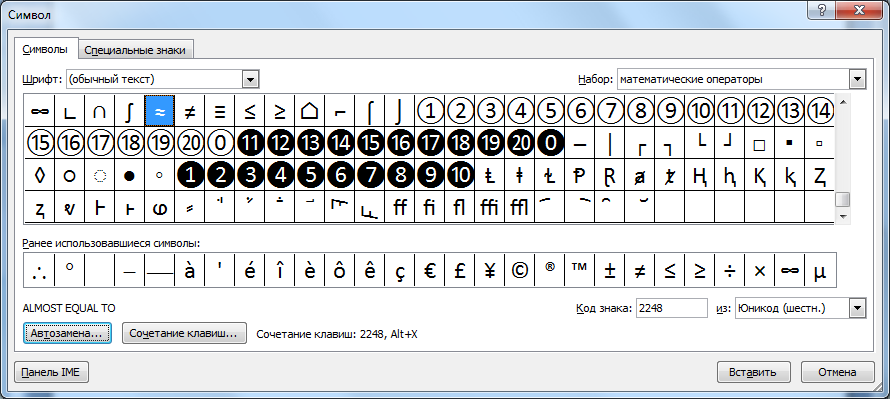
В Word для вставки символа приблизительно равно можно воспользоваться функцией вставки. На вкладке «Вставка» открываем окно «Другие символы».
Выбираем шрифт «обычный текст» и набор «математические операторы». В первых рядах будет нужный знак.
Похожие знаки равенства
Кроме знака примерного равенства есть много похожих математических и геометрических операндов. Они часто используются в формулах и имеют разную смысловую нагрузку.
эквивалентность22868764≅конгруэнтность22458773
К ним также применимы способы вставки в офисных программах.
Равенство и неравенство. Знаки: больше, меньше, равно
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Математические знаки
Скорее всего, к первому классу ребенок уже отличает на слух и визуально, что горстка из десяти ягод больше трех штук. Чтобы внедрить в жизнь новые обозначения, посмотрим на знаки «больше», «меньше», «равно» в картинках.
Символ больше (>) — это когда острый нос галочки смотрит направо. Его нужно использовать, когда первое число больше второго:
Символ меньше (
Символ равенства (=) — это когда два коротких отрезка записаны горизонтально и параллельны друг другу. Используем его при сравнении двух одинаковых чисел:
Чтобы ребенку было легче запомнить схожие между собой знаки, можно применить игровой метод. Для этого нужно сравнить числа и определить в каком порядке они стоят. Далее ставим одну точку у наименьшего числа и две — рядом с наибольшим. Соединяем точки и получаем нужный знак. Вот так просто:
Равенство и неравенство
Что такое равенство в математике — это когда одно подобно по количеству другому и между ними можно поставить знак =.
Для примера посмотрим на картинку с изображением геометрических фигур. Справа и слева количество одинаковое, значит можно поставить символ «равно».
Наглядный пример неравенства изображен на картинке ниже. Слева видим три фигуры, а справа — четыре. При этом мы знаем, что три не равно четырем или еще так: три меньше четырех.
Урок в школе зачастую проходит перед учебником, тетрадью и доской. Дома же можно использовать компьютер и некоторые задания выполнять в онлайн-формате. Как найти знаки на клавиатуре? Ответ на картинке:
Типы неравенств
Знак примерно (приблизительно) на клавиатуре: как поставить на компьютере или ноутбуке?
Общая характеристика
Главная задача знаков — описание этапов осуществляемых действий. Математическое уравнение или выражение имеет одиночную пару квадратных, фигурных и других скобок, а также может использовать их некоторое количество.
Значение и разновидности
Скобки — это парные знаки, используемые во всевозможных областях. Чтобы правильно выстроить фразу в русском языке, для понимания смысла текста в предложении они употребляются как знаки препинания. С начальных классов школы изучают основы этих знаков.
В расчетах первая из скобок считается открывающей, а вторая — замыкающей. Оба знака соответствуют друг другу, но также используются те, в которых открытие или закрытие не различается (косые /…/, прямые скобки |…|, двойные прямые ||…||. Раскрывать значение можно чаще всего в математике, физике, химии и остальных науках для указания важности выполнения операции в формулах. На компьютерной клавиатуре представлены все виды знаков препинания.
Разновидности:
Открытие круглых () произошло в 1556 году для подкоренного выражения. По правилу первым выполняется действие внутри знака, затем произведение или определение частного (деление), а в конце — суммирование и разница.
В Microsoft word, Excel включена электронная конфигурация этих знаков. Часто используемые виды скобок, следующие: (), [ ], < >(), [ ], < >. Также встречаются двойные, называемые обратными (]] и [ [) или > в виде уголка. Их использование является двойственным — с открывающейся и замыкающей скобочкой.
Основные цели квадратной скобки в математике:
Другие варианты расчета:
Квадратные скобки в математике обозначают, что действие выполняется последовательно. Эти знаки позволяют разграничить операции.
Треугольные актуальны в теории групп. Правило записи ⟨ a ⟩ n характеризует циклическую группу порядка n, сформированную элементом a.
Круглые (операторные) () используются в математике для описания первостепенности действий. Например, (1 +5)*3 означает, что нужно сначала сложить 1 и 5, а затем полученную величину перемножить на 3. Наряду с квадратными, используются для записи разных компонент векторов, матриц и коэффициентов.
На уроке математики преподаватель объясняет, как раскрыть скобки в уравнении для последующего решения. Фигурная одинарная < встречается при решении систем уравнений, обозначает пересечение данных, а [[ используется при их слиянии.
Одинарные или двойные выражения
Употребление [] происходит реже. Одно уравнение со скобками объединяет несколько значений или неравенств различных размеров. Для решения совокупности нужно выполнить любое условие. Конец, завершение действия замыкает закрывающий знак.
В персональных компьютерах, ноутбуках, нетбуках встроена кодировка Юникод, закрепленная не за левыми или правыми объединяющими знаками, а за открывающими и замыкающими, поэтому при воспроизведении печатного текста со скобочками в режиме «справа налево» каждый знак меняет внешнее направление на обратное.
Квадратные скобки в уравнении означают, что установлен порядок действий, задаются границы промежутков и необходимость выполнения действия над выражением. Двойные квадратные скобки необходимы для записи выражений наряду с круглыми для рационального порядка действий.
По правилам интервал [−a;+a] записывается в виде нестрогого неравенства −a≤x≤a, означающего, что x находится на промежутке от −a до a включительно.
В середине парного знака с отделяющей точкой или запятой указываются два числа — наименьшее, затем большее, ограничивающие интервал. Круглая скобочка, прилегающая к цифре, означает невключение числа в промежуток, а квадратная — добавление.
В некоторых учебных пособиях для вузов встречаются расшифровки числовых интервалов, в которых вместо круглой скобочки (применяется обратная квадратная скобка ], и наоборот. В обозначениях запись ]0, 1[ равносильна (0, 1).
Открытая квадратная скобка (символ [) значит, что совокупность представляет систему уравнений разных размеров, для которых справедливы все множества решений для каждого уравнения, входящего в общее задание. Например, [x+11=2yy2−12=0
Прежде чем решать задачу или выполнять задание, нужно правильно определить принципы действий. В некоторых случаях скобочки могут быть не нужны, а иногда их обязательно нужно поставить.
Фигурные скобки
В вики-разметке двойные фигурные скобки применяются для шаблонов.
Использование круглых скобок в математике
Круглые скобки в математике встречаются наиболее часто, и они используются для множества целей.
Первое применение.
С помощью круглых скобок устанавливается порядок действий для вычисления алгебраического выражения. Выражение, которое стоит в скобках, вычисляется первым, за ним следует вычисление всех остальных.
В случае же если в выражении скобок много и одна находится внутри другой — первыми вычисляются скобки с максимальной глубиной вложенности.
Готовые работы на аналогичную тему
Второе применение.
Третье применение.
Круглые скобки также используются для обозначения действий, которые необходимо совершить над всем выражением, стоящим в скобках. Под действием здесь имеются в виду возведение в степень, взятие производной или вычисление подинтегрального выражения.
$(x+2)^2; int_1^5 (x^2+5x)dx; f’(x)= (5x^2 + 1)’$
Четвёртое применение.
Пятое применение.
Пятое применение.
Угловые скобки
В квантовой механике угловые скобки используются в качестве так называемых бра и кет (от англ. bracket — скобка), введённых П. А. М. Дираком для обозначения квантовых состояний (векторов) и матричных элементов. При этом квантовые состояния обозначаются как 


Кроме того, в физике угловыми скобками обозначают усреднение (по времени или другому непрерывному аргументу), например, 
В текстологии и издании литературных памятников угловыми скобками обозначают лакуны в тексте — 
Второй способ
Если вам нужны исключительно две волнистые черты, их тоже можно поставить, но способ чуть более долгий.
На клавиатуре своего устройства нажмите Win+R.
Появится окно «Выполнить». Добавьте команду charmap.exe, нажмите ОК.
Запущена таблица символов Windows.
Выбираете шрифт Arial, затем в списке находите символ приблизительно (примерно), нажимаете на него левой клавишей мыши, а затем по очереди — на кнопки «Выбрать» и «Копировать».
Теперь вставляете символ в определенное место вашего текста.
Вставка символа без клавиатуры
В Word для вставки символа приблизительно равно можно воспользоваться функцией вставки. На вкладке «Вставка» открываем окно «Другие символы».
Выбираем шрифт «обычный текст» и набор «математические операторы». В первых рядах будет нужный знак.
Конвертация кода в знак
Первый способ заключается в конвертации юникода символа в знак. В любом месте документа набираем 2248 и одновременно нажимаем «Alt» + «X».
Вторая возможность связана с ASCII-кодом и преобразование идёт следующим чередом:
Оба варианта работают в Word, Excel и других офисных программах.
Первый способ
Скажем сразу — для этого способа мы будем использовать символ тильда в виде одной волнистой черты, в то время как в знаке приблизительно черты две. Тем менее, тильду часто используют в качестве символа примерно, так что проблем быть не должно.
Используйте англоязычную раскладку. Если используется русскоязычная, переключите ее, нажав Shift+Ctrl:
Или используйте языковую иконку, которая находится на панели задач:
Теперь найдите символ тильды (слева от цифры 1, часто на этой же клавише можно увидеть букву ё).
Однако если нажать на указанную клавишу, вы увидите совсем другой символ, поэтому предварительно нажмите на Shift и, удерживая его, нажмите на клавишу тильда, после чего отпустите Shift.
Что у вас должно получиться:
Квадратные скобки в математике
Что же означают квадратные скобки в математике и для чего они используются?
Квадратные скобки в математике встречаются реже чем круглые, но всё же их можно встретить довольно часто.
Первое применение.
Квадратные скобки иногда используются при записи выражений наряду с круглыми для того, чтобы было проще различить скобки и, соответственно, задаваемый ими порядок действий. Часто с такой целью квадратные скобки используются для записи формул физики и других технических наук.
$[(5+2) cdot 2] cdot(25-3+(-5))$
Второе применение.
Третье применение.
С помощью квадратной скобки записывают совокупности. Совокупности — это системы уравнений, для которых справедливы все множества решений для каждого уравнения, входящего в совокупность.
$left [ begin
Круглые скобки
Используются в математике для задания приоритета математических и логических операций. Например, (2+3)·4 означает, что надо сначала сложить 2 и 3, а затем сумму умножить на 4; аналогично выражение 


для записи биномиальных коэффициентов :
Круглые скобки в математике используются также для выделения аргументов функции: 
(здесь приведены три различных варианта написания, встречающиеся в литературе) и смешанное (тройное скалярное) произведение :
Скобки (обычно круглые, как в этом предложении) употребляются в качестве знаков препинания в естественных языках.
В ЮникодеU + 003D = ЗНАК РАВНО (HTML = · = )СвязанныйСмотрите такжеU + 2260 ≠ НЕ РАВНОU + 2248 ≈ ПОЧТИ РАВНО
U + 2261 ≡ ИДЕНТИЧНО
СОДЕРЖАНИЕ
История
Этимология слова «равный» происходит от латинского слова « æqualis», означающего «равномерный», «идентичный» или «равный», от aequus («уровень», «даже» или «справедливый»).
Использование в математике и компьютерном программировании
Несколько знаков равенства
Другое использование
Написание
Тон письма
Личные имена
Вместо двойного дефиса в японском языке иногда используется знак равенства в качестве разделителя между именами. В оджибве легко доступный знак равенства на клавиатуре используется вместо двойного дефиса.
Лингвистика
В лингвистических подстрочных глоссах для обозначения границ клитики обычно используется знак равенства: знак равенства ставится между клитикой и словом, к которому она прикреплена.
Химия
Символ ЛГБТ
Язык вражды
Символ неравенства (≠) был принят некоторыми сторонниками превосходства белой расы и другими расистскими группами.
Использование в телеграммах и телексе
Связанные символы
Примерно равно
Символы, используемые для обозначения примерно одинаковых предметов, включают следующее:
Не равный
Символ, используемый для обозначения неравенства (когда элементы не равны), представляет собой косой знак равенства ≠ (U + 2260). В LaTeX это делается с помощью команды «\ neq».
Личность
Изоморфизм
Символ ≅ часто используется для обозначения изоморфных алгебраических структур или конгруэнтных геометрических фигур.
В логике
Другие связанные символы
Дополнительные символы в Юникоде, связанные со знаком равенства, включают:
Неправильное использование
Знак равенства иногда используется неправильно в математическом аргументе, чтобы соединить шаги математики нестандартным способом, а не для того, чтобы показать равенство (особенно ранними учениками математики).
Например, если кто-то шаг за шагом находил сумму чисел 1, 2, 3, 4 и 5, можно было бы неправильно написать:
1 + 2 = 3 + 3 = 6 + 4 = 10 + 5 = 15.
Структурно это сокращение для:
([(1 + 2 = 3) + 3 = 6] + 4 = 10) + 5 = 15,
но обозначение неверно, потому что каждая часть равенства имеет разное значение. Если интерпретировать строго так, как говорится, это будет означать, что:
Правильная версия аргумента:
1 + 2 = 3, 3 + 3 = 6, 6 + 4 = 10, 10 + 5 = 15.
Эта трудность возникает из-за тонких различий в использовании знака в образовании. В ранних оценках, ориентированных на арифметику, знак равенства может быть рабочим ; подобно кнопке равенства на электронном калькуляторе, он требует результата вычисления. Начиная с курсов алгебры, этот знак приобретает относительный смысл равенства между двумя вычислениями. Путаница между двумя способами использования знака иногда сохраняется на университетском уровне.
Равно
Знак равенства (=) в математике, в логике и других точных науках пишут между двумя идентичными по своему значению выражениями.
В античной и средневековой математике равенство обозначалось словесно (например est egale). Декарт в XVII веке вместо этого писал æ (от лат. aequalis ). Знак равенства в современной форме создал математик Роберт Рекорд (Robert Recorde, 1510—1558) в своём труде The Whetstone of Witte (1557). Он обосновал применение двух параллельных штрихов так (на староанглийском): «…bicause noe 2 thynges can be moare equalle», то есть «более равных вещей не бывает».
Символ Рекорда получил распространение далеко не сразу. Виет этим символом обозначал вычитание, а у Декарта он указывал, что коэффициент может быть отрицательным. В континентальной Европе знак «=» был введён Лейбницем на рубеже XVII—XVIII веков.
Математические знаки эквивалентности| знак | Unicode | значение | знак | Unicode | значение |
|---|---|---|---|---|---|
| = | U+003D | равно | ≠ | U+2260 | не равно |
| ≃ | U+2243 | ≄ | U+2244 | ||
| ≅ | U+2245 | ≆ | U+2246 | ||
| ≇ | U+2247 | ||||
| ≈ | U+2248 | ≉ | U+2249 | ||
| ≡ | U+2261 | идентично | ≢ | U+2262 | не идентично |
| ≌ | U+224C | ≂ | U+2242 | ||
| ≊ | U+224A | ≋ | U+224B | ||
| ≍ | U+224D | ≣ | U+2263 | ||
| ≎ | U+224E | ≏ | U+224F | ||
| ≐ | U+2250 | ≑ | U+2251 | ||
| ≒ | U+2252 | ≓ | U+2253 | ||
| ≔ | U+2254 | ≕ | U+2255 | ||
| ≘ | U+2258 | соответствует | ≚ | U+225A | |
| ≗ | U+2257 | ≙ | U+2259 | ||
| ≞ | U+225E | ≟ | U+225F | ||
| ≜ | U+225C | ≝ | U+225D | ||
| ≛ | U+225B | ≖ | U+2256 |
Похожие символы
— «приблизительно равно». Используется при обозначении двух величин, разницей между которыми в данной задаче можно пренебречь.
Применение в информатике
В языках программирования символ ‘=’ (в комбинации с другими, или же сам по себе) чаще всего используется для операций сравнения или присваивания, при сравнении также часто используются комбинации ‘>=’ (больше или равно) и ‘ >=’, ‘ Литература
Полезное
Смотреть что такое «Равно» в других словарях:
равно — сказ., употр. сравн. часто 1. В математике слово равно означает тождественность одной части выражения другой части. Три плюс три равно шесть. 2. Выражение всё равно означает снятие противоречия с предыдущими высказываниями, мыслями, окончательное … Толковый словарь Дмитриева
РАВНО — 1. Нареч. к равный в 1 знач., одинаково, так же (книжн.). «И хоть бесчувственному телу равно повсюду истлевать, но ближе к милому пределу мне все б хотелось почивать.» Пушкин. 2. в знач. сказуемого, чему. Равняется. Пять плюс три равно восьми. 3 … Толковый словарь Ушакова
РАВНО — 1. нареч. Одинаково, так же (книжн.). Р. красивы горы и леса. 2. в знач. сказ., чему. То же, что равняется (см. равняться в 4 знач.). Три плюс два р. пяти. • Равно как (равно как и, а равно и), союз (книжн.) как и, так же как и. Учебники, равно… … Толковый словарь Ожегова
равно — I. нареч. Одинаково, в равной мере, степени. * И хоть бесчувственному телу р. повсюду истлевать, но ближе к милому пределу мне всё б хотелось почивать (Пушкин). II. чему. в функц. сказ. Быть равным, одинаковым в каком л. отношении, равнозначным,… … Энциклопедический словарь
равно — См. и все равно. Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. равно равняется, в одинаковой степени, так же, в одинаковой мере, в равной степени, одинаково, эквивалентно, в равной… … Словарь синонимов
равно и — союз Употребляется при присоединении однородного члена предложения или части предложения, сопоставляемых с предыдущими как равнозначные, равноценные (иногда усиливая или отграничивая каждый из них от другого), соответствуя по значению сл.: как и … Современный толковый словарь русского языка Ефремовой
равно́ — равно, нареч. [не равно] … Русское словесное ударение
Равно. — равно. Начальная часть сложных слов, вносящая значение сл.: равный (равновесомый, равнобокий, равнокрылый и т.п.). Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
Равно — I нареч. качеств. количеств. В равной, в такой же мере или степени; одинаково. II предик. Будучи равным чему либо; равняется. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
Равно — I нареч. качеств. количеств. В равной, в такой же мере или степени; одинаково. II предик. Будучи равным чему либо; равняется. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
Равно — I нареч. качеств. количеств. В равной, в такой же мере или степени; одинаково. II предик. Будучи равным чему либо; равняется. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой