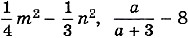При каких значениях переменной имеет смысл выражение что это значит
1. Рациональные выражения
В курсе алгебры 7 класса мы занимались преобразованиями целых выражений, т. е. выражений, составленных из чисел и переменных с помощью действий сложения, вычитания и умножения, а также деления на число, отличное от нуля. Так, целыми являются выражения
В отличие от них выражения
помимо действии сложения, вычитания и умножения, содержат деление на выражение с переменными. Такие выражения называют дробными выражениями.
Целые и дробные выражения называют рациональными выражениями.
Целое выражение имеет смысл при любых значениях входящих в него переменных, так как для нахождения значения целого выражения нужно выполнить действия, которые всегда возможны.
Дробное выражение при некоторых значениях переменных может не иметь смысла. Например, выражение 

Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.
Выражение вида 
Дробь, числитель и знаменатель которой многочлены, называют рациональной дробью.
Примерами рациональных дробей служат дроби
В рациональной дроби допустимыми являются те значения переменных, при которых не обращается в нуль знаменатель дроби.
Пример 1. Найдём допустимые значения переменной в дроби
Пример 2. При каком значении х значение дроби 
Упражнения


выпишите те, которые являются:
1. Рациональные выражения
В курсе алгебры 7 класса мы занимались преобразованиями целых выражений, т. е. выражений, составленных из чисел и переменных с помощью действий сложения, вычитания и умножения, а также деления на число, отличное от нуля. Так, целыми являются выражения
В отличие от них выражения
помимо действии сложения, вычитания и умножения, содержат деление на выражение с переменными. Такие выражения называют дробными выражениями.
Целые и дробные выражения называют рациональными выражениями.
Целое выражение имеет смысл при любых значениях входящих в него переменных, так как для нахождения значения целого выражения нужно выполнить действия, которые всегда возможны.
Дробное выражение при некоторых значениях переменных может не иметь смысла. Например, выражение 

Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.
Выражение вида 
Дробь, числитель и знаменатель которой многочлены, называют рациональной дробью.
Примерами рациональных дробей служат дроби
В рациональной дроби допустимыми являются те значения переменных, при которых не обращается в нуль знаменатель дроби.
Пример 1. Найдём допустимые значения переменной в дроби
Пример 2. При каком значении х значение дроби 
Упражнения


выпишите те, которые являются:
Область определения, выражение имеет смысл
Допустимые и недопустимые значения переменных
Данное определение связано с допустимыми значениями переменной. При введении определения посмотрим, к какому результату приведет.
Начиная с 7 класса, мы начинаем работать с числами и числовыми выражениями. Начальные определения с переменными переходят к значению выражений с выбранными переменными.
Когда имеются выражения с выбранными переменными, то некоторые из них могут не удовлетворять. Например, выражение вида 1:а, если а=, тогда оно не имеет смысла, так как делить на ноль нельзя. То есть выражение должно иметь такие значения, которые подойдут в любом случае и дадут ответ. Иначе говоря, имеют смысл с имеющимися переменными.
Если имеется выражение с переменными, то оно имеет смысл только тогда, когда при их подстановке значение может быть вычислено.
Если имеется выражение с переменными, то оно не имеет смысл, когда при их подстановке значение не может быть вычислено.
То есть отсюда следует полное определение
Существующими допустимыми переменными называют такие значения, при которых выражение имеет смысл. А если смысла не имеет, значит они считаются недопустимыми.
Для уточнения вышесказанного: если переменных более одной, тогда может быть и пара подходящих значений.
Для примера рассмотрим выражение вида 1x-y+z, где имеются три переменные. Иначе можно записать, как x=, y=1, z=2, другая же запись имеет вид (,1,2). Данные значения называют допустимыми, значит, можно найти значение выражения. Получим, что 1-1+2=11=1. Отсюда видим, что (1,1,2) недопустимы. Подстановка дает в результате деление на ноль, то есть 11-2+1=1.
Алгебраические выражения
Это то же самое числовое выражение, если в него добавить запретные буквы. Тогда оно и становится полноценным алгебраическим. Оно также может быть всех размеров и форм. Алгебраическое выражение – понятие более широкое, включающее в себя предыдущее. Но был смысл начинать разговор не с него, а с числового, чтобы было понятнее и разобраться было легче. Ведь имеет ли смысл выражение алгебраическое – вопрос не то чтобы очень сложный, но имеющий больше уточнений.
Условия для выражения, которое не имеет смысла
Когда задание начинается со слова «вычислить», можно говорить о преобразовании. Штука в том, что это действие не всегда целесообразно: в нем не то чтобы сильно нуждаются, если на передний план выходит выражение, не имеющее смысла. Примеры бесконечно удивительны: иногда, чтобы понять, что оно-то нас и настигло, приходится долго и нудно раскрывать скобки и считать-считать-считать…
Главное, что нужно запомнить: не имеет смысла то выражения, чей конечный результат сводится к запретному в математике действию. Если уж совсем по-честному, то тогда бессмысленным становится само преобразование, но для того, чтобы это выяснить, приходится его для начала выполнить. Такой вот парадокс!
Самое знаменитое, но от того не менее важное запретное математическое действие – это деление на ноль.
Потому вот, например, выражение, не имеющее смысла:
Если при помощи нехитрых вычислений свести вторую скобку к одной цифре, то она и будет нулем.
По такому же принципу «почетное звание» дается и этому выражению:
Типовые задачи по теме «Выражение, не имеющее смысла»
7 класс изучает эту тему по математике в числе прочих, и задания по ней встречаются нередко как непосредственно после соответствующего занятия, так и в качестве вопроса «с подвохом» на модулях и экзаменах.
Вот почему стоит рассмотреть типовые задачи и методы их решения.
Имеет ли смысл выражение:
Необходимо произвести все вычисление в скобках и привести выражение к виду:
Конечный результат содержит деление на ноль, следовательно, выражение не имеет смысла.
Какие выражения не имеют смысла?
Следует вычислить конечное значение для каждого из выражений.
Найти область допустимых значений для следующих выражений:
Область допустимых значений (ОДЗ) — это все те числа, при подставлении которых вместо переменных выражение будет иметь смысл.
То есть задание звучит как: найти значения, при которых не будет деления на ноль.
1) b є (-∞;-17) & (-17; + ∞), или b>-17 & b 25 & b 3 — x 2 y 3 + 13x — 38y)/(12x 2 — y).
Но на самом деле оно только выглядит страшным и громоздким, потому что на деле содержит в себе то, что уже давно известно: возведение чисел в квадрат и куб, некоторые арифметические действия, такие как деление, умножение, вычитание и сложения. Для удобства, между прочим, можно привести задачу к дробному виду.
Числитель у получившейся дроби не радует: (x 3 — x 2 y 3 + 13x — 38y). Это факт. Зато есть другой повод для счастья: его-то для решения задания трогать даже не понадобится! Согласно определению, рассмотренному ранее, делить нельзя на ноль, а что именно на него будет делиться, совершенно неважно. Потому оставляем это выражение в неизменном виде и подставляем пары чисел из данных вариантов в знаменатель. Уже третий пункт идеально вписывается, превращая небольшую скобочку в ноль. Но останавливаться на этом – плохая рекомендация, ведь подойти может еще что-нибудь. И вправду: пятый пункт тоже неплохо вписывается и подходит условию.