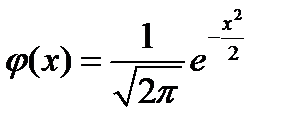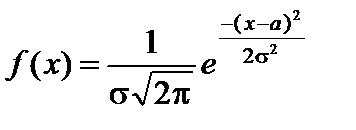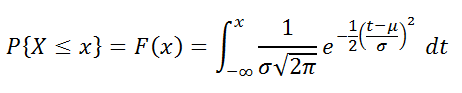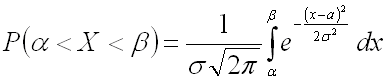При х 4 можно считать что функция гаусса равна
При х 4 можно считать что функция гаусса равна
В теории вероятностей и математической статистике занимают отдельное положение универсальные модели и методы, позволяющие изучать случайные явления. Ярким образцом данного утверждения служит функция Гаусса, разработанная немецким математиком астрономом, геодезистом и физиком К.-Ф. Гауссом (1777-1855).
Гауссова функция имеет вид: 
График функции y=ϕ(x) называют гауссовой кривой. Это «колоколообразная» кривая. Она имеет единственную точку максимума, симметрична относительно оси ординат, площадь под этой кривой равна единице. Она очень быстро асимптотически приближается к оси абсцисс:
Функция Гаусса является функцией плотности нормального распределения.
Кривая Гаусса по форме несколько напоминает колокол, поэтому график нормального закона часто еще называют колоколообразной кривой. Если вдруг увидите термин «колоколообразная кривая», знайте, что речь идет о нормальном распределении.
Как видно, у графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Другими словами, вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.
На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, т. е. вероятности попадания в обозначенные интервалы.
Функцию Гаусса также можно задать формулой: 
В функции плотности нормального распределения присутствует: две математические константы
π – соотношение длины окружности и его диаметра, равно примерно 3,142;
е – основание натурального логарифма, равно примерно 2,718;
два параметра, которые задают форму конкретной кривой
переменная x, для которой высчитывается значение функции, т.е. плотность вероятности.
Итак, конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии (σ 2 ). Кратко обозначается N(m, σ 2 ) или N(m, σ). Параметр m (математическое ожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ 2 характеризует размах вариации, то есть «размазанность» данных.
Плотность нормального распределения не имеет прямого практического применения (если не считать приближенных расчетов при использовании биномиального распределения).
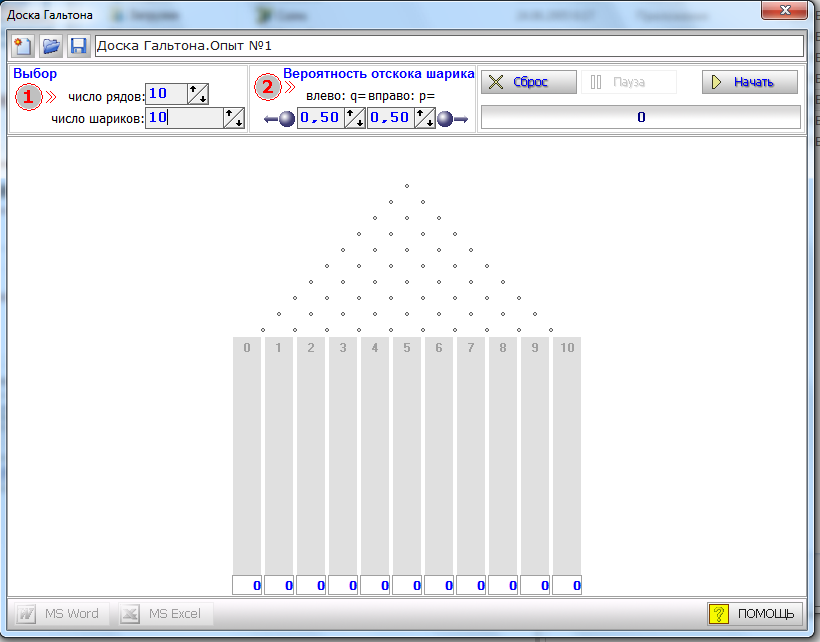
Для наглядной демонстрации действия гауссова закона распределения иногда используют специальное устройство — доску Гальтона (по имени её изобретателя). В нём сыплющиеся сверху одинаковые шарики распределяются по ходам между правильными шестиугольниками и в результате попадают на горизонтальную поверхность, образуя картинку, похожую на «подграфик» гауссовой кривой.
Посмотрите ролики, демонстрирующие принцип работы доски Гальтона:
Если ширина вертикальных столбцов гистограммы достаточно мала, а основания столбцов в объединении дают некоторый промежуток, то сама гистограмма похожа на график некоторой непрерывной функции, заданной на этом промежутке. Иногда такую функцию называют выравнивающей функцией.
Графики функций выравнивающих гистограммы похожи друг на друга. Все эти кривые распределения получаются из гауссовой кривой. Её часто называют кривой нормального распределения.
Задача 1. Используя модель доски Гальтона, подсчитайте:
1)чему равно число шаров, попавших в ячейки и ожидаемое число их попаданий, если а. шаров 100, а рядов 10; b. шаров 100, а рядов 29;
2) сколько было выпущено шаров, если математическое ожидание равно 18,87, дисперсия – 3,04, а число рядов 37;
3) какое среднее значение случайной величины Х и площадь гауссовой кривой, если 18 рядов, а количество шаров: а. 1343, b. 581?
Решение
Запускаем интерактивный модуль «Доска Гальтона», которая представленная на сайте «Вероятность в школе»
Задаём данное в условиях задачи число рядов и шаров и получаем наш результат для случая «А» и «Б» в котором искомые данные представлены в таблицах, экспортируемых как Word, так и Exsel.
Где указав значения параметров из условия, модель сама выполняет вычисление числа шаров в ячейках, строит столбчатую гистограмму
3. интерактивная модель представлена на Интернет-ресурсе Probability
Указав заданные значения ресурс производит автоматический подсчет запрашиваемых объектов
Нормальное распределение
Вероятность того, что случайная величина примет какое-либо значение из отрезка [α; β] равна:
Задача 2. Автомат изготавливает патроны. Случайная величина Х – «ошибка выпуска негодной продукции», которая распределена нормально со среднем квадратичным отклонением 0,4 мм и математическим ожиданием 0,6 мм. Постройте график функции плотности распределения величины Х. Оцените вероятность того, что ошибка появления бракованных патронов больше 0,1 мм, но меньше 0,76 мм. Какое значение не превышает модуль ошибки с вероятностью 0,89.
Решение
Применяемая таблица включает в свой состав ячейки для значений математического ожидания, стандартного отклонения, вероятности и интервала. Заполнив, которые мы мгновенно получаем искомую функцию, её график и требуемые задачей ответы
Нормальное распределение (Гаусса) в Excel
В статье подробно показано, что такое нормальный закон распределения случайной величины и как им пользоваться при решении практически задач.
Нормальное распределение в статистике
История закона насчитывает 300 лет. Первым открывателем стал Абрахам де Муавр, который придумал аппроксимацию биномиального распределения еще 1733 году. Через много лет Карл Фридрих Гаусс (1809 г.) и Пьер-Симон Лаплас (1812 г.) вывели математические функции.
Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение.
Нормальный закон не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. Конкретная форма распределения задается специальными параметрами. Например, у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами.
Кривая нормального распределения Гаусса имеет следующий вид.
График нормального распределения напоминает колокол, поэтому можно встретить название колоколообразная кривая. У графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.
На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.
Формула нормального распределения (плотности) следующая.
Формула состоит из двух математических констант:
е – основание натурального логарифма 2,718;
двух изменяемых параметров, которые задают форму конкретной кривой:
m – математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);
ну и сама переменная x, для которой высчитывается плотность вероятности.
Конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии ( σ 2 ). Кратко обозначается N(m, σ 2 ) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ 2 характеризует размах вариации, то есть «размазанность» данных.
Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности.
А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса концентрируется у центра. Если же у данных большой разброс, то они «размазываются» по широкому диапазону.
Плотность распределения не имеет прямого практического применения. Для расчета вероятностей нужно проинтегрировать функцию плотности.
Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:
Используя математические свойства любого непрерывного распределения, несложно рассчитать и любые другие вероятности, так как
P(a ≤ X 0 =1 и остается рассчитать только соотношение 1 на корень из 2 пи.
Таким образом, по графику хорошо видно, что значения, имеющие маленькие отклонения от средней, выпадают чаще других, а те, которые сильно отдалены от центра, встречаются значительно реже. Шкала оси абсцисс измеряется в стандартных отклонениях, что позволяет отвязаться от единиц измерения и получить универсальную структуру нормального распределения. Кривая Гаусса для нормированных данных отлично демонстрирует и другие свойства нормального распределения. Например, что оно является симметричным относительно оси ординат. В пределах ±1σ от средней арифметической сконцентрирована большая часть всех значений (прикидываем пока на глазок). В пределах ±2σ находятся большинство данных. В пределах ±3σ находятся почти все данные. Последнее свойство широко известно под названием правило трех сигм для нормального распределения.
Функция стандартного нормального распределения позволяет рассчитывать вероятности.
Понятное дело, вручную никто не считает. Все подсчитано и размещено в специальных таблицах, которые есть в конце любого учебника по статистике.
Таблица нормального распределения
Таблицы нормального распределения встречаются двух типов:
— таблица плотности;
— таблица функции (интеграла от плотности).
Таблица плотности используется редко. Тем не менее, посмотрим, как она выглядит. Допустим, нужно получить плотность для z = 1, т.е. плотность значения, отстоящего от матожидания на 1 сигму. Ниже показан кусок таблицы.
В зависимости от организации данных ищем нужное значение по названию столбца и строки. В нашем примере берем строку 1,0 и столбец 0, т.к. сотых долей нет. Искомое значение равно 0,2420 (0 перед 2420 опущен).
Функция Гаусса симметрична относительно оси ординат. Поэтому φ(z)= φ(-z), т.е. плотность для 1 тождественна плотности для -1, что отчетливо видно на рисунке.
Чтобы не тратить зря бумагу, таблицы печатают только для положительных значений.
На практике чаще используют значения функции стандартного нормального распределения, то есть вероятности для различных z.
В таких таблицах также содержатся только положительные значения. Поэтому для понимания и нахождения любых нужных вероятностей следует знать свойства стандартного нормального распределения.
Функция Ф(z) симметрична относительно своего значения 0,5 (а не оси ординат, как плотность). Отсюда справедливо равенство:
Это факт показан на картинке:
Значения функции Ф(-z) и Ф(z) делят график на 3 части. Причем верхняя и нижняя части равны (обозначены галочками). Для того, чтобы дополнить вероятность Ф(z) до 1, достаточно добавить недостающую величину Ф(-z). Получится равенство, указанное чуть выше.
Если нужно отыскать вероятность попадания в интервал (0; z), то есть вероятность отклонения от нуля в положительную сторону до некоторого количества стандартных отклонений, достаточно от значения функции стандартного нормального распределения отнять 0,5:
Для наглядности можно взглянуть на рисунок.
На кривой Гаусса, эта же ситуация выглядит как площадь от центра вправо до z.
Довольно часто аналитика интересует вероятность отклонения в обе стороны от нуля. А так как функция симметрична относительно центра, предыдущую формулу нужно умножить на 2:
Под кривой Гаусса это центральная часть, ограниченная выбранным значением –z слева и z справа.
Указанные свойства следует принять во внимание, т.к. табличные значения редко соответствуют интересующему интервалу.
Для облегчения задачи в учебниках обычно публикуют таблицы для функции вида:
Если нужна вероятность отклонения в обе стороны от нуля, то, как мы только что убедились, табличное значение для данной функции просто умножается на 2.
Теперь посмотрим на конкретные примеры. Ниже показана таблица стандартного нормального распределения. Найдем табличные значения для трех z: 1,64, 1,96 и 3.
Как понять смысл этих чисел? Начнем с z=1,64, для которого табличное значение составляет 0,4495. Проще всего пояснить смысл на рисунке.
То есть вероятность того, что стандартизованная нормально распределенная случайная величина попадет в интервал от 0 до 1,64, равна 0,4495. При решении задач обычно нужно рассчитать вероятность отклонения в обе стороны, поэтому умножим величину 0,4495 на 2 и получим примерно 0,9. Занимаемая площадь под кривой Гаусса показана ниже.
Таким образом, 90% всех нормально распределенных значений попадает в интервал ±1,64σ от средней арифметической. Я не случайно выбрал значение z=1,64, т.к. окрестность вокруг средней арифметической, занимающая 90% всей площади, иногда используется для проверки статистических гипотез и расчета доверительных интервалов. Если проверяемое значение не попадает в обозначенную область, то его наступление маловероятно (всего 10%).
Для проверки гипотез, однако, чаще используется интервал, накрывающий 95% всех значений. Половина вероятности от 0,95 – это 0,4750 (см. второе выделенное в таблице значение).
Для этой вероятности z=1,96. Т.е. в пределах почти ±2σ от средней находится 95% значений. Только 5% выпадают за эти пределы.
Еще одно интересное и часто используемое табличное значение соответствует z=3, оно равно по нашей таблице 0,4986. Умножим на 2 и получим 0,997. Значит, в рамках ±3σ от средней арифметической заключены почти все значения.
Так выглядит правило 3 сигм для нормального распределения на диаграмме.
С помощью статистических таблиц можно получить любую вероятность. Однако этот метод очень медленный, неудобный и сильно устарел. Сегодня все делается на компьютере. Далее переходим к практике расчетов в Excel.
Нормальное распределение в Excel
В Excel есть несколько функций для подсчета вероятностей или обратных значений нормального распределения.
Функция НОРМ.СТ.РАСП
Функция НОРМ.СТ.РАСП предназначена для расчета плотности ϕ( z ) или вероятности Φ(z) по нормированным данным (z).
z – значение стандартизованной переменной
интегральная – если 0, то рассчитывается плотность ϕ( z ) , если 1 – значение функции Ф(z), т.е. вероятность P(Z
Русские Блоги
Детальный анализ гауссовой функции
резюме
Важным элементом, встречающимся в статье, является функция ядра Гаусса, но необходимо проанализировать различные потенциальные свойства функции Гаусса.В этой статье сначала упоминаются соответствующие материалы, чтобы дать основу для функции ядра Гаусса, а затем используется matlab для автоматического сохранения гауссиана при различных параметрах. GIF-анимация изменения функции ядра и исходный код передаются одновременно, что также удобно для последующей записи на бумаге.
Основа гауссовской функции
2.1 Одномерная гауссовская функция
Гауссова функция, функция Гаусса, также для краткости называемая гауссовой, имеет одномерную форму следующим образом:
Гауссовы функции широко используются в области статистики для выражения нормального распределения. В области обработки сигналов они используются для определения гауссовых фильтров. В области обработки изображений в Gaussian Blur часто используются двумерные функции ядра Гаусса. Он используется для решения тепловых уравнений и уравнений диффузии, а также для определения преобразования Вейерштрасса.
Из приведенного выше рисунка видно, что функция Гаусса является экспоненциальной функцией, а ее лог-функция представляет собой логарифмическую вогнутую квадратичную функцию, логарифм которой является вогнутой квадратичной функцией.
Интеграл от функции Гаусса является функцией ошибки, однако ее аномальный интеграл по всей сплошной линии может быть точно вычислен с использованием следующего гауссова интеграла
Интеграл приведенной выше формулы равен 1, в этом случае Гаусс является функцией плотности вероятности нормально распределенной случайной величины, ожидаемое значение μ = b, дельта дисперсии ^ 2 = c ^ 2, то есть
2.2 Двумерная функция Гаусса
Двумерная функция Гаусса, как
2.3 Анализ функции Гаусса
В этом разделе Matlab используется для интуитивного просмотра функции Гаусса. В реальных приложениях программирования параметры в функции Гаусса
ksize размер гауссовской функции
сигма-дисперсия гауссовской функции
функция центральная гауссова функция центральная координата
смещение Смещение пиковой центральной точки функции Гаусса, используемой для управления усеченной функцией Гаусса
Чтобы упростить интуитивное наблюдение за изменениями параметров функции Гаусса и отличающимися результатами, в следующем коде реализован автоматический прирост параметров и сохранены все карты результатов в виде изображений gif, сначала вставьте полный код:
С увеличением сигмы пик всей функции Гаусса постепенно уменьшается, и все становится более сглаженным, эффект сглаживания на изображении становится все более очевидным.
Оставьте параметры без изменений, урежьте указанную выше гауссовскую функцию, то есть урезанную гауссовскую функцию, размер смещения равен ksize * 3/10, тогда результат будет следующим:
Функция усеченной гауссовской функции в основном состоит в том, чтобы больше не учитывать исходную информацию изображения в определенной области, что обеспечивает более разумное использование окружающих пикселей вблизи центральной точки гауссовой функции, а также можно изменять координаты центра гауссовой функции, как показано ниже:
Чтобы облегчить наблюдение за эффектом усечения, угол обзора был изменен.
Гауссова свёртка функции ядра
В статье для свертки используются гауссовская карта и карта пространственных объектов. Исходя из текущих результатов, необходимо изменить параметры обрезки гауссовой функции с расстоянием до границы, поскольку, если исходная гауссовская функция используется для края изображения, она появится на границе. Причина нижнего круга также очень проста: когда гауссова функция представляет собой гауссову свертку с исходным изображением, край изображения вычисляется как 0, так как решить проблему с краем?
Сначала посмотрите на кусок кода:
И сверните следующую цифру 7,
Сначала ядром свертки является исходная неусеченная функция ядра Гаусса, затем результат показан на рисунке 8.
Можно видеть, что результат свертки на краю изображения выглядит непредсказуемым, а значение на краю значительно уменьшается, что является результатом того, что функция ядра Гаусса вычисляет деталь вне изображения как 0 на краю. Функции ядра Гаусса должны быть предназначены для усечения, но предпосылка состоит в том, чтобы освоить закон смещения, который будет подробно проанализирован ниже.
Если вы используете функцию ядра Гаусса из рисунка 6 и рисунка 7 для операции свертки, как показано на рисунке 9:
Можно видеть, что по сравнению с фиг.8 часть, соответствующая функции ядра Гаусса, изменилась, то есть:
При приближении к краю измените значение i или j, чтобы обеспечить плавную обработку по краю. Но изменение функции ядра Гаусса таким образом, использование Matlab не является хорошим решением этой проблемы, или использование края изображения, которое нужно обработать, чтобы расширить размер смещения, свертывание со стандартной функцией ядра Гаусса, а затем отрезание части, которая превышает исходное изображение. В настоящее время наиболее подходящий и простой способ обработки для операции свертки с использованием функции imfilter в Matlab описан здесь в первую очередь, эта часть не является основной частью статьи, а является лишь умелым методом программирования числовой операции.