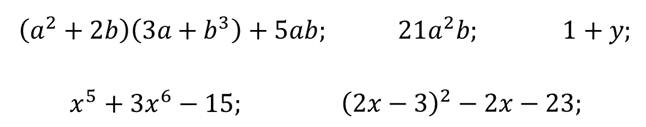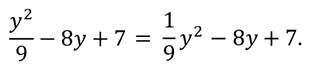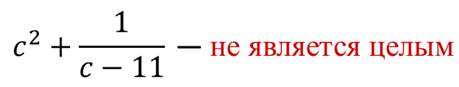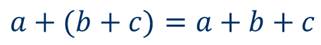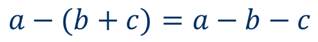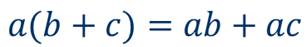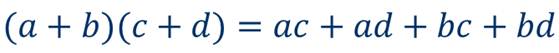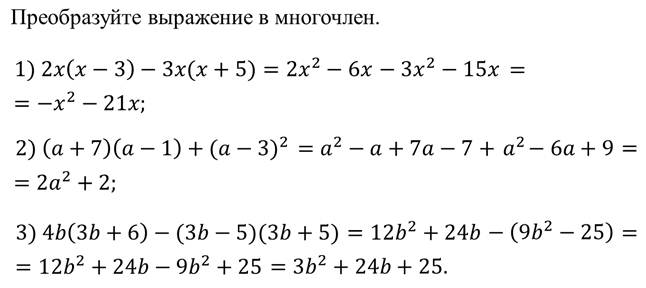Преобразовать в многочлен это что значит
Что значит преобразовать в многочлен выражение?
А значит, и любое целое выражение, мы можем представить в виде многочлена. Для этого достаточно в целом выражении раскрыть скобки и привести подобные слагаемые. В результате необходимо получиться выражение, которое представляет собой алгебраическую сумму нескольких одночленов.
Что значит преобразовать в многочлен стандартного вида?
Итак, привести многочлен к стандартному виду – это значит заменить исходный многочлен тождественно равным ему многочленом стандартного вида, полученным из исходного путем проведения тождественных преобразований.
Можно ли любое целое выражение преобразовать в многочлен стандартного вида?
е. чтобы найти произведение многочленов, необходимо каждый член одного многочлена умножить на каждый член другого многочлена, а полученные одночлены сложить. … Любое целое выражение можно преобразовать в многочлен стандартного вида.
Как преобразовать произведение многочленов в многочлен стандартного вида?
Обычно пользуются другой формулировкой. Чтобы умножить многочлен на многочлен, достаточно каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить. Преобразуем произведения многочленов 5х3 + 2х – 3 – х2 и 2 + 4х2 – х в многочлен стандартного вида.
Что значит представить в виде произведения многочленов?
Разложить многочлен на множители — это значит представить многочлен в виде произведения двух или нескольких множителей.
Как преобразовывать выражение в одночлен стандартного вида?
Чтобы привести одночлен к стандартному виду нужно сделать следующее.
Как возводить в многочлен?
Чтобы возвести многочлен в степень n, нужно последовательно умножать этот многочлен сам на себя n раз. При умножении многочлена на многочлен применяются свойства многочленов. Также существуют формулы сокращенного умножения, которые помогают возводить многочлены в степени, избегая последовательного перемножения.
Какое из выражений не является целым?
Если же в выражении присутствует деление на переменную или на другое выражение содержащее переменную, то такое выражение не является целым. Такое выражение называется дробным.
Что значит упростить выражение 7 класс?
Упростить выражение – это значит уменьшить количество операций, которые необходимо сделать, чтобы вычислить его значение при конкретных значениях переменных.
Что такое целые выражения примеры?
Определение и примеры целых выражений
Что значит выражение является рациональным?
Рациональное выражение – это любое выражение, составленное из чисел, буквенных переменных, арифметических операций и возведения в степень.
Что называется алгебраическим выражением и переменной?
Алгебраическим выражением — имеющее смысл выражение, составленное из букв, знаков арифметических действий, чисел и скобок. a 2 − 3 b — алгебраическое выражение. Буквы, которые являются составной частью алгебраического выражения, могут принимать разные числовые значения. Поэтому, они (буквы) называются переменными.
Как представить выражение в виде многочлена стандартного вида?
Чтобы привести многочлен к стандартному виду, нужно: 1) Каждый член многочлена представить в стандартном виде; 2) Привести подобные члены многочлена.
Как определить степень многочлена стандартного вида?
Итак, чтобы найти степень многочлена:
Преобразование целого выражения в многочлен
Урок 37. Алгебра 7 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Преобразование целого выражения в многочлен»
· ввести понятие «целое выражение»;
· показать, что любое целое выражение можно представить в виде многочлена;
· показать способ определения целого выражения;
· показать способ преобразования целого выражения в многочлен стандартного вида.
В первую очередь необходимо выяснить, какие же выражения называют целыми.
Посмотрите внимательно на следующие выражения
Они составлены из чисел и переменных с помощью действий сложения, вычитания и умножения. Также некоторые из выражений содержат степени.
Такие выражения называют целыми. Причём если выражение содержит, кроме действий сложения, вычитания и умножения, действие деление на число, не равное нулю, то оно также является целым, так как действие деление можно заменить умножением на число обратное делителю.
Следующее же выражение не является целым, так содержит деление на выражение с переменной.
Обратите внимание, что среди целых выражений есть многочлены и одночлены.
Нам с вами известно, что сумму, разность и произведение многочленов можно преобразовать в многочлен. Поэтому любое целое выражение можно представить в виде многочлена.
Прежде, чем рассмотреть примеры преобразования целого выражения в многочлен, вспомним, что если перед скобками стоит знак плюс, то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки.
Если же перед скобками стоит знак минус, то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки, на противоположный.
Также вспомним, что при умножении одночлена на многочлен надо умножить одночлен на каждый член многочлена.
А при умножении многочлена на многочлен надо каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить.
Ну а теперь давайте рассмотрим примеры.
Итак, чтобы преобразовать целое выражение в многочлен, надо:
1. раскрыть скобки, если они есть;
2. применить формулы сокращённого умножения, если возможно;
3. при необходимости привести подобные слагаемые, чтобы получить многочлен стандартного вида.
Помним, что многочленом стандартного вида называется многочлен, все члены которого имеют стандартный вид и среди них нет подобных.
Многочлен стандартного вида
Определение многочлена
Многочлен — это сумма одночленов. Получается, что многочлен — не что иное, как несколько одночленов, собранных «под одной крышей».
Одночлен — это частный случай многочлена.
Рассмотрим примеры многочленов:
Если многочлен состоит из двух одночленов, его называют двучленом:
Многочлен — это сумма одночленов, поэтому знак «минус» относится к числовому коэффициенту одночлена. Именно поэтому мы записываем – 3×2, а не просто 3×2.
Этот же многочлен можно записать вот так:
Это значит, что каждый одночлен важно рассматривать вместе со знаком, который перед ним стоит.
Многочлен вида 10x – 3×2 + 7 называется трехчленом.
Линейный двучлен — это многочлен первой степени: ax + b. a и b здесь — некоторые числа, x — переменная.
Если разделить многочлен с переменной x на линейный двучлен x – b (где b — некоторое положительное или отрицательное число) — остаток будет только многочленом нулевой степени. То есть некоторым числом N, которое можно определить без поиска частного.
Если многочлен содержит обычное число — это число является свободным членом многочлена.
Свободный член многочлена не имеет буквенной части. Кроме того, любое числовое выражение — это многочлен. Например, вот такие числовые выражения — тоже многочлены:
Такие выражения состоят из свободных членов.
Многочлен стандартного вида
Недостаточно просто знать, что такое многочлен и что такое одночлен. Это целая алгебраическая экосистема, где у всего есть названия, определения и особенности.
Давайте разберемся, что такое многочлен стандартного вида. Многочленом стандартного вида называют многочлен, каждый член которого имеет одночлен стандартного вида и не содержит подобных членов.
Получается, что всякий многочлен можно привести к стандартному виду. Таким образом можно получить многочлен, работать с которым гораздо проще и приятнее.
К стандартному виду многочлен приводится очень просто. Нужно лишь привести в нем подобные слагаемые.
Подобные слагаемые — это подобные члены многочлена. Приведение подобных слагаемых в многочлене — приведение его подобных членов. Тут же возникает резонный вопрос: Что такое подобные члены многочлена? Это члены с одинаковой буквенной частью.
Давайте разберем на примере, как «нестандартный» многочлен приводится к стандартному виду.
Дан красавец многочлен: 3x + 5xy2 + x – xy2
Приведем подобные слагаемые. Для этого найдем все члены с одинаковыми буквенными составляющими:
Как видите, в получившемся многочлене нет подобных членов. Такой многочлен — это многочлен стандартного вида.
Степень многочлена
Многочлен может иметь степень — имеет на это полное право.
Степень многочлена стандартного вида — это наибольшая из степеней, входящих в него одночленов.
Из определения можно сделать вывод, что степень многочлена возможно определить только после приведения его к стандартному виду.
Рассмотрим на примере:
Дан многочлен 6x + 4xy2 + x + xy2
Сначала приводим многочлен к стандартному виду — для этого приводим подобные слагаемые:
Получаем многочлен стандартного вида 6x + 4xy2 + x + xy2 = 7x + 5xy2.
Отсюда делаем вывод, что многочлен 7x + 5xy2 — многочлен второй степени.
Кроме того, можно сделать вывод, что и исходный многочлен 6x + 4xy2 + x + xy2 — многочлен второй степени, поскольку оба многочлена равны друг другу.
В некоторых случаях необходимо сначала привести к стандартному виду одночлены многочлена, а затем уже и сам многочлен.
Пример:
Получившийся многочлен без труда приводим к стандартному виду. Приводим подобные слагаемые:
Коэффициенты многочлена
Коэффициенты членов многочлена — это числа, которые указаны перед переменными множителями. Если перед переменной нет числа, то коэффициент этого члена = 1.
Иными словами — коэффициенты членов многочлена — это члены многочлена, представленные в виде стандартных одночленов.
Например:
Все одночлены имеют стандартный вид. 2, 5 и 18 — коэффициенты членов данного многочлена.
Кажется, со стандартным видом многочлена все понятно. Чтобы без труда приводить любой многочлен к стандартному виду, нужно потренироваться, ведь в 7 классе только и разговоров, что о многочленах. Давайте разберем несколько примеров. Попробуйте решить их самостоятельно, сверяясь с ответами.
Задание раз. Приведите многочлен к стандартному виду и определите его степень: 4x + 6xy2 + x – xy2.
Как решаем: приведем подобные слагаемые. Для этого найдем все члены с одинаковыми буквенными составляющими:
Получаем многочлен стандартного вида: 4x + 6xy2 + x – xy2 = 5x + 5xy2.
Ответ: стандартный вид многочлена 5x + 5xy2. Данный многочлен — многочлен второй степени.
Многочлен приведен к стандартному виду.
Как решаем: приведем подобные слагаемые. Для этого найдем все члены с одинаковыми буквенными составляющими:
Разобраться в многочленах не так-то просто. В этой теме немало нюансов и подводных камней. Чтобы не запутаться в множестве похожих одно на другое определений, побольше практикуйтесь. Чтобы перейти на следующую ступень и начать выполнение арифметических действий с многочленами, важно научиться приводить многочлен к стандартному виду.
Преобразование целых выражений
Благодаря курсу алгебры, известно, что все выражения требуют преобразования для более удобного решения. Определение целых выражений способствует тому, что для начала выполняются тождественные преобразования. Будем преобразовывать выражение в многочлен. В заключении разберем несколько примеров.
Определение и примеры целых выражений
Целые выражения – это числа, переменные или выражения со сложением или вычитанием, которые записываются в виде степени с натуральным показателем, которые также имеют скобки или деление, отличное от нуля.
Многочлен и одночлен являются целыми выражениями, с которыми встречаемся в школе при работе с рациональными числами. Иначе говоря, целые выражения не включают в себя записи иррациональных дробей. Другое название – это целые иррациональные выражения.
Какие преобразования целых выражений возможны?
Целые выражения рассматриваются при решении как основные тождественные преобразования, раскрытие скобок, группирование, приведение подобных.
Для начала необходимо применить правило раскрытия скобок. Получим выражение вида 2 · ( a 3 + 3 · a · b − 2 · a ) − 2 · a 3 − ( 5 · a · b − 6 · a + b ) = = 2 · a 3 + 2 · 3 · a · b + 2 · ( − 2 · a ) − 2 · a 3 − 5 · a · b + 6 · a − b = = 2 · a 3 + 6 · a · b − 4 · a − 2 · a 3 − 5 · a · b + 6 · a − b
После чего можем привести подобные слагаемые:
Представить выражение 6 · x 2 · y + 18 · x · y − 6 · y − ( x 2 + 3 · x − 1 ) · ( x 3 + 4 · x ) в виде произведения.
6 · y · ( x 2 + 3 · x − 1 ) − ( x 2 + 3 · x − 1 ) · ( x 3 + 4 · x ) = = ( x 2 + 3 · x − 1 ) · ( 6 · y − ( x 3 + 4 · x ) )
Ответ: 6 · x 2 · y + 18 · x · y − 6 · y − ( x 2 + 3 · x − 1 ) · ( x 3 + 4 · x ) = = ( x 2 + 3 · x − 1 ) · ( 6 · y − x 3 − 4 · x )
Тождественные преобразования требуют строгое выполнение порядка действий.
8 · x 8 + 4 · x : 8 = 8 · x 8 + 4 · x · 1 8 = 8 · x 8 + 4 · 1 8 · x = 8 · x 8 + 1 2 · x
Преобразование в многочлен
Большинство случаев преобразования целых выражений – это представление в виде многочлена. Любое выражение можно представить в виде многочлена. Любое выражение может быть рассмотрено как многочлены, соединенные арифметическими знаками. Любое действие над многочленами в итоге дает многочлен.
Для того, чтобы выражение было представлено в виде многочлена, необходимо выполнять все действия с многочленами, согласно алгоритму.
Разберем умножение. Видно, что 2 · ( 2 · x 3 − 1 ) = 4 · x 3 − 2 и ( 4 · x 2 − 4 · x + 1 ) · ( 3 − x ) = 12 · x 2 − 4 · x 3 − 12 · x + 4 · x 2 + 3 − x = = 16 · x 2 − 4 · x 3 − 13 · x + 3
Выполняем сложение, после чего придем к выражению:
Умножение и возведение в степень многочлена говорит о том, что необходимо использовать формулы сокращенного умножения для ускорения процесса преобразования. Это способствует тому, что действия будут выполнены рационально и правильно.
Чтобы преобразование не было слишком длинным, необходимо заданное выражение приводить к стандартному виду.
Упростить выражение вида ( 2 · a · ( − 3 ) · a 2 · b ) · ( 2 · a + 5 · b 2 ) + a · b · ( a 2 + 1 + a 2 ) · ( 6 · a + 15 · b 2 ) + ( 5 · a · b · ( − 3 ) · b 2 )
− 6 · a 3 · b · ( 2 · a + 5 · b 2 ) + a · b · ( 2 · a 2 + 1 ) · ( 6 · a + 15 · b 2 ) − 15 · a · b 3 = = − 12 · a 4 · b − 30 · a 3 · b 3 + ( 2 · a 3 · b + a · b ) · ( 6 · a + 15 · b 2 ) − 15 · a · b 3 = = − 12 · a 4 · b − 30 · a 3 · b 3 + 12 · a 4 · b + 30 · a 3 · b 3 + 6 · a 2 · b + 15 · a · b 3 − 15 · a · b 3 = = ( − 12 · a 4 · b + 12 · a 4 · b ) + ( − 30 · a 3 · b 3 + 30 · a 3 · b 3 ) + 6 · a 2 · b + ( 15 · a · b 3 − 15 · a · b 3 ) = 6 · a 2 · b
Ответ: ( 2 · a · ( − 3 ) · a 2 · b ) · ( 2 · a + 5 · b 2 ) + a · b · ( a 2 + 1 + a 2 ) · ( 6 · a + 15 · b 2 ) + + ( 5 · a · b · ( − 3 ) · b 2 ) = 6 · a 2 · b
Преобразование целых выражений.
Данная статья посвящена одному из видов выражений курса алгебры – целым выражениям, а также их преобразованию. Сначала дадим определение целых выражений. Дальше покажем, какие тождественные преобразования наиболее часто выполняются с ними. Наконец, покажем, что любое целое выражение можно преобразовать в многочлен, и на примерах разберем, как это преобразование проводится и на чем оно основано.
Навигация по странице.
Определение и примеры целых выражений
Изучение целых выражений входит в программу курса алгебры для 7 классов. На уроках алгебры и дается следующее определение целых выражений.
Целыми выражениями называют числа, переменные, а также всевозможные выражения, составленные из них при помощи действий сложения, вычитания и умножения (произведение одинаковых множителей может быть записано и в виде степени с натуральным показателем), которые также могут содержать скобки и деление на отличное от нуля число.
К слову, любой многочлен, как и любой одночлен, являются целыми выражениями.
Следует отметить, что в школе мы работаем преимущественно с такими целыми выражениями, которые если содержат в своей записи числа, то эти числа рациональные (в частности, целые или натуральные). Иными словами, изучаемые в школе целые выражения не содержат в своей записи иррациональных чисел. Их еще называют целыми рациональными выражениями.
Какие преобразования целых выражений возможны?
С целыми выражениями можно выполнять все основные тождественные преобразования, такие как раскрытие скобок, группировка слагаемых и множителей, приведение подобных слагаемых и т.п. Рассмотрим решения нескольких примеров.
Преобразуйте целое выражение 

Представьте целое выражение 6·x 2 ·y+18·x·y−6·y−(x 2 +3·x−1)·(x 3 +4·x) в виде произведения двух многочленов.
Напомним, что при выполнении тождественных преобразований выражений, в том числе и целых, нужно соблюдать порядок выполнения действий.
Преобразование в многочлен
Во многих случаях преобразования целых выражений проводятся с единственной целью – представить их в виде многочленов. Вообще, любое целое выражение можно представить в виде многочлена. Это утверждение следует из определения целого выражения, которое мы дали выше, а также из того, как мы определены действия с многочленами и одночленами. Действительно, всякое целое выражение мы можем рассматривать как соединенные знаками действий многочлены, а мы знаем, что умножение многочленов, как и их сложение и вычитание в результате дает многочлен.
Чтобы целое выражение представить в виде многочлена, надо выполнить все действия с многочленами, одночленами и числами, составляющими это выражение, согласно принятому порядку выполнения действий.
Исходное целое выражение содержит и скобки, и возведение в степень, и действия разных ступеней.
Понятно, что при выполнении умножения многочленов и возведении их в степень по возможности следует пользоваться формулами сокращенного умножения, что ускорит процесс преобразования. Например, в предыдущем примере возведение многочлена 2·x−1 в квадрат было целесообразно проводить с использованием формулы квадрата разности. Да и вообще, любые действия желательно выполнять максимально рационально.
В заключение этой статьи отметим, что процесс преобразования в многочлен будет намного короче, если предварительно все составляющие исходное целое выражение одночлены и многочлены привести к стандартному виду.