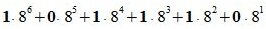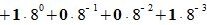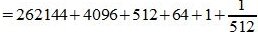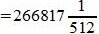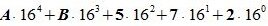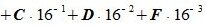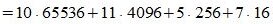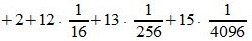представить десятичное число 50 в двоичном коде
Перевести число 50 из десятичной системы в двоичную
Задача: перевести число 50 из десятичной системы счисления в двоичную
Для того, чтобы перевести число 50 из десятичной системы счисления в двоичную, необходимо осуществить последовательное деление на 2, то тех пор пока остаток не будет меньше чем 2.
| — | 50 | 2 | ||
| 50 | — | 25 | 2 | |
| 0 | 24 | — | 12 | 2 |
| 1 | 12 | — | 6 | 2 |
| 0 | 6 | — | 3 | 2 |
| 0 | 2 | 1 | ||
| 1 |
Полученные остатки записываем в обратном порядке, таким образом:
Подробнее о том, как переводить числа из десятичной системы в двоичную, смотрите здесь.
Перевод чисел из одной системы счисления в другую
Данный конвертер переводит числа между наиболее популярными системами счисления: десятичной, двоичной, восьмеричной, шестнадцатеричной.
Существуют и другие системы счисления, но мы не стали включать их в конвертер из-за низкой популярности.
Для указания системы счисления при записи числа используется нижний индекс, который ставится после числа:
20010 = 110010002 = 3108 = C816
Кратко об основных системах счисления
Десятичная система счисления. Используется в повседневной жизни и является самой распространенной. Все числа, которые нас окружают представлены в этой системе. В каждом разряде такого числа может использоваться только одна цифра от 0 до 9.
Двоичная система счисления. Используется в вычислительной технике. Для записи числа используются цифры 0 и 1.
Восьмеричная система счисления. Также иногда применяется в цифровой технике. Для записи числа используются цифры от 0 до 7.
Перевод в десятичную систему счисления
Перевод из десятичной системы счисления в другие
Делим десятичное число на основание системы, в которую хотим перевести и записываем остатки от деления. Запишем полученные остатки в обратном порядке и получим искомое число.
Переведем число 37510 в восьмеричную систему:
Перевод из двоичной системы в восьмеричную
Так же как и в первом способе разбиваем число на группы. Но вместо преобразований в скобках просто заменим полученные группы (триады) на соответствующие цифры восьмеричной системы, используя таблицу триад:
Перевод из двоичной системы в шестнадцатеричную
Также как и в первом способе разбиваем число на группы по 4 цифры. Заменим полученные группы (тетрады) на соответствующие цифры шестнадцатеричной системы, используя таблицу тетрад:
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Перевод из восьмеричной системы в двоичную
Каждый разряд восьмеричного числа будем делить на 2 и записывать остатки в обратном порядке, формируя группы по 3 разряда двоичного числа. Если в группе получилось меньше 3 разрядов, тогда дополняем нулями. Записываем все группы по порядку, отбрасываем ведущие нули, если имеются, и получаем двоичное число.
Используем таблицу триад:
Каждую цифру исходного восьмеричного числа заменяется на соответствующие триады. Ведущие нули самой первой триады отбрасываются.
Перевод из шестнадцатеричной системы в двоичную
Аналогично переводу из восьмеричной в двоичную, только группы по 4 разряда.
Используем таблицу тетрад:
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Каждую цифру исходного числа заменяется на соответствующие тетрады. Ведущие нули самой первой тетрады отбрасываются.
Перевод из восьмеричной системы в шестнадцатеричную и наоборот
Такую конвертацию можно осуществить через промежуточное десятичное или двоичное число. То есть исходное число сначала перевести в десятичное (или двоичное), и затем полученный результат перевести в конечную систему счисления.
Перевод чисел из одной системы счисления в другую онлайн
С помощю этого онлайн калькулятора можно перевести целые и дробные числа из одной системы счисления в другую. Дается подробное решение с пояснениями. Для перевода введите исходное число, задайте основание сисемы счисления исходного числа, задайте основание системы счисления, в которую нужно перевести число и нажмите на кнопку «Перевести». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Перевод целых и дробных чисел из одной системы счисления в любую другую − теория, примеры и решения
Существуют позиционные и не позиционные системы счисления. Арабская система счисления, которым мы пользуемся в повседневной жизни, является позиционной, а римская − нет. В позиционных системах счисления позиция числа однозначно определяет величину числа. Рассмотрим это на примере числа 6372 в десятичном системе счисления. Пронумеруем это число справа налево начиная с нуля:
| число | 6 | 3 | 7 | 2 |
| позиция | 3 | 2 | 1 | 0 |
Тогда число 6372 можно представить в следующем виде:
Число 10 определяет систему счисления (в данном случае это 10). В качестве степеней взяты значения позиции данного числа.
Рассмотрим вещественное десятичное число 1287.923. Пронумеруем его начиная с нуля позиции числа от десятичной точки влево и вправо:
| число | 1 | 2 | 8 | 7 | . | 9 | 2 | 3 |
| позиция | 3 | 2 | 1 | 0 | -1 | -2 | -3 |
Тогда число 1287.923 можно представить в виде:
В общем случае формулу можно представить в следующем виде:
В таблице Таб.1 представлены числа в разных системах счисления.
| Таблица 1 | |||
|---|---|---|---|
| Система счисления | |||
| 10 | 2 | 8 | 16 |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
Перевод чисел из одной системы счисления в другую
Для перевода чисел с одной системы счисления в другую, проще всего сначала перевести число в десятичную систему счисления, а затем, из десятичной системы счисления перевести в требуемую систему счисления.
Перевод чисел из любой системы счисления в десятичную систему счисления
С помощью формулы (1) можно перевести числа из любой системы счисления в десятичную систему счисления.
Пример 1. Переводить число 1011101.001 из двоичной системы счисления (СС) в десятичную СС. Решение:
Пример 2. Переводить число 1011101.001 из восьмеричной системы счисления (СС) в десятичную СС. Решение:
Пример 3. Переводить число AB572.CDF из шестнадцатеричной системы счисления в десятичную СС. Решение:
Перевод чисел из десятичной системы счисления в другую систему счисления
Для перевода чисел из десятичной системы счисления в другую систему счисления нужно переводить отдельно целую часть числа и дробную часть числа.
Пример 4. Переведем число 159 из десятичной СС в двоичную СС:
| 159 | 2 | ||
| 158 | 79 | 2 | |
| 1 | 78 | 39 | 2 |
| 1 | 38 | 19 | 2 |
| 1 | 18 | 9 | 2 |
| 1 | 8 | 4 | 2 |
| 1 | 4 | 2 | 2 |
| 0 | 2 | 1 | |
| 0 |
Как видно из Рис. 1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111. Следовательно можно записать:
Пример 5. Переведем число 615 из десятичной СС в восьмеричную СС.
| 615 | 8 | ||
| 608 | 76 | 8 | |
| 7 | 72 | 9 | 8 |
| 4 | 8 | 1 | |
| 1 |
При приведении числа из десятичной СС в восьмеричную СС, нужно последовательно делить число на 8, пока не получится целый остаток меньшее, чем 8. В результате построив число из остатков деления (справа налево) получим число в восьмеричной СС: 1147(см. Рис. 2). Следовательно можно записать:
Пример 6. Переведем число 19673 из десятичной системы счисления в шестнадцатеричную СС.
| 19673 | 16 | ||
| 19664 | 1229 | 16 | |
| 9 | 1216 | 76 | 16 |
| 13 | 64 | 4 | |
| 12 |
Далее рассмотрим перевод правильных десятичных дробей в двоичную СС, в восьмеричную СС, в шестнадцатеричную СС и т.д.
Для перевода правильных десятичных дробей (вещественное число с нулевой целой частью) в систему счисления с основанием s необходимо данное число последовательно умножить на s до тех пор, пока в дробной части не получится чистый нуль, или же не получим требуемое количество разрядов. Если при умножении получится число с целой частью, отличное от нуля, то эту целую часть не учитывать (они последовательно зачисливаются в результат).
Рассмотрим вышеизложенное на примерах.
Пример 7. Переведем число 0.214 из десятичной системы счисления в двоичную СС.
| 0.214 | |
| x | 2 |
| 0 | 0.428 |
| x | 2 |
| 0 | 0.856 |
| x | 2 |
| 1 | 0.712 |
| x | 2 |
| 1 | 0.424 |
| x | 2 |
| 0 | 0.848 |
| x | 2 |
| 1 | 0.696 |
| x | 2 |
| 1 | 0.392 |
Как видно из Рис.4, число 0.214 последовательно умножается на 2. Если в результате умножения получится число с целой частью, отличное от нуля, то целая часть записывается отдельно (слева от числа), а число записывается с нулевой целой частью. Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0. 0011011.
Следовательно можно записать:
Пример 8. Переведем число 0.125 из десятичной системы счисления в двоичную СС.
| 0.125 | |
| x | 2 |
| 0 | 0.25 |
| x | 2 |
| 0 | 0.5 |
| x | 2 |
| 1 | 0.0 |
Для приведения числа 0.125 из десятичной СС в двоичную, данное число последовательно умножается на 2. В третьем этапе получилось 0. Следовательно, получился следующий результат:
Пример 9. Переведем число 0.214 из десятичной системы счисления в шестнадцатеричную СС.
| 0.214 | |
| x | 16 |
| 3 | 0.424 |
| x | 16 |
| 6 | 0.784 |
| x | 16 |
| 12 | 0.544 |
| x | 16 |
| 8 | 0.704 |
| x | 16 |
| 11 | 0.264 |
| x | 16 |
| 4 | 0.224 |
Следуя примерам 4 и 5 получаем числа 3, 6, 12, 8, 11, 4. Но в шестнадцатеричной СС числам 12 и 11 соответствуют числа C и B. Следовательно имеем:
Пример 10. Переведем число 0.512 из десятичной системы счисления в восьмеричную СС.
| 0.512 | |
| x | 8 |
| 4 | 0.096 |
| x | 8 |
| 0 | 0.768 |
| x | 8 |
| 6 | 0.144 |
| x | 8 |
| 1 | 0.152 |
| x | 8 |
| 1 | 0.216 |
| x | 8 |
| 1 | 0.728 |
Пример 11. Переведем число 159.125 из десятичной системы счисления в двоичную СС. Для этого переведем отдельно целую часть числа (Пример 4) и дробную часть числа (Пример 8). Далее объединяя эти результаты получим:
Пример 12. Переведем число 19673.214 из десятичной системы счисления в шестнадцатеричную СС. Для этого переведем отдельно целую часть числа (Пример 6) и дробную часть числа (Пример 9). Далее объединяя эти результаты получим:
Перевести число 625.50 из десятичной системы в двоичную
Задача: перевести число 625.50 из десятичной системы счисления в двоичную.
Для того, чтобы перевести число 625.50 из десятичной системы счисления в двоичную, необходимо перевести вначале целую часть, а затем дробную. Таким образом потребуется:
1. Для того, чтобы перевести число 625 из десятичной системы счисления в двоичную, необходимо осуществить последовательное деление на 2, до тех пор пока остаток не будет меньше чем 2.
| — | 625 | 2 | ||
| 624 | — | 312 | 2 | |
| 1 | 312 | — | 156 | 2 |
| 0 | 156 | — | 78 | 2 |
| 0 | 78 | — | 39 | 2 |
| 0 | 38 | — | 19 | 2 |
| 1 | 18 | — | 9 | 2 |
| 1 | 8 | — | 4 | 2 |
| 1 | 4 | — | 2 | 2 |
| 0 | 2 | 1 | ||
| 0 |
Полученные остатки записываем в обратном порядке, таким образом:
2. Для перевода десятичной дроби 0.50 в двоичную систему, необходимо выполнить последовательное умножение дроби на 2, до тех пор, пока дробная часть не станет равной 0 или пока не будет достигнута заданная точность вычисления. Получаем:
Ответом станет прямая последовательность целых частей произведения. Т.е.
3. Осталось соединить переведенные части, таким образом:
Подробнее о том, как переводить числа из десятичной системы в двоичную, смотрите здесь.
Перевести число 50.10 из восьмеричной системы в двоичную
Задача: перевести число 50.10 из восьмеричной в двоичную систему счисления.
Для перевода 50.10 из восьмеричной в двоичную систему счисления, воспользуемся следующим алгоритмом:
1. Для перевода числа 50.10 в десятичную систему воспользуемся формулой:
2. Полученное число 40.125 переведем из десятичной системы счисления в двоичную. Т.к. полученное число содержит дробную часть, нам потребуется перевести вначале целую часть, а затем дробную. Таким образом необходимо:
2.1 Для того, чтобы перевести число 40 из десятичной системы счисления в двоичную, необходимо осуществить последовательное деление на 2, до тех пор пока остаток не будет меньше чем 2.
| — | 40 | 2 | ||
| 40 | — | 20 | 2 | |
| 0 | 20 | — | 10 | 2 |
| 0 | 10 | — | 5 | 2 |
| 0 | 4 | — | 2 | 2 |
| 1 | 2 | 1 | ||
| 0 |
Полученные остатки записываем в обратном порядке, таким образом:
2.2 Для перевода десятичной дроби 0.125 в двоичную систему, необходимо выполнить последовательное умножение дроби на 2, до тех пор, пока дробная часть не станет равной 0 или пока не будет достигнута заданная точность вычисления. Получаем:
0.125 ∙ 2 = 0.25 (0)
0.25 ∙ 2 = 0.5 (0)
0.5 ∙ 2 = 1 (1)
Ответом станет прямая последовательность целых частей произведения. Т.е.
2.3. Осталось соединить переведенные части, таким образом: