Пределы что такое эпсилон

Что такое предел? Что такое |Xn-A| Математика Наука

Для начала успокойтесь, я понимаю на носу экзамен, но для математики нужна «холодная голова». Сейчас мы во всем разберемся, все очень просто на самом деле 🙂

Начнем с того, что вы немного запутались в обозначениях. Последовательность принято записывать в фигурных скобках: , в то время, как ее элемент — без скобок: Xn. В первом случае n — это абстрактный номер, а во втором — это уже какой-то конкретный номер. Я могу сказать, возьмем пятый элемент последовательности , тогда n=5, то есть элемент Xn=X5, но при этом последовательность по-прежнему будет обозначаться , а не в коем случае не .

Я допускаю, что иногда лектор (учитель) опускает фигурные скобки и обзывает последовательность просто Xn, и тут уже надо понимать из контекста, где речь идет о целой последовательности, а где о ее конкретном элементе (это не сложно, как правило).

Теперь, собственно, предел. Говорим о числовых последовательностях (для нечисловых все тоже самое, только слова другие). Так как нельзя брать предел от числа — это бессмыслица, то нет нужды писать фигурные скобки в пределе : lim , пишется просто lim Xn, и имеется в виду предел последовательности (Здесь и далее, когда я пишу lim и говорю «предел последовательности», то всегда имею ввиду «при n стремящимся к бесконечности»).

Запись, lim Xn = A, значит, что при стремлении n к бесконечности, то есть вы берете все больше и больше членов последовательности и так доходите до бесконечного их числа, существует некое ЧИСЛО А, которое является пределом для этой числовой последовательности, причем А может, как являться членом , так и не являться, это никак не регулируется определением.

Вот собственно и все! Теперь вы можете попробовать посмотреть, как работает это определение на простых последовательностях, например:

2) такая, что Xn=1, для любого n, lim Xn = 1.

Обратите внимание, в первом случае предел не принадлежит последовательности, а во втором — принадлежит.

Источник

[Calculus | глава 7] Пределы, правило Лопиталя и эпсилон-дельта определение

Представляем вам седьмое видео из курса матанализа от 3Blue1Brown. В нём вы узнаете неожиданный и очень изящный способ вычислять пределы, в котором нам в очередной раз пригодятся производные, а также формальные определения производной и предела.

За выпуск благодарим:

Переводчика: Михаила Коротеева

Редактора: Николая Протасова

Диктора: Николая Протасова

Монтажера: Олега Жданова

Как же круто. Универ закончил давным-давно, забыл уже все, но послушать интересно.

[Calculus | главы 10, 11] Производные высших порядков и ряд Тейлора

Сегодня мы выпускаем целых два видео из цикла по математическому анализу от 3blue1brown!

За выпуск благодарим:

Переводчика: Михаила Коротеева

Редактора: Николая Протасова

Диктора: Николая Протасова

Монтажера: Олега Жданова

[Calculus | глава 8] Интегрирование и основная теорема матанализа

Что такое интеграл? Как считать площадь под графиком? Какое отношение к этому имеет производная?

Ответы на эти и многие другие вопросы вам покажет восьмой эпизод из цикла про матанализ от 3blue1brown: «Интегрирование и основная теорема матанализа»

За выпуск благодарим:

Переводчика: Михаила Коротеева

Редактора: Николая Протасова

Диктора: Николая Протасова

Монтажера: Олега Жданова

[Calculus | глава 6] Неявное дифференцирование — что здесь происходит?

У неявного дифференцирования свои правила.

Представляем перевод шестого видео про матанализ от 3blue1brown: «Неявное дифференцирование — что здесь происходит?»

За выпуск благодарим:

Переводчика: Михаила Коротеева

Редактора: Николая Протасова

Диктора: Николая Протасова

Монтажера: Олега Жданова

[Calculus | глава 5] Что особенного в числе Эйлера

Представляем новый перевод видео про матанализ от 3Blue1Brown — «Что особенного в числе Эйлера». Новая серия открывает долгожданную вторую часть курса матанализа от 3Blue1Brown.

За выпуск благодарим:

Переводчика: Михаила Коротеева

Редактора: Николая Протасова

Диктора: Николая Протасова

Монтажёра: Олега Жданова

[Calculus | глава 3] Формулы производных через геометрию

Почему производные вычисляются именно так? Самый наглядный способ понять это — нарисовать.

В третьем видео про матанализ речь пойдёт о том, как получить формулы производных через геометрию.

За выпуск благодарим:

Переводчика: Михаила Коротеева

Редактора: Константина Нагаева

Диктора: Михаила Коротеева

Монтажеров: Николая Протасова и Олега Жданова

[Calculus | глава 2] Парадокс производной

Производная — одно из базовых понятий матанализа, однако её определение часто остаётся для людей загадкой. Сегодня мы перевели второе видео про матанализ от 3blue1brown — про парадокс производной.

Традиционно благодарим за участие в выпуске:

Переводчика: Михаила Коротеева

Редактора: Дмитрия Сергеева

Диктора: Михаила Коротеева

Монтажеров: Николая Протасова и Олега Жданова

[Calculus | глава 1] Суть матанализа

Математический анализ является одним из важнейших разделов в математике. Мы открываем выпуск серии видео-лекций с канала 3Blue1Brown, посвященных матанализу.

В данном видео Грант Сандерсон рассказывает о сути математического анализа, раскрывая изящество математики на понятных примерах.

За участие в выпуске благодарим:

Переводчиков: Михаила Коротеева и Николая Протасова

Редактора: Ефима Мажника

Диктора: Михаила Коротеева

Монтажеров: Николая Протасова и Олега Жданова

Шутки про математику

Читает профессор лекцию по математической физике. Для упрощения записи вводит множество новых обозначений. Ближе к концу лекции ему понадобилось ввести еще одно. Он окидывает доску взглядом, задумывается на пару минут. и говорит: — Есть такая буква в грузинском алфавите.

Нейронные сети. Формулы обратного распространения

Представляем заключительную лекцию из курса по нейронным сетям от 3blue1brown. В этой лекции речь пойдет о формулах обратного распространения. Одной из важных тем, которая позволит разобраться с основными моментами дифференцирования сложных функций в контексте сетей.

Источник

СОДЕРЖАНИЕ

История

Кроме того, Ньютон иногда объяснял пределы в терминах, подобных определению эпсилон-дельта. Готфрид Вильгельм Лейбниц разработал собственное бесконечно малое и попытался дать ему прочную основу, но некоторые математики и философы все равно встретили его с беспокойством.

Неофициальное заявление

Точное заявление и связанные заявления

Точная инструкция для функций с действительным знаком

Точная инструкция для функций между метрическими пространствами

Отрицание точного утверждения

Точная формулировка пределов на бесконечности

Точная формулировка пределов на бесконечности выглядит следующим образом:

Также возможно дать определение в общих метрических пространствах.

Односторонние ограничения

и предел «слева» как

Примеры работ

Пример 1

Будет показано, что

Поскольку синус ограничен сверху единицей и снизу −1,

Пример 2

Начиная с факторинга

Таким образом, если в дальнейшем предположить, что

Пример 3

Упрощение, факторинг и деление 3 в правой части импликации дает

что сразу дает требуемый результат, если

Непрерывность

Функция f называется непрерывной в c, если она определена в c и ее значение в c равно пределу f, когда x приближается к c :

Сравнение с бесконечно малым определением

Семейство формальных определений пределов

Источник

Научный форум dxdy

Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки

Правила форума

В этом разделе нельзя создавать новые темы.

Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».

Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.

Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.

Определение предела и число эпсилон

1. Предел последовательности.
Цитирую:

2. Геометрический смысл того же предела последовательности:

Заранее благодарен за ответ.

Заслуженный участник

Заслуженный участник

Последний раз редактировалось ИСН 16.02.2013, 20:14, всего редактировалось 1 раз.

Заслуженный участник

Заслуженный участник

Заслуженный участник

Последний раз редактировалось henehen 16.02.2013, 22:34, всего редактировалось 3 раз(а).

PS. Причём, что самое интересное, такая привычка «объяснять» через левые переменные навроде эпсилонов и дельт сохраняется практически во всех учебниках и методичках, что весьма здорово способствует механическому использованию математики (не вникая ни во что) и убивает напрочь желание учиться.

И вообще, если кто-то мне объяснит человеческим языком на пальцах всю эту эпсилон-дельту технику, то я буду нечеловечески ему благодарен =)

Заслуженный участник

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Источник

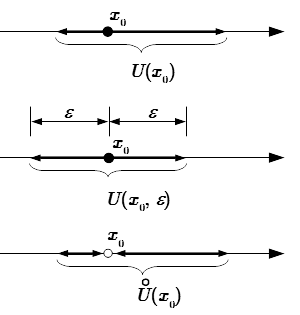
Окрестность точки

Определение окрестности точки

Окрестности конечных точек

Также широко используют понятия левосторонних, правосторонних и проколотых окрестностей конечных точек. Приводим их определения.

Проколотые окрестности конечных точек

Проколотые окрестности точки x ₀ – это те же самые окрестности, из которых исключена сама точка. Они обозначаются с кружочком над буквой. Приводим их определения.

Проколотая окрестность точки x ₀ :
.
Проколотая эпсилон окрестность точки x ₀ :
;
.
Проколотая левосторонняя окрестность :
;
.
Проколотая правосторонняя окрестность :
;
.

Окрестности бесконечно удаленных точек

Наряду с конечными точками, также вводят понятие окрестности бесконечно удаленных точек. Все они являются проколотыми, поскольку не существует бесконечно удаленного действительного числа (бесконечно удаленная точка определяется как предел бесконечно большой последовательности).

Свойство окрестности

Также справедливы и обратные утверждения.

Эквивалентность определений предела функции по Коши

Теорема
Определения предела функции по Коши, в которых используются произвольные окрестности и окрестности с равноудаленными концами эквивалентны.

Доказательство 1 ⇒ 2

Докажем, что если число a является пределом функции по 1-му определению, то оно также является пределом и по 2-му определению.

Доказательство 2 ⇒ 1

Докажем, что если число a является пределом функции по 2-му определению, то оно также является пределом и по 1-му определению.

Это означает, что число a является пределом и по первому определению.

Использованная литература:
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.

Источник