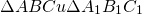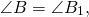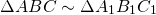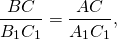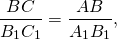Правда ли что все прямоугольные треугольники подобны

Подобие прямоугольных треугольников

Подобие прямоугольных треугольников обычно доказывают, используя не общие признаки, а специальные признаки подобия для прямоугольных треугольников.

Признаки подобия прямоугольных треугольников

1- й признак подобия прямоугольных треугольников

( подобие прямоугольных треугольников по острому углу)

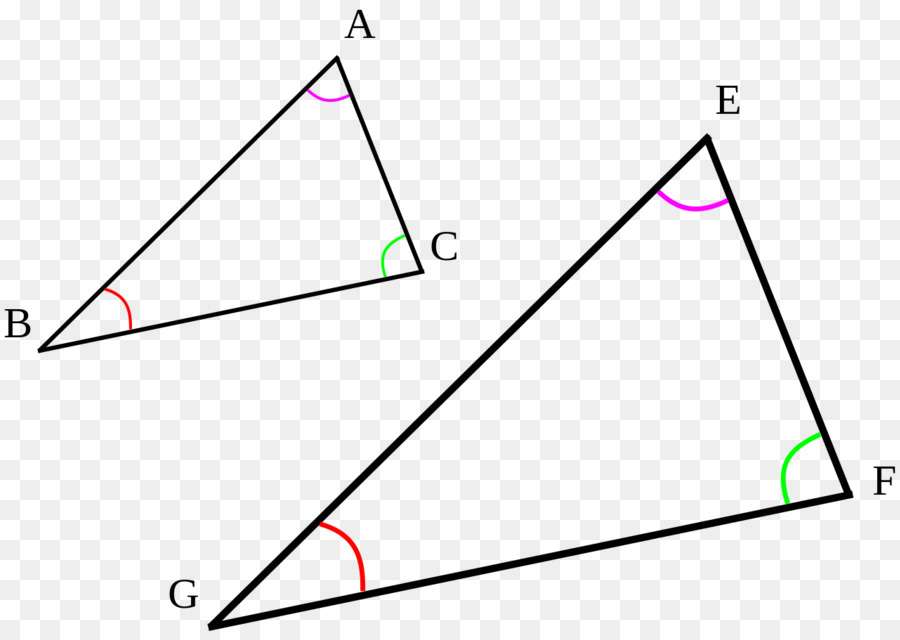
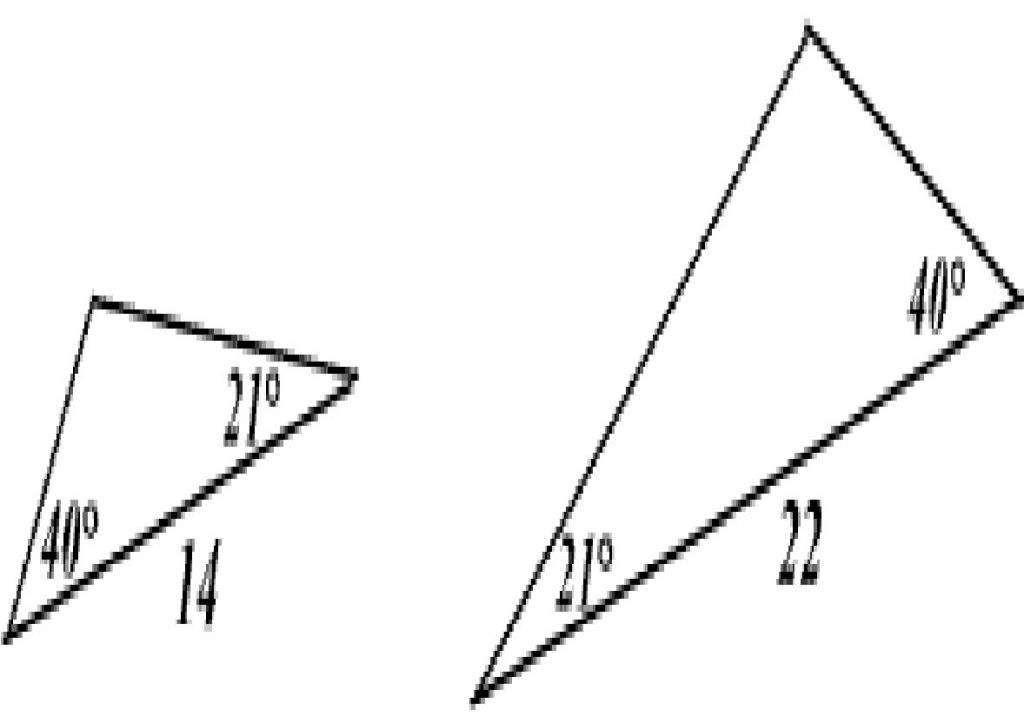
Если прямоугольные треугольники имеют равный острый угол, то такие треугольники подобны.

— прямоугольные (∠C=90º, ∠C=90º).

2- й признак подобия прямоугольных треугольников

( подобие прямоугольных треугольников по двум катетам)

Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие треугольники подобны.

— прямоугольные (∠C=90º, ∠C=90º).

3- й признак подобия прямоугольных треугольников

( подобие прямоугольных треугольников по катету и гипотенузе)

Если катет и гипотенуза одного прямоугольного треугольника пропорциональны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники подобны.

— прямоугольные (∠C=90º, ∠C=90º).

(по катету и гипотенузе).

Из подобия прямоугольных треугольников следуют соотношения между высотой, проведённой к гипотенузе, гипотенузой, катетами и проекциями катетов на гипотенузу, а также свойство биссектрисы треугольника.

Источник

Три признака подобия треугольников

Теорема 1. Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого.

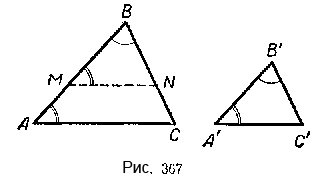
Пусть в треугольниках ABC и А’В’С ∠A = ∠А’ ∠В = ∠B’ (в подобных треугольниках вершины соответственно равных углов часто обозначают одинаковыми буквами).

Доказать, что \(\Delta\)ABС \(\sim\) \(\Delta\)А’В’С (рис. 367).

Прежде всего отметим, что из равенства двух углов данных треугольников следует, что и третьи углы их равны, т. е. ∠C = ∠С’.

Отложим от вершины В, например, на стороне AB треугольника ABC отрезок ВМ, равный отрезку А’В’. Из точки М проведём прямую MN || АС. Мы получили \(\Delta\)MBN, который подобен \(\Delta\)ABC. Но \(\Delta\)MBN = \(\Delta\)А’В’С’, так как ∠В = ∠В’ по условию теоремы; сторона MB = A’B’ по построению; ∠BMN = ∠A’ (∠BMN и ∠А’ порознь равны одному и тому же ∠А).

Если \(\Delta\)MBN \(\sim\) \(\Delta\)AВС, то \(\Delta\)А’В’С’ \(\sim\) \(\Delta\)ABC. Эта теорема выражает 1-й признак подобия треугольников.

Следствия. 1. Равносторонние треугольники подобны.

2. Равнобедренные треугольники подобны, если они имеют по равному углу при вершине или при основании.

3. Два прямоугольных треугольника подобны, если она имеют по равному острому углу.

4. Равнобедренные прямоугольные треугольники подобны.

Пусть в треугольниках ABC и А’В’С’ \(\frac = \frac\) и ∠В = ∠В’

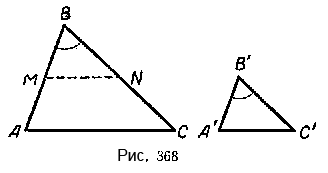
Требуется доказать, что \(\Delta\)ABC \(\sim\) \(\Delta\)А’В’С’ (рис. 368).

Для доказательства отложим, например, на стороне AB треугольника ABC от вершины В отрезок ВМ, равный отрезку А’В’. Через точку М проведём прямую MN || АС. Полученный треугольник MBN подобен треугольнику ABC.

Докажем, что \(\Delta\)MBN = \(\Delta\)А’В’С’. В этих треугольниках ∠В = ∠В’ по условию теоремы, MB = А’В’ по построению. Чтобы убедиться в равенстве сторон BN и В’С, составим пропорцию AB /_MB = BC /_BN (она вытекает из параллельности АС и MN) и сравним её с пропорцией, которая дана в условии теоремы: \(\frac = \frac\). В этих двух пропорциях имеется по три равных члена, следовательно, равны и четвёртые их члены,

т. е. В’С’ = BN. Отсюда следует равенство треугольников MBN и А’В’С’.

Так как \(\Delta\)MBN \(\sim\) \(\Delta\)А’В’С’, то, следовательно, и \(\Delta\)А’В’С’ \(\sim\) \(\Delta\)ABС.

Эта теорема выражает 2-й признак подобия треугольников.

Следствие. Прямоугольные треугольники подобны, если катеты одного из них пропорциональны катетам другого.

Теорема 3. Два треугольника подобны, если три стороны одного треугольника пропорциональны трём сторонам другого треугольника.

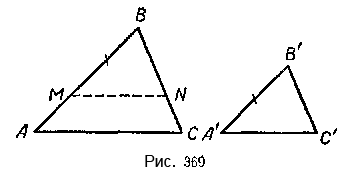
Пусть в треугольниках ABC и А’В’С’ \(\frac = \frac = \frac\) (рис. 369).

Требуется доказать, что \(\Delta\)ABC \(\sim\) \(\Delta\)А’В’С’

Для доказательства отложим на стороне AB треугольника ABC от вершины В отрезок BM = А’В’. Из точки M проведём прямую MN || АС. Полученный треугольник MBN подобен треугольнику ABC. Следовательно, \(\frac = \frac = \frac\).

Докажем, что \(\Delta\)MBN = \(\Delta\)А’В’С’. Для доказательства сравним две пропорции

\(\frac = \frac\) и \(\frac = \frac\).
В этих пропорциях имеется по три равных члена, следовательно, равны и четвёртые их члены, т.е. BN = В’С’.

Оказалось, что три стороны \(\Delta\)BMN равны трём сторонам \(\Delta\)А’В’С’, а именно:

MB = А’В’, BN = В’С’ и MN = А’С’.

Следовательно, \(\Delta\)MBN = \(\Delta\)А’В’С’, а \(\Delta\)ABC \(\sim\) \(\Delta\)А’В’С’.

Эта теорема выражает 3-й признак подобия треугольников.

Источник

Признаки подобия и равенства треугольников. Свойства подобных треугольников

Треугольник является самой простой замкнутой фигурой на плоскости. При изучении школьного курса геометрии рассмотрению его свойств уделяют особое внимание. В данной статье раскроем вопрос признаков подобия и равенства треугольников.

Какие треугольники называются подобными, а какие равными?

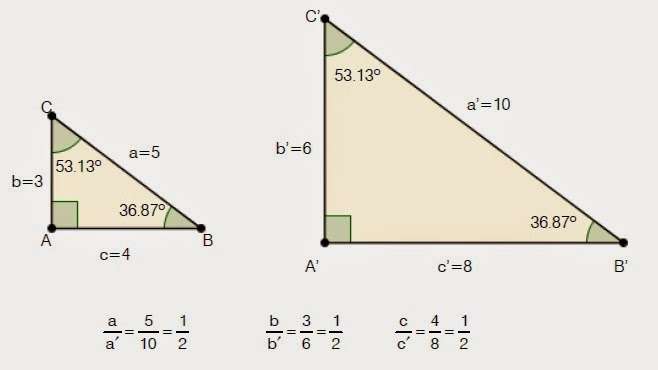
Логично предположить, что две рассматриваемые фигуры будут равны между собой, если они имеют все одинаковые углы и длины сторон. Что касается подобия, то здесь дело обстоит немного сложнее. Два треугольника будут подобны тогда, когда каждый угол одного будет равен соответствующему углу другого, а стороны, лежащие напротив равных углов обеих фигур, будут пропорциональны. Ниже изображен рисунок, на котором представлены два подобных треугольника.

Вам будет интересно: Полемизировать – это значит, спорить правильно

Признаки подобия

Говоря о свойствах и признаках подобия и равенства треугольников, следует перечислить три основных критерия, по которым можно определить, являются ли рассматриваемые фигуры подобными или нет.

Итак, две фигуры будут подобными между собой, если выполняется одно из следующих условий:

Отметим еще раз, что для доказательства подобия достаточно привести какой-либо один из представленных признаков. Логично, что все остальные будут выполняться также.

Прямоугольные треугольники: когда они подобны, а когда равны?

Говоря о признаках равенства и подобия прямоугольных треугольников, следует отметить сразу, что у каждого из них по одному углу уже равны (90o).

Последний факт приводит к следующей формулировке изложенных выше критериев подобия:

Что касается равенства треугольников с прямыми углами, то здесь просто запомнить: если два каких-либо элемента (прямой угол не считается) обеих фигур равны, то равны и сами фигуры. Например, этими двумя элементами могут быть острый угол и катет, катет и гипотенуза или гипотенуза и острый угол.

Свойства треугольников подобных

Из рассмотренных признаков подобия и равенства треугольников свойства можно выделить такие:

Оба эти свойства можно доказать самостоятельно. Суть доказательства сводится к применению математической записи подобия между сторонами фигур. Здесь приведем лишь доказательство 1-го свойства.

Пример решения задачи

Признаки подобия и равенства треугольников можно использовать для решения различных геометрических задач. Ниже приводится один из примеров.

Имеются два треугольника. У одного из них стороны равны 7,6 см, 4,18 см и 6,65 см, а у другого 3,5 см, 2,2 см и 4 см. Необходимо определить, подобны ли эти фигуры.

Поскольку даны значения трех сторон, то можно сразу проверить 3-й критерий подобия. Сложность здесь состоит в том, что нужно понять, между какими сторонами брать отношения. Тут следует воспользоваться простыми логическими рассуждениями: коэффициенты подобия могут быть равными, если делить самую маленькую сторону одного треугольника на аналогичную для другого и так далее. Поэтому имеем: 4,18 / 2,2 = 1,9; 6,65 / 3,5 = 1,9; 7,6 / 4 = 1,9. Проверив отношение всех сторон, можно с уверенностью сказать, что треугольники являются подобными, поскольку выполняется 3-й критерий.

Источник

Признаки подобия прямоугольных треугольников

Всего получено оценок: 82.

Всего получено оценок: 82.

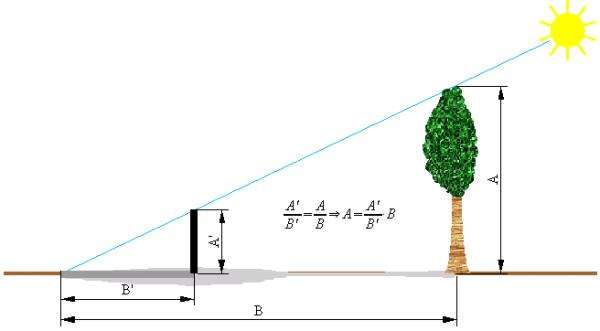
Подобие – это следующее понятие после равенства: как в математике после сложения идет умножение, так в геометрии после равенства треугольников изучают подобие. В реальной жизни подобие помогает, за счет вычислений по тени, определять реальные размеры зданий или высоких сооружений. В задачах на эту тему, благодаря подобию, можно найти значение сторон, воспользовавшись знакомым отношением.

Определения

Подобными называются треугольники, отношение сторон которых соответственно равны. Предположим треугольник АВС равен треугольнику DРН. Это значит, что:

k это коэффициент подобия.

Для обычного треугольника существует три признака подобия. Именно через них доказываются признаки подобия прямоугольных треугольников.

Первый признак подобия: по двум углам. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

Рис. 1. Первый признак подобия.

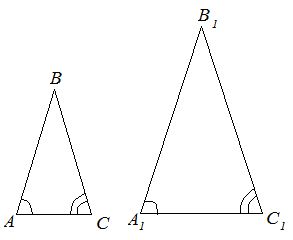
Второй признак: по трем сторонам. Если три стороны одного треугольника пропорциональны соответственным сторонам другого треугольника, то такие треугольники подобны.

Рис. 2. Второй признак подобия.

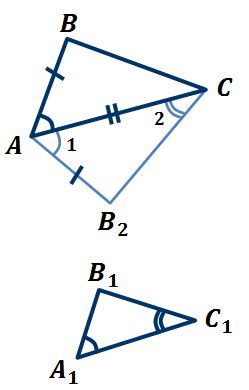
Третий признак: по двум сторонам и углу. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами равны, то такие треугольники подобны.

Рис. 3. Третий признак подобия.

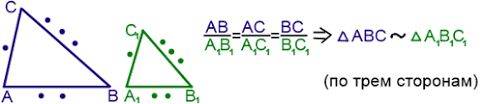
Эти определения необходимо знать, чтобы без проблем разобраться с подобием прямоугольных треугольников.

Признаки подобия прямоугольных треугольников

Доказать этот признак очень просто. Достаточно вспомнить, что прямоугольным треугольником называется треугольник, который содержит в себе прямой угол. Значит, у двух прямоугольных треугольников, один из углов всегда равен другому. А один из острых углов так же равен соответственному углу в другом треугольнике. Значит, в таких треугольниках есть два равных между собой угла, и треугольники подобны по первому признаку подобия.

$$cos(ACB)=>=>\over AC>=>$$ – то есть косинусы углов равны, оба угла острые, значит и углы равны. Тогда треугольники подобны по двум сторонам и углу между ними.

Что мы узнали?

Мы разобрали понятие подобия, выделили все определения и теоремы, необходимые для доказательства трех признаков подобия прямоугольных треугольников. Мы показали, что эти признаки лишь следствие основных, т.е. эти свойства созданы чтобы упростить и сделать быстрее решение. А это значит, что если вдруг вы забыли признаки для прямоугольного треугольника, то всегда можно воспользоваться общими.

Источник

Гомотетия. Подобные фигуры. Признаки подобия треугольников, подобие прямоугольных треугольников

Подобие – это понятие, характеризующее наличие одинаковой, не зависящей от размеров, формы у геометрических фигур.

Подобные фигуры – это фигуры, для которых существует взаимно-однозначное соответствие, при котором расстояние между любыми парами их соответствующих точек изменяется в одно и то же число раз.

Гомотетия – это преобразование подобия. Это преобразование, в котором получаются подобные фигуры (фигуры, у которых соответствующие углы равны и стороны пропорциональны).

Свойства преобразования гомотетии:

1) При гомотетии прямые переходят в прямые, полупрямые – в полупрямые, отрезки – в отрезки, углы – в углы.

2) Сохраняются углы между полупрямыми (соответственно, сохраняется параллельность прямых). Стороны гомотетичных фигур пропорциональны, а углы равны.

Подобные треугольники – это треугольники, у которых углы равны, а стороны пропорциональны.

Свойства подобных треугольников

1-й признак подобия треугольников

Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

\(\left. \begin \angle A=\angle A_1\\ \angle B=\angle B_1 \end \right \> \Rightarrow \Delta ABC \sim \Delta A_1B_1C_1\)

2-й признак подобия треугольников

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны.

3-й признак подобия треугольников

Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.

Признаки подобия прямоугольных треугольников

В треугольник AFK вписан ромб ABCD так, что угол A у них общий, а вершина C принадлежит стороне FK. Найдите сторону ромба, если AF = 21 см, AK = 24 см.

В прямоугольном треугольнике ABC с прямым углом A, сторонами AB = 4 см, BC = 8 см и высотой AK, найдите отрезки KB и KC.

Прямая, параллельная основанию треугольника, делит его на треугольник и трапецию, площади которых относятся как 4:5. Периметр образовавшегося треугольника равен 20 см. Найдите периметр данного треугольника.

Источник