Правда ли что смежные углы всегда равны

Смежные углы всегда равны

Здравствуйте!
Смежные углы всегда равны. Правда или нет? Помогите найти ответ на этот вопрос.
Спасибо!

Чтобы ответить на заданный вопрос о том, что смежные углы всегда равны, сначала рассмотрим само понятие смежных углов.
Представим себе развернутый угол. Градусная мера такого угла равна 180 градусов. Или же можно просто провести прямую и из любой ее точки провести луч. Получим два угла, одна из сторон каждого из них будет частью исходной прямой, а другая сторона будет их общей и будет являться проведенным лучом.

Как говорилось в начале, развернутый угол равен 180 градусов. Поэтому сумма градусных мер полученных из него смежных углов также будет равна 180 градусов.
Если обозначить величину одного из смежных углов буквой а, то величина второго смежного угла будет равна 180 – а.
Теперь ответим на вопрос правда или нет, что смежные углы всегда равны.
Чтобы смежные углы были равны, необходимо, чтобы выполнялось условие (исходя из выше изложенного):
а = 180 – а.
найдем значения углов, при которых они будут равными. Для этого решим данное простое уравнение:
а + а = 180
2а = 180
а = 180 / 2
а = 90
Величина первого угла найдена – это 90 градусов.
Найдем величину второго угла:
180 – а = 180 – 90 = 90 (градусов).
Получаем, что смежные углы будут равными только в случае, когда оба будут одновременно равны по 90 градусов.
Но провести луч к исходной прямой можно под любым градусом, тогда соответственно смежные углы равными между собой не будут.
Ответом на заданный вопрос будет НЕТ. Смежные углы будут равны только если будут прямыми.

Источник

Смежные углы

Что такое смежные углы? Какие у них свойства?

Определение.

Смежные углы — это углы, у которых одна сторона — общая, а другие стороны лежат на одной прямой.

∠1 и ∠2 — смежные углы

Сколько смежных углов образуется при пересечении двух прямых?

При пересечении двух прямых образуется четыре пары смежных углов:

Но, так как ∠1 =∠4, ∠2=∠3 (как вертикальные), то достаточно рассмотреть только одну из этих пар.

Свойство смежных углов.

Сумма смежных углов равна 180º.

1) Даны два смежных угла. Один на 42 градуса больше другого. Найти эти углы.

∠AOC и ∠BOC — смежные,

∠AOC на 42º больше, чем ∠BOC

Пусть ∠BOC=хº, тогда ∠AOC= х+42º. Так как сумма смежных углов равна 180º, то ∠BOC+∠AOC=180º.

Значит, ∠BOC= 69º, ∠AOC=69+42=111º.

2) Найти смежные углы, если их градусные меры относятся как 4:5.

Значит, смежные углы равны 4∙20=80º и 5∙20=100º.

3) Один из углов, образованных при пересечении двух прямых, в 5 раз больше другого. Найти эти углы.

Дано: AB и CD — прямые, O — точка их пересечения,

∠AOD в 5 раз больше, чем ∠BOD

При пересечении двух прямых образуются смежные и вертикальные углы. Так как вертикальные углы равны между собой, то углы∠AOD и ∠BOD — смежные. Пусть ∠BOD=xº, тогда ∠AOD=5xº. Так как сумма смежных углов равна 180º, ∠AOD +∠BOD=180º.

Значит, ∠BOD=30º, ∠AOD=5∙30=150º.

Могут ли смежные углы быть равными?

Да. Если смежные углы равны между собой, то, так как сумма смежных углов равна 180º, каждый из них равен половине суммы, то есть 90º.

угол, смежный с прямым, есть прямой угол.

Могут ли два смежных угла быть тупыми? Острыми?

Нет. Так как градусная мера тупого угла больше 90º, то сумма двух тупых углов больше 180º. А сумма смежных углов равна 180º.

Градусная мера острого угла меньше 90º. Значит, сумма двух острых углов меньше 180º.

Таким образом, в паре смежных углов один — тупой, другой — острый (или оба прямые).

Источник

Смежные углы всегда равны верно или нет

Здравствуйте!
Верно или нет, что смежные углы всегда равны? Что такое смежные углы?
Спасибо!

Начнем разбор вопроса верно или нет, что смежные углы всегда равны с ответа на вопрос, какие из углов носят название смежных.
Представьте себе два угла, у которых одна сторона одного из них совпадает с одной из сторон второго угла. Кроме того остальные две стороны обоих углов составляют развернутый угол (то есть их градусная мера = 180 градусов).

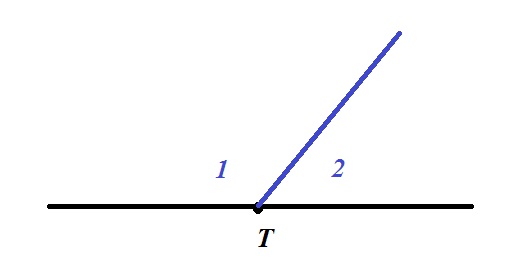
На представленном выше рисунке углы 1 и 2 – смежные. У этих двух углов одна общая сторона, изображенная синим цветом, а две оставшиеся стороны представленных углов представляют собой развернутый угол. Таким образом, сумма двух смежных углов будет всегда равняться 180 градусам.
Теперь вернемся к основному вопросу.
Как видно из рисунка, смежные углы не всегда равны. Поэтому рассматриваемое утверждение является неверным.
Но все же существует вариант, когда смежные углы будут равными. Этот вариант легко просчитать, разделив сумму смежных углов на две равные части. Тогда получим, что смежные углы будут равны только тогда, если каждый из них будет равен 180 / 2 = 90 градусов, то есть если оба смежных угла будут прямыми.
Таким образом, смежные углы равны будут не всегда, а только в том случае, когда они будут прямыми.
Чтобы лучше запомнить, что такое смежные углы, можно ассоциировать их со смежными комнатами, что довольно часто используется в быту.

Источник

Углы. Смежные углы.

Какие углы называются смежными?

Смежными углами называется пара углов с общей вершиной и одной

общей стороной. 2 оставшиеся стороны делают продолжение друг

другу, образовывая прямую линию. Для угла 135 градусов смежным

будет угол равный 45 градусам. Для угла x градусов смежным

является угол (180 – x) градусов.

Два смежных угла — это углы, с одной общей стороной, а остальные стороны находятся на одной прямой.

При пересечении 2-х прямых получается 4-ре пары смежных углов:

Но, так как ∠1 =∠4, ∠2 = ∠3 (как вертикальные), то достаточно рассматривать

только одну из этих пар.

Свойство смежных углов.

Чему равна сумма смежных углов?

Смежные углы равны: сумма смежных углов 180º.

Следствия из теоремы о смежных углах.

Тригонометрические соотношения.

противоположные знаки (исключение неопределенные значения).

Задание. Чему будет равна градусная мера угла α, когда градусная мера смежного ему угла = 70°?

Как найти смежный угол?

Решение. Из теоремы о смежных углах находим:

Источник

Правда ли что смежные углы всегда равны

Укажите номера верных утверждений.

1) Если три угла одного треугольника равны трем углам другого треугольника, то такие треугольники подобны.

2) Сумма смежных углов равна 180°.

3) Любая медиана равнобедренного треугольника является его биссектрисой.

Проверим каждое из утверждений.

1) «Если три угла одного треугольника равны трем углам другого треугольника, то такие треугольники подобны» — верно, по первому признаку подобия треугольнииков.

2) «Сумма смежных углов равна 180°» — верно, по свойству смежных углов.

3) «Любая медиана равнобедренного треугольника является его биссектрисой» — неверно; верным будет утверждение: «Любая медиана равностороннего треугольника является его биссектрисой».

Укажите номера верных утверждений.

1) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.

2) Смежные углы равны.

3) Медиана равнобедренного треугольника, проведённая к его основанию, является его высотой.

Проверим каждое из утверждений.

1) «Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны» — верно, по второму признаку подобия треугольников.

2) «Смежные углы равны» — неверно, два смежных углы и связаны соотоношением: .

3) «Медиана равнобедренного треугольника, проведённая к его основанию, является его высотой» — верно, по свойству равнобедренного треугольника.

Укажите номера верных утверждений.

1) Смежные углы равны.

2) Любые две прямые имеют ровно одну общую точку.

3) Если угол равен 108°, то вертикальный с ним равен 108°.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Смежные углы равны» — неверно, смежные углы и связаны соотношением: .

2) «Любые две прямые имеют ровно одну общую точку» — неверно, прямые могут также быть параллельны, тогда точек пересечения нет, или совпадать, тогда точек пересечения бесконечно много.

3) «Если угол равен 108°, то вертикальный с ним равен 108°» — верно по свойству вертикальных углов.

Аналоги к заданию № 41: 316233 Все

Укажите номера верных утверждений.

1) Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то треугольники подобны.

2) Сумма смежных углов равна 180°.

3) Любая высота равнобедренного треугольника является его биссектрисой.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то треугольники подобны» — верно, по признаку подобия треугольников.

2) «Сумма смежных углов равна 180°» — верно по свойству смежных углов.

3) «Любая высота равнобедренного треугольника является его биссектрисой» — неверно, это утверждение справедливо только для равностороннего треугольника.

Аналоги к заданию № 93: 171 197 311684 357582 Все

Укажите номера верных утверждений.

1) Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то треугольники подобны.

2) Сумма смежных углов равна 180°.

3) Любая высота равнобедренного треугольника является его биссектрисой.

Проверим каждое из утверждений.

1) «Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то треугольники подобны» — верно, по третьему признаку подобия треугольников.

2) «Сумма смежных углов равна 180°» — верно, по теореме о смежных углах.

3) «Любая высота равнобедренного треугольника является его биссектрисой» — неверно, верным будет являться утверждение «Высота равнобедренного треугольника, проведённая к его основанию, является его биссектрисой».

Какое из следующих утверждений верно?

1) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.

2) Смежные углы равны.

3) Каждая из биссектрис равнобедренного треугольника является его высотой.

Проверим каждое из утверждений.

1) «Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.» — верно, если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.

2) «Смежные углы равны.» — неверно, сумма смежных углов равна 180°.

3) «Каждая из биссектрис равнобедренного треугольника является его высотой.» — неверно, только одна биссектриса равнобедренного треугольника является его высотой.

Какие из следующих утверждений верны?

1) Треугольника со сторонами 1, 2, 4 не существует.

2) Смежные углы равны.

3) Все диаметры окружности равны между собой.

Если утверждений несколько, запишите их номера в порядке возрастания.

1) «Треугольника со сторонами 1, 2, 4 не существует» — верно, большая сторона треугольника должна быть меньше суммы двух других.

2) «Смежные углы равны» — неверно, смежные углы и связаны соотношением: .

3) «Все диаметры окружности равны между собой» — верно.

Какое из следующих утверждений верно?

1) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.

2) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.

3) Смежные углы равны.

Если утверждений несколько, запишите их номера в порядке возрастания.

1) «Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой» — верно, это аксиома планиметрии.

2) «Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны» — неверно: например, могут быть квадрат и ромб с равной длиной стороны.

3) «Смежные углы равны» — неверно, смежные углы и связаны соотношением: .

Окружность проходит через вершины А и С треугольника АВС и пересекает его стороны АВ и ВС в точках К и Е соответственно. Отрезки АЕ и СК перпендикулярны. Найдите ∠КСВ, если ∠АВС = 20°.

Углы АКС и АЕС равны, т. к. опираются на одну дугу окружности; следовательно, ∠ВКС = ∠ВЕА, как смежные с ними. Из четырёхугольника ВКDЕ: Из ВКС: ∠КСВ = 180° − 125° − 20° = 35°.

Какое из следующих утверждений верно?

1. Всегда один из двух смежных углов острый, а другой тупой.

2. Площадь квадрата равна произведению двух его смежных сторон.

3. Все хорды одной окружности равны между собой.

В ответ запишите номер выбранного утверждения.

Рассмотрим каждое из утверждений:

Какое из следующих утверждений верно?

1) В прямоугольном треугольнике гипотенуза равна сумме катетов.

2) Всегда один из двух смежных углов острый, а другой тупой.

3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.

В ответ запишите номер выбранного утверждения.

Рассмотрим каждое из утверждений:

1) «В прямоугольном треугольнике гипотенуза равна сумме катетов» — неверно, по теореме Пифагора в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

2) «Всегда один из двух смежных углов острый, а другой тупой» — неверно, так как сумма смежных углов равна 180°, следовательно, если один из углов прямой, то смежный ему будет тоже прямой.

3) «Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности» — верно по свойству окружности.

Какие из следующих утверждений верны?

1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.

2) Если угол равен 60°, то смежный с ним равен 120°.

3) Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70° и 110°, то эти две прямые параллельны.

4) Через любые три точки проходит не более одной прямой.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.» — неверно, если при пересечении двух прямых третьей прямой внутренние накрестлежащие углы равны, то эти две прямые параллельны. Если внутренние накрестлежащие углы составляют в сумме 90°, то они могут быть не равны.

2) «Если угол равен 60°, то смежный с ним равен 120°.» — верно, сумма смежных углов равна 180°.

3) «Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70° и 110°, то эти две прямые параллельны.» — верно, если при пересечении двух прямых третьей прямой внутренние односторонние углы составляют в сумме 180°, то эти две прямые параллельны.

4) «Через любые три точки проходит не более одной прямой.» — верно, через три точки либо нельзя провести прямую, если они не лежат на одной линии, либо можно, но только одну.

Какие из следующих утверждений верны?

1) Смежные углы всегда равны.

2) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.

3) Любые два равносторонних треугольника подобны.

В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

1) Смежные углы всегда равны. — неверно, сумма смежных углов равна 180°.

2) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой. — верно.

3) Любые два равносторонних треугольника подобны. — верно, они подобны по второму признаку подобия.

Какое из следующих утверждений верно?

1) Смежные углы всегда равны.

2) Каждая из биссектрис равнобедренного треугольника является его высотой.

3) Существует прямоугольник, диагонали которого взаимно перпендикулярны.

Проверим каждое из утверждений.

1) «Смежные углы равны» — неверно, смежные углы и связаны соотношением: .

2) «Каждая из биссектрис равнобедренного треугольника является его высотой» — неверно, верным будет являться утверждение: «Каждая из биссектрис равностороннего треугольника является его высотой».

3) «Существует прямоугольник, диагонали которого взаимно перпендикулярны.» — верно, такой прямоугольник — это квадрат.

Какие из данных утверждений верны? Запишите их номера.

2) В любой треугольник можно вписать окружность.

3) Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.

Проверим каждое из утверждений.

2) «В любой треугольник можно вписать окружность» — верно, по свойству треугольника.

3) «Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом» — верно, поскольку если его смежные стороны равны, то и все его стороны равны..

Какие из данных утверждений верны? Запишите их номера.

1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.

2) Диагональ трапеции делит её на два равных треугольника.

3) Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон.

Проверим каждое из утверждений.

1) «Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны» — верно, по признаку параллельности прямых.

2) «Диагональ трапеции делит её на два равных треугольника» — неверно, верным будет утверждение «Диагональ параллелограмма делит его на два равных треугольника».

3) «Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон» — верно, по теореме Пифагора.

Укажите номера верных утверждений.

1) Если угол равен 47°, то смежный с ним равен 153°.

2) Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны.

3) Через любую точку проходит ровно одна прямая.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Если угол равен 47°, то смежный с ним равен 153°» — неверно, сумма смежных углов равна 180°.

2) «Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны» — верно, по признаку параллельности прямых.

3) «Через любую точку проходит ровно одна прямая» — неверно через одну точку проходит бесконечное множество прямых.

Не следует думать, что вопрос «какие утверждения верные?» подразумевает, что в ответе должно быть несколько утверждений. Так же, как задача «решите уравнение» не подразумевает, что решение вообще есть.

Укажите номера верных утверждений.

1) Любые три прямые имеют не более одной общей точки.

2) Если угол равен 120°, то смежный с ним равен 120°.

3) Если расстояние от точки до прямой больше 3, то и длина любой наклонной, проведённой из данной точки к прямой, больше 3.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Любые три прямые имеют не более одной общей точки» — верно. Если прямые имеют две и более общих точек, то они совпадают. (См. комментарии к задаче.)

2) «Если угол равен 120°, то смежный с ним равен 120°» — неверно. Сумма смежных углов равна 180°.

3) «Если расстояние от точки до прямой больше 3, то и длина любой наклонной, проведённой из данной точки к прямой, больше 3» — верно. Т. к. расстояние — длина кратчайшего отрезка до прямой, а все наклонные — длиннее.

Аналоги к заданию № 311851: 316323 316349 316375 Все

В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ВАС. Ответ дайте в градусах.

Сумма смежных углов равна 180°, поэтому В равнобедренном треугольнике углы при основании равны, следовательно,

Аналоги к заданию № 37: 311680 340586 Все

Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции.

Запишите величины углов в ответ без пробелов в порядке неубывания.

Пусть углы трапеции равны и угол Около выпуклого четырёхугольника можно описать окружность тогда и только тогда, когда сумма противоположных углов равна 180°: откуда Сумма смежных углов в трапеции равна 180°, следовательно, Тем самым, три неизвестных угла равны 49°, 131° и 131°.

Источник