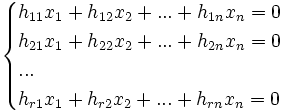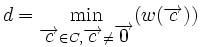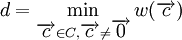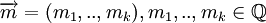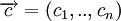порождающая матрица линейного блокового кода применяемого для помехоустойчивого кодирования
Порождающие матрицы блочных кодов
Только что в качестве примера были рассмотрены простейшие корректирующие коды — код с простой проверкой на четность, позволяющий обнаруживать однократную ошибку в принятой последовательности, а также блочный итеративный код и «облачный» код, исправляющие одну ошибку с помощью набора проверок на четность. Во всех кодах в процессе помехоустойчивого кодирования формировались дополнительные разряды, присовокупляемые к исходной кодовой комбинации.
Зададим формальные (порождающие) правила, по которым осуществляется кодирование, т.е. преобразование информационной последовательности в кодовое слово.
Простейшим способом описания, или задания, корректирующих кодов является табличный способ, при котором каждой информационной последовательности просто назначается кодовое слово из таблицы кода. Например, для простейшего кода с проверкой на четность таблица соответствия исходных и кодовых комбинаций будет следующей:
Такой способ описания кодов применим для любых, а не только линейных кодов. Однако, при больших к размер кодовой таблицы оказывается слишком большим, чтобы им пользоваться на практике.
Другим способом задания линейных блочных кодов является использование так называемой системы порождающих уравнений, определяющих правило, по которому символы информационной последовательности преобразуются в кодовые символы. Для того же примера система порождающих уравнений будет выглядеть следующим образом:
Однако наиболее удобным и наглядным способом описания линейных блочных кодов является их задание с использованием порождающей матрицы, являющейся компактной формой представления системы проверочных уравнений.
Линейный блочный (л, /с)-код полностью определяется матрицей G размером к х п с двоичными матричными элементами. При этом каждое кодовое слово является линейной комбинацией строк матрицы G, а каждая линейная комбинация строк G — кодовым словом.
Линейные блочные коды, задаваемые порождающими матрицами, будем называть матричными кодами. Обычное (каноническое) представление порождающей матрицы выглядит так:
Например, для простейшего (4, 3)-кода с проверкой на четность порождающая матрица будет иметь вид:
Тогда соответствующим ему кодовым словом U будет
С учетом структуры матрицы G символы кодового слова и будут такими:
Например, если входная последовательность кодера т = = (10 1), то с применением порождающей матрицы код будет построен так:
8 Командир послал трех разведчиков по первой дороге, трех — по второй, двух — по третьей, по четвертой пошел сам. Составить порождающую матрицу такого кода.
Ответ: по сюжету задачи сообщение, полученное командиром лично, не может быть искаженным. Поэтому ограничимся исследованием информации, передаваемой бойцами. В группе, отправившейся по одной из дорог, каждый боец должен доложить командиру либо об обнаружении объекта (обозначим такой доклад «1»), либо об отсутствии объекта («0»). При отсутствии искажений доклады каждого бойца из одной и той же группы должны совпадать. Следовательно:
Матрицу можно привести к каноническому виду, перенумеровав бойцов, т.е. по первой дороге послав первого, четвертого и пятого, по второй дороге — второго, шестого и седьмого, по третьей дороге—третьего и восьмого бойцов. Получим следующую порождающую матрицу:
Определенный таким образом код называется линейным блочным систематическим (п, /cj-кодом с обобщенными проверками на четность.
М Вернер Основы кодирования
Глава 2. Линейные блоковые коды
2.1. Помехоустойчивое кодирование
Реальные системы передани данных не совершенны. Применяя информационную технику, мы должны учитывать возможность возникновения ошибок (вероятность ошибок) при передаче и хранении информации. Это в первую очередь относится к
• передаче данных при ограниченной мощности сигнала (спутниковая и мобильная связь)
• передаче информации но сильно зашумленным каналам (мобильная связь, высокоскоростные проводные линии связи)
• каналам связи с повышенными требованиями к надежности информации (вычислительные сети, линии передачи со сжатием данных)
Во всех вышеперечисленных случаях используются коды, контролирующие ошибки. Теория помехоустойчивого кодирования для каждого конкретного канала позволяет выбрать наиболее эффективный метод обнаружения и исправления ошибок. Существуют два взаимодополняющих метода борьбы с помехами.
• Кодирование для обнаружения ошибок приемник распознает ошибки и, в случае необходимости, производит запрос на повторную передачу ошибочного блока.
В последующих разделах идеи помехоустойчивого кодирования будут подробно объяснены на примерах линейных блоковых кодов. Здесь же мы рассмотрим простейшую модель передачи данных с использованием помехоустойчивого кодирования (рис. 2.1).
Рис. 2.1. Модель канала связи с кодированием.
Будем исходить из того, что при передаче информации используется блоковый код Хэмминга*, структура которого будет подробно раскрыта в дальнейшем. Сейчас мы ограничимся его табличным описанием. Пусть кодер источника последовательно выдает информационные слова фиксированной длины. Кодер канала заменяет каждое информационное слово u кодовым словом v в соответствии с табл. 2.1.
* Ричард В. Хэмминг: 1915/1998. американский математик.
Таблица 2.1. Кодовая таблица (7,4)-кода Хэмминга.
Декодер сравнивает принятое слово r со всеми кодовыми словами табл. 2.1. Если слово r совпадает с одним из кодовых слов, то соответствующее информационное слово и выдается потребителю. Если r отличается от всех кодовых слов, то в канале произошла обнаруживаемая ошибка.*
* Из структуры кода Хэмминга следует одно интересное свойство, которое может быть проверенно простым перебором:
Для любого произвольного вектора г существует ближайшее кодовое слово, которое или полностью совпадает с г или отличается от него только в одном двоичном разряде. Таким образом, если в векторе v при передаче по каналу произошла только одна ошибка, она всегда может быть исправлена в процессе декодирования,- Прим. перев.
Из всего вышесказанного уже можно сделать два важных вывода:
• Если в процессе передачи по зашумлснному каналу кодовое слово отобразится в другое кодовое слово, не совпадающее с переданным, то происходит необнаружимая ошибка. Назовем ее остаточной ошибкой декодирования.
• «Хорошие коды» обладают некоторой математической структурой, которая позволяет эффективно распознать, а в некоторых случаях и исправлять ошибки, возникающие при передаче информации по каналу связи.
2.2. Порождающая матрица
Важное семейство кодов образуют линейные двоичные блоковые, коды. Эти коды замечательны тем, что представляя информационные и кодовые слова в форме двоичных векторов, мы можем описать процессы кодирования и декодирования с помощью аппарата линейной алгебры, при этом, компонентами вводимых векторов и матриц являются символы 0 и 1. Операции над двоичными компонентами производятся по привычным правилам двоичной арифметики, так называемой, арифметики по модулю 2 (Табл. 2.2).
Таблица 2.2. Арифметика по модулю 2.
Вместо k бит информационного вектора в канал передается n бит кодового вектора. В этом случае говорят об избыточном кодировании со скоростью
Чем ниже скорость, тем больше избыточность кода и тем большими возможностями для защиты от ошибок он обладает (здесь, однако, надо учитывать, что с увеличением избыточности, затраты на передачу информацию также возрастают).
Таким образом, кодовое слово v и информационное слово и связаны соотношением
Например, информационный вектор и = (1010) отображается в кодовый вектор
Первое, что сразу же бросается в глаза из табл. 2.1, это совпадение последних четырех разрядов кодовых слов с информационными векторами. Такой код относится к семейству систематических кодов.
Коды, в которых информационное слово может быть непосредственно выделено из соответствующего ему кодового вектора, называются систематическими.
Порождающую матрицу любого систематического кода всегда можно путем перестановки столбцов привести к виду
Замечание. В литературе часто единичная матрица ставится на первое место. Заметим, что перестановка столбцов матрицы не оказывает никакого влияния на корректирующую способность кода.
Таким образом, в кодовом векторе систематического кода всегда можно выделить информационные и проверочные символы
Роль проверочных символов и их использование будут подробно разъяснены в следующих разделах.
2.3. Синдромное декодирование
Задача декодера заключается в том, чтобы используя структуру кода, по принятому слову г. восстановить переданный информационный вектор.
Таким образом, из первых трех столбцов порождающей матрицы G (2.2), мы получили систему трех проверочных уравнений, в которой операция производится по правилам арифметики по модулю 2 (см. табл. 2.2). Если в полученной системе уравнений хотя бы одна из компонент не равна нулю, то в канале произошла ошибка.
Запишем систему проверочных уравнений в общем виде. Для любого систематического кода с порождающей матрицей (2.5), проверочная матрица определяется как
Вектор s принято называть синдромом. Таким образом, ошибка будет обнаружена, если хотя бы одна из компонент s не равна нулю. Равенство (2.9) можно переписать в виде
Замечание. В медицине термин синдром используется для, обозначения сочетания признаков, характеризующих определенное болезненное состояние организма.
Пример: Синдромное декодирование (7, 4)-кода Хэмминга.
Используя (2.5) и (2.8), построим проверочную матрицу из порождающей матрицы кода Хэмминга (2.2). Она имеет вид
При передаче информационного слова и = (1010) по каналу без шума r = v = (0011010). Можем убедиться, что в этом случае синдром равен
Если, например, в кодовом слове произошла одиночная ошибка на четвертой позиции ( r = (0010010)), то синдромом является четвертая строка транспонированной проверочной матрицы
Таблица 2.3. Таблица синдромов однократной ошибки (7.4)-кода Хэмлинга.
Обобщим приведенные выше рассуждения, используя аппарат линейной алгебры.
Рис. 2.3. Структура кодовых векторных пространств.
Заметим, что порождающая матрица может быть разложена на матрицу Р и единичную матрицу I только в случае систематических кодов.
причем, правая часть равенства справедлива только для систематических кодов.
При синдромном кодировании приемник использует свойство ортогональности кодов
Таким образом, для каждого кодового слова v е С справедливо
Каждому принятому слову, не принадлежащему коду, соответствует отличный от нуля синдром
В рассмотренном выше примере, единичной ошибке в четвертом разряде соответствует вектор е = (0001000).
Рис. 2.4. Модель передачи информации на двоичном уровне.
В силу свойств линейности и ортогональности векторов имеем
Последнее равенство является основой синдромного декодирования. В процессе декодирования могут возникнуть следующие ситуации:
Случай 1.1: е = 0 безошибочная передача информации;
Случай 2: ошибка будет обнаружена при декодировании.
Ясно, что в первом случае, декодер всегда выдает принятое слово r потребителю, при этом существует некоторая вероятность неисправления ошибки. Во втором случае возможны два режима работы декодера.
• Распознавание ошибок. Декодер всегда определяет наличие ошибки в принятом векторе г. В зависимости от требований потребителя, принятое информационное слово или «стирается», или производится запрос на его повторную передачу.
• Коррекция ошибок. Корректирующая способность декодера может быть пояснена на примере (7,4)-кода Хэмминга, рассмотренного выше.
Декодер может выдавать потребителю ошибочное информационное слово тогда и только тогда, когда в канале произошли необнаружимые ошибки, или кратность канальной ошибки превышает корректирующую способность кода. Из рассмотренного выше примера следует, что эффективность конкретного кода зависит от области его применения и, в особенности, от канала связи. Если мы передаем информацию по каналу с аддитивным белым гауссовским шумом (АБГШ), то ошибки в кодовом слове независимы. Если при этом отношение сигнал/шум достаточно велико, то вероятность одиночной ошибки во много раз превышает вероятность ошибок высших кратностей, поэтому, использование в таком канале кода Хэмминга с исправлением однократной ошибки может оказаться весьма эффективным. С другой стороны, в каналах, где преобладают многократные ошибки (например, в каналах с замираниями), исправление одиночных ошибок лишено смысла. При практическом выборе конкретного помехоустойчивого кода необходимо также учитывать скорость его декодирования и сложность технической реализации.
Порождающая матрица
В области математики и теории информации линейный код — это важный тип блокового кода, использующийся в схемах определения и коррекции ошибок. Линейные коды, по сравнению с другими кодами, позволяют реализовывать более эффективные алгоритмы кодирования и декодирования информации.
Содержание
Основы
В процессе хранения данных и передачи информации по сетям связи неизбежно возникают ошибки. Контроль целостности данных и исправление ошибок — важные задачи на многих уровнях работы с информацией (в частности, физическом, канальном, транспортном уровнях модели OSI).
В системах связи возможны несколько стратегий борьбы с ошибками:
Коды обнаружения и исправления ошибок
Корректирующие коды — коды, служащие для обнаружения или исправления ошибок, возникающих при передаче информации под влиянием помех, а также при её хранении.
Для этого при записи (передаче) в полезные данные добавляют специальным образом структурированную избыточную информацию, а при чтении (приеме) её используют для того, чтобы обнаружить или исправить ошибки. Естественно, что число ошибок, которое можно исправить, ограничено и зависит от конкретного применяемого кода.
С кодами, исправляющими ошибки, тесно связаны коды обнаружения ошибок. В отличие от первых, последние могут только установить факт наличия ошибки в переданных данных, но не исправить её.
В действительности, используемые коды обнаружения ошибок принадлежат к тем же классам кодов, что и коды, исправляющие ошибки. Фактически, любой код, исправляющий ошибки, может быть также использован для обнаружения ошибок (при этом он будет способен обнаружить большее число ошибок, чем был способен исправить).
По способу работы с данными коды, исправляющие ошибки делятся на блоковые, делящие информацию на фрагменты постоянной длины и обрабатывающие каждый из них в отдельности, и сверточные, работающие с данными как с непрерывным потоком.
Блоковые коды
Если исходные k бит код оставляет неизменными, и добавляет n − k проверочных, такой код называется систематическим, иначе несистематическим.
Задать блоковый код можно по-разному, в том числе таблицей, где каждой совокупности из k информационных бит сопоставляется n бит кодового слова. Однако, хороший код должен удовлетворять, как минимум, следующим критериям:
Нетрудно видеть, что приведенные требования противоречат друг другу. Именно поэтому существует большое количество кодов, каждый из которых пригоден для своего круга задач.
Практически все используемые коды являются линейными. Это связано с тем, что нелинейные коды значительно сложнее исследовать, и для них трудно обеспечить приемлемую легкость кодирования и декодирования.
Линейные пространства
Порождающая матрица
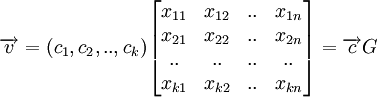
где 
Это соотношение устанавливает связь между векторами коэффициентов 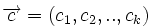
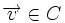
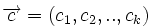
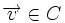
Проверочная матрица
Другим способом задания линейных пространств является описание через проверочную матрицу.
Тогда любой вектор 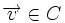
Или в матричной форме: 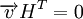
где 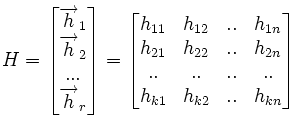
Приведенную систему линейных уравнений следует рассматривать, как систему проверок для всех векторов линейного пространства, поэтому матрица 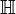
Формальное определение
Линейный код длины n и ранга k является линейным подпространством C размерности k векторного пространства 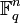
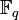
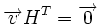
Свойства и важные теоремы
Минимальное расстояние и корректирующая способность
Расстоянием Хемминга (метрикой Хемминга) между двумя кодовыми словами 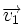
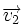
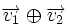
Минимальное расстояние d линейного кода является минимальным из всех расстояний Хемминга всех пар кодовых слов.
Вес вектора — w расстояние Хемминга между этим вектором и нулевым вектором, иными словами — число ненулевых компонент вектора.
Минимальное расстояние d линейного кода равно минимальному из весов Хемминга ненулевых кодовых слов:
Расстояние между двумя векторами 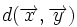
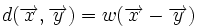
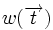
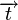
Минимальное расстояние Хемминга d является важной характеристикой линейного блокового кода. Она определяет другую, не менее важную характеристику — корректирующую способность:
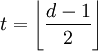
Корректирующая способность определяет, какое максимальное число ошибок в одном кодовом слове код может гарантированно исправить.
Поясним на примере. Предположим, что есть два кодовых слова A и B, расстояние Хемминга между ними равно 3. Если было передано слово A, и канал внес ошибку в одном бите, она может быть исправлена, так как даже в этом случае принятое слово ближе к кодовому слову A, чем B. Но если каналом были внесены ошибки в двух битах, декодер может посчитать, что было передано слово B.
Число обнаруживаемых ошибок — число ошибок, при котором код может судить об ошибочной ситуации. Это число равно
Теорема 2 (без доказательства):
Если любые l столбцов проверочной матрицы H линейного (n, k)-кода линейно независимы, то минимальное расстояние кода равно по меньшей мере d. Если при этом найдутся d линейно зависимых столбцов, то минимальное расстояние кода равно d в точности.
Теорема 3 (без доказательства):
Если минимальное расстояние линейного (n, k)-кода равно d, то любые l столбцов проверочной матрицы H линейно независимы и найдутся d линейно зависимых столбцов.
Коды Хемминга
Коды Хемминга — простейшие линейные коды с минимальным расстоянием 3, то есть способные исправить одну ошибку. Код Хемминга может быть представлен в таком виде, что синдром
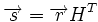
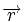
будет равен номеру позиции, в которой произошла ошибка. Это свойство позволяет сделать декодирование очень простым.
Код Рида-Малера
Код Рида-Малера [en:Reed-Muller code] — линейный код.
Общий метод кодирования линейных кодов
Линейный код длины n с k информационными символами является k-мерным линейным подпространством, поэтому каждое кодовое слово является линейной комбинацией базисных векторов 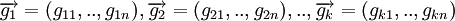
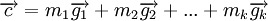
Либо с помощью порождающей матрицы:
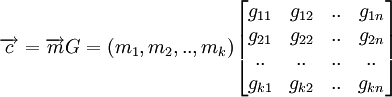
Это соотношение есть правило кодирование, по которому информационное слово 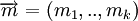
Общий метод обнаружения ошибок в линейном коде
Любой код (в том числе нелинейный) можно декодировать с помощью обычной таблицы, где каждому значению принятого слова 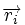
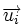
Для линейных кодов этот метод можно существенно упростить. При этом для каждого принятого вектора 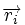
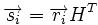
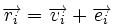
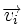
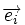
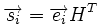
Линейные циклические коды
Несмотря на то, что исправление ошибок в линейных кодах уже значительно проще исправления в большинстве нелинейных, для большинства кодов этот процесс все ещё достаточно сложен. Циклические коды, кроме более простого декодирования, обладают и другими важными свойствами.
Циклическим кодом является линейный код, обладающий следующим свойством: если 
В дальнейшем, если не указано иное, мы будем считать, что циклический код является двоичным, то есть v0,v1 … могут принимать значения 0 или 1.
Порождающий полином
С помощью порождающего полинома осуществляется кодирование циклическим кодом. В частности:
Коды CRC
Таким образом, вид полинома g(x) задает конкретный код CRC. Примеры наиболее популярных полиномов:
| название кода | степень | полином |
|---|---|---|
| CRC-12 | 12 | x 12 + x 11 + x 3 + x 2 + x + 1 |
| CRC-16 | 16 | x 16 + x 15 + x 2 + 1 |
| CRC-x 16 + x 15 + x 5 + 1 | ||
| CRC-32 | 32 | x 32 + x 26 + x 23 + x 22 + x 16 + x 12 + x 11 + x 10 + x 8 + x 7 + x 5 + x 4 + x 2 + x + 1 |
Коды БЧХ
Коды Боуза-Чоудхури-Хоквингема (БЧХ) являются подклассом двоичных циклических кодов. Их отличительное свойство — возможность построения кода БЧХ с минимальным расстоянием не меньше заданного. Это важно, потому что, вообще говоря, определение минимального расстояния кода есть очень сложная задача.
Математически построение кодов БЧХ и их декодирование используют разложение порождающего полинома g(x) на множители в поле Галуа.
Коды Рида-Соломона
Коды Рида-Соломона (РС-коды) фактически являются недвоичными кодами БЧХ, то есть элементы кодового вектора являются не битами, а группами битов. Очень распространены коды Рида-Соломона, работающие с байтами (октетами).
Преимущества и недостатки линейных кодов
Хотя линейные коды, как правило, хорошо справляются с редкими, но большими пачками ошибок, их эффективность при частых, но небольших ошибках (например, в канале с АБГШ), менее высока. Благодаря линейности для запоминания или перечисления всех кодовых слов достаточно хранить в памяти кодера или декодера существенно меньшую их часть, а именно только те слова, которые образуют базис соответствующего линейного пространства. Это существенно упрощает реализацию устройств кодирования и декодирования и делает линейные коды весьма привлекательными с точки зрения практических приложений.
Оценка эффективности
Эффективность кодов определяется количеством ошибок, которые тот может исправить, количеством избыточной информации, добавление которой требуется, а также сложностью реализации кодирования и декодирования (как аппаратной, так и в виде программы для ЭВМ).
Граница Хемминга и совершенные коды
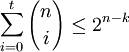
Коды, удовлетворяющие этой границе с равенством, называются совершенными. К совершенным кодам относятся, например, коды Хемминга. Часто применяемые на практике коды с большой корректирующей способностью (такие, как коды Рида-Соломона) не являются совершенными.
Энергетический выигрыш
При передаче информации по каналу связи вероятность ошибки зависит от отношения сигнал/шум на входе демодулятора, таким образом при постоянном уровне шума решающее значение имеет мощность передатчика. В системах спутниковой и мобильной, а также других типов связи остро стоит вопрос экономии энергии. Кроме того, в определенных системах связи (например, телефонной) неограниченно повышать мощность сигнала не дают технические ограничения.
Поскольку помехоустойчивое кодирование позволяет исправлять ошибки, при его применении мощность передатчика можно снизить, оставляя скорость передачи информации неизменной. Энергетический выигрыш определяется как разница отношений с/ш при наличии и отсутствии кодирования.
Применение
Линейные коды применяются:
Линейные коды применяются в сетевых протоколах различных уровней.