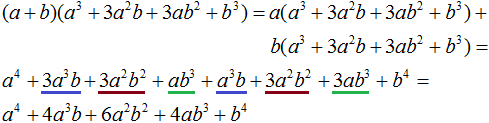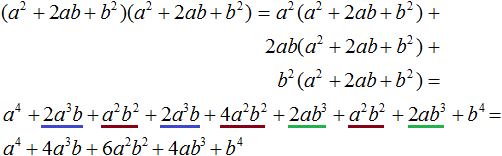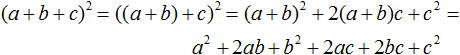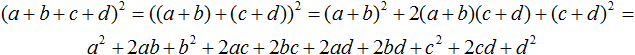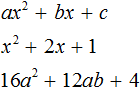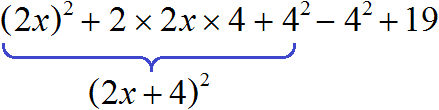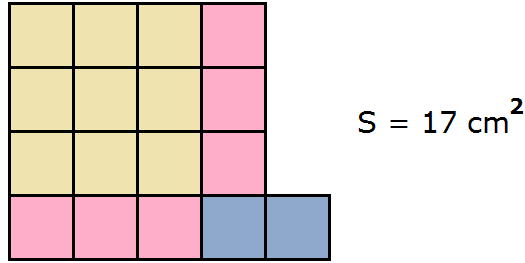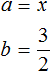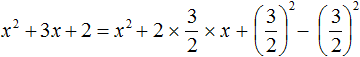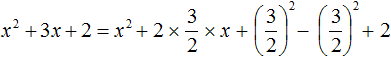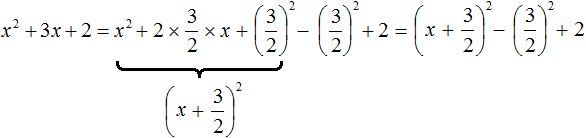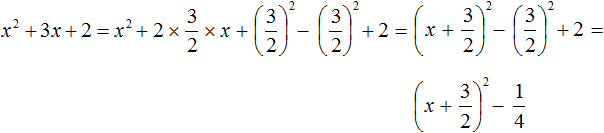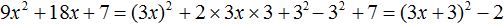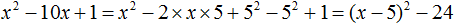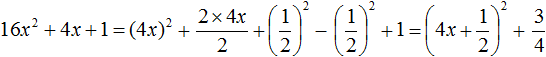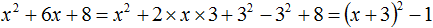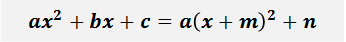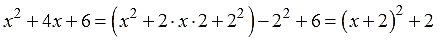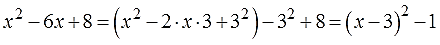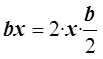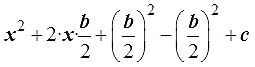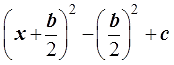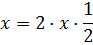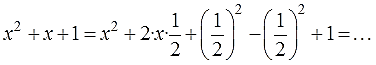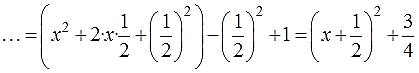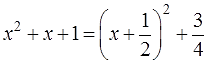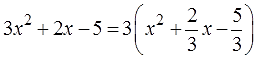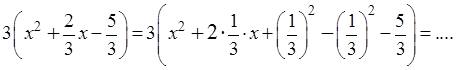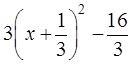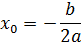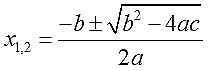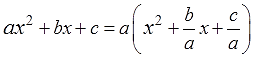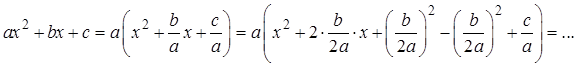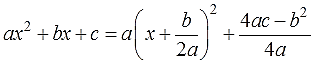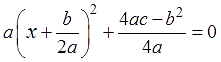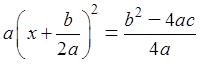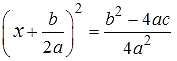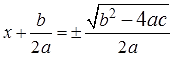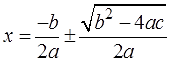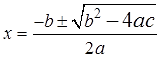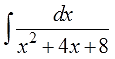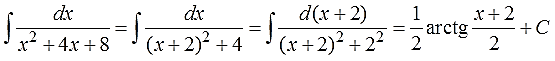Полный квадрат двучлена что это
Тождественные преобразования многочленов
Возведение двучлена в степень
Двучлен — это многочлен, состоящий из двух членов. В прошлых уроках мы возводили двучлен во вторую и третью степень, тем самым получили формулы сокращенного умножения:
Но двучлен можно возводить не только во вторую и третью степень, но и в четвёртую, пятую или более высокую степень.
К примеру, возведём двучлен a + b в четвертую степень:
Представим это выражение в виде произведения двучлена a + b и куба этого же двучлена
Сомножитель (a + b) 3 можно заменить на правую часть формулы куба суммы двух выражений. Тогда получим:
А это обычное перемножение многочленов. Выполним его:
То есть при возведении двучлена a + b в четвертую степень получается многочлен a 4 + 4a 3 b + 6a 2 b 2 + 4ab 3 + b 4
Возведение двучлена a + b в четвертую степень можно выполнить ещё и так: представить выражение (a + b) 4 в виде произведения степеней (a + b) 2 (a + b) 2
А это опять же обычное перемножение многочленов. Выполним его. У нас получится тот же результат, что и раньше:
Возведение трёхчлена в степень
Трёхчлен — это многочлен, состоящий из трёх членов. Например, выражение a + b + c является трёхчленом.
Иногда может возникнуть задача возвести трёхчлен в степень. Например, возведём в квадрат трехчлен a + b + c
Два члена внутри скобок можно заключить в скобки. К примеру, заключим сумму a + b в скобки:
В этом случае сумма a + b будет рассматриваться как один член. Тогда получается, что в квадрат мы возводим не трёхчлен, а двучлен. Сумма a + b будет первым членом, а член c — вторым членом. А как возводить в квадрат двучлен мы уже знаем. Для этого можно воспользоваться формулой квадрата суммы двух выражений:
Применим эту формулу к нашему примеру:
Таким же способом можно возвести в квадрат многочлен, состоящий из четырёх и более членов. Например, возведем в квадрат многочлен a + b + c + d
Теперь воспользуемся формулой квадрата суммы двух выражений:
Выделение полного квадрата из квадратного трёхчлена
Ещё одно тождественное преобразование, которое может пригодиться при решении задач это выделение полного квадрата из квадратного трёхчлена.
Квадратным трехчленом называют трёхчлен второй степени. Например, следующие трехчлены являются квадратными:
Итак, переменная a равна 2x
Отсюда делаем вывод, что переменная b равна 4
Значит, нашим полным квадратом будет выражение (2x) 2 + 2 × 2x × 4 + 4 2
Итак, возвратимся к исходному трехчлену 4x 2 + 16x + 19 и попробуем аккуратно внедрить в него полученный нами полный квадрат (2x) 2 + 2 × 2x × 4 + 4 2
Вместо 4x 2 записываем (2x) 2
Далее вместо 16x записываем удвоенное произведение, а именно 2 × 2x × 4
Далее прибавляем квадрат второго выражения:
А член 19 пока переписываем как есть:
4x 2 + 16x + 19 = (2x) 2 + 2 × 2x × 4 + 4 2 + 19
(2x) 2 + 2 × 2x × 4 + 4 2 + 19 = 4x 2 + 16x + 4 2 + 19
Чтобы сохранить значение исходного многочлена, нужно после прибавления члена 4 2 сразу же вычесть его
4x 2 + 16x + 19 = (2x) 2 + 2 × 2x × 4 + 4 2 − 4 2 + 19
4x 2 + 16x + 19 = (2x) 2 + 2 × 2x × 4 + 4 2 − 4 2 + 19 = (2x + 4) 2 − 4 2 + 19
4x 2 + 16x + 19 = (2x) 2 + 2 × 2x × 4 + 4 2 − 4 2 + 19 = (2x + 4) 2 − 4 2 + 19 = (2x + 4) 2 + 3
Значит, 4x 2 + 16x + 19 = (2x + 4) 2 + 3
Пример 2. Выделить полный квадрат из квадратного трёхчлена x 2 + 2x + 2
Следующий член исходного трёхчлена 2x перепишем в виде удвоенного произведение первого выражения (это у нас x ) и второго выражения b (это будет 1).
Теперь вернёмся к исходному квадратному трёхчлену и внедрим в него полный квадрата x 2 + 2x + 1 2
x 2 + 2x + 2 = x 2 + 2x + 1 2 − 1 2 + 2 = (x + 1) 2 + 1
Как и в прошлом примере член b (в данном примере это 1) после прибавления сразу был вычтен с целью сохранения значения исходного трёхчлена.
Рассмотрим следующее числовое выражение:
Значение этого выражения равно 17
Второй член 6 представим в виде удвоенного произведения первого члена 3 и второго 1
3 2 + 6 + 2 = 3 2 + 2 × 3 × 1 + 1 2 − 1 2 + 2
Свернем полный квадрат, а члены −1 2 и 2 слóжим:
3 2 + 6 + 2 = 3 2 + 2 × 3 × 1 + 1 2 − 1 2 + 2 = (3 + 1) 2 + 1
(3 + 1) 2 +1 = 4 2 + 1 = 17
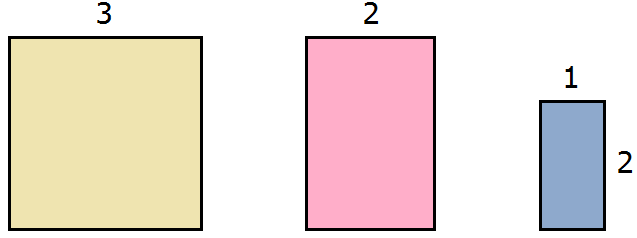
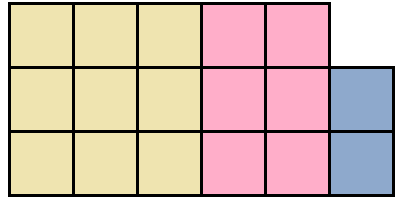
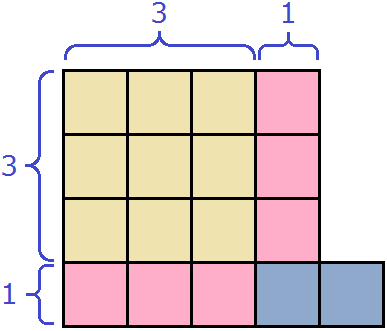
Допустим, у нас имеются квадрат и два прямоугольника. Квадрат со стороной 3 см, прямоугольник со сторонами 2 см и 3 см, а также прямоугольник со сторонами 1 см и 2 см
Запишем сумму площадей этих прямоугольников:
Это выражение можно понимать как объединение квадрата и двух прямоугольников в единую фигуру:
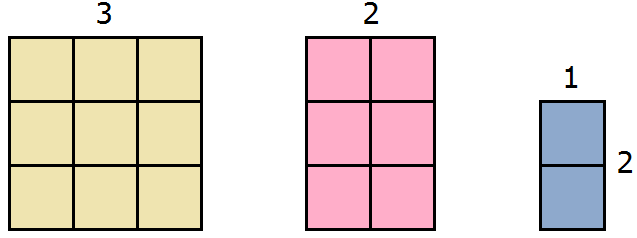
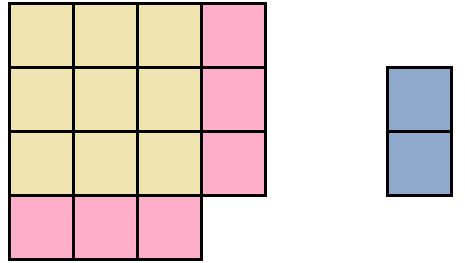
Попробуем из имеющейся фигуры образовать квадрат. Причем максимально большой квадрат. Для этого будем использовать части от розового и сиреневого прямоугольника.
Чтобы образовать максимально большой квадрат из имеющейся фигуры, можно желтый квадрат оставить без изменений, а половину от розового прямоугольника прикрепить к нижней части желтого квадрата:
Видим, что до образования полного квадрата не хватает еще одного квадратного сантиметра. Его мы можем взять от сиреневого прямоугольника. Итак, возьмем один квадрат от сиреневого прямоугольника и прикрепим его к образуемому большому квадрату:
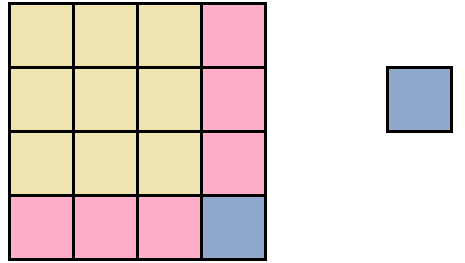
Теперь внимательно посмотрим к чему мы пришли. А именно на желтую часть фигуры и розовую часть, которая по сути увеличила прежний жёлтый квадрат. Не означает ли это то, что была сторона квадрата равная 3 см, и эта сторона была увеличена на 1 см, что привело в итоге к увеличению площади?
(3 + 1) 2
(3 + 1) 2 = 3 2 + 6 + 1 = 9 + 6 + 1 = 16
Действительно, в образовавшемся квадрате содержится 16 квадратов.
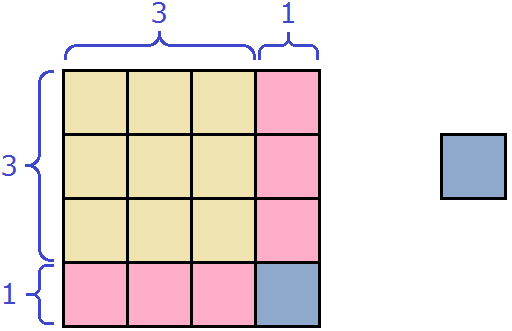
Оставшийся один квадратик от сиреневого прямоугольника можно прикрепить к образовавшемуся большому квадрату. Ведь речь изначально шла о единой фигуре:
(3 + 1) 2 + 1
9 + 6 + 2 = 3 2 + 6 + 2 = 3 2 + 2 × 3 × 1 + 1 2 − 1 2 + 2 = (3 + 1) 2 + 1
Пример 4. Выполним выделение полного квадрата из квадратного трёхчлена x 2 + 6x + 8
x 2 + 6x + 8 = x 2 + 2 × x × 3 + 3 2 − 3 2 + 8 = (x + 3) 2 − 1
Например, выполним выделение полного квадрата из квадратного трёхчлена x 2 + 3x + 2
Возвращаемся к нашему примеру и прибавляем квадрат второго выражения, и чтобы значение выражения не изменилось, сразу же вычитаем его:
Прибавляем оставшийся член 2
Свернём полный квадрат:
Оставшийся квадрат второго выражения и число 2 можно сложить. В итоге получим:
Пример 6. Выполним выделение полного квадрата из квадратного трёхчлена 9x 2 + 18x + 7
Пример 7. Выполним выделение полного квадрата из квадратного трёхчлена x 2 − 10x + 1
Пример 8. Выполним выделение полного квадрата из квадратного трёхчлена 16x 2 + 4x + 1
Пример 9. Разложить многочлен x 2 + 6x + 8 на множители при помощи выделения полного квадрата.
Сначала выделим полный квадрат:
Выделение полного квадрата двучлена из квадратного трёхчлена
Умение проделывать такую процедуру крайне необходимо во многих темах математики, связанных с квадратным трёхчленом ax 2 +bx+c. Самые распространённые:
2) Решение многих заданий на квадратный трёхчлен (квадратные уравнения и неравенства, задачи с параметрами и т.д.);
3) Работа с интегралами от некоторых функций, содержащих квадратный трёхчлен, а также работа с кривыми второго порядка (для студентов).
Полезная штука, короче! Претендуете на пятёрку? Тогда осваиваем!)
Что значит выделить полный квадрат двучлена в квадратном трёхчлене?
Это задание означает, что исходный квадратный трёхчлен c помощью тождественных преобразований выражений надо преобразовать вот к такому виду:
Число a что слева, что справа — одно и то же. Коэффициент при квадрате икса. Потому и обозначен одной буквой. Умножается справа на квадрат скобок. В самих скобках сидит тот самый двучлен, о котором и идёт речь в этой теме. Сумма чистого икса и какого-то числа m. Да, прошу обратить внимание, именно чистого икса! Это важно.
А вот буковки m и n справа — некоторые новые числа. Какие уж получатся в результате наших преобразований. Они могут получиться положительными, отрицательными, целыми, дробными — всякими! В примерах ниже сами увидите. Эти числа зависят от коэффициентов a, b и c. Для них есть свои специальные общие формулы. Достаточно громоздкие, с дробями. Поэтому давать их прямо здесь и сейчас я не буду. Зачем вашим светлым головам лишний мусор? Да и неинтересно это. Поработаем творчески.)
Что необходимо знать и понимать?
Прежде всего, необходимо знать назубок формулы сокращённого умножения. Хотя бы две из них — квадрат суммы и квадрат разности.
Без этой парочки формул — никуда. Не только в этом уроке, а почти во всей остальной математике вообще. Намёк понятен?)
Но одних лишь механически заученных формул здесь недостаточно. Нужно ещё грамотно уметь применять эти формулы. Причём не столько напрямую, слева направо, сколько наоборот, справа налево. Т.е. по исходному квадратному трёхчлену уметь расшифровывать квадрат суммы/разности. Это значит, вы должны легко, на автомате, узнавать равенства типа:
Без этого полезного навыка — тоже никак… Так что если с этими простыми вещами проблемы, то закрывайте эту страницу. Рановато вам сюда.) Сначала сходите по ссылочке выше. Она — для вас!
Ах, вы давно в теме? Отлично! Тогда читаем дальше.)
Как выделить полный квадрат двучлена в квадратном трёхчлене?
Начнём, разумеется, с простого.
Уровень 1. Коэффициент при x 2 равен 1
Это самая простая ситуация, требующая минимум дополнительных преобразований.
Например, дан квадратный трёхчлен:
Внешне выражение очень похоже на квадрат суммы. Мы знаем, что в квадрате суммы сидят чистые квадраты первого и второго выражений (a 2 и b 2 ), а также удвоенное произведение 2ab этих самых выражений.
Почти всё. Остаётся лишь добавить 6, в соответствии с исходным трёхчленом. Шестёрка-то никуда не делась! Пишем:
Скобки сути выражения не меняют, зато чётко подсказывают, что, как и почему. Осталось свернуть эти три слагаемых в полный квадрат по формуле, сосчитать в числах оставшийся хвостик -2 2 +6 (это будет 2) и записать:
Всё. Мы выделили квадрат скобок (x+2) 2 из исходного квадратного трёхчлена х 2 +4х+6. Превратили его в сумму полного квадрата двучлена (x+2) 2 и некоторого постоянного числа (двойки). А теперь я запишу всю цепочку наших преобразований в компактном виде. Для наглядности.
И все дела.) Вот и вся суть процедуры выделения полного квадрата.
Кстати, чему здесь равны числа m и n? Да. Каждое из них равно по двойке: m=2, n=2. Так уж получилось в ходе выделения.
Выделить полный квадрат двучлена:
И опять первый взгляд — на слагаемое с иксом. Превращаем 6х в удвоенное произведение икса и тройки. Перед удвоенным — минус. Значит, выделяем квадрат разности. Прибавляем (для получения полного квадрата) и тут же вычитаем (для компенсации) тройку в квадрате, т.е. 9. Ну и про восьмёрку не забываем. Получим:
Улавливаете принцип? Тогда настал черёд освоить и общий алгоритм. Всё то же самое, но через буквы. Итак, перед нами квадратный трёхчлен x 2 +bx+c (a=1). Что мы делаем:
1. Смотрим на слагаемое с иксом в первой степени ( bx) и превращаем его в удвоенное произведение икса на b/2:
2. К удвоенному произведению прибавляем и тут же отнимаем квадрат числа b/2. Прибавляем — для дополнения до полного квадрата. Отнимаем — для компенсации. В самом конце прибавляем свободный член с.
3. Первые три слагаемых сворачиваем в квадрат суммы/разности по соответствующей формуле. Оставшееся снаружи выражение аккуратно считаем в числах.
Ясненько? Первые два примера были совсем простые, с целыми числами. Для знакомства. Хуже, когда в процессе преобразований вылезают дроби. Главное здесь — не бояться! А чтобы не бояться, всяко надо знать действия с дробями, да…) Но здесь же пятёрочный уровень, не так ли? Усложняем задачу.
Допустим задан такой трёхчлен:
Как в этом трёхчлене организовать квадрат суммы? Не вопрос! Точно так же. Работаем по пунктам.
1. Смотрим на слагаемое с иксом в первой степени ( bx) и превращаем его в удвоенное произведение икса на b/2.
Наше слагаемое с иксом есть просто икс. И… что? Как нам одинокий икс превратить в удвоенное произведение? Да очень просто! Прямо по инструкции. Вот так:
Число b в исходном трёхчлене — единичка. Стало быть, b/2 получается дробным. Одна вторая. 1/2. Ну и ладно. Не маленькие уже.)
2. К удвоенному произведению прибавляем и тут же отнимаем квадрат числа b/2. Прибавляем — для дополнения до полного квадрата. Отнимаем — для компенсации. В самом конце прибавляем свободный член с.
3. Первые три слагаемых сворачиваем в квадрат суммы/разности по соответствующей формуле. Оставшееся снаружи выражение аккуратно считаем в числах.
Здесь m=1/2, а n=3/4. Дробные числа. Бывает. Такой уж трёхчлен попался…
Такая вот технология. Разобрались? Можно двигать на следующий уровень?)
Уровень 2. Коэффициент при x 2 не равен 1 — как быть?
Это более общий случай по сравнению со случаем а=1. Объём вычислений, разумеется, возрастает. Это огорчает, да… Зато общий ход решения в целом остаётся прежним. Просто к нему добавляется всего один новый шаг. Это радует.)
Пока рассмотрим безобидный случай, безо всяких дробей и прочих подводных камней. Например:
В серединке стоит минус. Значит, будем подгонять под квадрат разности. Но коэффициент при квадрате икса — двойка. А проще работать с единичкой. C чистым иксом. Что делать? А вынесем-ка эту двойку за скобки! Чтоб не мешала. Имеем право! Получим:
Вот так. Теперь трёхчлен в скобках — уже с чистым иксом в квадрате! Как того требует алгоритм уровня 1. И теперь уже можно работать с этим новым трёхчленом по старой отработанной схеме. Вот и действуем. Выпишем-ка его отдельно да преобразуем:
Полдела сделано. Осталось вставить полученное выражение внутрь скобок, да раскрыть их обратно. Получится:
Фиксируем в голове:
Если коэффициент при квадрате икса не равен единице, то выносим этот коэффициент за скобки. С оставшимся внутри скобок трёхчленом работаем по привычному алгоритму для a=1. Выделив в нём полный квадрат, вставляем результат на место, а внешние скобки раскрываем обратно.
А если коэффициенты b и с не делятся нацело на а? Это — самый общий и одновременно самый скверный случай. Тогда только дроби, да… Ничего не поделать. Например:
Всё аналогично, отправляем тройку за скобки, получаем:
К сожалению, ни двойка, ни пятёрка нацело на тройку не делятся, поэтому коэффициенты нового (приведённого) трёхчлена — дробные. Ну и ничего страшного. Работаем прямо с дробями: две трети икс превращаем в удвоенное произведение икса на одну треть, прибавляем квадрат одной трети (т.е. 1/9), отнимаем его, отнимаем 5/3…
Дорешайте, чего уж там. Должно в итоге получиться:
И ещё одни грабли. Многие ученики лихо расправляются с положительными целыми и даже дробными коэффициентами, но зависают на отрицательных. Например:
Итого, с учётом минуса:
Вот и всё. Что? Не знаете, как выносить минус за скобки? Ну, это вопрос к элементарной алгебре седьмого класса, не к квадратным трёхчленам…
Зачем нужно уметь выделять полный квадрат?
Например, такое задание:
Что делать будем? По точкам строить? Можно, конечно. Маленькими шажочками по длинной дороге. Довольно тупо и неинтересно…
Прежде всего, напоминаю, что при построении любой параболы мы всегда предъявляем ей стандартный набор вопросов. Их два. А именно:
1) Куда направлены ветви параболы?
2) В какой точке находится вершина?
С направлением ветвей всё ясно прямо из исходного выражения. Ветви будут направлены вниз, ибо коэффициент перед x 2 — отрицательный. Минус один. Минус перед квадратом икса всегда переворачивает параболу.
А вот с расположением вершины всё не так очевидно. Есть, конечно, общая формула вычисления её абсциссы через коэффициенты a и b.
Но далеко не каждый помнит эту формулку, ох не каждый… А 50% тех, кто всё-таки помнит, спотыкаются на ровном месте и косячат в банальной арифметике (обычно при подсчёте игрека). Обидно, правда?)
Сейчас вы научитесь искать координаты вершины любой параболы в уме за одну минуту! И икс и игрек. Одним махом и безо всяких формул. Как? С помощью выделения полного квадрата!
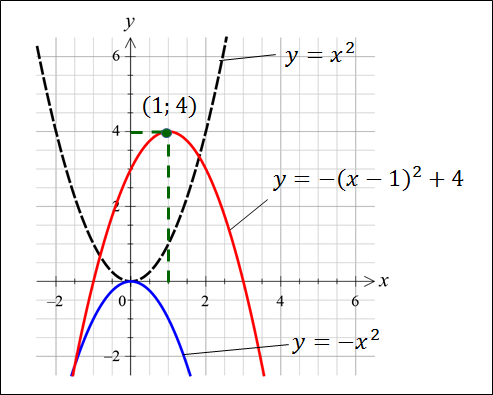
Итак, выделим полный квадрат в нашем выражении. Получим:
Кто хорошо прошарен в общих сведениях о функциях и хорошо освоил тему «преобразования графиков функций», тот без труда сообразит, что наша искомая парабола получается из обычной параболы y=x 2 c помощью трёх преобразований. Это:
1) Смена направления ветвей.
2) Параллельный перенос параболы у=- x 2 по иксу на 1 единицу ВПРАВО.
3) Параллельный перенос параболы y=-( x-1) 2 по игреку на 4 единицы ВВЕРХ.
Картинка будет следующей:
Собственно, именно по этой причине я с такой настойчивостью заострял ваше внимание на числах m и n, получающихся в процессе выделения полного квадрата. Не догадались, зачем? Да. Дело в том, что точка с координатами (-m; n) — это всегда вершина параболы y=a(x+m) 2 +n. Просто смотрим на числа в преобразованном трёхчлене и в уме даём верный ответ, где находится вершина. Удобно, правда?)
Рисование парабол — это первая полезная вещь. Переходим ко второй.
Полезная вещь вторая — решение квадратных уравнений и неравенств.
Да-да! Выделение полного квадрата во многих случаях оказывается гораздо быстрее и эффективнее традиционных приёмов решения подобных заданий. Сомневаетесь? Пожалуйста! Вот вам задание:
Узнали? Да! Это классическое квадратное неравенство. Все такие неравенства решаются по стандартному алгоритму. Для этого нам надо:
1) Сделать из неравенства уравнение стандартного вида и решить его, найти корни.
2) Нарисовать ось Х и отметить точками корни уравнения.
3) Схематично изобразить параболу по исходному выражению.
4) Определить области +/- на рисунке. Выбрать нужные области по исходному неравенству и записать ответ.
Собственно, весь этот процесс и напрягает, да…) И, более того, не всегда спасает от ошибок в нестандартных ситуациях типа этого примера. Попробуем сначала по шаблону?
Итак, выполняем пункт первый. Делаем из неравенства уравнение:
Стандартное квадратное уравнение, без фокусов. Решаем! Считаем дискриминант:
Вот-те раз! А дискриминант-то отрицательный! Нет корней у уравнения! И на оси рисовать нечего… Что делать?
Вот тут некоторые могут сделать вывод, что исходное неравенство тоже не имеет решений. Это фатальное заблуждение, да… Зато с помощью выделения полного квадрата верный ответ к этому неравенству можно дать за полминуты! Сомневаетесь? Что ж, можете засекать время.
Итак, выделяем полный квадрат в нашем выражении. Получаем:
Исходное неравенство стало выглядеть вот так:
А теперь, ничего далее не решая и не преобразовывая, просто включаем элементарную логику и соображаем: если к квадрату какого-то выражения (величине заведомо неотрицательной!) прибавить ещё единичку, то какое число мы в итоге получим? Да! Строго положительное!
А теперь смотрим на неравенство:
Переводим запись с математического языка на русский: при каких икс строго положительное выражение будет строго больше нуля? Не догадались? Да! При любых!
Вот вам и ответ: х — любое число.
А сейчас вернёмся к алгоритму. Всё-таки понимание сути и простое механическое заучивание — вещи разные.)
Суть алгоритма в том, что мы из левой части стандартного неравенства делаем параболу, и смотрим, где она выше оси Х, а где ниже. Т.е. где положительные значения левой части, где отрицательные.
Если мы сделаем из нашей левой части параболу:
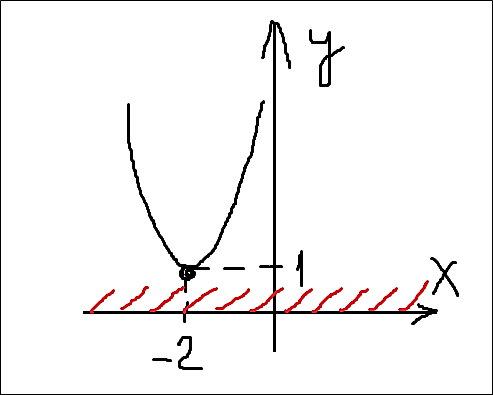
и нарисуем её график, то увидим, что вся парабола целиком проходит выше оси Х. Картинка будет выглядеть вот так:
Парабола кривовата, да… На то она и схематичная. Но при этом всё что нам надо, на картинке видно. Нет у параболы точек пересечения с осью Х, нет нулевых значений игрека. И отрицательных значений, естественно, тоже нет. Что и показано штриховкой всей оси Х целиком. Кстати, ось Y и координаты вершины я здесь изобразил не зря. Сравните координаты вершины параболы (-2; 1) и наше преобразованное выражение!
И как вам? Да! В нашем случае m=2 и n=1. Стало быть, вершина параболы имеет координаты: (-m; n) = (-2; 1). Всё логично.)
Простецкое квадратное уравнение. Можно решать по старинке, через дискриминант. Можно через теорему Виета. Как угодно. Математика не возражает.)
А если ни тот, ни другой способы того… не помним? Что ж, двойка вам светит, по-хорошему, но… Так уж и быть, спасу! Покажу, как можно решать некоторые квадратные уравнения только лишь методами седьмого класса. Снова выделяем полный квадрат!)
А теперь расписываем полученное выражение как… разность квадратов! Да-да, есть такая формула сокращённого умножения в седьмом классе:
Вставляем это разложение в уравнение вместо квадратного трёхчлена:
Осталось сообразить, что произведение множителей равно нулю тогда и только тогда, когда какой-нибудь из них равен нулю. Вот и приравниваем (в уме!) к нулю каждую скобку.
Вот и всё. Те же самые два корня. Такой вот искусный приёмчик. В дополнение к дискриминанту.)
К слову, о дискриминанте и об общей формуле корней квадратного уравнения:
Полезная вещь третья — вывод формулы корней квадратного уравнения.
Ну что, поехали! Берём квадратный трёхчлен в общем виде ax 2 +bx+c и… начинаем выделять полный квадрат! Да, прямо через буквы! Была арифметика, стала — алгебра.) Сначала, как обычно, выносим букву a за скобки, а все остальные коэффициенты делим на a:
Вот так. Это вполне законное преобразование: а не равно нулю, и делить на неё можно. А со скобками снова работаем по обычному алгоритму: из слагаемого с иксом делаем удвоенное произведение, прибавляем/отнимаем квадрат второго числа…
Всё то же самое, но с буквами.) Попробуйте доделать сами! Полезно!)
После всех преобразований у вас должно получиться вот что:
И зачем нам из безобидного трёхчлена сооружать такие нагромождения — спросите вы? Ничего, сейчас интересно будет! А теперь, знамо дело, приравниваем эту штуку к нулю:
Решаем как обычное уравнение, работаем по всем правилам, только с буквами. Делаем элементарные тождественные преобразования уравнений:
2) Очищаем квадрат скобок от коэффициента. Делим обе части на «а«. Слева, перед скобками, буква а исчезает, а справа уходит в знаменатель большой дроби, превращая его в 4a 2 .
Получается вот такое равенство:
У вас не так вышло? Тогда тема «Как выразить переменную из формулы?» — для вас. Срочно туда!
Следующим шагом извлекаем корень. Нас же икс интересует, верно? А икс под квадратом сидит… Извлекаем по правилам извлечения корней, разумеется. После извлечения получится вот это:
Слева квадрат суммы исчезает и остаётся просто сама эта сумма. Что и требуется.) А вот справа появляется плюс/минус. Ибо наша здоровенная дробь, несмотря на её устрашающий вид, это просто какое-то число. Дробное число. Зависящее от коэффициентов a, b, c. При этом корень из числителя этой дроби красиво не извлекается, там разность двух выражений. А вот корень из знаменателя 4a 2 вполне себе извлекается! Получится просто 2a.
Подумайте, почему знак модуля я всё-таки опустил. Очень полезно. Подсказка: ответ кроется в знаке плюс/минус перед дробью.)
Остались сущие пустяки. Обеспечиваем слева чистый икс. Для этого маленькую дробь переносим вправо. Со сменой знака, ясен перец. Напоминаю, что знак в дроби можно менять где угодно и как угодно. Хотим перед дробью поменяем, хотим в знаменателе, хотим в числителе. Я поменяю знак в числителе. Было +b, стало –b. Надеюсь, возражений нет?) После переноса станет так:
Складываем две дроби с одинаковыми знаменателями и получаем (наконец-то!):
Ну? Что тут сказать? Вау!)
Полезная вещь четвёртая — студентам на заметку!
А теперь плавненько переместимся из школы в ВУЗ. Вы не поверите, но выделение полного квадрата в высшей математике тоже нужно!
Например, такое задание:
Найти неопределённый интеграл:
С чего начинать? Прямое применение таблицы интегралов не катит. Только выделение полного квадрата и спасает, да…)
Кто не умеет выделять полный квадрат, тот навсегда зависнет на этом несложном примере. А кто умеет, тот выделяет и получает:
И теперь интеграл (для знающих) берётся одной левой!
Здорово, правда? И это не только интегралы! Я уж молчу про аналитическую геометрию, с её кривыми второго порядка — эллипсом, гиперболой, параболой и окружностью.
Определить тип кривой, заданной уравнением:
Без умения выделять полный квадрат задание не решить, да… А ведь пример проще некуда! Для тех, кто в теме, разумеется.
Группируем в кучки члены с иксом и с игреком и выделяем полные квадраты по каждой переменной. Получится:
Ну и как? Узнали, что за зверь?) Ну, конечно! Окружность радиуса тройка с центром в точке (3; 4).
И все дела.) Полезная штука — выделение полного квадрата!)