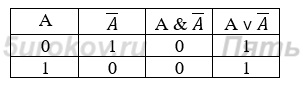
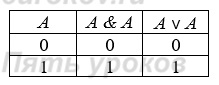
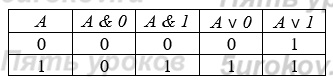
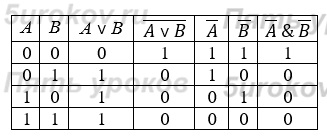
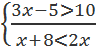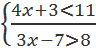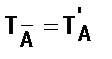Покажите что выполняя следующие задания мы находим множество истинности конъюнкции и дизъюнкции

Ответы по параграфу 1.4 Элементы алгебры логики

Задание 1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Дополняет ли презентация информацию, содержащуюся в тексте параграфа?

Задание 2. Объясните, почему следующие предложения не являются высказываниями.

Задание 3. Приведите по одному примеру истинных и ложных высказываний из биологии, географии, информатики, истории, математики, литературы.

• География:
1) Столица Италии – Париж. (ЛОЖЬ, т.к. это Рим, а Париж во Франции)
2) Выделяют 4 основные стороны света – север, юг, запад, восток.

• Информатика:
1) Инверсия – это логическое отрицание.
2) Конъюнкция – это логическое сложение. (ЛОЖЬ, т.к. это дизъюнкция является логическим сложением)

• История:
1) Промышленная революция (конец XVIII – первая половина XIX в.) началась в Англии в последней трети XVIII в.
2) Во времена аграрной революции в Англии в конце XVIII века землей владели фермеры, которые сдавали ее в аренду за определенную плату. (ЛОЖЬ, т.к. владели лендлорды, а фермеры были арендаторы)

• Математика:
1) У треугольника 5 сторон.
2) Квадрат гипотенузы равен сумме квадратов двух катетов.

• Литература:
1) Народные частушки – небольшие лирические песни, обычно имеющие форму четырехстрочного рифмованного куплета.
2) Первые упоминания о частушках относятся к 60-м годам XII века. (ЛОЖЬ, т.к это поздний жанр, появившийся только в XIX веке)

Задание 4. В следующих высказываниях выделите простые высказывания, обозначив каждое из них буквой; запишите с помощью букв и знаков логических операций каждое составное высказывание.

1) Число 376 чётное и трёхзначное.
А = Число 376 чётное
В = Число 376 трёхзначное
A & B

2) Зимой дети катаются на коньках или на лыжах.
A = Зимой дети катаются на коньках
B = Зимой дети катаются на лыжах
A | B

3) Новый год мы встретим на даче или на Красной площади.
A = Новый год мы встретим на даче.
B = Новый год мы встретим на Красной площади.
A | B

4) Неверно, что Солнце движется вокруг Земли.
A = Солнце движется вокруг Земли
¬A

5) Земля имеет форму шара, который из космоса кажется голубым.
A = Земля имеет форму шара, который из космоса кажется голубым.
B = Шар из космоса кажется голубым.
A & B

6) На уроке математики старшеклассники отвечали на вопросы учителя, а также писали самостоятельную работу.
A = На уроке математики старшеклассники отвечали на вопросы учителя
B = На уроке математики старшеклассники писали самостоятельную работу
A & B

Задание 5. Постройте отрицания следующих высказываний.

Задание 6. Пусть А = «Ане нравятся уроки математики», а В = «Ане нравятся уроки химии». Выразите следующие формулы на обычном языке:

Задание 7. Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот её фрагмент:

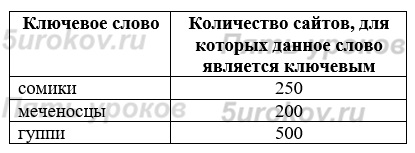
Дано дополнительно помимо таблицы:
сомики & гуппи – 0 сайтов;
сомики & меченосцы – 20 сайтов;
меченосцы & гуппи – 10 сайтов.

Нарисуем круги Эйлера:

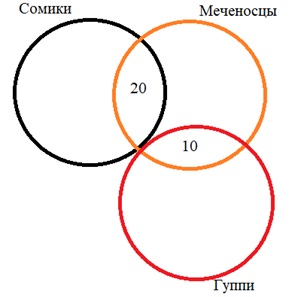
Чтобы найти количество сайтов, соответствующих этому запросу, к количеству элементов множества сомики (250) добавим количество элементов множества меченосцы без сомиков (200 – 20), а также гуппи без меченосцев (500 – 10).
Получаем: 250 + 180 + 490 = 920 сайтов
Ответ: 920 сайтов

2) Найти:
Для скольких сайтов рассматриваемого сегмента ложно высказывание «Сомики — ключевое слово сайта ИЛИ меченосцы — ключевое слово сайта ИЛИ гуппи — ключевое слово сайта»?
То есть это по сути всё, что не вошло в наш С | М | Г, то есть надо найти ¬(С | M | Г).
С | M | Г = 920
По условию задачи сегмент сети Интернет состоит из 1000 сайтов.
То есть, то, что не вошло в нашу область это 1000 – 920 = 80 сайтов.
Ответ: 80 сайтов

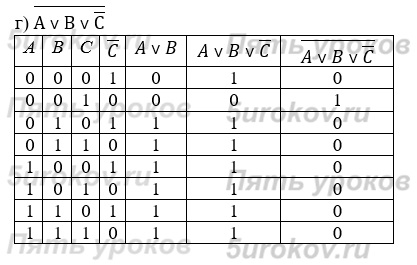
Задание 8. Постройте таблицы истинности для следующих логических выражений:

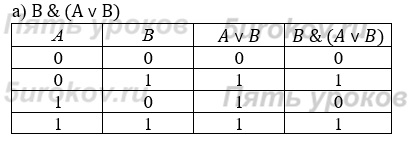
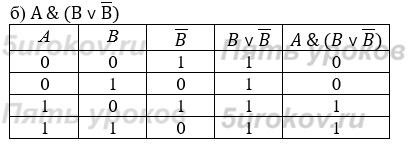
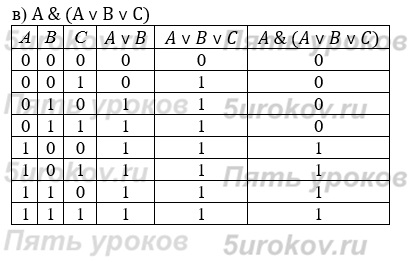
Задание 9. Проведите доказательство рассмотренных в параграфе логических законов с помощью таблиц истинности.

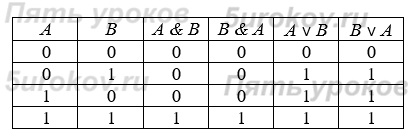
1) Переместительный (коммутативный) закон:

2) Сочетательный (ассоциативный закон):
для логического умножения:

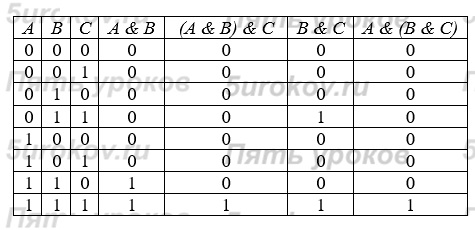
для логического сложения:

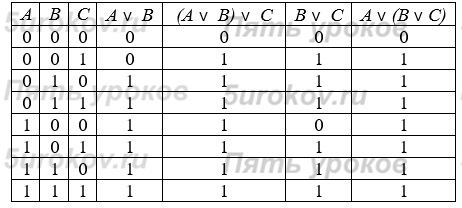
3) Распределительный (дистрибутивный) закон:

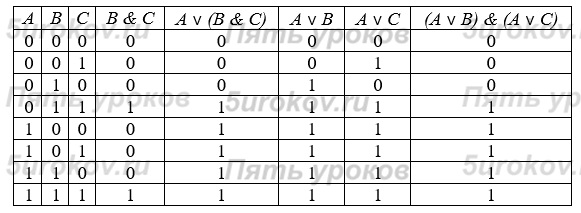
Совпадение значений в столбцах, соответствующих логическим выражениям в левой и правой частях равенства, доказывает справедливость распределительного закона для логического сложения.

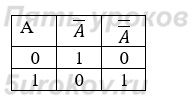
4) Закон двойного отрицания:

5) Закон исключенного третьего:

6) Закон повторения:

7) Закон операций с 0 и 1:

8) Законы общей инверсии:
а) для логического умножения:

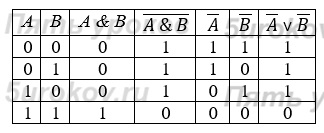
б) для логического сложения:

Задание 10. Даны три числа в десятичной системе счисления: A=23, B=19, C=26. Переведите A, B и C в двоичную систему счисления и выполните поразрядной логические операции (A ˅ B) & C. Ответ дайте в десятичной системе счисления.

Задание 11. Найдите значения выражений:

Задание 12. Найдите значение логического выражения для указанных значений числа Х:
а) 1; б) 2; в) 3; г) 4.

Задание 13. Пусть А = «Первая буква имени – гласная», В = «Четвертая буква имени согласная». Найдите значение логического выражения для следующих имён:

Задание 14. Разбирается дело Джона, Брауна и Смита. Известно, что один из них нашёл и утаил клад. На следствии каждый из подозреваемых сделал два заявления:
Смит: «Я не делал этого. Браун сделал это.»
Джон: «Браун не виновен. Смит сделал это.»
Браун: «Я не делал этого. Джон не делал этого.»
Суд установил, что один из них дважды солгал, другой дважды сказал правду, третий один раз солгал, один раз сказал правду. Кто из подозреваемых должен быть оправдан?

Задание 15. Алеша, Боря и Гриша нашли в земле старинный сосуд. Рассматривая удивительную находку, каждый высказал по два предположения. Где и в каком веке изготовлен сосуд?

Только в 1 прав, в другом не прав, следовательно, иcходя из 2 логических принципов составляем уравнение:
• 0 v 1 = 1
• 1 & 1=1
Усл. Обозначения:
Г – греческий, Ф – Финикийский, Цифра – век

(Г или 5)&(Ф или 3)&(неГ или 4)=1

Распределительный закон, раскрываем скобки:
(ГФ или Г3 или Ф5 или 53) & (неГ или 4)=1
ГФ и 53 обнуляем, т.к. это ложь (0), не может быть одновременно и то, и другое правдой. С тем, что осталось еще раз распределительный закон, раскрываем скобки:
(Г3 и неГ) или Г34 или (Ф5 и неГ) или Ф54 = 1
Г и неГ не может быть одновременно, обнуляем
Г34 обнуляем, Ф54 обнуляем.
Остается:
Ф5 и неГ = 1

Ответ: Финикийский сосуд, изготовлен в V веке.

Источник

МАТЕМАТИЧЕСКИЕ ПРЕДЛОЖЕНИЯ

Изучая реальные процессы, математика описывает их, используя как естественный словесный язык, так и свой символический. Описание строится при помощи предложений. Но чтобы математические знания были достоверными, правильно отражали окружающую нас реальность, эти предложения должны быть истинными.

Но как узнать, истинное или ложное знание заключено в том или ином математическом предложении? На этот и другие вопросы, с ним связанные, отвечает раздел «математические предложения». А сейчас только заметим, что каждое математическое предложение характеризуется содержанием и логической формулой (структурой), причем содержание неразрывно связано с формой, и нельзя осмыслить первое, не понимая второго. В связи с этим изучение математических предложений будет в основном связано с раскрытием логической структуры математических предложений.

ТЕМА. ВЫСКАЗЫВАНИЯ И ВЫСКАЗЫВАТЕЛЬНЫЕ ФОРМЫ (ЛЕКЦИЯ)

1. Высказывания и высказывательные формы

2. Конъюнкция и дизъюнкция высказываний

3. Конъюнкция и дизъюнкция высказывательных форм

ПРАКТИЧЕСКАЯ РАБОТА. ВЫСКАЗЫВАНИЯ И ВЫСКАЗЫВАТЕЛЬНЫЕ ФОРМЫ

Цель. Рассмотреть общие подходы к изучению математических предложений в начальном курсе математики, уметь раскрыть их логическую структуру. Рассмотреть правила определения значения истинности составного высказывания и нахождение множества истинности составных высказывательных форм.

Теоретическая часть

Вопросы к изучению

1. Высказывания и высказывательные формы

2. Конъюнкция и дизъюнкция высказываний

3. Конъюнкция и дизъюнкция высказывательных форм

Основные понятия темы

Ø значение истинности высказывания;

Ø высказывательная форма;

Ø область определения высказывательной формы;

Ø множество истинности высказывательной формы;

Ø элементарные высказывания;

Ø логические связки;

Ø составные высказывания;

Ø конъюнкция высказываний и высказывательных форм;

Ø дизъюнкция высказываний и высказывательных форм.

Правила

Ø определения значения истинности составного высказывания;

Ø нахождения множества истинности составных высказывательных форм: Т _{А Ù В} = Т_А Ç Т _В, Т _{А Ú В} = Т_А È Т _В, Т 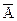= Т’_А;

Обозначения

А Ù В – составное высказывание, читают «А и В»;

А Ú В – составное высказывание, читают «А или В»

Практическая часть

2. Какие предложения из упражнения 1 являются высказывательными формами? Подставьте в них значение переменной так, чтобы получилось: а) истинное высказывание; б) ложное высказывание.

3. Можно ли считать высказывательными формами следующие записи: а) х 2 – 2х; б) 7×4+2=30; в) 4х +2у; г) 7×4 +2 2; б) 2

7. Какова логическая структура (форма) следующих предложений: а) Средняя линия треугольника параллельна основанию и равна его половине; б) Если число делится на 2 и на 3, то оно делится на 6; в) Треугольник АВС не является равносторонним.

8. Приведите примеры математических предложений, имеющих логическую структуру вида: а) А и В; б) А или В; в) если А, то В.

10. Известно, что высказывание А истинно. Можно ли, зная лишь это, определить значение истинности высказывания: а) А Ú В; б) А Ù В?

11. Известно, что высказывание А – ложно. Можно ли, зная лишь это, определить значение истинности высказывания: а) А Ú В; б) А Ù В?

12. Определите значение истинности каждого высказывания: а) число 6 делится на 2 и на 3; б) число 123 делится на 3 и на 9; в) при делении 42 на 5 в остатке получится 2 или 5;Г) 3£7; ж) 3³7.

13. Каждое из следующих предложений замените конъюнкцией либо дизъюнкцией, имеющей тот же смысл: а) число 7 принадлежит хотя бы одному из множеств А и В; б) квадратное уравнение имеет не более двух корней; в) каждое слагаемое суммы х+у+z делится на 3; г) по крайней мере одно из натуральных чисел n, n-1, n+1 четно.

14. Покажите, что, выполняя следующие задания, мы находим множество истинности конъюнкции и дизъюнкции высказывательных форм:

а) Даны числа: 31,53,409,348,20,3094,233,33,271,143,3,333,14,30. Выпишите все числа, в записи которых: 1) три цифры и есть цифра 3; 2) три цифры или есть цифра 3.

б) Из ряда 25, 12, 17, 5, 15, 36 выпишите те числа, которые: 1) делятся на 3 и 9; 2) делятся на 3 или на 9.

15. Выполните следующие задания и дайте обоснование предложенным ответам:

а) Постройте по два треугольника, принадлежащих множеству А, если оно состоит из: 1) прямоугольных и равнобедренных треугольников; 2) прямоугольных или равнобедренных треугольников.

б) Постройте два четырехугольника, у которых: 1) диагонали равны и есть прямой угол; 2) диагонали равны или есть прямой угол.

в) Запишите три числа, которые: 1) делятся на 4 и больше 12; 2) делятся на 4 или 12.

16. Решите следующие системы неравенств и объясните, что представляет собой любая система неравенств и множество ее решений с точки зрения логики:

а) б)

17. Решите уравнение (х-3)×(х+2) ×(х-7)=0, х ÎR. Использовалось ли вами понятие дизъюнкции высказывательных форм?

18. Вместо многоточия вставьте «и» либо «или»: а) х ÎAÇB тогда и только тогда, когда х ÎA …х ÎВ. б) х ÎAÈB тогда и только тогда, когда х ÎA …х ÎВ.

20. Пусть А – множество ромбов, В – множество прямоугольников. Как называется четырехугольник, являющийся одновременно ромбом и прямоугольником? Как можно выразить множество К таких четырехугольников через множества А и В?

1. А – множество четных натуральных чисел, В – множество натуральных чисел, меньших 20. Установите, какие из следующих высказываний истинны:

а) 5ÎA или 5ÎB; д) 44 Î А или 44 ÎВ;

б) 5 Î А и 5 Î В; е) 44 Î А и 44 Î В;

в) 8 Î А или 8 Î В; ж) 51 Î А или 51 ÎВ;

г) 8 ÎА и 8 ÎВ; з) 51 Î А и 51 Î В.

2. Покажите, что выполнение учащимися начальных классов следующих заданий связано с понятием высказывательной формы, области ее определения и множества истинности: а) Из ряда чисел 1, 2, 3, 4, 5, 6, 7, 8, 9 выпишите, которые делятся на 3; б) Назови все числа, меньшие 7 (имеются в виду только целые неотрицательные числа).

3. Что можно сказать об истинности высказываний: «если а ÎМ, то а Ï », «если а делится на 3 и в не делится на 3, то а + в не делится на 3». Назовите простые высказывания, входящие в каждое из приведенных.

4. Являются ли высказываниями следующие записи: «3–2», «3

Источник

Конъюнкция и дизъюнкция высказывательных форм

В математике рассматривают не только конъюнкцию и дизъюнкцию высказываний, но и выполняют соответствующие операции над высказывательными формами.

Конъюнкцию одноместных высказывательных форм А(х) и В(х), заданных на множестве Х, обозначают А(х) Ù В(х). С появлением этого предложения возникает вопрос, как найти его множество истинности, зная множества истинности высказывательных форм А(х) и В (х). Другими словами, при каких значениях х из области определения Х высказывательная форма А(х)ÙВ(х) обращается в истинное высказывание? Очевидно, что это возможно при тех и только тех значениях х, при которых обращаются в истинное высказывание обе высказывательные формы А(х) и В(х). Если обозначить Т_А – множество истинности предложения А(х), Т_В – множество истинности предложения В(х), а множество истинности их конъюнкции Т_А˄В, то, по всей видимости, Т_А˄В = Т_А Т_В.

Докажем это равенство.

2. Докажем обратное утверждение. Пусть а – произвольный элемент множества Х и известно, что а ∈ Т_А Т_В. По определению пересечения множеств это означает, что а ∈ Т_А и а ∈ Т_В, откуда получаем, что А(х) и В(х) – истинные высказывания, поэтому конъюнкция высказываний А(х)˄В(х) также будет истинна. А это означает, что элемент а принадлежит множеству истинности высказывательной формы А(х)˄В(х), т.е. а ∈ Т_А˄В. Таким образом, мы доказали, что Т_А Т_В ∈ Т_А˄В.

Из 1 и 2 в силу определения равных множеств вытекает справедливость равенства Т_А˄В = Т_А Т_В, что и требовалось доказать.

Заметим, что полученное правило справедливо и для высказывательных форм, содержащих более одной переменной.

Приведем примериспользования этого правила. Найдем множество истинности конъюнкции двух неравенств 2х > 10 и 4+х 10 ˄ 4+х 10, а Т₂ – множество решений неравенства 4+х

Рассматривая конъюнкцию и дизъюнкцию высказывательных форм, мы установили их тесную связь с пересечением и объединением множеств.

С другой стороны, характеристические свойства элементов пересечения и объединения множеств А и В представляют собой соответственно конъюнкцию и дизъюнкцию характеристических свойств данных множеств:

А B = <х½х∈A ˄ х∈B>, А B = <х½х∈A ˄ х∈B>, причем каждое свойство представляет собой высказывательную форму.

Упражнения

1. Покажите, что, выполняя следующие задания, мы находим множество истинности конъюнкции и дизъюнкции высказывательных форм:

а) Даны числа: 31,53,409,348,20,3094,233,33,271,143,3,333,14,30.

Выпишите все числа, в записи которых:

1) три цифры и есть цифра 3;

2) три цифры или есть цифра 3.

б) Из ряда 25, 12, 17, 5, 15, 36 выпишите те числа, которые:

1) двузначные или меньше 17;

2) двузначные и меньше 17.

в) Из ряда 72,312,522,483,1137 выпишите те числа, которые:

1) делятся на 3 и 9;

2) делятся на 3 или на 9.

2. Выполните следующие задания и дайте обоснование предложенным ответам:

а) Постройте по два треугольника, принадлежащих множеству А, если оно состоит из:

1) прямоугольных и равнобедренных треугольников;

2) прямоугольных или равнобедренных треугольников.

б) Постройте два четырехугольника, у которых:

1) диагонали равны и есть прямой угол;

2) диагонали равны или есть прямой угол.

в) Запишите три числа, которые:

1) делятся на 4 и больше 12;

2) делятся на 4 или 12.

3. Решите следующие системы неравенств и объясните, что представляет собой любая система неравенств и множество ее решений с точки зрения логики:

а)

б)

4. Решите уравнение (х-3)×(х+2) ×(х-7)=0, х ∈ R. Использовалось ли вами понятие дизъюнкции высказывательных форм?

5. Вместо многоточия вставьте «и» либо «или»:

а) х ∈ A B тогда и только тогда, когда х ∈ A …х ∈ В.

б) х ∈ A B тогда и только тогда, когда х ∈ A …х ∈ В.

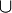
6. Пусть А – множество ромбов, В – множество прямоугольников. Как называется четырехугольник, являющийся одновременно ромбом и прямоугольником? Как можно выразить множество К таких четырехугольников через множества А и В?

Источник

ПРАКТИЧЕСКАЯ РАБОТА. ВЫСКАЗЫВАНИЯ И ВЫСКАЗЫВАТЕЛЬНЫЕ ФОРМЫ

Цель. Рассмотреть общие подходы к изучению математических предложений в начальном курсе математики, уметь раскрыть их логическую структуру. Рассмотреть правила определения значения истинности составного высказывания и нахождение множества истинности составных высказывательных форм.

Теоретическая часть

Вопросы к изучению

1. Высказывания и высказывательные формы.

2. Конъюнкция и дизъюнкция высказываний.

3. Конъюнкция и дизъюнкция высказывательных форм.

Основные понятия темы

Ø значение истинности высказывания;

Ø высказывательная форма;

Ø область определения высказывательной формы;

Ø множество истинности высказывательной формы;

Ø элементарные высказывания;

Ø логические связки;

Ø составные высказывания;

Ø конъюнкция высказываний и высказывательных форм;

Ø дизъюнкция высказываний и высказывательных форм.

Правила

Ø определения значения истинности составного высказывания;

Ø нахождения множества истинности составных высказывательных форм: Т _{А Ù В} = Т_А Ç Т _В, Т _{А Ú В} = Т_А È Т _В,

Обозначения

А Ù В – составное высказывание, читают «А и В»;

А Ú В – составное высказывание, читают «А или В»

Практическая часть

1. Среди следующих предложений, рассматриваемых в начальном курсе математики, укажите высказывания и определите их значение истинности: а) (12-7)×(6+3)=45; б) (15+12) : 3>10; в) в любом прямоугольнике противоположные стороны равны; г) (12 – х) × 4 =24; д) среди четырехугольников есть такие, у которых все стороны равны; е) число z – двузначное; ж) произведение чисел 4070 и 8 меньше, чем сумма чисел 18396 и 14174; з) число 6 является корнем уравнения (12 – х) × 4=24.

2. Какие предложения из упражнения 1 являются высказывательными формами? Подставьте в них значение переменной так, чтобы получилось: а) истинное высказывание; б) ложное высказывание.

3. Можно ли считать высказывательными формами следующие записи: а) х 2 – 2х; б) 7×4+2=30; в) 4х +2у; г) 7×4 +2 2; б) 2

Источник

Информатика. 10 класс

Конспект урока

Информатика, 10 класс. Урок № 11.

Тема — Алгебра логики. Таблицы истинности

Перечень вопросов, рассматриваемых в теме: высказывание, логическая переменная, логические операции (отрицание, конъюнкция, дизъюнкция, строгая дизъюнкция, импликация, эквиваленция), логические выражения, предикаты и их множества истинности, таблицы истинности и их анализ.

Глоссарий по теме: импликация, эквиваленция, предикат, примеры законов алгебры логики.

Основная литература по теме урока:

Л. Л. Босова, А. Ю. Босова. Информатика. Базовый уровень: учебник для 10 класса

— М.: БИНОМ. Лаборатория знаний, 2017 (с.174—197)

Открытые электронные ресурсы по теме:

Теоретический материал для самостоятельного изучения:

Алгебра логики — раздел математики, изучающий высказывания, рассматриваемые с точки зрения их логических значений (истинности или ложности), и логические операции над ними.

Алгебра логики возникла в середине XIX века в трудах английского математика Джорджа Буля. Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами. В 1938 году Клод Шеннон применил алгебру логики для описания процесса функционирования релейно-контактных и электронно-ламповых схем. Логическое высказывание — это повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.

Например, предложение «Джордж Буль — основоположник алгебры логики» истинно, а «Солнце — спутник Земли» ложно.

Употребляемые в обычной речи логические связки «не», «и», «или», «если…то», «тогда и только тогда» и др. позволяют из уже заданных высказываний строить новые высказывания. Высказывания, образованные из других высказываний, называются составными. Высказывание, никакая часть которого не является высказыванием, называется элементарным. Например, из двух простых высказываний (каких?) можно получить следующее составное высказывание: «Алгебра логики является основой строения логических схем компьютеров и служит математической основой решения сложных логических задач». Истинность или ложность составных высказываний зависит от истинности или ложности образующих их высказываний и определённой трактовки связок (логических операций над высказываниями).

Обоснование истинности или ложности элементарных высказываний не является задачей алгебры логики. Эти вопросы решаются теми науками, к сфере которых относятся элементарные высказывания. Такое сужение интересов позволяет обозначать высказывания символическими именами (например, А, В, С).

Логическая переменная — это переменная, которая обозначает любое высказывание и может принимать логические значения «истина» или «ложь». Для логических значений «истина» — «ложь» могут использоваться следующие обозначения: И — Л, true — false, да — нет, 1 — 0.

Логическая операция полностью может быть описана таблицей истинности, указывающей, какие значения принимает составное высказывание при всех возможных значениях образующих его элементарных высказываний.

В алгебре логики имеется шесть логических операций. Из курса информатики 8—9 классов вам знакомы три из них:

— отрицание (инверсия, логическое НЕ)

Высказыванию ставится в соответствие новое высказывание, значение которого противоположно исходному.

— конъюнкция (логическое умножение, логическое И)

Высказывание истинно тогда и только тогда, когда истинны оба исходных высказывания.

— дизъюнкция (логическое сложение, логическое ИЛИ)

Высказывание ложно тогда и только тогда, когда ложны оба исходных высказывания.

Рассмотрим новые логические операции.

— Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся ложным тогда и только тогда, когда первое высказывание (посылка) истинно, а второе (следствие) — ложно, называется импликацией (от лат. implicatio — сплетение, тесная связь) или логическим следованием.

Операция импликации обозначается символом и задается следующей таблицей истинности:

В разговорной речи импликации соответствуют предложения, содержащие связку «если…, то». Как правило, эту связку мы используем, когда хотим показать зависимость одного события от другого.

Импликацию можно заменить на выражение, использующее ранее изученные операции НЕ и ИЛИ:

— Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным тогда и только тогда, когда только одно из двух высказываний истинно, называется строгой (исключающей) дизъюнкцией.

Строгая дизъюнкция обозначается символоми задается следующей таблицей истинности:

В русском языке строгой дизъюнкции соответствует связка «либо». Например, в пословице «Либо пан, либо пропал», выполнение обоих условий одновременно невозможно. В отличие от обычной дизъюнкции в высказывании, содержащем строгую дизъюнкцию, мы утверждаем, что произойдет только одно событие.

Строгую дизъюнкцию можно представить через базовые операции следующим образом:

Чтобы доказать это равенство, достаточно для всех возможных комбинаций и вычислить значения выражения, стоящего в правой части равенства, и сравнить их со значениями выражения для тех же исходных данных.

— Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным, когда оба исходных высказывания истинны или оба исходных высказывания ложны, называется эквиваленцией или равнозначностью.

В логике эквиваленция обозначается символом и задается следующей таблицей истинности:

В разговорной речи эквивалентности соответствует связка «тогда и только тогда, когда», а в математике — «необходимо и достаточно».

Если посмотреть внимательно на таблицы истинности для двух последних логических операций, то можно заметить, что эквивалентность — это обратная операция для операции «исключающее ИЛИ», т. е.

Можно заменить эквивалентность выражением, которое включает только базовые логические операции:

Составное логическое высказывание можно представить в виде логического выражения (формулы), состоящего из логических констант (0, 1), логических переменных, знаков логических операций и скобок.

Для логического выражения справедливо:

При преобразовании или вычислении значения логического выражения логические операции выполняются в соответствии с их приоритетом:

Операции одного приоритета выполняются в порядке их следования, слева направо. Как в математике, скобки меняют порядок выполнения операций.

Дан фрагмент таблицы истинности выражения F.

Источник