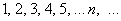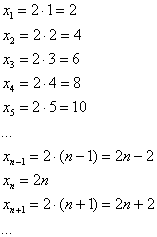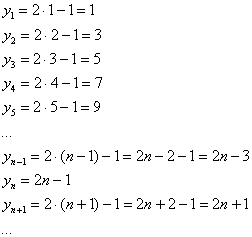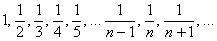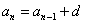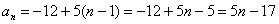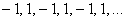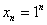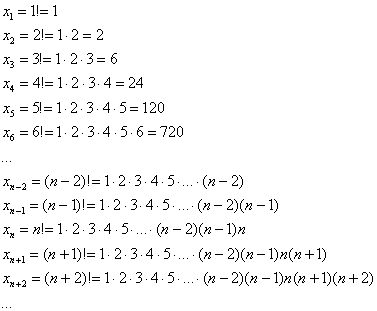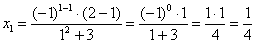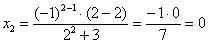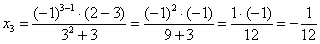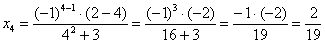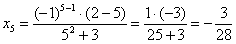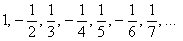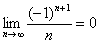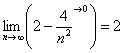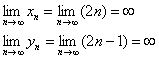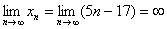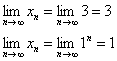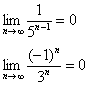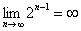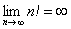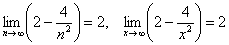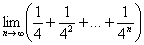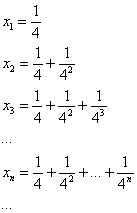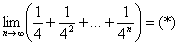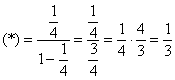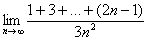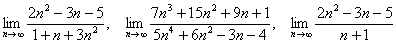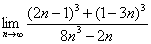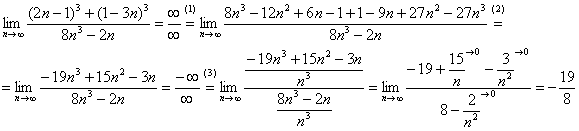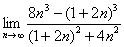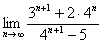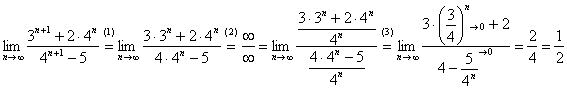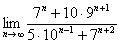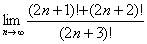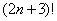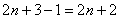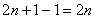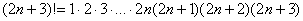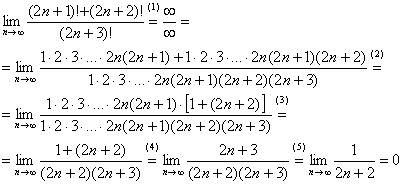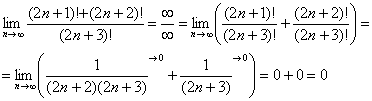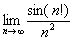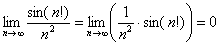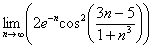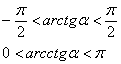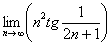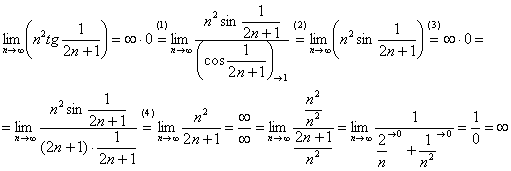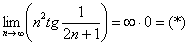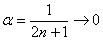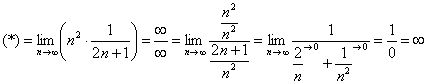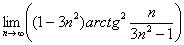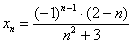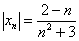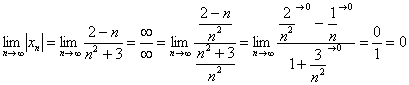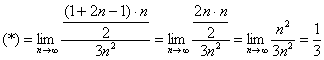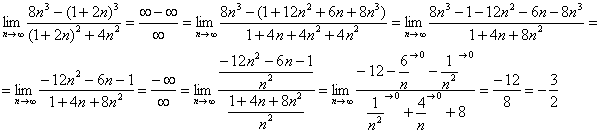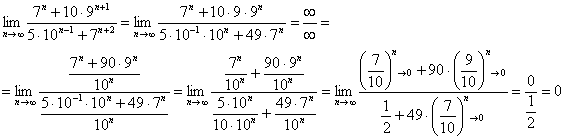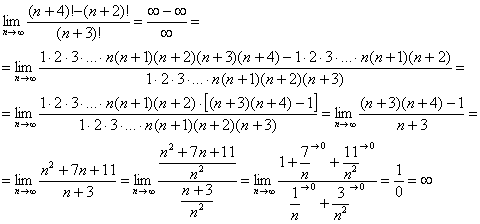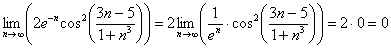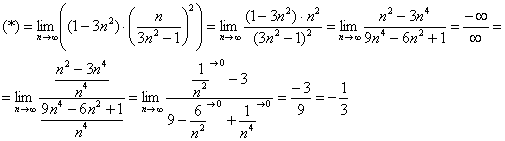Показать по определению что lim an a вычислить n
Показать по определению что lim an a вычислить n
`|x_n-a| oo) x_n=a` (читается: предел `x_n` при `n`, стремящемся к бесконечности, равен `a`). Последовательность, называется сходящейся, если существует число `a`, являющееся её пределом. Если такого числа `a` не существует, то последовательность называется расходящейся.
Часто в определении предела полагают число `k` натуральным. Однако, как нетрудно понять, получится эквивалентное определение.
Пусть выбрано произвольное `epsilon>0`. Нам нужно найти такое число `k`, что при всех `n>k` выполнялось бы неравенство `|x_n-c| k` имеет место неравенство `|x_n-c| oo)x_n=c`.
В разобранном примере число `k` удалось выбрать так, чтобы оно годилось сразу для всех `epsilon`. Такой случай не типичен.
Доказать, что `lim_(n->oo)1/n=0`.
Могут ли два разных числа быть пределами одной и той же последовательности?
Пусть `lim_(n->oo)x_n=a`. Имеет ли предел последовательность `(x_(n+1))`?
Пусть `lim_(n->oo)x_n=a`, `epsilon>o`. Можно ли утверждать, что найдётся такое число `k`, что `|x_n-a| k`?
Да. Поскольку `lim_(n->oo)x_n=a`, то по определению предела для любого положительного числа `alpha`, а следовательно, и для `alpha=epsilon//2`, найдётся число `k`, такое что `|x_n-a|k`.
Сформулируем необходимое условие существования предела.
Если последовательность имеет предел, то она ограничена.
Доказать, что последовательность `x_n=(-1)^n` не имеет предела.
Предположим противное, т. е. какое-то число `a` является пределом этой последовательности. Тогда для `epsilon=1` найдётся такое число `k`, что `|x_n-a| k`. Пусть номер `N>k`, тогда `|x_N-a| oo)y_n!=0`). При этом
Ограничимся доказательством пункта 2. Фиксируем произвольное `epsilon>0`. Нам нужно показать, что существует такое число `k`, что `|x_ny_n-ab| k`. По теореме 2.1 последовательности `(x_n)` и `(y_n)` ограничены; тем самым найдётся такое `C>0`, что `|x_n| k_1`, а также число `k_2` такое, что `|y_n-b| k_2`. Если положить `k=max
`|x_ny_n-ab| oo)cx_n=clim_(n->oo)x_n` для любого `cinR`.
В самом деле, рассмотрим последовательность `y_n=c`. Поскольку `lim_(n->oo)y_n=c` (пример 2.1), то по пункту 2 теоремы 2.2
Показать, что `lim_(n->oo) 1/(n^2)=0`.
Поскольку `lim_(n->oo) 1/n=0`, то по пункту 2 теоремы 2.2
`lim_(n->oo) 1/(n^2)=lim_(n->oo) 1/n*lim_(n->oo) 1/n=0`.
Теорему 2.2 можно обобщить на произвольное (конечное) число слагаемых (сомножителей). В частности, `lim_(n->oo)1/n^m=0` для любого `m inN`.
Обозначим дробь, стоящую под знаком предела, через `x_n`. В числителе и знаменателе `x_n` стоят последовательности, не являющиеся ограниченными (доказывается аналогично примеру 1.6). По теореме 2.1 они не имеют предела и теорема о пределе частного (теорема 2.2 3)) «напрямую» здесь неприменима. Поступим следующим образом: поделим числитель и знаменатель на наибольшую степень `n`. По формулам сокращённого умножения `(n+2)^3-n(n-1)^2=8n^2+11n+8`, так что `x_n` можно переписать в виде:
Теперь в числителе и знаменателе `x_n` стоят сходящиеся последовательности:
По пункту 3 теоремы 2.2
Следующее полезное свойство пределов известно под названием теоремы о «зажатой» последовательности.
Для данного `epsilon>0` существует такое число `k_1`, что члены `x_n` лежат в интервале `(a-epsilon, a+epsilon)` при всех `n>k_1`, и существует такое число `k_2`, что члены `z_n` лежат в интервале `a-epsilon;a+epsilon)` при всех `n>k_2`. Положим `k=max
Попробуем «зажать» `x_n` между членами последовательностей, сходящихся к одному и тому же числу, и применим теорему 2.3.
`sqrt(n^2+n) 1/(n+1) iff n/(sqrt(n^2+n))>n/(n+1)`.
Учитывая `n/(sqrt(n^2+1)) oo)n/(n+1)=1` и `lim_(n->oo)1=1`, по теореме 2.3 `lim_(n->oo)x_n=1`.
Если для любого `n inN`, `n>=n_0` выполняется неравенство `a_n oo)a_n=a`, `lim_(n->oo)b_n=b`, то `a b`. По определению предела для `epsilon=(a-b)/2` найдутся такие `k_1`, `k_2`, что для `n>k_1` выполняется `|a_n-a| k_2` выполняется `|b_n-b| k` имеем `b_n oo)1/n=0`.
В теории пределов важную роль играет следующий факт.
Всякая монотонная ограниченная последовательность имеет предел.
Эта теорема эквивалентна свойству полноты множества действительных чисел. Образно говоря, свойство полноты означает, что числовая ось является «сплошным» множеством, множеством без «дырок».
Предел последовательности
п.1. Определение последовательности
С понятием «последовательность» мы уже познакомились, когда изучали прогрессии (см. §24 справочника для 9 класса). По определению:
Т.е., числовая последовательность – это некий набор чисел с присвоенными им порядковыми номерами. Это набор можно задать формулой, описанием или просто перечислением.
Например:
1) Формула \(y_n=\frac1n,\ n\in\mathbb
2) Формула \(y_n=(-1)^n,\ n\in\mathbb
3) Рекуррентная формула \(y_1=1,\ y_2=1,\ y_(n+2)=y_(n+1)+y_n\) задает бесконечную последовательность чисел Фибоначчи:
4) Описание «число π точностью до \(10^<-n>\)» задает бесконечную последовательность все более «подробных» значений числа π:
Этот ряд можно также задать формулой \(y_n=\frac<[\pi\cdot 10^n]><10^n>\), где квадратные скобки обозначают целую часть от числа.
п.2. Предел последовательности
Поведение последовательности «на длинных дистанциях» может быть неочевидным. Чтобы лучше понять, возрастает или убывает заданный ряд чисел, ограничен ли он какой-либо величиной или уходит на бесконечность, проще всего построить график.
1) \(y_n=\frac1n\) Последовательность сходится к 0 |
2) \(y_n=(-1)^n\) Последовательность ни к чему не сходится |
3) числа Фибоначчи \(y_1=1,\ y_2=1,\ y_ Последовательность уходит на бесконечность |
4) приближения числа π Последовательность сходится к π |
п.3. Как доказать сходимость последовательности к пределу?
| \(\varepsilon\) | 0,1 | 0,01 | 0,001 | 0,0001 | 0,00001 | 0,000001 |
| \(N_<\varepsilon>\) | 7 | 97 | 997 | 9997 | 99997 | 999997 |
| \(\lg \varepsilon\) | -1 | -2 | -3 | -4 | -5 | -6 |
| \(\lg N_<\varepsilon>\) | 0,845 | 1,987 | 2,999 | 4,000 | 5,000 | 6,000 |
И построим график (в логарифмическом масштабе):
Мы видим, что чем меньше ε, тем больше \(N_<\varepsilon>\). Но главное – мы всегда можем его указать.
Таким образом, мы доказали, что действительно \(\lim_
Ведь для любого сколь угодно малого \(\varepsilon\gt 0\) мы можем указать такой номер \(N_<\varepsilon>=\left[\frac1\varepsilon-4\right]+1\), начиная с которого, для всех членов последовательности с номерами \(n\geq N_<\varepsilon>\) разность \(\left|\frac<1>
Построенный график интересен еще и тем, что показывает одно из важных практических применений логарифмов: если разбросы по шкалам очень велики, отличаются на порядки, то графики удобней строить в десятичных логарифмах.
Такие графики часто можно увидеть у физиков-ядерщиков, копающих вглубь, от нанометров до планковских длин; или у астрономов, всматривающихся вдаль, от тысяч километров до гигапарсек.
п.4. Ограниченные и неограниченные последовательности
п.5. Как доказать неограниченность последовательности?
Таким образом, мы доказали, что действительно \(\lim_
Ведь для любого сколь угодно большого \(M\gt 0\) мы можем указать такой номер \(N_M=[\sqrt
п.6. Примеры
| ε | 0,1 | 0,01 | 0,001 | 0,0001 | 0,00001 | 0,000001 |
| \(N_<\varepsilon>\) | 15 | 128 | 1253 | 12503 | 125003 | 1250003 |
Таким образом, для любого сколь угодно малого ε>0 найдется номер в последовательности \(N_<\varepsilon>=\left[\frac12\left(\frac<5><2\varepsilon>+3\right)\right]+1\), начиная с которого
\(\left|\frac
Что и требовалось доказать.
Показанный приём с усилением неравенства часто применяется в математическом анализе. Найденное \(N_<\varepsilon>\) немного больше «точного» значения, которое следует из исходной дроби \(\frac
Если найденный номер будет немного больше исходного – не страшно; главное, чтобы он 1) был обоснован; 2) гарантировал размещение всех последующих \(y_n,\ n\geq N_<\varepsilon>\) в ε окрестности предела b.
Таким образом, для любого сколь угодно малого ε>0 найдется номер в последовательности \(N_<\varepsilon>=\left[\frac<1><3\sqrt<\varepsilon>>\right]\), начиная с которого \(\left|\frac
Что и требовалось доказать.
Таким образом, для любого сколь угодно малого ε>0 найдется номер в последовательности \(N_<\varepsilon>=\left[-\log_3\varepsilon\right]\), начиная с которого \(\left|\frac<3^n+1><3^n>-1\right|\lt\varepsilon,\ n\geq N_<\varepsilon>\).
Что и требовалось доказать.
| ε | 0,1 | 0,01 | 0,001 | 0,0001 | 0,00001 | 0,000001 |
| \(N_<\varepsilon>\) | 2 | 362 | 39602 | 3996002 | 4·10 8 | 4·10 10 |
Таким образом, для любого сколь угодно малого ε>0 найдется номер в последовательности \(N_<\varepsilon>=\left[\left(\frac<1><5\varepsilon>-1\right)^2\right]\), начиная с которого \(\left|\frac<\sqrt
Что и требовалось доказать.
Пример 2. Используя определения неограниченной последовательности, докажите, что:
a) \( \lim_
По условию: \(y_n=2^n\)
Записываем неравенство \(|y_n|\gt M\):
\begin
Таким образом, для любого сколь угодно большого \(M\gt 0\) мы можем указать такой номер \(N_M=\left[\log_2M\right]+1\), начиная с которого, для всех членов последовательности с номерами \(n\geq N_M,\ y_n=2^n\gt M\).
Что и требовалось доказать.
| M | 10 | 100 | 1 000 | 10 000 | 100 000 | 1 000 000 |
| NM | 100 | 10 000 | 1 000 000 | 10 8 | 10 10 | 10 12 |
Таким образом, для любого сколь угодно большого \(M\gt 0\) мы можем указать такой номер \(N_M=\left[M^2\right]\), начиная с которого, для всех членов последовательности с номерами \(n\geq N_M,\ y_n=\sqrt
Что и требовалось доказать.
Числовая последовательность.
Как найти предел последовательности?
На данном уроке мы узнаем много интересного из жизни участников большого сообщества под названием Вконтакте числовые последовательности. Рассматриваемая тема относится не только к курсу математического анализа, но и затрагивает основы дискретной математики. Кроме того, материал потребуется для освоения других разделов вышки, в частности, в ходе изучения числовых рядов и функциональных рядов. Можно банально сказать, что это важно, можно ободряюще сказать, что это просто, можно сказать ещё много дежурных фраз, однако сегодня первая, необыкновенно ленивая учебная неделя, поэтому меня жутко ломает сочинять первый абзац =) Уже в сердцАх сохранил файл и собрался спать, как вдруг… голову озарила идея чистосердечного признания, которое невероятно облегчило душу и подтолкнуло к дальнейшему стуку пальцами по клавиатуре.
Отвлечёмся от летних воспоминаний, и заглянем в этот увлекательный и позитивный мир новой социальной сети:
Понятие числовой последовательности
Сначала задумаемся над самим словом: а что такое последовательность? Последовательность – это когда что-то расположено за чем-то. Например, последовательность действий, последовательность времён года. Или когда кто-то расположен за кем-то. Например, последовательность людей в очереди, последовательность слонов на тропе к водопою.
Немедленно проясним характерные признаки последовательности. Во-первых, члены последовательности располагаются строго в определённом порядке. Так, если двух человек в очереди поменять местами, то это уже будет другая последовательность. Во-вторых, каждому члену последовательности можно присвоить порядковый номер:
С числами всё аналогично. Пусть каждому натуральному значению 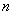
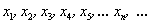
Да, в математических задачах в отличие от жизненных ситуаций последовательность почти всегда содержит бесконечно много чисел.
При этом:
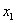
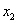
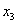
…
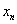
…
На практике последовательность обычно задаётся формулой общего члена, например:
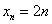
Таким образом, запись 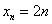
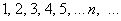
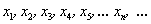
Последовательность положительных нечётных чисел 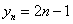
Ещё одна распространённая последовательность 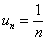
Как, наверное, многие подметили, переменная «эн» играет роль своеобразного счётчика.
На самом деле с числовыми последовательностями мы имели дело ещё в средних классах школы. Вспомним арифметическую прогрессию. Определение переписывать не буду, коснёмся самой сути на конкретном примере. Пусть 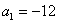
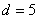
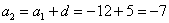
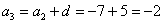
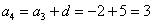
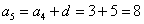
…
И, очевидно, энный член задаётся рекуррентной формулой
Примечание: в рекуррентной формуле каждый следующий член выражается через предыдущий член или даже через целое множество предыдущих членов.
Полученная формула малопригодна на практике – чтобы добраться, скажем, до 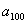
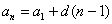
Подставьте в формулу 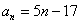
Аналогичные выкладки можно провести для геометрической прогрессии, энный член которой задаётся формулой 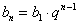
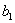
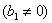
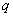
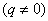
прогрессия 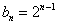
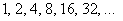
прогрессия 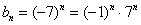
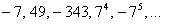
прогрессия 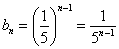
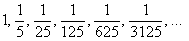
прогрессия 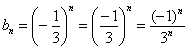
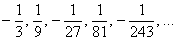
Надеюсь, все знают, что –1 в нечётной степени равно –1, а в чётной – единице.
Прогрессию называют бесконечно убывающей, если 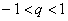
Давайте добавим в свой список двух новых друзей, один из которых только что постучался в матрицу монитора:
Последовательность 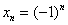
Таким образом, члены последовательности могут повторяться. Так, в рассмотренном примере последовательность состоит из двух бесконечно чередующихся чисел.
А бывает ли так, что последовательность состоит из одинаковых чисел? Конечно. Например, 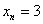
Факториал: 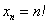
Всего лишь свёрнутая запись произведения:
Отнюдь не графомания, пригодится для задач 😉 Рекомендую осмыслить-запомнить и даже переписать в тетрадь. …Пришёл тут в голову один вопрос: а почему никто не создаёт такие полезные граффити? Едет себе человек в поезде, смотрит в окно и изучает факториалы. Панки отдыхают =)
Возможно, некоторым читателям всё-таки ещё не до конца понятно, как расписать члены последовательности, зная общий член. Тот редкий случай, когда контрольный выстрел возвращает к жизни:
Разберёмся с последовательностью 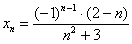
Сначала подставим в энный член значение 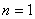
Далее подставим в общий член 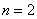
Потом подставим следующий номер 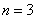
Четвёрку:
Чего уж, теперь и отличную отметку не зазорно заработать:
и так далее… пока разогреется самый последний чайник!
Понятие предела последовательности. Простейшие примеры
Для лучшего осмысления нижеследующей информации желательно ПОНИМАТЬ, что такое предел функции. Конечно, в стандартном курсе математического анализа сначала рассматривают предел последовательности и только потом предел функции, но дело в том, что о самой сущности предела я уже подробно рассказывал. Более того, в теории числовая последовательность считается частным случаем функции, и людям, которые знакомы с пределом функции, будет заметно веселее.
Впрочем, дальше могут читать все-все-все, однако если у вас возникнет непонимание или недопонимание чего-либо, то, пожалуйста, начните с пределов функций.
Пригласим на танец незамысловатую подругу 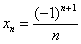
Что происходит, когда «эн» увеличивается до бесконечности? Очевидно, что члены последовательности будут бесконечно близко приближаться к нулю. Это и есть предел данной последовательности, который записывается следующим образом:
Если предел последовательности равен нулю, то её называют бесконечно малой.
В теории математического анализа даётся строгое определение предела последовательности через так называемую эпсилон-окрестность. Этому определению будет посвящёна следующая статья, а пока что разберём его смысл:
Изобразим на числовой прямой члены последовательности 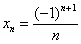
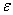
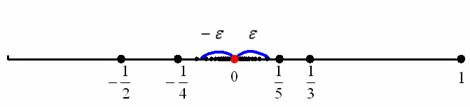
Теперь зажмите синюю окрестность рёбрами ладоней и начинайте её уменьшать, стягивая к пределу (красной точке). Число 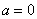
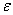
Последовательность 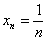
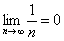
Естественно, предел может быть равен и любому другому конечному числу, элементарный пример:
Здесь дробь стремится к нулю, и соответственно, предел равен «двойке».
Если у последовательности 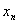
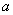
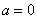
Последовательности 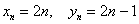
Арифметическая прогрессия с первым членом 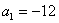
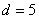
К слову, расходится и любая арифметическая прогрессия, за исключением случая с нулевым шагом – когда к конкретному числу 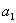
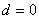
У последовательностей 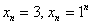
Любая бесконечно убывающая геометрическая прогрессия, как ясно уже из названия, бесконечно малА:
Если знаменатель геометрической прогрессии 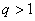
Если же 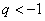
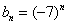
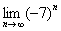
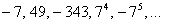
После небольшого разоблачения 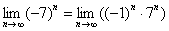
Действительно, для последовательности 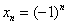
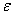
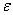
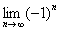
Факториал 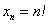
Причём, растёт он как на дрожжах, так, 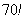
С контрольным выстрелом всё чуть сложнее, и мы как раз подошли к практической части лекции, в которой разберём боевые примеры:
Как найти предел последовательности?
А вот сейчас необходимо уметь решать пределы функций, как минимум, на уровне двух базовых уроков: Пределы. Примеры решений и Замечательные пределы. Потому что многие методы решения будут похожи. Но, прежде всего, проанализируем принципиальные отличия предела последовательности от предела функции:
В пределе последовательности «динамическая» переменная «эн» может стремиться только к «плюс бесконечности» – в сторону увеличения натуральных номеров 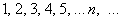
В пределе функции «икс» может быть направлен куда угодно – к «плюс/минус бесконечности» либо к произвольному действительному числу.
Последовательность дискретна (прерывна), то есть состоит из отдельных изолированных членов. Раз, два, три, четыре, пять, вышел зайчик погулять. Для аргумента же функции характерна непрерывность, то есть «икс» плавно, без приключений стремится к тому или иному значению. И, соответственно, значения функции будут так же непрерывно приближаться к своему пределу.
По причине дискретности в пределах последовательностей встречаются свои фирменные вещи, такие как факториалы, «мигалки», прогрессии и т.п. И сейчас я постараюсь разобрать пределы, которые свойственны именно для последовательностей.
Начнём с прогрессий:
Найти предел последовательности
Решение: нечто похожее на бесконечно убывающую геометрическую прогрессию, но она ли это? Для ясности распишем несколько первых членов:
Так как 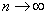
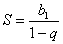
Используем формулу суммы бесконечно убывающей геометрической прогрессии: 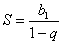
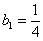
Главное, совладать с четырёхэтажностью дроби:
Написать первые четыре члена последовательности и найти её предел
Это пример для самостоятельного решения. Для устранения неопределённости 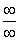
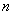
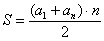
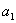
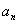
Поскольку в пределах последовательностей «эн» всегда стремится к «плюс бесконечности», то неудивительно, что неопределённость 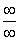
И многие примеры решаются точно так же, как пределы функций!
Как вычислить эти пределы? Смотрите Примеры № 1-3 урока Пределы. Примеры решений.
А может быть что-нибудь посложнее наподобие 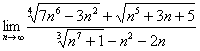
С формальной точки зрения разница будет лишь в одной букве – там «икс», а здесь «эн».
Приём тот же – числитель и знаменатель надо разделить на «эн» в старшей степени.
Также в пределах последовательностей достаточно распространена неопределённость 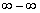
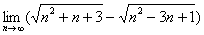
Чтобы разобраться с пределом 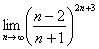
Следующие четыре примера (№ 3-6) тоже «двулики», но на практике почему-то больше характерны для пределов последовательностей, чем для пределов функций:
Найти предел последовательности
Решение: сначала полное решение, потом пошаговые комментарии:
(1) В числителе дважды используем формулу 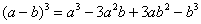
(2) Приводим подобные слагаемые в числителе.
(3) Для устранения неопределённости делим числитель и знаменатель на 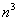
Как видите, ничего сложного.
Найти предел последовательности
Это пример для самостоятельного решения, формулы сокращенного умножения в помощь.
В пределах с показательными последовательностями применяется похожий метод деления числителя и знаменателя:
Найти предел последовательности
Решение оформим по той же схеме:
(1) Используя свойства степеней, вынесем из показателей всё лишнее, оставив там только «эн».
(2) Смотрим, какие показательные последовательности есть в пределе: 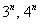
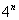
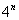
(3) В числителе и знаменателе проводим почленное деление. Поскольку 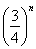
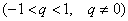
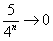
Найти предел последовательности
Это пример для самостоятельного решения.
Как-то незаслуженно остался в забвении стильный почерк, присущий только пределу последовательности. Пора исправить ситуацию:
Найти предел последовательности
Решение: чтобы избавиться от «вечного соперника» 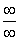
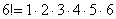
Последним множителем в произведении идёт шестёрка. Что нужно сделать, чтобы получить предыдущий множитель? Вычесть единицу: 6 – 1 = 5. Чтобы получить множитель, который располагается ещё дальше, нужно из пятёрки ещё раз вычесть единичку: 5 – 1 = 4. И так далее.
Не беспокойтесь, это не урок в первом классе коррекционной школы, на самом деле мы знакомимся с важным и универсальным алгоритмом под названием «как разложить любой факториал». Давайте разделаемся с самым злостным флудером нашего чата:
Очевидно, что последним множителем в произведении будет 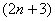
Как получить предыдущий множитель? Вычесть единицу:
Как достать прадедушку? Ещё раз вычесть единицу: 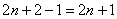
Ну и ещё на один шаг продвинемся вглубь:
Таким образом, наше чудовище распишется следующим образом:
С факториалами числителя всё проще, так, мелкие хулиганы.
Оформляем решение:
(1) Расписываем факториалы
(2) В числителе ДВА слагаемых. Выносим за скобки всё, что можно вынести, в данном случае это произведение 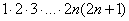
(3) Сокращаем числитель и знаменатель на 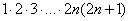
(4) Упрощаем числитель
(5) Сокращаем числитель и знаменатель на 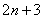
Более подготовленные студенты, которые легко раскладывают факториалы в уме, могут решить пример значительно быстрее. На первом шаге делим почленно числитель на знаменатель и мысленно выполняем сокращения:
Но способ с разложением всё-таки более основателен и надёжен.
Найти предел последовательности
Это пример для самостоятельного решения.
Желающие набить руку на рассмотренных типах пределов могут обратиться к сборнику Кузнецова. Около 150 прорешанных примеров можно найти здесь >>> (задачи № 2-6).
Как и в любом обществе, среди числовых последовательностей попадаются экстравагантные личности.
Теорема: произведение ограниченной последовательности на бесконечно малую последовательность – есть бесконечно малая последовательность.
Если вам не очень понятен термин «ограниченность», пожалуйста, изучите статью об элементарных функциях и графиках.
Аналогичная теорема справедлива, кстати, и для функций: произведение ограниченной функции на бесконечно малую функцию – есть бесконечно малая функция.
Найти предел последовательности
Решение: последовательность 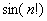
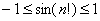
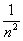
Просто и со вкусом. Да-да, так и оформляем.
Найти предел последовательности
Это пример для самостоятельного решения.
Ещё две распространённые ограниченные функции – арктангенс и арккотангенс:
Аргументы перечисленных тригонометрических функций могут быть заполнены знатной абракадаброй, но это не должно приводить в панику – существенно то, что последовательности ограничены!
Иногда в ходе вычисления пределов последовательностей приходится использовать довольно неожиданные приёмы:
Найти предел последовательности
Решение: неопределённость 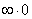
(1) Используем формулу 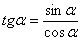
(2) Избавляемся от косинуса, указывая, что он стремится к единице.
(3) Неопределённость 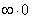
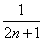
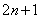
(4) Используем первый замечательный предел 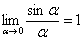
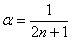
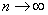
Прокатывает и 2-й метод решения – через замечательные эквивалентности:
Заменим бесконечно малую последовательность эквивалентной:
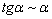
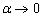
В данном случае
Найти предел последовательности
Это пример для самостоятельного решения. Здесь аргумент арктангенса также бесконечно мал, поскольку его знаменатель более высокого порядка роста, чем числитель. Решать, разумеется, значительно выгоднее через замечательную эквивалентность.
Оба рассмотренных примера справедливы и для функций, похожие пределы также разобраны в Примерах 12-13 урока о бесконечно малых величинах.
В заключение урока рассмотрим ещё один важный вопрос:
Как найти предел знакочередующейся последовательности?
Такая последовательность уже неоднократно встречалась в статье, например, первая скрипка теоретического параграфа 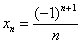
Действительно, как аналитически найти предел знакочередующейся последовательности, если знак то «плюс», то «минус»?
И я, наконец-то, заряжаю в свой револьвер тот самый волшебный патрон:
Найти предел последовательности
Решение: на первом шаге следует найти предел последовательности 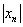
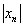
Теперь как ни в чём не бывало, вымучиваем наш обычный предел:
Получено конечное число. Очевидно, что знакочередование не поменяет сути – члены последовательности будут «прыгать» вокруг своего предела, бесконечно близко приближаясь к нему. Собственно, это проиллюстрировано на единственном рисунке данного урока.
Ситуация принципиально такая же, как, например, у более простых последовательностей 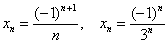
Ответ: так как последовательность является знакочередующейся и 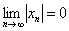
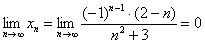
Если в ходе исследования знакочередующейся последовательности 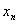
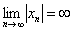
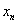
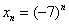
Наше увлекательное путешествие в мир последовательностей подошло к концу и, надеюсь, оно составило достойную конкуренцию Вконтакте =) =) =)
Пример 2: Решение: 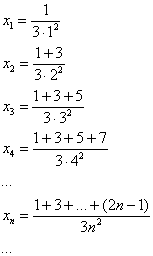
Найдём предел последовательности: 
Используем формулу суммы 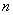
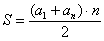
В данном случае 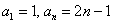
Пример 4: Решение:
Пример 6: Решение:
Пример 8: Решение:
Пример 10: Решение: последовательность 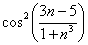
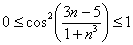
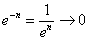
Пример 12: Решение: 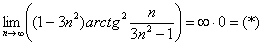
Заменим бесконечно малую эквивалентной: 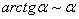
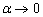
В данном примере 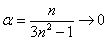
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5