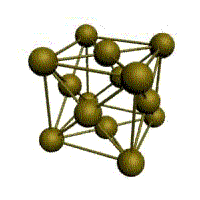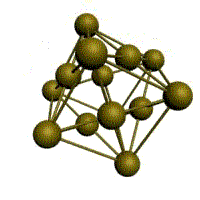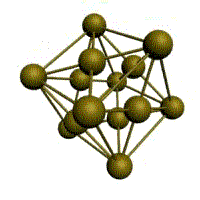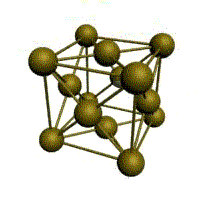
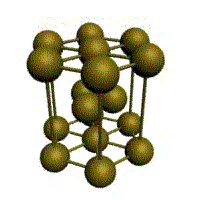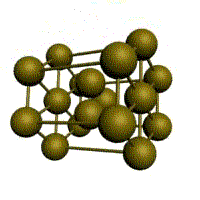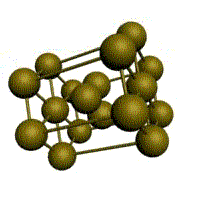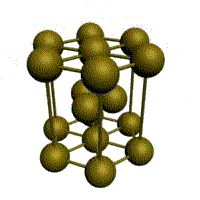
Подпишите что обозначают элементы ячейки материаловедение
1 Элементарная ячейка кристаллической решетки и ее характеристики
1. Элементарная ячейка кристаллической решетки и ее характеристики. Полиморфизм, анизотропия, их использование в технике.
Кристаллическое тело характеризуется правильным расположением атомов в пространстве. У аморфных веществ расположение атомов случайно. Кристаллические вещества образуют кристаллическую решётку. 14 типов кристаллических решёток. Крист. решётка характеризуется элементарной ячейкой. Эл. ячейка – кристаллич. решётка наименьшего объёма, воспроизведение которой в пространстве множество раз создаёт пространственную крист. решётку. Атомы в пространстве располагаются упорядоченно, образуя кристаллическую решётку. Основные типы:
1. Простая кубическая решётка: в узлах кубика атомы касаются друг друга. Параметры: Период решётки (расстояние между атомами a =d), d – диаметр атома. 1/8·8 =1 атом на элемент, ячейку. Для химического соединения данный тип решётки.
2. Кубическая объёмно-центрированная решётка 
3. Кубическая гранецентрированная решётка 
3. Анизотропия кристалла и изотропия кристаллических тел.
Анизотропия – это различие свойств в разных направлениях в кристалле. В монокристалле – анизотропия. Поликристаллические вещества – где много кристаллов. В поликристаллическом теле – изотропия (одинаковые свойства по разным направлениям).
4. Элементарная ячейка; координационное число; сингония
4. Элементарная ячейка; координационное число; сингония
Кристаллографические направления и плоскости, анизотропия; межплоскостные расстояния Кристаллическая решетка – упорядоченное расположение атомов. Элементарная ячейка кристалла – минимальный объем кристалла, полностью сохраняющий все его свойства. Атомы в решетке располагаются различно.
Элементарная ячейка повторяется в трех измерениях и образует кристаллическую решетку. Структуру кристалла определяет положение атомов в элементарной ячейке.
Координационное число – общее число нейтральных молекул и ионов, имеющих связь с центральным ионом в комплексе.
1. У элементов четвертой группы ковалентная насыщенная и направленная связь, и у каждого атома четыре соседа. Число ближайших соседей – координационное число. Элементарная решетка – тетраэдр с одним атомом в центре и четырьмя атомами по вершинам.
2. При образовании ионной связи кристаллические решетки более компактны, координационное число достигает 6 из-за ненасыщенности ионной связи. Пример: кристаллическая решетка NaCI – примитивный куб с ионами хлора и натрия в вершинах.
3. Металлические связи делают кристаллические решетки более компактными. Координационные числа достигают значений 8 и 12. В металлических материалах формируются три типа кристаллических решеток: объемноцентрированная кубическая (ОЦК), гранецентрированная кубическая (ГЦК) и гексагональная плотно-упакованная (ГП).
Сингония – одно из подразделений кристаллов по признаку симметрии их элементарной ячейки при одинаковых системах координатных осей. Сингония характеризует симметрию трехмерных структур с трансляционной симметрией в трех направлениях.
Выделяют семь осевых систем в зависимости от длины отрезков, отсекаемых на кристаллографических осях, и взаимного расположения этих осей.
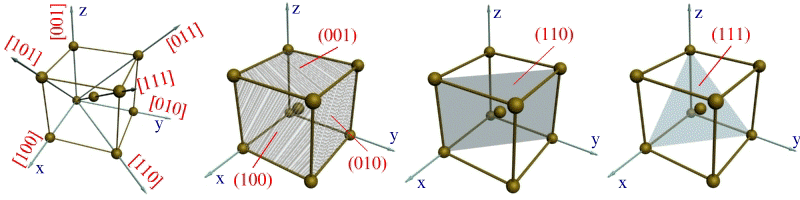
1. Кубическая сингония. Три равновеликие оси пересекаются под прямым углом.
2. Тетрагональная сингония. Два отрезка оси одинаковой длины пересекаются под прямым углом, третья ось перпендикулярна им, и отсекаемый на ней отрезок иной длины.
3. Ромбическая сингония. Три оси разной длины пересекаются под прямыми углами.
4. Моноклинная сингония. Две оси разной длины пересекаются под косым углом, третья ось составляет с ними прямой угол.
5. Триклинная сингония. Три оси разной длины пересекаются под косыми углами.
6. Тригональная сингония. Три отрезка осей равной длины пересекаются в одной плоскости под углом 60 °C, третья ось перпендикулярна этой плоскости, и отсекаемый на ней отрезок имеет иную длину.
7. Гексагональная сингония. Положение осей аналогично их положению в тригональной сингонии.
Упорядоченность расположения атомов в кристаллической решетке позволяет выделить отдельные кристаллографические направления и плоскости.
Кристаллографические направления – прямые лучи, выходящие из любой точки отсчета, вдоль которых располагаются атомы. Точки отсчета – вершины куба. Кристаллографические направления – ребра и диагонали граней куба. Могут быть и другие направления. Кристаллографические плоскости – плоскости, на которых лежат атомы.
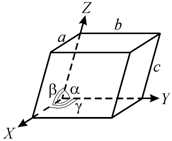
Кристаллографические направления и плоскости характеризуются индексами Миллера, которые определяют их различные положения. Параллельные плоскости в кристаллической решетке, построенные идентично, имеют одинаковые индексы. Чтобы индексы получались из простых целых чисел, плоскость можно смещать параллельно. Положение любого узла кристаллической решетки относительно произвольно выбранного начала координат определяют заданием координат х, у, z. Для одной элементарной ячейки эти координаты равны параметрам решетки а, b, с соответственно.
Для определения индекса находят координаты ближайшего к точке отсчета атома, лежащего на этом направлении, выраженные через параметр решетки.
Все физические, включая и прочностные, свойства металлов вдоль различных кристаллографических направлений зависят от числа атомов, расположенных на упомянутых направлениях. В кристаллической решетке на различных направлениях находится разное число атомов. В кристаллических веществах должна наблюдаться анизотропия, т. е. неодинаковость свойств вдоль различных направлений.
Анизотропия – результат упорядоченного расположения атомов в кристаллических телах, проявляется в пределах монокристалла. Реальные металлы – тела поликристаллические, включающие многочисленные зерна, произвольно ориентированные друг к друг своими кристаллографическими направлениями и плоскостями. Анизотропия механических свойств наблюдается при испытании образцов, вырезанных вдоль различных кристаллографических направлений.
Реальные металлы имеют усредненную изотропность и называются квазиизотропными или псевдоизотропными телами
Межплоскостное расстояние – кратчайшее расстояние, разделяющее параллельные и равноотстоящие друг от друга узловые плоскости.
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес
Читайте также
Вероятное число соударений метеоритов с ракетой в районе орбиты Земли **
11.1. Число и величина
11.1. Число и величина Во времена Пифагора и ранних пифагорейцев руководящую высоту в греческой математике занимало понятие числа. Пифагорейцы считали: Бог положил числа в основу мирового порядка. Бог — это единство, а мир — множественность. Божественная гармония в
36. Ламинарный и турбулентный режимы движения жидкости. Число Рейнольдса
8.2.3.6.2 Число колонок
8.2.3.6.2 Число колонок Должно быть указано число колонок, используемых при оформлении страниц документа.Примечание — Наиболее часто в документации пользователя программного средства используют одноколонное оформление страниц, но может быть также использовано
41. Передаточное число для рычажно-зубчатых индикаторов
41. Передаточное число для рычажно-зубчатых индикаторов Передаточное число для рычажно-зубчатых индикаторов можно вычислить двумя способами:1) где I – длина плеча последнего рычага; R – длина плеча первого рычага; – произведение передаточного числа зубчатых пар;2) где
Подпишите что обозначают элементы ячейки материаловедение
Одним из основных представлений, связанных со структурой кристаллов, является понятие об элементарной ячейке. В общем случае элементарную ячейку можно представить, как минимальный объём кристалла, параллельные переносы (трансляции) которого в трёх измерениях позволяют построить всю кристаллическую решётку.
Закономерности строения элементарной ячейки, в частности степень их симметричности определяет многие свойства кристалла, в первую очередь электрические, магнитные и механические. Элементарная ячейка может содержать как один, так и несколько атомов. Так у многих металлов, например железа, хрома, меди, серебра, она состоит из одного атома. В тех случаях когда, кристалл состоит из нескольких химических элементов, например, натрия и хлора, элементарная ячейка будет содержать два атома: натрий и хлор. Широко распространены кристаллы с элементарной ячейкой, состоящей из нескольких сцепленных друг с другом молекулярных групп, например кристаллы льда или же многих магнитных материалов. Существуют кристаллы, например, белковые, элементарная ячейка которых состоит из молекул, содержащих несколько тысяч атомов.
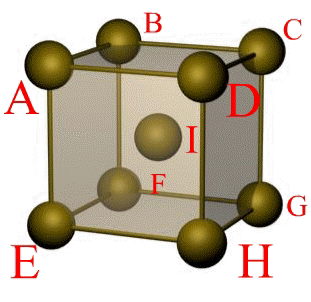
Каждый узел, находящийся в вершине элементарной ячейки, принадлежит еще восьми соседним элементарным ячейкам. Поскольку всего узлов (или вершин параллелепипеда) восемь, то ( 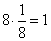
Казалось бы, что выбор элементарной ячейки произволен. На рис. 1.6 все три плоские ячейки примитивны. Хотя трансляции в двух из них и не являются кратчайшими, но любая из них воспроизводит при переносе параллельно самой себе в двух направлениях всю «структуру кристалла». Однако Бравэ были сформулированы 3 правила выбора элементарных ячеек, выполняемые в указанной ниже последовательности.
1. Симметрия элементарной ячейки должна соответствовать симметрии кристалла.
2. Элементарная ячейка должна иметь максимальное число равных ребер и равных углов.
3. При условии выполнения двух первых правил элементарная ячейка должна иметь минимальный объем.
При выполнении этих правил элементарная ячейка, в отличие от примитивной, кроме узлов в вершинах, может иметь дополнительные узлы.
Рис. 1.5. Элементарная ячейка
Рис. 1.6. Различные способы выбора элементарных ячеек
Совокупность координат всех узлов, приходящихся на элементарную ячейку, часто называют ее базисом. Сложную ячейку обычно выбирают так, чтобы узлы находились либо в центрах граней, либо в центре объема. Поэтому принята система наиболее распространенных видов сложных ячеек.
Приведем примеры сложных элементарных ячеек в узлах которых находятся атомы одного сорта.
Кристаллическая решётка. Элементарная ячейка



Структура кристалла– это конкретное расположение частиц в пространстве (физическая реальность). Чтобы представить структуру кристалла, нужно знать относительные размеры частиц, расстояния между ними, силы связи между частицами, их взаимное расположение, повторяющее расположение частиц в пространстве (пространственную решётку), и законы симметрических преобразований.
Симметрия– основная особенность, характерная для структуры кристаллов. Теорию строения структуры кристаллов развил английский учёный Бравэ, основываясь на многих экспериментальных результатах других исследователей. Положив в основу своей теории анизотропию и симметрию кристаллов, он пришёл к понятию о пространственной решётке.
Рис. 1.11.Пространственные решётки некоторых веществ
Рассмотрим простейший случай, когда одинаковые частицы расположены в кристалле параллельными бесконечными рядами. На 1 мм в кристалле находится порядка 10 7 частиц (рис. 1.12). Трансляция(период идентичности) –симметричное преобразование, при котором точка (частица) повторяется в пространстве. Её величина – кратчайшее из возможных расстояний между одинаковыми точками в ряду.
Рис. 1.12.Линейная цепочка атомов
Если сдвинуть точки бесконечного ряда на один период идентичности вдоль направления трансляции, то ряд совместится сам с собой, его вид не нарушится. Выбор основных трансляций в структуре кристалла очень важен, потому что ими определяются кристаллографические системы координат. В общем случае это косоугольные координаты с разными масштабными отрезками по осям (рис. 1.13).
Узлы ряда– одинаковые точки, связанные между собой величиной трансляции ав бесконечном ряду. При перенесении точек по трём направлениям на величину трансляций а, b, c можнополучить трёхмерную сетку.
Ячейки сетки– параллелограммы, вершины которых являются узлами.
Элементарная ячейка– параллелепипед с характерным для данной решётки расположением частиц, с помощью которого весь кристалл может быть построен путём его многократного повторения в трёх направлениях. Она строится на трёх элементарных трансляциях а, b, с. Элементарную ячейку принято выбирать так, чтобы она удовлетворяла следующим условиям: наилучшим образом отражала симметрию сетки, имела бы прямые углы и, если возможно, обладала бы наименьшим объёмом.
Примитивнойназывается элементарная ячейка, внутри которой нет узлов, частицы содержатся только в вершинах (рис. 1.13). Узлы решётки– вершины ячеек, в которых располагаются одинаковые атомы или группы атомов. Они эквивалентны друг другу.
Период (постоянная) кристаллической ячейки– расстояние между однородными атомами. Параметры элементарной ячейки: три ребра ячейки a, b, c; три угла между ними α, β, γ. Например, для представленной на рис. 1.13 примитивной ячейки, соотношения между параметрами следующие:
 |
Рис. 1.13.Примитивная элементарная ячейка
Элементарные ячейки, составляющие кристаллическую решётку кристалла, имеют одинаковые форму и объём. Кристалл можно построить с помощью разных примитивных ячеек. В некоторых случаях удобно характеризовать пространственную сетку не примитивной, а сложной элементарной ячейкой, у которой узлы есть не только в вершинах, но и внутри ячейки. Элементарная ячейка может содержать несколько примитивных ячеек.
Элементарные ячейкиразличаются по элементам симметрии и степени заполнения атомами (рис. 1.14).
Рис. 1.14.Разные примитивные ячейки в плоской сетке
К элементам симметрииотносятся: трансляции, плоскости симметрии, зеркальные плоскости, оси симметрии разных порядков, инверсионные оси симметрии (рис. 1.15).
Рис. 1.15. Элементы симметрии в кубическом кристалле
Кристаллические ячейки делятся по элементам симметрии на 7 сингоний:триклинная, моноклинная, ромбическая, ромбоэдрическая, гексагональная, тетрагональная, кубическая. Сингония в дословном переводе – сходноугольность. В сингонию объединяют кристаллы, у которых одинакова симметрия элементарных ячеек и одинаковая система координат.На рис. 1.16 показана тетрагональная ячейка.
Рис. 1.16. Кристаллическая ячейка тетрагональной сингонии
В каждой сингонии элементарные ячейки делятся по степени заполнения их атомами. Так на одну ячейку простой кубической ячейки имеет приходится 1 атом: n = (1/8)8 = 1; объёмноцентрированной кубической ячейки (ОЦК) – 2 атома: n = (1/8)8 + 1 = 2; гранецентрированной кубической ячейки (ГЦК) – 4 атома: n =(1/8)8 + (1/2)6 = 4 Рис. 1.17); гексагональной с плотной упаковкой (ГПУ) – 2 атома.
Рис. 1.17. Кристаллические ячейки
Кристаллическую решетку общего типа называют решеткой с базисом(БЦК). Решетка с базисом представляется в виде двух вставленных одна в другую подрешеток Бравэ, каждая из которых определяется трансляционными векторами. Базисный вектор устанавливает смещение решеток друг относительно друга. Количество базисных векторов может быть сколь угодно большим.
Рис. 1.18.Решётки Браве
Все известные в природе кристаллические тела кристаллизуются в 14 решётках Браве(рис. 1.18). Далее они делятся на 32 класса симметрии и 230 пространственных групп.
Некоторым телам свойственна не одна, а две или более кристаллических структур, устойчивых при различных температурах и давлениях. Такое явление называется полиморфизмом.Полиморфные формы (модификациивещества) имеют, например, углерод и олово. Углеродможет существовать в виде алмаза и графита. Алмаз очень прочный и твёрдый, графит – хрупкий. Элементарные ячейки алмаза и графита относятся к различным сингониям (рис. 1.19).
Рис. 1.19.Кристаллические решётки алмаза и графита
Оловоможет существовать в виде двух модификаций – серого и белого. Серое оловопри температурах ниже 13,3 °С. имеет решётку типа алмаза. При температурах выше 13,3 °С серое олово превращается в белое олово – очень хрупкое вещество, которое легко разрушается в порошок. Белое (металлическое) оловоимеет тетрагональную объёмноцентрированную решётку.
ИНДЕКСЫ МИЛЛЕРА
Для описания кристаллических многогранников и структур применяется метод индицирования.Через узлы кристаллической решетки можно провести прямые линии и плоскости. Выберем один из узлов решётки за начало координат.
Любой другой узел решётки определяется радиус–вектором:
Индексы узла– три простых числа [[mnp]], взятые в двойные квадратные или фигурные скобки (рис. 1.20). В системе параллельных прямых всегда можно выделить прямую линию (ряд), проходящую через начало координат. Тогда направление прямой линии определится двумя точками: началом координат и любым узлом ряда.
Индексы направления(прямой линии) – три простых числа [mnp], взятые в квадратные скобки. Эти числа характеризуют положение ближайшего узла, лежащего на прямой линии, проходящей через начало координат.
Рис. 1.20.Миллеровские индексы узлов
Проходящая сквозь узлы прямая, а также ребро кристаллического многогранника имеют наклон в выбранной системе координат. В целом плоские сетки в пространственной решётке и соответствующие им грани кристаллического многогранника имеют наклон в системе координат.
Пусть некоторая плоскость решётки пересекает все три оси координат, отсекая на них отрезки ma, nb, pc. Отношение чисел m:n:p характеризует наклон плоскости к осям координат. Серию отношений рациональных чисел m:n:p для всех параллельных плоскостей можно заменить отношением взаимно простых чисел р:q:r. Числа р, q, r называются параметрами Вейса.
Миллеровские индексы плоскости– три простых числа (HKL), записанные в круглых скобках. Индексы плоскости – дополнительные множители к величинам, обратно пропорциональным числу осевых единиц, отсекаемых любой плоскостью данного семейства на координатных осях Х, У, Z.
Миллеровские индексы определяются из соотношения чисел р:q:r.
Пусть некоторая плоскость отсекает на осях координат отрезки:
р =1, q = 3, c = 2 (рис. 1.21). Составим отношения:
 |
Общий знаменатель равен 6. Дополнительные множители: H = 6, K = 2, L = 3.
Миллеровские индексы данной плоскости (623).
Рис.1.21. Индексы плоскости(623)
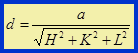
а– постоянная решётки.
В 1819 г. Гаюи сформулировал законцелых чисел(теперь закон Гаюи): для любых двух граней реального кристалла двойные отношения параметров равны отношению малых чисел. На кристаллографическом многограннике образуются лишь такие грани, для которых двойные отношения отрезков, отсекаемых данной гранью и единичной гранью на трёх рёбрах кристалла, принятых за оси координат, равны отношению целых небольших простых чисел.
Грани, для которых отношение р:q:r является иррациональным, в реальном кристалле невозможны. Наклон всякой грани можно определить тремя целыми числами, если за оси координат выбрать направление трёх рёбер кристалла, а за параметры – отрезки, отсекаемые на этих осях данной гранью.
Подпишите что обозначают элементы ячейки материаловедение

1.1. Аморфные и кристаллические тела
В твердых телах атомы могут размещаться в пространстве двумя способами:
Аморфные вещества обладают формальными признаками твердых тел, т.е. они способны сохранять постоянный объем и форму. Однако они не имеют определенной температуры плавления или кристаллизации.
Внешние электронные орбиты атомов соприкасаются, так что плотность упаковки атомов в кристаллической решетке весьма велика.
В кристаллитах соблюдаются ближний и дальний порядки. Это означает наличие упорядоченного расположения и стабильности как окружающих данный атом ближайших его соседей (ближний порядок), так и атомов, находящихся от него на значительных расстояниях вплоть до границ зерен (дальний порядок ).
Рис. 1.1. Расположение атомов в кристаллическом (а) и аморфном (б) веществе
Вследствие диффузии отдельные атомы могут покидать свои места в узлах кристаллической решетки, однако при этом упорядоченность кристаллического строения в целом не нарушается.
1.2. Основные типы кристаллических решеток
Все металлы являются кристаллическими телами, имеющими определенный тип кристаллической решетки, состоящей из малоподвижных положительно заряженных ионов, между которыми движутся свободные электроны (так называемый электронный газ). Такой тип структуры называется металлической связью.
Тип решетки определяется формой элементарного геометрического тела, многократное повторение которого по трем пространственным осям образует решетку данного кристаллического тела.
объемно-центрированная кубическая (ОЦК)
гранецентрированная кубическая (ГЦК)
гексагональная плотноупакованная (ГП)
(6 атомов на ячейку)
Рис. 1.2. Основные типы кристаллических решеток металлов
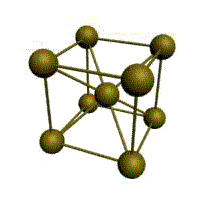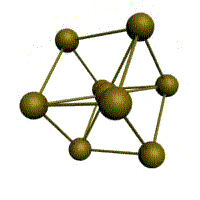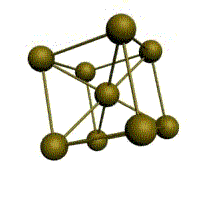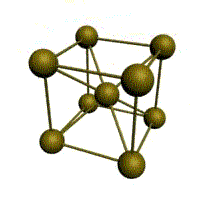
Основу ОЦК-решетки составляет элементарная кубическая ячейка (рис. 1.2,б), в которой положительно заряженные ионы металла находятся в вершинах куба, и еще один атом в центре его объема, т. е. на пересечении его диагоналей. Такой тип решетки в определенных диапазонах температур имеют железо, хром, ванадий, вольфрам, молибден и др. металлы.
У ГЦК-решетки (рис. 1.2, в) элементарной ячейкой служит куб с центрированными гранями. Подобную решетку имеют железо, алюминий, медь, никель, свинец и др. металлы.
Третьей распространенной разновидностью плотноупакованных решеток является гексагональная плотноупакованная (ГПУ, рис. 1.2, г). ГПУ-ячейка состоит из отстоящих друг от друга на параметр с параллельных центрированных гексагональных оснований. Три иона (атома) находятся на средней плоскости между основаниями.
У гексагональных решеток отношение параметра с/ а всегда больше единицы. Такую решетку имеют магний, цинк, кадмий, берилий, титан и др.
Компактность кристаллической решетки или степень заполненности ее объема атомами является важной характеристикой. Она определяется такими показателями как параметр решетки, число атомов в каждой элементарной ячейке, координационное число и плотность упаковки.
Параметры а кубических решеток металлов находятся в пределах от 0,286 до 0,607 нм. Для металлов с гексагональной решеткой а лежит в пределах 0,228-0,398 нм, а с в пределах 0,357- 0,652 нм.
Параметры кристаллических решеток металлов могут быть измерены с помощью рентгеноструктурного анализа.
При подсчете числа атомов в каждой элементарной ячейке следует иметь в виду, что каждый атом входит одновременно в несколько ячеек. Например, для ГЦК-решетки, каждый атом, находящийся в вершине куба, принадлежит 8 ячейкам, а атом, центрирующий грань, двум. И лишь атом, находящийся в центре куба, полностью принадлежит данной ячейке.
Таким образом, ОЦК- и ГЦК-ячейки содержат соответственно 2 и 4 атома.
Под координационным числом понимается количество ближайших соседей данного атома.
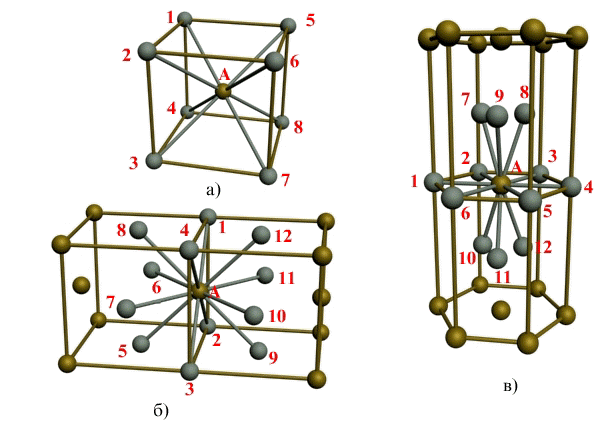
Рис. 1.3. Координационное число в различных кристаллических решетках для атома А:
В ОЦК решетке (рис. 1.3, а) атом А (в центре) находится на наиболее близком равном расстоянии от восьми атомов, расположенных в вершинах куба, т. е. координационное число этой решетки равно 8 (К8).
В ГЦК решетке (рис. 1.3, б) атом А (на грани куба) находится на наиболее близком равном расстоянии от четырех атомов /, 2, 3, 4, расположенных в вершинах куба, от четырех атомов 5, 6, 7, 8, расположенных на гранях куба, и, кроме того, от четырех атомов 9, 10, 11, 12, принадлежащих расположенной рядом кристаллической ячейке. Атомы 9, 10, 11, 12 симметричны атомам 5, 6, 7, 8. Таким образом, ГЦК решетки координационное число равно 12 (К12).
В ГПУ решетке при с/а = 1,633 (рис. 1.3, в) атом А в центре шестигранного основания призмы находится на наиболее близком равном расстоянии от шести атомов /, 2, 3, 4, 5, 6, размещенных в вершинах шестигранника, и от трех атомов 7, 8, 9, расположенных в средней плоскости призмы. Кроме того, атом А оказывается на таком же расстоянии еще от трех атомов 10, 11, 12, принадлежащих кристаллической ячейке, лежащей ниже основания. Атомы 10, 11, 12 симметричны атомам 7, 8, 9.
Следовательно, для ГПУ решетки координационное число равно 12 (Г12).
Плотность упаковки представляет собой отношение суммарного объема, занимаемого собственно атомами в кристаллической решетке, к ее полному объему. Различные типы кристаллических решеток имеют разную плотность упаковки атомов. В ГЦК решетке атомы занимают 74 % всего объема кристаллической решетки, а межатомные промежутки («поры») 26 %. В ОЦК решетке атомы занимают 68 % всего объема, а «поры» 32 %. Компактность решетки зависит от особенностей электронной структуры металлов и характера связи между их атомами.
От типа кристаллической решетки сильно зависят свойства металла.
1.3. Кристаллографические направления и плоскости
Упорядоченность кристаллического строения в пространственной решетке позволяет выделить отдельные кристаллографические направления и плоскости.
Кристаллографическими плоскостями являются, например, плоскости граней кубов (рис. 1.4, б), а также их различные диагональные плоскости вместе с находящимися на них атомами (рис. 1.4, в, г). Для ГПУ-решеток кристаллографическими плоскостями могут быть плоскости оснований (рис. 1.2, г).
Для определения индекса какого-либо направления необходимо найти индекс ближайшего к данной точке отсчета атома, находящегося на данном направлении. Например, индекс ближайшего атома вдоль оси ОХ обозначается цифрами 100 (рис. 1.4,а). Эт и цифры представляют собой координаты упомянутого атома относительно точки О, выраженные через количество параметров вдоль осей OX, OY и OZ соответственно.
Индексы направления ОХ и параллельных ему направлений обозначаются [100]. Соответственно направления OY и OZ обозначаются [010] и [001]. Кристаллографические направления вдоль диагоналей граней XOZ, XOY и YOZ обозначают [101], [110] и [011]. Пользуясь указанной методикой, можно определить индекс любого направления. Например, индекс направления вдоль диагонали куба выразится так: [111].
Индексами плоскостей, параллельных плоскостям XOZ и YOZ, окажутся выражения (010) и (100) (рис. 1.4, б). Индекс вертикальной диагональной плоскости куба выразится через (110), (рис. 1.2, в), а индекс наклонной плоскости, пересекающейся со всеми тремя осями координат на удалении одного параметра, примет вид (111) (см. рис. 1.4, г).
1.4. Анизотропия в кристаллах
Под анизотропией понимается неодинаковость механических и других свойств в кристаллических телах вдоль различных кристаллографических направлений. Она является естественным следствием кристаллического строения, так как на различных кристаллографических плоскостях и вдоль различных направлений плотность атомов различна.
Например, в кубических решетках (см. рис. 1.2, б, в) по направлениям вдоль ребер насчитывается меньше атомов, чем вдоль диагоналей куба в ОЦК-решетке или диагоналей граней в ГЦК-решетке. На плоскостях, проходящих через грани ОЦК- и ГЦК-решеток, находится меньше атомов, чем на диагональных плоскостях.
Поскольку механические, физические и химические свойства вдоль различных направлений зависят от плотности находящихся на них атомов, то перечисленные свойства вдоль различных направлений в кристаллических телах должны быть неодинаковыми.
Анизотропия проявляется только в пределах одного монокристалла или зерна-кристаллита. В поликристаллических телах она не наблюдается из-за усреднения свойств по каждому направлению для огромного количества произвольно ориентированных друг относительно друга зерен. Поэтому реальные металлы являются квазиизотропными телами, т. е. псевдоизотропными.
Рис. 1.5. Элементарная ячейка решетки ОЦК
Сдвиг в кристалле происходит наиболее легко вдоль атомных плоскостей с наиболее плотной упаковкой атомов. Рассмотрим объемно-центрическую кубическую решетку (ОЦК) (рис. 1.5):
Рис. 1.6. Плоскости решетки ОЦК
1.5. Аллотропия металлов
Некоторые металлы, например, железо, титан, олово и др. способны по достижении определенных температур изменять кристаллическое строение, т. е. изменять тип элементарной ячейки своей кристаллической решетки. Это явление получило название аллотропии или полиморфизма, а сами переходы от одного кристаллического строения к другому называются аллотропическими или полиморфными.
На рис. 1.7 показано изменение свободной энергии F от температуры t для двух вариантов кристаллического строения железа: ОЦК (кривая 1 ) и ГЦК (кривая 2).
В интервале температур 911-1392 о C железо имеет решетку ГЦК, так как при этом его свободная энергия меньше. При t 1392°С, у него должна быть решетка ОЦК, обладающая меньшей свободной энергией.
1.6. Дефекты кристаллической решетки металла
Кристаллическая решетка, в которой отсутствуют нарушения сплошности и все узлы заполнены однородными атомами называется идеальной кристаллической решеткой металла.
В решетке реального металла могут находиться различные дефекты.
Все дефекты кристаллической решетки принято делить на точечные, линейные, поверхностные и объемные.
Точечные дефекты соизмеримы с размерами атомов. К ним относятся вакансии, т. е. незаполненные узлы решетки, межузельные атомы данного металла (рис 1.8), примесные атомы замещения, т. е. атомы, по диаметру соизмеримые с атомами данного металла и примесные атомы внедрения, имеющие очень малые размеры и поэтому находящиеся в междоузлиях (рис 1.9). Влияние этих дефектов на прочность металла может быть различным в зависимости от их количества в единице объема и характера.
Рис. 1.8. Схема образования пары вакансия-внедренный атом
Рис. 1.9. Примесные атомы внедрения и замещения
Линейные дефекты имеют длину, значительно превышающую их поперечные размеры. К ним относятся дислокации, т. е. дефекты, образующиеся в решетке в результате смещений кристаллографических плоскостей.
Дислокации бывают двух видов.
Наиболее характерной является краевая дислокация (рис. 1.10). Она образуется в результате возникновения в решетке так называемой полуплоскости или экстраплоскости.
Рис. 1.10. Схема краевой дислокации в идеальном кристалле
Нижний ряд экстраплоскости собственно и принято называть дислокацией.
Другим типом дислокации является винтовая дислокация, которая представляет собой некоторую условную ось внутри кристалла, вокруг которой закручены атомные плоскости (рис.1.11).
Рис. 1.11. Схема винтовой дислокация
В винтовой дислокации, так же как в краевой, существенные искажения кристаллической решетки наблюдаются только вблизи оси, поэтому такой дефект может быть отнесен к линейным.
Дислокации обладают высокой подвижностью, поэтому существенно уменьшают прочность металла, так как облегчают образование сдвигов в зернах-кристаллитах под действием приложенных напряжений.
Дислокационный механизм сдвиговой пластической деформации внутри кристаллов может привести к разрушению изделия. Таким образом, дислокации непосредственно влияют на прочностные характеристики металла.
На рис. 1.12 в виде кривой ABC схематически показана зависимость прочности металла от плотности дислокаций. Точка А соответствует теоретической прочности металла, обусловленной необходимостью одновременного разрыва всех межатомных связей, проходящих через плоскость сдвига, в случае отсутствия дислокаций.
При увеличении количества дислокаций (см. участок АВ) прочность резко снижается, так как на несколько порядков уменьшаются усилия, необходимые для осуществления сдвигов в зернах металла при его деформировании и разрушении.
Рис. 1.12. Зависимость предела прочности кристалла от плотности линейных дефектов(дислокаций). Кривая Одинга
При плотности дислокаций 10 6- 10 7 см-2 (точка В на кривой), прочности минимальна, и на участке ВС происходит ее рост. Это объясняется тем, что с ростом плотности дислокаций их передвижение происходит не только по параллельным, но и по пересекающимся плоскостям, что существенно затрудняет процесс деформирования зерен.
Поэтому начиная с точки В прочность металла возрастает.
Поверхностные дефекты включают в себя главным образом границы зерен (рис.1.13). На границах кристаллическая решетка сильно искажена. В них скапливаются перемещающиеся изнутри зерен дислокации.
Из практики известно, что мелкозернистый металл прочнее крупнозернистого. Так как у последнего меньше суммарная протяженность (площадь) границ. То можно сделать вывод, что поверхностные дефекты способствуют повышению прочности металла. Поэтому создано несколько технологических способов получения мелкозернистых сплавов.
Рис.1.13. Структура границы двух соседних кристаллических зерен
Объемные дефекты кристаллической решетки включают трещины и поры. Наличие данных дефектов, уменьшая плотность металла, снижает его прочность.
Кроме того, трещины являются сильными концентраторами напряжений, в десятки и более раз повышающими напряжения создаваемые в металле рабочими нагрузками. Последнее обстоятельство наиболее существенно влияет на прочность металла.
Контрольные вопросы по лекции №1
В чем состоит существенная разница между строением аморфных и кристаллических тел? Что такое кристаллическая решетка?
Перечислите основные типы ячеек кристаллических решеток металлов. Что такое параметры решеток?
Что понимается под кристаллографическими направлениями и плоскостями и как они обозначаются?
Что такое анизотропия свойств в кристаллах, чем она обусловлена? Привести пример.
Почему поликристаллические тела являются изотропными? Что такое квазиизотропия (псевдоизотропия)?
Что такое аллотропия (полиморфизм) металлов и каково ее практическое значение?
Что представляют собой краевые дислокации, какова их роль в протекании пластической деформации металла и как они влияют на его прочность?
Что такое плотность дислокаций и как она влияет на характер изменения прочности металла?