Почему в металлах эффект холла проявляется гораздо слабее чем в полупроводниках
Эффект Холла и его применение
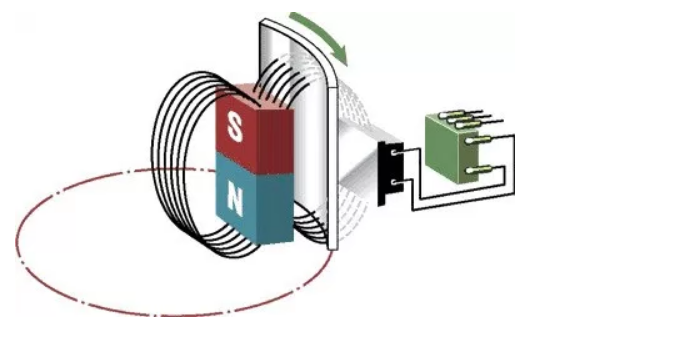
После проведения эксперимента в 1879 году Эдвином Холлом при пропускании магнитного потока через тонкую пластину из золота было обнаружено возникновение на краях пластины разности потенциалов, то есть образовался эффект Холла.
В чем заключается эффект Холла
При помещении в магнитное поле пластины-проводника или полупроводника под 90 ° к направлению силовых линий магнитного потока произойдет перемещение электронов по поперечине пластины под действием силы Лоренца. Их направление зависит от того, в какую сторону идет сила тока и силовые линии магнитного потока. Иначе говоря, (ЭХ) эффект Холла – это частный случай действия силы Лоренца, то есть действия магнитного поля на заряженную частицу.
Это можно рассмотреть на простейшем примере.
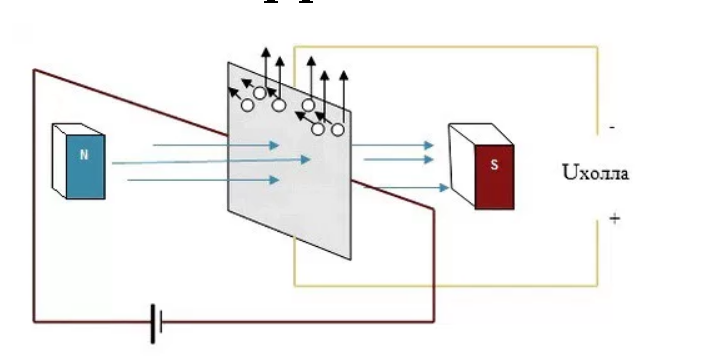
Если представить расположенную к нам торцом пластину, то ее кромка направлена вниз. Она сделана из металла, оба торца подключены к источнику питания, задний из которых на минус, передний на плюс.
Данный случай говорит о том, что электрический ток будет протекать по направлению к наблюдателю. Справа и слева от пластины располагаются два магнита. Правый из них обращен к пластине северным полюсом, левый – южным. Делаем вывод, что данный случай показывает направление силовых линий магнитного поля справа налево, так как они всегда выходят из северного полюса и входят в южный. Силовые линии отклоняют электроны, которые проходят по пластине к ее верхней кромке.
При изменении направления тока в пластине при помощи перемены местами проводников мы сможем наблюдать отклонение электронов вниз. Если направление не менять, а только лишь полюса магнитов, электроны начнут сдвигаться вниз. Когда применяются оба направления, сила Лоренца произведет их перемещение вверх.
Очевидно, что одна из кромок накапливает отрицательный заряд под действием силы Лоренца, на другая на противоположной стороне – положительный. Это говорит о наличии разности потенциалов между ними, то есть электрического напряжения. Увеличение этой разности будет происходить до тех пор, пока не уравновесит силу Лоренца.
Возникновение разности потенциалов в таких случаях, получило название напряжения Холла, которое можно рассчитать, используя формулу:
Аномальный ЭХ
Имеются случаи, когда ЭХ может быть обнаружен в пластине без пропускания через нее магнитного потока. Это возможно при нарушении симметрии по отношению к обращению времени в системе. В частности, аномальный ЭХ способен проявляться в намагниченных материалах.
Квантовый ЭХ
Двумерные газы со средним расстоянием между частицами, уменьшенным до значения длины де Бройля на зависимости поперечного сопротивления к воздействию магнитного поля, подвержены возникновению плато сопротивления в поперечине. ЭХ квантуется только в сильных магнитных полях.
Магнитные потоки, обладающие больше силой индукции, имеют дробный квантовый ЭХ. Он взаимосвязан с перестроением внутренней структуры двумерной электронной жидкости.
Спиновый ЭХ
СЭХ можно наблюдать на не намагниченных проводниках, которые не переместили в поле действия силовых линий магнита. Суть эффекта – отклонение электронов с антипараллельными спинами к противоположным краям пластины.
Применение эффекта Холла
Применение метода Холла связано с изучением особенностей полупроводников. С его помощью стало возможным вычисление количества носителей заряда на единицу объема, а также их подвижность. При его использовании реально отличить электрон от квазичастицы с положительным зарядом.
ЭХ всегда считался основой для разработки датчиков Холла. Аппаратура предназначена для измерения напряженности магнитного поля. Их используют для построения моторов со следящим приводом. В моторах они исполняют роль датчика обратной связи. Они способны измерить угол поворота вала мотора.
Датчики Холла устанавливают в электростартерах ДВС, охлаждающих системах ПК, навигационных системах мобильных телефонов, в измерительных приборах для вычисления количества заряда.
Эффект холла — в чем заключается, применение для датчиков тока и положения, формула, квантовый, аномальный и другие виды
Электричество и магнитные поля существуют в тесной взаимосвязи друг с другом. Многие известные физики посвятили жизнь исследованию этой связи, поиску и описанию законов, на которых она базируется, а также способов применения на практике полученных теоретических сведений. Одним из таких учёных был Эдвин Герберт Холл, выдающийся американский исследователь, автор ценных научных материалов. В ходе одного из экспериментов он обнаружил необычное явление, которое со временем получило название «эффект Холла». Сегодня он массово используется в бытовой и компьютерной технике, электрооборудовании автомобилей, контрольно-измерительных приборах и, конечно, исследовательских лабораториях. Так в чём же физическая суть эффекта Холла и почему он не теряет своей актуальности спустя почти полтора века с момента открытия?
Что такое эффект Холла?
Эдвин Холл, пропуская ток через тонкую золотую пластину, расположенную между двумя магнитами, заметил, что носители заряда (электроны) отклоняются от центральной оси к одной из граней проводника. Таким образом, на этой грани возникает отрицательный заряд, а на противоположной — положительный. Возникшая разность потенциалов именуется холловским напряжением. Она строго перпендикулярна току в проводнике и вектору магнитной индукции. Это явление наблюдается не только в золоте, но и в любых проводниковых и полупроводниковых материалах, помещённых в магнитное поле.
Если проанализировать физическую суть, можно обнаружить, что у истоков накопления заряда на гранях проводника лежит сила Лоренца, с которой магнитное поле воздействует на заряженную частицу. Под её воздействием электроны будут накапливаться на грани проводника до тех пор, пока их суммарный заряд не скомпенсирует существующее магнитное поле.
В том же случае, когда внешнее магнитное поле слишком велико, система выйдет за рамки стабильности, и заряженные частицы начнут двигаться по циклоиде. Это называется несоблюдением критерия малости.
Цифровые датчики Холла делятся на униполярные и биполярные
Помимо эффекта Холла, законы которого описаны классической физикой и соблюдаются во всех нормальных или приближённых к нормальным условиям экспериментах, выделяют ещё несколько разновидностей явления возникновения разности потенциалов в проводнике.
Аномальный
Аномальным называют любой случай накопления заряда на грани проводника, в котором исключено воздействие внешних магнитных полей. Необходимым условием является перпендикулярная направленность разницы потенциалов относительно направления силы тока.
Причины, по которым возникает аномальный эффект Холла, обычно кроются в намагниченности металла-проводника или особенностях его молекулярной структуры.
Квантовый
Законы возникновения разницы потенциалов в «квантовом мире» исследуются на примере плоского проводника типа ДЭГ (двумерный электронный газ). Квантовый наблюдается в сильных магнитных полях и при низких температурах. Он выражается в квантовании холловского сопротивления, которое на графике имеет чётко выраженные «участки плато». Чем выше сопротивление, тем длиннее участки плато и выше разница между ними.
Открытие данного явления — одна из основных вех современной квантовой физики. Клаус фон Клитцинг, первооткрыватель квантового эффекта Холла, в 1985 году был удостоен Нобелевской премии.
Дробный
Многие передовые учёные в 80-х годах прошлого века заинтересовались исследованиями фон Клитцинга и продолжили изучать свойства разности потенциалов в ДЭГ. Наибольших успехов достигли Даниэль Цуи и Хорст Штёрмер, которые проанализировали промежуточные участки между «плато сопротивления» и пришли к выводу, что при существенном увеличении интенсивности магнитных полей «участки плато» можно получить и на дробных значениях электронных уровней Ландау, например, при n=1/3; n=2/5; n=3/7 и т. д.
Такое явление получило название дробного квантового эффекта Холла, а его первооткрыватели получили Нобелевскую премию по физике в 1998 году. В настоящее время ведутся расширенные исследования квантового и дробного квантового видов данного эффекта.
Спиновый
В 2003–2004 годах было изучено поведение электронов с антипараллельными спинами в проводниках, изолированных от каких-либо магнитных полей. Теоретической базой исследования послужили теории Владимира Переля, выдвинутые в далёком 1971 году. Они были доказаны на практике, когда удалось зафиксировать отклонения данных групп электронов к противоположным граням проводника. Движение заряженных частиц напоминает первый вид эффекта — аномальный.
Формулы и расчёты
Поскольку данный эффект базируется на силе Лоренца, то именно с её определения и начинается математическое описание возникшей разницы потенциалов. Сила Лоренца определяется из следующего выражения:
Электрическое поле, сформированное образовавшимися на гранях проводника зарядами, тоже влияет на движущиеся в сечении электроны. Сила этого влияния описывается так:
Когда разность потенциалов уравновешивает магнитное поле, система считается стабильной. При этом соблюдается условие Fл= Fэл. Следовательно, верны и два следующих утверждения:
Скорость электронов обычно определяется с помощью формулы плотности тока:
Теперь электрическое поле E можно описать с помощью выражения:
Найдём разность потенциалов:
Uн=dE=djB/qn, где d — толщина проводящей пластины.
Упростить данное выражение можно с помощью так называемой «постоянной Холла», которая имеет вид R=1/qn. Окончательная формула разности потенциалов примет вид:
То есть, разность потенциалов прямо пропорциональна толщине проводника, магнитной индукции и плотности тока.
Применение
Поскольку данное явление позволяет адекватно оценить концентрацию и подвижность заряженных частиц, проследить чёткую зависимость между силой тока, внешним магнитным полем и поведением электронов в материале, он нашёл широкое применение на практике. В общем виде устройства и приборы, принцип действия которых основан на эффекте Холла, можно разделить на две категории: контрольно-измерительное оборудование для материалов с различной проводимостью и электронные датчики.
В проводниках и полупроводниках
В точном машиностроении рассматриваемый эффект используют для определения электромагнитных свойств и молекулярной структуры материала. В проводниках эти показатели оцениваются посредством анализа движения электронов под воздействием силы тока и магнитных полей, в полупроводниках же с равной эффективностью анализируется как поведение электронов, так и образование электронных дырок. Широкое распространение получил метод ван дер Пау, позволяющий определить:
Метод применим к любому плоскому образцу произвольной формы, толщина которого намного меньше длины исследуемого участка. Он широко используется при первичных расчётах полупроводниковых приборов: диодов, транзисторов, тиристоров и др.
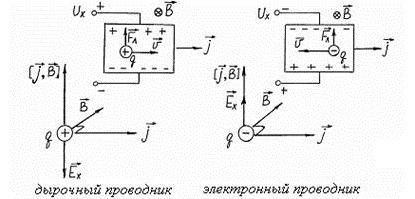
Направление поля Холла в проводниках зависит от их типа
Датчики Холла — назначение и разновидности
Самостоятельные устройства и элементы систем, использующие интересующий нас эффект для измерения магнитоэлектрических величин, называют датчиками Холла. Их делят на две большие группы: аналоговые и цифровые. Аналоговые датчики очень просты и представляют собой, как правило, изолированный источник магнитного поля, действие которого на проводник напрямую зависит от расстояния и полярности. Такие датчики служат для преобразования магнитной индукции в разность потенциалов.
Они необходимы для измерения магнитных полей. Если индукция поля превышает заданный порог срабатывания датчика, то он формирует цифровой сигнал «1», в противном случае значение сигнала – «0». Ввиду наличия «слепых зон», в которых индукция слишком мала для срабатывания датчика, его применение не всегда целесообразно. Цифровые датчики холла делят на:
Датчики Холла встречаются в почти любой достаточно сложной электронике — от бесконтактных выключателей до смартфонов, от автомобильных двигателей до ионных двигателей космических кораблей. Способность реагировать на появление и изменение магнитных полей сделала устройство незаменимым в электронике и электромеханике, а отсутствие прямого физического взаимодействия обеспечило высокую надёжность и точность, износостойкость и долговечность датчиков.
Изготовление датчика тока на основе эффекта Холла
Если Вы обладаете хотя бы базовыми навыками в работе с электронными компонентами, то без особого труда сможете самостоятельно сконструировать датчик тока. С его помощью можно будет бесконтактно определять наличие электрического тока в проводнике. Вот полный перечень материалов и инструментов, которые Вам понадобятся:
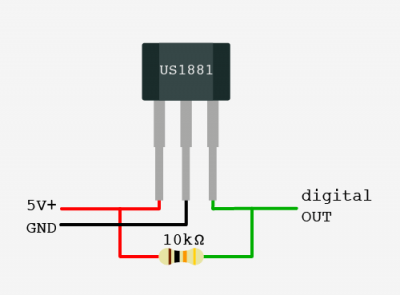
Разверните корпус датчика маркировкой к себе. Нумерация выводов слева направо классическая: 1, 2, 3. Между первой и второй ножкой установите керамический конденсатор ёмкостью 0,1 мкФ (100 нФ). Между первой и третьей ножкой установите резистор сопротивлением 10 кОм. Теперь подключим датчик к плате Arduino по такой схеме:
Устанавливать кермачиеский конденсатор между первой и второй ножками необязательно, но рекомендуется для стабилизации входящего напряжения
Ферритовое кольцо аккуратно распилите пополам с помощью ручного лобзика. Материал твёрдый, но достаточно хрупкий, поэтому работать придётся осторожно. Полученные полукольца очистите от сколов и шероховатостей, после чего приклейте сбоку к «челюстям» зажима-крокодила так, чтобы в сжатом состоянии торцы полуколец едва касались друг друга. На один из торцов наклейте кусочек плотной толстой ткани или резины, на второй — корпус цифрового датчика Холла.
Теперь, поместив внутри разрезанного ферритового кольца проводник и пустив по нему электрический ток, вы сможете наблюдать появление входящего сигнала на плате Arduino.
На сегодняшний день классический эффект Холла полностью изучен и служит теоретической базой для более или менее сложных электронных устройств. Ведутся исследования частных разновидностей эффекта Холла, в том числе поиск способов их использования в электрических, жидко- и газотопливных двигателях нового поколения.
Эффект Холла
Вы будете перенаправлены на Автор24
Описание сути явления
Возникновение разности потенциалов в проводнике с током под воздействием магнитного поля называют эффектом Холла.
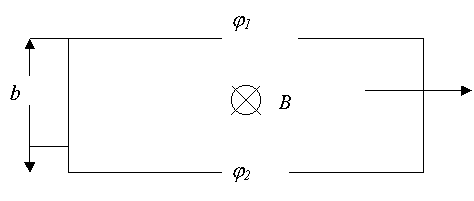
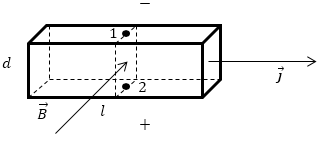
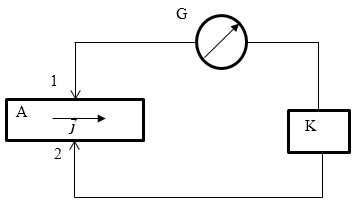
Если в металле создать магнитное поле, которое будет перпендикулярно току, то между точками 1 и 2 (рис.1) возникнет разность потенциалов, которая говорит о том, что при наличии магнитного поля эквипотенциальные поверхности в пластинке отклоняются от первоначального положения. В возникновении поперечной разности потенциалов заключается эффект Холла.
Сущность эффекта Холла
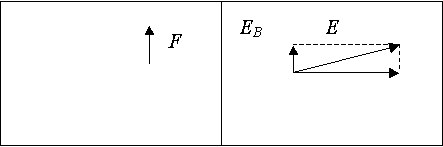
Эффект Холла является следствием существования силы Лоренца. На движущиеся в магнитном поле заряды действует сила Лоренца. Под ее действием электрон отклоняется от первоначального направления движения к одной из граней. В результате одна из граней проводника заряжается отрицательно, следовательно, другая становится положительно заряженной. Внутри металла появляется поперечное электрическое поле ($\overrightarrow
Готовые работы на аналогичную тему
Эмпирически получено, что поперечная разность потенциалов (U), возникающая в эффекте Холла в слабых магнитных полях, может быть рассчитана как:
Значение и применение эффекта Холла
Эффект Холла наблюдается не только в металлах, но и например, в полупроводниках. Опыты по изучению эффекта Холла в разных веществах показали, что он не всегда является результатом движения отрицательных зарядов. Если измерение разности потенциалов в эффекте Холла показывает, что движутся положительные заряды, то такой эффект называют аномальным.
Эффект Холла используют создавая так называемые датчики Холла. Они используются для определения параметров магнитных полей, нахождения местоположения объектов.
Данный эффект используют для изучения энергетического спектра носителей заряда в металлах и полупроводниках.
На эффекте Холла основано действие магнитных насосов для стимулирования циркуляции жидких металлов и других проводящих жидкостей и магнитодинамических генераторов энергии.
Для решения задачи используем формулу:
Подставим (1.2) в (1.1), получим:
Задание: Получите выражение для постоянной Холла, считая, что проводник с током, помещен в магнитное поле. Следует допустить, что электрон движется равномерно.
Плотность тока в проводнике можно выразить как:
Кроме того разность потенциалов между точками 1- 2 (рис.1) равна:
Подставим в (2.5) выражение для напряженности (2.2) и скорость из (2.4), получим:
Выражение для разности потенциалов в эффекте Холла имеет выражение:
Получаем, что постоянная Холла равна:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 10 02 2021
Эффект Холла
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ МОРСКОЙ
Кафедра физики
студент группы 32СУ1
преподаватель Скидан В.В.
Объяснение эффекта Холла с помощью электронной теории
Эффект Холла в ферромагнетиках
Эффект Холла в полупроводниках
Эффект Холла на инерционных электронах в полупроводниках
Список используемой литературы
Рис 1.1
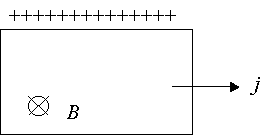
здесь магнитное поле перпендикулярно плоскости пластинки. На середине боковых граней, перпендикулярно току, расположены электроды, между которыми измеряется ЭДС Холла Vx :
Так как ЭДС Холла меняет знак на обратный при изменении направления магнитного поля на обратное, то Холла эффект относится к нечётным гальваномагнитным явлениям.
10 5 (см 3 /кулон). Коэффициент Холла R может быть выражен через подвижность носителей заряда m = е t /m* и удельную электропроводность s = j/E = еnvлр/Е :
Здесь m* — эффективная масса носителей, t — среднее время между двумя последовательными соударениями с рассеивающими центрами.
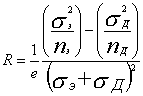
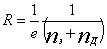
При nэ = nд, = n для всей области магнитных полей :
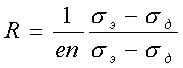
а знак R указывает на преобладающий тип проводимости.
Для металлов величина R зависит от зонной структуры и формы Ферми поверхности. В случае замкнутых поверхностей Ферми и в сильных магнитных полях ( W t »1) коэффициент Холла изотропен, а выражения для R совпадают с формулой 4,б. Для открытых поверхностей Ферми коэффициент R анизотропен. Однако, если направление Н относительно кристаллографических осей выбрано так, что не возникает открытых сечений поверхности Ферми, то выражение для R аналогично 4,б.
2. Объяснение эффекта Холла с помощью электронной теории.
Если металлическую пластинку, вдоль которой течет постоянный электрический ток, поместить в перпендикулярное к ней магнитное поле, то между гранями, параллельными направлениям тока и поля возникает разность потенциалов U= j 1— j 2 (смотри рис 2.1). Она называется Холловской разностью потенциалов (в предыдущем пункте – ЭДС Холла) и определяется выражением:
Последнее выражение совпадает с (2.1), если положить
Из (2.4) следует, что, измерив постоянную Холла, можно найти концентрацию носителей тока в данном металле (т. е. число носителей в единице объема).
Важной характеристикой вещества является подвижность в нем носителей тока. Подвижностью носителей тока называется средняя скорость, приобретаемая носителями при напряженности электрического поля, равной единице. Если в поле напряженности Е носители приобретают скорость u то подвижность их u0 равна:
 | ||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||





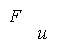
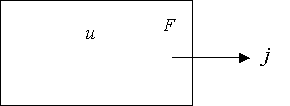



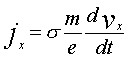 , (1)
, (1)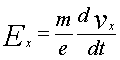 , (2)
, (2)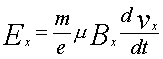 (3)
(3)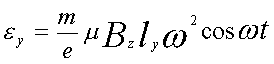 (6)
(6) (7)
(7)