Почему библиотека numpy работает с массивами быстрее чем обычный интерпретатор python
Почему библиотека numpy работает с массивами быстрее чем обычный интерпретатор python
NumPy (Numeric Python, Числовой Python) — это библиотека для работы с многомерными массивами, также включает набор математических функций, которые применяются над ними. За счет собственной оптимизации кода на языке C и Fortran обеспечиваются быстрые вычисления по сравнению с обычными структурами данных в Python.
Особенности
Сферы применения
NumPy нашел большое количество применений в разных сферах деятельности. Перечислим некоторые из них:
Почему NumPy такой быстрый
Быстрота библиотеки обеспечивает за счет векторизации, которая описывает отсутствие каких-либо явных циклов, индексации и т. д. В коде эти вещи происходят «за кулисами» в оптимизированном, предварительно скомпилированном коде C. Векторизованный код имеет множество преимуществ, среди которых:
В основе векторизации лежит класс ndarray – многомерный контейнер элементов одного типа данных и размера (int32, float32 и т.д.). Объекты этого класса занимают меньше памяти, а операции над ними производятся быстрее, чем с обычными списками Python.
Создание массивов
Массивы ndarray могут быть созданы несколькими способами. Например, может создать массив явно:
Однако более удобный способ — это определить размер массива и заполнить его либо случайными значениям, либо значениями по порядку.
Очень часто требуются массивы для инициализации, например, массивы, которые состоят только из нулей или единиц. Этот метод предпочтительней, т.к. не использует затратную генерацию случайных чисел. Такие массивы могут быть созданы следующим образом:
Почему массивы NumPy такие быстрые?
5 ответов
Кроме того, многие операции Numpy реализованы на C, что позволяет избежать общей стоимости циклов в Python, косвенного обращения к указателю и динамической проверки типов для каждого элемента. Повышение скорости зависит от того, какие операции вы выполняете, но несколько порядков нередки в программах сокращения чисел.
У вас еще есть петли, но они сделаны в ц. Numpy основан на Atlas, которая является библиотекой для операций линейной алгебры.
Перед лицом больших вычислений он будет запускать тесты, используя несколько реализаций, чтобы выяснить, какая из них является самой быстрой на нашем компьютере в данный момент. При некоторых сложных сборках вычисления могут распараллеливаться на нескольких процессорах. Таким образом, вы будете иметь высоко оптимизированный c, работающий на непрерывных блоках памяти.
Рассмотрим следующий код:
Здесь Numpy намного быстрее, потому что он использует преимущества параллелизма (что имеет место в случае нескольких данных с одной инструкцией (SIMD)), в то время как традиционный цикл for не может его использовать.
Например. если вы суммируете два массива, добавление будет выполняться с помощью специализированного операции с векторным процессором, вместо вызова реализации Python для добавления int в цикл.
Numpy массивы очень похожи на «нормальные» массивы, такие как в c. Обратите внимание, что каждый элемент должен быть одного типа. Ускорение очень велико, потому что вы можете воспользоваться преимуществами предварительной выборки и мгновенно получить доступ к любому элементу массива по его индексу.
Сравнение скорости. numpy против стандарта Python
Я думаю, что есть тенденция к тому, что стандартная библиотека python примерно в 10 раз быстрее для мелкомасштабных операций, тогда как numpy намного быстрее для крупномасштабных (векторных) операций. Я предполагаю, что numpy имеет некоторые издержки, которые становятся доминирующими для небольших случаев.
Мой вопрос: верна ли моя интуиция? И будет ли вообще целесообразно использовать стандартную библиотеку вместо numpy для небольших (обычно скалярных) операций?
Журнал и экспонента
Создать нормальное распределение
Выбор случайного элемента
То же самое с пустым массивом
С большим массивом
2 ответа
И будет ли вообще целесообразно использовать стандартную библиотеку, а не NumPy для небольших (обычно скалярных) операций?
Редко, когда узкое место для программы вызвано операциями со скалярами. На практике различия незначительны. Так что в любом случае это хорошо. Если вы уже используете NumPy, нет никакого вреда в том, чтобы продолжать использовать операции NumPy в скалярах.
Стоит сделать особый случай вычисления случайных чисел. Как и следовало ожидать, случайное число, выбранное с помощью random против NumPy, может не совпадать:
У вас есть дополнительная функциональность в NumPy, чтобы сделать случайные числа «предсказуемыми». Например, повторный запуск приведенного ниже сценария будет всегда приводить к одному и тому же результату:
Чистый Python против NumPy и TensorFlow. Сравнение производительности
Содержание
Философия Python заключается в том, чтобы позволить программистам выражать концепции в удобной форме и в меньшем количестве строк кода. Эта философия делает язык подходящим для разнообразного набора сценариев: простые сценарии для Интернета, большие веб-приложения (например, YouTube), язык сценариев для других платформ (например, Blender и Autodesk Maya) и научные приложения в нескольких областях, таких как астрономия, метеорология, физика и наука о данных.
Чтобы обойти этот недостаток, появилось несколько библиотек, которые поддерживают простоту использования Python, одновременно предоставляя возможность выполнять численные вычисления эффективным образом. Стоит упомянуть две такие библиотеки: NumPy એ (одна из первых библиотек для обеспечения эффективных численных вычислений в Python) и TensorFlow એ (недавно развернутая библиотека, ориентированная больше на алгоритмы глубокого обучения).
Но как эти схемы сравнивать? Насколько быстрее работает приложение, если оно реализовано с помощью NumPy вместо чистого Python? А как насчет TensorFlow? Цель этой статьи — начать изучение улучшений, которых можно достичь с помощью этих библиотек.
Чтобы сравнить эффективность трех подходов, вы создадите базовую регрессию с помощью нативных Python, NumPy и TensorFlow.
Генерирование тестовых данных
Чтобы сгенерировать обучающую выборку задачи, воспользуйтесь следующей программой:
Примечание. Использование w_opt = np.linalg.inv(X.T @ X) @ X.T @ d даст такое же решение. Для получения дополнительной информации см. Приводим уравнение линейной регрессии в матричный вид.
Хотя этот детерминированный подход можно использовать для оценки коэффициентов линейной модели, это невозможно для некоторых других моделей, таких как нейронные сети. В этих случаях итерационные алгоритмы используются для оценки решения для параметров модели.
Градиентный спуск в чистом Python
Давайте начнем с подхода, основанного на чистом Python, в качестве основы для сравнения с другими подходами. Функция Python ниже оценивает параметры w_0 и w w_1 с помощью градиентного спуска:
Теперь найдём решение:
В каждую эпоху после обновления рассчитывается выход модели. Векторные операции выполняются с использованием списков. Мы также могли бы обновить y на месте, но это не повлияло бы на производительность.
Истекшее время алгоритма измеряется с помощью библиотеки времени. Для оценки w_0 = 2,9598 и w_1 = 2,0329 требуется 18,65 секунды. Хотя библиотека timeit может предоставить более точную оценку времени выполнения, запустив несколько циклов и отключив сборку мусора, в этом случае достаточно простого просмотра одного запуска со временем, как вы вскоре увидите.
Использование NumPy
NumPy добавляет поддержку больших многомерных массивов и матриц вместе с набором математических функций для работы с ними. Операции оптимизированы для работы с молниеносной скоростью, полагаясь на проекты BLAS и LAPACK для базовой реализации.
Используя NumPy, рассмотрим следующую программу для оценки параметров регрессии:
В приведенном выше блоке кода используются векторизованные операции с массивами NumPy ( ndarrays ). Единственный явный цикл for — это внешний цикл, в котором повторяется сама программа обучения. Понимание списков здесь отсутствует, потому что тип ndarray NumPy перегружает арифметические операторы для выполнения вычислений массива оптимальным образом.
Давайте сравним время выполнения. Как вы увидите ниже, поскольку сейчас речь идёт о долях секунды, а не о секундах, здесь для более точного получения времени выполнения нам необходим модуль timeit:
timeit.repeat() возвращает список. Каждый элемент — общее время, затраченное на выполнение number циклов инструкции. Чтобы получить единую оценку времени выполнения, вы можете взять среднее время для одного вызова из нижней границы списка повторов:
Использование TensorFlow
Используя свой Python API, процедуры TensorFlow реализованы в виде графа вычислений, которые необходимо выполнить. Узлы на графе представляют математические операции, а ребра графа представляют собой многомерные массивы данных (также называемые тензорами), передаваемые между ними.
Во время выполнения TensorFlow берет граф вычислений и эффективно запускает его, используя оптимизированный код C++. Анализируя граф вычислений, TensorFlow может идентифицировать операции, которые могут выполняться параллельно.
Эта архитектура позволяет использовать единый API для развертывания вычислений на одном или нескольких процессорах или графических процессорах на настольном компьютере, сервере или мобильном устройстве.
Используя TensorFlow, рассмотрите следующую программу для оценки параметров регрессии:
Когда вы используете TensorFlow, данные должны быть загружены в специальный тип данных, называемый Tensor. Тензоры отражают массивы NumPy во многих отношениях, чем они различны.
После создания тензоров из обучающих данных определяется граф вычислений:
Стоит отметить, что код до создания training_op не выполняет никаких вычислений. Он просто создает граф вычислений, которые необходимо выполнить. На самом деле даже переменные еще не инициализированы. Чтобы выполнить вычисления, необходимо создать сеанс и использовать его для инициализации переменных и запуска алгоритма для оценки параметров регрессии.
Вот та же структура синхронизации кода, которая использовалась с реализацией NumPy:
Однако разница во времени в этом случае незначительна.
Заключение
Цель этой статьи — показать различие производительности реализации простого итеративного алгоритма оценки коэффициентов линейной регрессии на чистом Python, NumPy и TensorFlow.
Приведённые выше скрипты запускались на довольно «пожилом» ноутбуке, со следующими характеристиками:
И вот полученные результаты по времени, затраченному на выполнение алгоритмов этих трёх реализаций:
NumPy vs Python
Сегодня мы рассмотрим, так ли оптимизация NumPy (сокр. от Numeric Python) хороша по сравнению с обычными списками в Python. Главным критерием мы возьмём время вычислений, а тестировать будем три операции: обычное умножение, вычисление гиперболического тангенса и нормализация в промежуток [0, 1].
Вычисление времени в Python
Для вычисления времени мы будем использовать модуль стандартной библиотеки Python — time. Функция time.time() возвращает текущее время в секундах, и именно от этой функции мы будем отталкиваться.
Не забудьте подписаться группу Вконтакте и Telegram-канал. Там можно найти еще больше интересных и полезных материалов по программированию.
Начало работы NumPy
Для начала импортируем все необходимые модули.
Назначение модуля time уже известно. math необходим для доступа к точному значению константы e. random нам необходим для случайного заполнения списка Python, NumPy для тестов массивов np.array и matplotlib для визуализации полученных нами данных.
Умножение
Первая операция, которую мы будем тестировать — обычное умножение. Т.к. массивы NumPy поддерживают векторизированные операции(т.е. операция применяется к каждому элемента массива), то выполнять умножение по отношению к дин.массиву мы будем с помощью listcomp’а.
Простой список, array * n и array.dot
Здесь мы рассмотрим вычисления векторизированного умножения списка, обычного умножения массива NumPy на число и отдельный метод np.array для умножения. Все тестовые блоки будут выглядеть очень похоже:
С помощью random.random() создаём список длиной size, элементы которого принадлежат диапазону [0, 1]. Создаём новый список, элементы которого ровно в 1 миллион раз больше элементов исходного массива. Время вычислений для каждой длины массива заносим в массив.
Далее таким же методом исследуем операцию np.array * n:
Примечание. time.sleep(0.1) здесь нужно из-за того, что некоторые значения будут равны нулю из-за особенности хранения чисел с плавающей точкой в Python.
Тоже самое делаем для метода np.array.dot:
Визуализация
Теперь изобразим график зависимости времени вычислений от длины массива:
Если вы читали другие статьи по Python в Code Blog, то данный фрагмент кода может вас смутить только в 3-ей строке. Да, использовав функцию figure() и передав туда кортеж значений, мы можем изменить размер исходной картинки.
Пройдёмся еще по некоторым «непонятностям»:
Получаем довольно интересный результат:
Как мы можем заметить, выражения array * n и array.dot(n) работают по времени почти одинаково (резкие скачки связаны с тем, что выполняя этот пример, у меня были запущены еще некоторые программы, которые использовали ресурсы процессора).
Почему на отрезке [10000, 30000] время выполнения операций с массивами NumPy больше, чем с обычным списком Python?
Как вы можете помнить, мы добавили в тесты массивов NumPy конструкцию time.sleep(0.1), чтобы избавиться от нулевых значений. Так что для получения полной картины необходимо переместить график списков еще на два «блока» вверх, хотя и без этого всё наглядно продемонстрировано.
Действительно, обычное векторизированное умножение массива длиной один миллион в обычном Python’е займёт 0.35 секунды, что является очень большим числом, учитывая результат NumPy.
Гиперболический тангенс
В следующем примере мы будем измерять скорость вычисления гиперболического тангенса. Для меня эта функцию представляет интерес, поскольку она часто является функцией активации в простом персептроне или нейросети.
Подробнее почитать про эту функцию можно почитать в Википедии, там предоставлен хороший материал.
tanh в Python
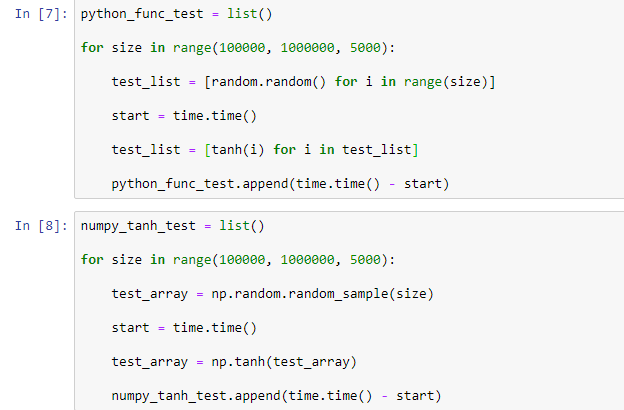
Чтобы предоставить чистоту эксперимента, мы реализуем функцию tanh вручную, а не будем пользоваться math.tanh.
По той же схеме вычисляем время работы каждой функции для разных длин массивов:
Результаты имеются, осталось только их визуализировать:
Здесь опять появляется новая конструкция, применение которой, по моему мнению, нуждается в объяснении.
plt.legend(loc=, fontsize=) — параметр loc указывает на расположение легенды (в нашем случае слева вверху), а fontsize устанавливает размер текста легенды, чтобы сделать её больше.
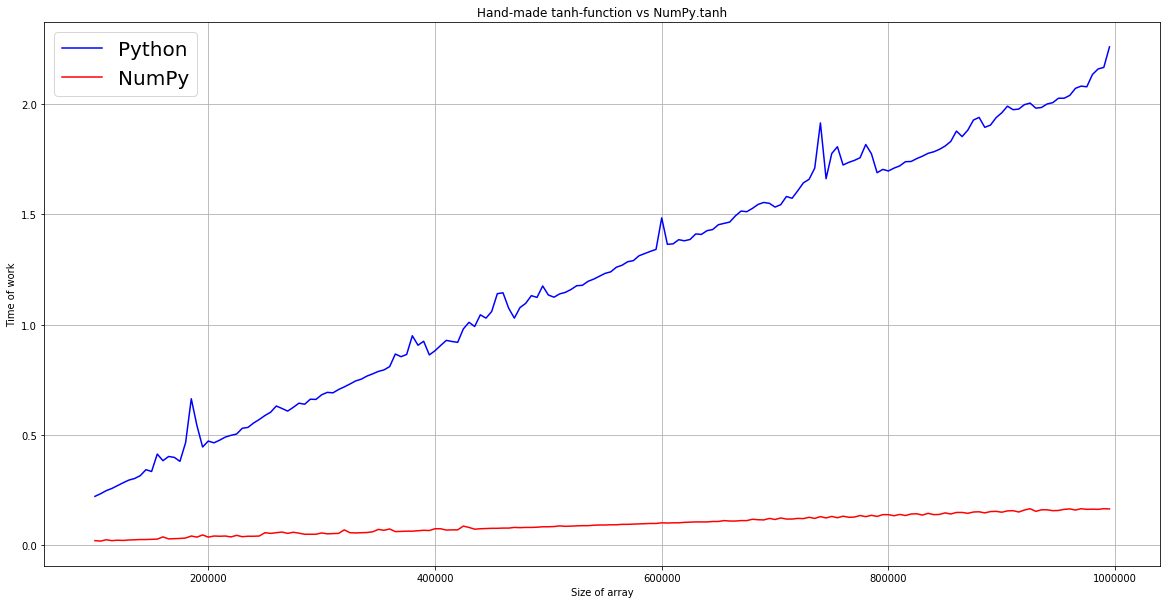
Получаем такой результат:
Как мы можем заметить, для вычисления гиперболического тангенса каждого элемента списка длиной 1 миллион, «питону» потребуется 2 секунды (просто представьте, сколько бы времени занимало обучение нейросети, которая использует значения, которые хранятся в списках!). График зависимости NumPy имеет намного меньший угловой коэффициент, что говорит о быстрой работе даже на огромных массивах данных.
Нормализация
Нормализация — приведение данных к определённому промежутку для улучшения модели машинного обучения (например, тот же самый SVC требует нормализации к промежутку [0, 1]).
Подробнее про нормализацию можно почитать здесь, действительно понятно написано.
Для сегодняшнего примера мы используем такую формулу нормализации:
Функции нормализации, используя builtin-функции и средства numpy продемонстрированы ниже:
В этот раз объединим тесты в один цикл:
И создадим обычный график:
«Домашнее задание». Скорее всего, Вы открыли эту статью, поскольку интересуетесь языком программирования Python. Я предлагаю Вам попрактиковаться в визуализации данных.
Ладно, вернёмся к нормализации. Мы получаем такой график зависимости:
Результат почти такой же, как и с гиперболическим тангенсом. Вы можете также проанализировать другие функции или операции, чтобы найти слабые места NumPy.
Заключение NumPy vs Python
Цель этой статьи не в том, чтобы доказать очевидное. Я имел цель продемонстрировать как много получает пользователь, который знаком с NumPy. Фрагменты кода, продемонстрированные в статье дают начало бесконечному миру исследования вычислений с помощью различных инструментов, в котором Вы можете принять участие.
Весь код можно найти по ссылке в виде документа Jupyter Notebook.
Также рекомендую прочитать статью Анализ данных с pandas
Также заходите на мой YouTube-канал, где я обучают программированию на C#, а также рассказываю об общих вопросах программирования.