соответствие кодов и чисел в числовой системе эвм со знаком
Общие принципы представления информации. Числовая система ЭВМ
При работе с информацией возникает необходимость преобразования исходного представления информации, удобного для восприятия человеком, к представлению, удобному для хранения, передачи и обработки и наоборот. Такие преобразования называются кодированием и декодированием соответственно. Перечислим несколько известных систем кодирования:
Код Брайля (азбука для слепых): ;
Код морской сигнализации (морская флажковая азбука);
Двоичное кодирование: данные кодируются последовательностью 0 и 1.
С течением времени начали появляться по-настоящему сложные шифры. Один из них, употребляемый и поныне, связан с именем ученого аббата из Вюрцбурга Тритемиуса.
Клод Шеннон, ученый, заложивший основы теории информации, показал, как можно построить криптограмму, которая не поддается никакой расшифровке, если, конечно, не известен способ ее составления.
Коды, использующие два различных элементарных сигнала, называются двоичными. Удобно бывает, отвлекаясь от их физической природы, обозначать эти два сигнала символами 0 и 1. Тогда кодовые слова можно представлять как последовательности из нулей и единиц.
Последовательность битов, рассматриваемых аппаратной частью ЭВМ как единое целое, называется машинным словом.
Числовая система ЭВМ. Целые числа без знака и со знаком.
Введем основные понятия на примере 4-х битовых машинных слов. Сразу оговоримся, что такой размер слов практического интереса не представляет, однако основные закономерности сохраняют силу для машинных слов любого размера.
При последовательном увеличении 4-х битового слова 0000 на 0001 наступает ситуация, когда слово станет равным 1111 (1510). Если теперь к этому слову будет прибавлена 0001, то получим 0000, т.е. неверный результат (15+1=0) и исходное состояние. Это произошло потому, что слово памяти может состоять только из конечного числа битов. Таким образом, числовая система ЭВМ является конечной и цикличной.
Если знаковый бит = 0, то значение числа легко вычисляется (3 бита младших разрядов интерпретируются как двоичный код десятичного числа). Если знаковый бит = 1, то для оценки отрицательного числа нужно:
выполнить операцию инвертирования;
к полученному результату прибавить единицу.
3. Определите, какие отрицательные числа закодированы в словах 1011; 1100; 1001?
Индикаторы переноса и переполнения
Рассмотрим неверный арифметический результат, который возникает из-за конечной числовой системы ЭВМ.
В числовой системе без знака это будет: 1111+0001 = 0000 (15+1 = 0) возникает перенос единицы из знакового бита.
Итак, обработка числовой информации в процессоре зависит от длины машинного слова, при этом старший бит машинного слова является знаковым. Представление целых чисел в памяти ЭВМ зависит от того, сколько байт памяти отводится под целое число. Если целое число занимает 2 байта, тогда схему хранения целых чисел можно представить следующим образом:
Диапазон изменения целых чисел, которые занимают:
Отрицательные целые числа представляются в дополнительном коде (посредством операции дополнения до 2-х). Например, для 16-ти битового слова число «- 5» будет иметь код:
1111111111111011 (0000000000000101(+5) 1111111111111010 +00000000000000001 1111111111111011)
Представление вещественных чисел
Примеры. а) 372,95 = 0,37295103
б) 11010,1101 = 0,11010110125
Порядок определяет, насколько разрядов необходимо осуществить сдвиг относительно запятой. Это так называемые числа с плавающей запятой.
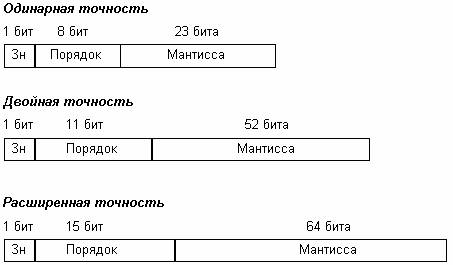
В памяти ЭВМ вещественные числа, приведенные к нормализованной форме, хранятся следующим образом. Для 32-х битового слова:
Порядок числа равен 128, а не 127, т.к. следует иметь в виду, что хотя для мантиссы отведены 23 разряда для одинарной точности и 55 разрядов для чисел двойной точности, в операциях участвуют 24 и 56 разрядов, т.е. имеет место скрытый разряд, который при аппаратном выполнении операций автоматически восстанавливается. Порядок числа учитывает скрытый старший разряд мантиссы.
Т.к. мантисса вещественного числа не может содержать более 7 десятичных цифр (ее мах = 8388607), компьютер при вычислениях отбрасывает лишние цифры в мантиссе, поэтому все вычисления с вещественными числами ЭВМ всегда выполняет приближенно, или с ошибкой. При более точных расчетах используются вычисления с двойной точностью. Нормализованные числа двойной точности занимают в два раза больше памяти (64 бита), под мантиссу при этом отводится 64-9 = 55 бит. В результате мантисса содержит 15 десятичных цифр. Точность расчетов возрастает в два раза.
Конспект по основам теории информации «Представление целых чисел в памяти ЭВМ»
Представление целых чисел в памяти ЭВМ.
Все числовые данные хранятся в ЭВМ в двоичном виде, т.е. в виде последовательности нулей и единиц, однако формы хранения целых и действительных чисел различны.
Для представления чисел в памяти ЭВМ используются два формата:
1. формат с фиксированной точкой (запятой) целые числа;
2. формат с плавающей точкой (запятой) вещественные числа.
Память ЭВМ состоит из ячеек. Каждая ячейка имеет определенную одинаковую для всех ячеек разрядность.
В схеме представлена восьмиразрядная память размером 1 Мбт.
Поэтому множество целых чисел, которое можно хранить и использовать в памяти ЭВМ, ограничено. Диапазон допустимых значений целых чисел зависит от размера ячеек памяти, используемых для их хранения.
Для целых чисел существуют два их представления в памяти ЭВМ:
В К-разрядной ячейке может храниться 2 к различных значений целых чисел.
Диапазон значений целых беззнаковых чисел (только положительные): от 0 до 2 к – 1.
Для 16-разрядной ячейки: от 0 до 65535.
Для 8-разрядной ячейки: от 0 до 255.
Нахождение прямого кода.
Чтобы получить внутреннее представление целого положительного числа N (прямой код), хранящегося в К-разрядной ячейке, необходимо:
1. перевести число N в двоичную систему счисления;
2. полученный результат дополнить слева незначащими нулями до К разрядов.
Пример 1. Получить внутреннее представление целого числа 1607 в 2-х байтовой ячейке.
Внутреннее представление этого числа будет:
0000 0110 0100 0111.
Шестнадцатеричная форма внутреннего представления числа: 0647.
Нахождение дополнительного кода.
Для представления целого отрицательного числа используется дополнительный код.
Получение дополнительного кода:
1. получить внутреннее представление положительного числа N (прямой код);
2. получить обратный код этого числа заменой 0 на 1 или 1 на 0 (обратный код);
3. к полученному числу прибавить 1.
Положительное число в прямом, обратном и дополнительном кодах не меняют свое изображение.
Использование дополнительного кода позволяет заменить операцию вычитания на операцию сложения.
Процессору достаточно уметь лишь складывать числа.
Старший, К-й разряд во внутреннем представлении любого положительного числа равен 0, отрицательного числа равен 1. Поэтому этот разряд называется знаковым разрядом.
1. Внутреннее представление положительного числа: 000 0110 0100 0111;
2. Обратный код: 1111 1001 1011 1000;
16-ричная форма: F9B9.
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс профессиональной переподготовки
Информатика: теория и методика преподавания в образовательной организации
Курс профессиональной переподготовки
Математика и информатика: теория и методика преподавания в образовательной организации
Онлайн-конференция для учителей, репетиторов и родителей
Формирование математических способностей у детей с разными образовательными потребностями с помощью ментальной арифметики и других современных методик
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Международная дистанционная олимпиада Осень 2021
Похожие материалы
Рабочая программа Внеурочной деятельности по направлению: общеинтеллектуальное развитие «В мире мультимедиа»
Рабочая программа по информатике курса «Программирование»
Рабочая программа. Информатика 10-11
Рабочая программа. Информатика 7-9
Научная статья «Современные подходы к понятию конструктивная деятельность обучающихся
Рабочая программа «Основы Интернета»
Не нашли то что искали?
Воспользуйтесь поиском по нашей базе из
5202306 материалов.
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Рособрнадзор рассчитывает, что экспресс-тесты на ковид в школах помогут избежать удаленки
Время чтения: 1 минута
В Госдуму внесли проект о горячем питании для учеников средних классов
Время чтения: 2 минуты
Рособрнадзор проведет исследование качества образования в школах
Время чтения: 2 минуты
В Москве подписан Меморандум о развитии и поддержке классного руководства
Время чтения: 1 минута
Рособрнадзор оставил за регионами решение о дополнительных школьных каникулах
Время чтения: 1 минута
Путин призвал наполнить аграрное образование современным содержанием
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Представление чисел в компьютере
После того, как мы узнали об основных единицах для измерения информации необходимо разобраться с тем, как в ЭВМ хранятся различные типы данных. В этой статье мы поговорим про представление чисел в компьютере.
Основные понятия и положения
Прежде чем начать разбираться в теме, следует понимать, что все ЭВМ, на данный момент времени, работают с двоичной системой счисления. Это значит, что и вся информация (звуковая, графическая или текстовая) хранится в памяти ПК в виде последовательностей нулей и единиц.
Схематично компьютерная память выглядит так, как показано на схеме ниже:
Как видно из рисунка внутренняя память представляет собой разряды, каждый из которых содержит один бит информации (0 или 1). А восемь битовых кластеров образуют один байт (машинное слово).
Машинное слово – минимально адресуемая ячейка памяти, которую за раз можно обработать командой процессора. То есть минимально процессор может обработать один байт.
Отсюда также вытекает правило, что данные в компьютере представляются дискретно (отдельно). В качестве примера приведем изображение на мониторе. Оно состоит из точек (пикселей). Цвет же каждой точки задается последовательностью из 0 и 1.
Представление чисел в компьютере
Существует несколько вариантов для отображения чисел в ЭВМ, и зависят они от формата числа.
Представление целых чисел в ЭВМ
Для представления целых чисел, в вычислительных машинах существует несколько способов, которые используют 8,16, 24 или 32 разряда памяти (1, 2, 3 и 4 байта).
Первым способом является беззнаковое представление. С его помощью представляются только целые положительные величины, которые не участвуют в арифметических операциях и выступают в роли констант (дата, время и т.д.).
Чтобы представить число в беззнаковой форме необходимо перевести его в двоичную систему счисления и дополнить с начала нулями до нужной разрядности (дополняем до 1,2,3 или 4 байт).
Также следует отметить, что есть ограничения на количество чисел, которые можно представить в n разрядной ячейке. Для беззнаковых величин оно составляет \( 2^n \).
Пример: Перевести 54 в беззнаковый формат.
Находим представление 54 в бинарной системе счисления:
\( 1) \ 54:2 \ = \ 27 \ | \ Остаток \ 0 \)
\( 2) \ 27:2 \ = \ 13 \ | \ Остаток \ 1 \)
\( 3) \ 13:2 \ = \ 6 \ | \ Остаток \ 1 \)
\( 4) \ 6:2 \ = \ 3 \ | \ Остаток \ 0 \)
\( 5) \ 3:2 \ = \ 1 \ | \ Остаток \ 1 \)
Итого \( 54_ <10>\) равняется \( 110110_ <2>\).
Дополняем результат до одной из стандартных разрядностей (8 бит) = 00110110.
Ответ: 00110110.
Для представления чисел, которые участвуют в вычислительных операциях, используется представление со знаком. В такой форме записи старший разряд всегда отводится под знак (0 для положительных чисел и 1 для отрицательных).
В случае со знаковым представлением также существуют ограничения. Так как один разряд отводится под знак, то в n-разрядную ячейку можно записать \( (2^
Также следует отметить следующую особенность — все отрицательные значения в компьютере хранятся в обратном или дополнительном коде, а положительные в прямом.
Для того чтобы перевести число в обратный и дополнительный код вам надо:
Почему же для хранения отрицательных чисел используют обратный или дополнительный код? Это позволяет изменить операцию вычитания на операцию сложения. В противном случае компьютеру бы каждый раз приходилось выяснять, где положительная величина, а где отрицательная и после этого сравнивать их модули, для определения конечного знака, что очень сильно усложняло бы весь алгоритм.
Представление вещественных чисел
Всего существует два способа для представления множества вещественных значений – естественная или экспоненциальная форма.
В жизни мы пользуемся естественной формой. Так число 42,6 мы можем записать несколькими способами. Например:
В компьютере же используется экспоненциальная форма записи. Выглядит она так:
Здесь m – мантисса, которая представляет собой правильную дробь (в правильных дробях числитель меньше знаменателя).
q – система счисления, в которой представлено число.
P – порядок.
В ЭВМ отводится один разряд под знак мантиссы, один под знак порядка и различное число бит под саму мантиссу и порядок. Данный формат записи называется «С плавающей запятой».
Чем больше бит отводится под мантиссу, тем точнее представляемая величина, чем больше ячеек отводится под порядок, тем шире диапазон от наименьшего числа, до наибольшего числа, представляемого в компьютере при заданном формате.
Так как компьютерная память величина дискретная и конечная, то и множество вещественных чисел, с которым работает ЭВМ также конечно.
Видео
Заключение
Вот мы и разобрались с представлением чисел в компьютере и информатике. Краткий материал из данной статьи вы можете использовать для своей онлайн-презентации. При возникновении вопросов оставляйте их в комментариях.
Представление чисел в ЭВМ
Целые числа
Для числа +1101 :
| Прямой код | Обратный код | Дополнительный код |
| 0,0001101 | 0,0001101 | 0,0001101 |
Вещественные числа (числа с плавающей точкой)
0.15625 = 001012
446.15625 = 110111110,001012 = 1,1011111000101*2 8
Знак S = 0
Порядок P = 8 + 1023 = 103110 = 100000001112
Мантисса: 1011111000101
Для числа с двойной точностью мантисса занимает 52 разряда. Добавляем нули.
Мантисса: 1011 1110 0010 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000
Запишем число:
0 10000000111 1011 1110 0010 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000
В шестнадцатеричной системе счисления: 407BE2800000000016
455,375 = 111000111,01102 = 1,110001110110*2 8 2
Дан код величины типа Double. Преобразуйте его число.
а) 408B894000000000;
Представим в двоичном коде:
010000001000 1011 1000 1001 0100 0000 0000 0000 0000 0000 0000 0000 0000 0000
где
S = 0 (положительное число)
P = 100000010002 = 1032 – 1023 = 9
M = 10111000100101
N = 1,10111000100101
С учетом P = 9, N = 1101110001,00101
1101110001 = 2 9 *1 + 2 8 *1 + 2 7 *0 + 2 6 *1 + 2 5 *1 + 2 4 *1 + 2 3 *0 + 2 2 *0+ 2 1 *0 + 2 0 *1 = 512 + 256 + 0 + 64 + 32 + 16 + 0 + 0 + 0 + 1 = 881
б) C089930000000000.
Представим в двоичном коде:
1 10000001000 100110010011000000000000000000000000 0000 0000 0000 0000
где
S = 1 (отрицательное число)
P = 100000010002 = 1032 – 1023 = 9
M = 100110010011
N =1,100110010011
С учетом P = 9, N = 1100110010,011
1100110010 = 2 9 *1 + 2 8 *1 + 2 7 *0 + 2 6 *0 + 2 5 *1 + 2 4 *1 + 2 3 *0 + 2 2 *0 + 2 1 *1 + 2 0 *0 = 512 + 256 + 0 + 0 + 32 + 16 + 0 + 0 + 2 + 0 = 818
Представление числовых данных в памяти ЭВМ
Для представления информации в памяти ЭВМ (как числовой, так и не числовой) используется двоичный способ кодирования.
Кодирование символов
Для кодирования символов достаточно одного байта. При этом можно представить 256 символов (с десятичными кодами от 0 до 255). Набор символов персональных ЭВМ, совместимых с IBM PC, чаще всего является расширением кода ASCII (American Standard Code for Information Interchange стандартный американский код для обмена информацией). В настоящее время используются и двухбайтовые предсталения символов.
Двоично-десятичное кодирование
В некоторых случаях при представлении чисел в памяти ЭВМ используется смешанная двоично-десятичная «система счисления», где для хранения каждого десятичного знака нужен полубайт (4 бита) и десятичные цифры от 0 до 9 представляются соответствующими двоичными числами от 0000 до 1001. Например, упакованный десятичный формат, предназначенный для хранения целых чисел с 18-ю значащими цифрами и занимающий в памяти 10 байт (старший из которых знаковый), использует именно этот вариант.
Представление целых чисел в дополнительном коде
Вообще, разряды нумеруются справа налево, начиная с 0. Ниже показана нумерация бит в двухбайтовом машинном слове.
| 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
Дополнительный код целого отрицательного числа может быть получен по следующему алгоритму:
При получении числа по его дополнительному коду прежде всего необходимо определить его знак. Если число окажется положительным, то просто перевести его код в десятичную систему счисления. В случае отрицательного числа необходимо выполнить следующий алгоритм:
Примеры. Запишем числа, соответствующие дополнительным кодам:
Кодирование вещественных чисел
Несколько иной способ применяется для представления в памяти персонального компьютера действительных чисел. Рассмотрим представление величин с плавающей точкой.
Покажем преобразование действительного числа для представления его в памяти ЭВМ на примере величины типа Double.
Как видно из таблицы, величина это типа занимает в памяти 8 байт. На рисунке ниже показано, как здесь представлены поля мантиссы и порядка (нумерация битов осуществляется справа налево):
| S | Смещенный порядок | Мантисса |
| 63 | 62..52 | 51..0 |
Таким образом, из вышесказанного вытекает следующий алгоритм для получения представления действительного числа в памяти ЭВМ:
Очевидно, что более компактно полученный код стоит записать следующим образом: C073850000000000(16).
Другой пример иллюстрирует обратный переход от кода действительного числа к самому числу.