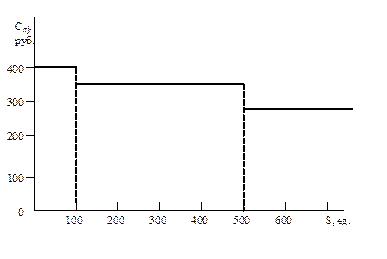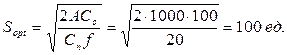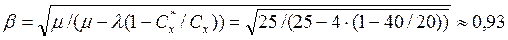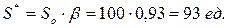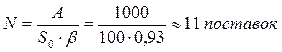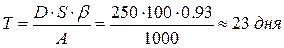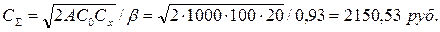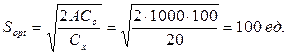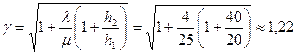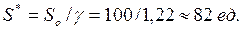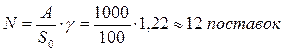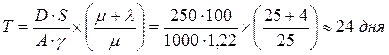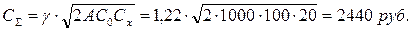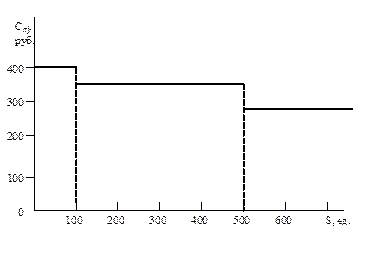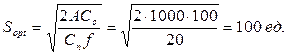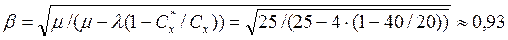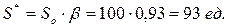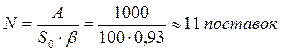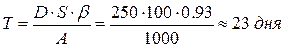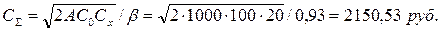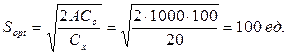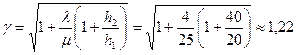Скидки учитываемые в модифицированных моделях eoq
Оптимальная партия поставки, EOQ-модель | Economic Order Quantity
Основной целью управления запасами, как одной из составляющих рабочего капитала, является минимизация совокупных расходов на их покупку, доставку и складское хранение. При этом расходы на доставку и хранение демонстрируют разнонаправленное поведение. С одной стороны, увеличение партии поставки приводит к снижению расходов на доставку в расчете на единицу запасов, а, с другой стороны, это приводит к росту складских расходов на единицу запасов. Для решения этой задачи Уилсоном (англ. R. H. Wilson) была разработана методика расчета оптимальной партии поставки (англ. Economic Order Quantity, EOQ), известная также как EOQ-модель или формула Уилсона.
Исходные положения EOQ-модели
Практическое применение EOQ-модели предполагает ряд ограничений, которые должны быть соблюдены при расчете оптимальной партии поставки:
1. Количество потребляемых запасов или закупаемых товаров заранее известно, а их потребление осуществляется равномерно в течение всего планируемого периода.
2. Стоимость организации заказа и стоимость одной единицы запасов остаются постоянными в течение всего планируемого периода.
3. Время поставки является фиксированным.
4. Замена отбракованных единиц осуществляется мгновенно.
5. Минимальный остаток запасов равен 0.
Расчет оптимальной партии поставки
В основе EOQ-модели лежит функция совокупных расходов (TC), которая отражает расходы на приобретение, доставку и хранение запасов.
p – цена покупки или себестоимость производства единицы запасов;
D – годовая потребность в запасах;
K – стоимость организации заказа (погрузка, разгрузка, упаковка, транспортные расходы);
Q – объем партии поставки.
H – стоимость хранения 1 единицы запасов в течение года (стоимость капитала, складские расходы, страховка и т.п.).
Для того чтобы рассчитать размер оптимальной партии поставки необходимо продифференцировать функцию совокупных расходов относительно переменной Q и приравнять к 0.
Решив полученное уравнение относительно переменной Q, мы получим оптимальную партию поставки (EOQ).
Графически это можно представить следующим образом:
Другими словами, оптимальная партия поставки представляет собой такой объем (Q), при котором значение функции совокупных расходов (TC) будет минимальным.
Пример. Годовая потребность компании по производству строительных материалов в цементе составляет 50000 т по цене 500 у.е. за тонну. При этом стоимость организации одной поставки составляет 350 у.е., а стоимость хранения 1 т цемента в течение года 2 у.е. В этом случае размер оптимальной партии поставки составит 2958 т.
В этом случае количество поставок за год составит 16,9 (50000/2958). Дробная часть 0,9 означает, что последняя 17-ая поставка будет выработана на 90%, а оставшиеся 10% перейдут остатком на следующий год.
Подставив оптимальную партию поставки в функцию совокупных расходов мы получим 25008874 у.е.
TC = 500*50000 + 50000*350/2958 + 2*2958/2 = 25008874 у.е.
При любом другом размере партии поставки сумма совокупных расходов будет выше. Например, для 3000 т она составит 25008833 у.е., а для 2900 т 25008934 у.е.
TC = 500*50000 + 50000*350/3000 + 2*3000/2 = 25008833 у.е.
TC = 500*50000 + 50000*350/2900 + 2*2900/2 = 25008934 у.е.
Графически потребление запасов можно представить следующим образом, при условии, что их остаток на начало года равен оптимальной партии поставки.
Учитывая исходные предположения EOQ-модели о равномерном потреблении запасов оптимальная партия поставки будет вырабатываться до нулевого остатка при условии, что в этот момент будет доставлена следующая партия.
Учет скидок в модели EOQ
При покупке партий товара большинство фирм дает скидки, величина которых зависит от размера партии (S). Среди различного вида скидок в управлении запасами наиболее часто используется так называемые оптовые скидки. Применение оптовых скидок означает, что цена единицы продукции Спj зависит от объема закупаемой партии Sj, при этом соблюдается правило, чем больше Sj, тем меньше цена Спj. Уменьшение цены представляется, как правило, в виде дискретной зависимости (см. рис. 5.2). На рис.5.2 показана ситуация, когда при величине заказа Sj≤100 ед. цена единицы товара Спо=400 руб.; при величине заказа S от 100 до 500 ед. цена единицы товара Сп1=350 руб.; наконец, при S больше 500 ед. цена Сп2=300 руб. Следовательно, заказывая 300 ед.продукции затраты на приобретение составят Ск=300х350=105 тыс. руб., а при заказе 600 ед. затраты Ск=180 тыс. руб.
Рис. 5.2. Зависимость оптовой цены продукции (Cпj) от
Иногда могут предоставляться дифференциальные скидки, при использовании которых скидки для каждой партии товара учитываются раздельно в каждом ценовом диапазоне. Здесь используется следующее правило. Если размер заказа колеблется от 1 до S1, например до 100 ед., то цена единицы изделия составляет Спо (допустим Спо=400 руб.); при размере заказа от S1+1 до S2 (от 101 до 500 ед.) цена снижается до Сп1 (Сп1=350 руб. как при оптовой скидке) и т.д. Но при дифференциальной скидке общие затраты при закупке партии в 300 ед. составят:
а средняя цена единицы изделия в этом случае составит:
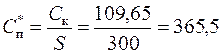
Для учета оптовых скидок наиболее часто используется дискретная зависимость Спj от Sj. При расчетах параметров модели EOQ с учетом оптовых скидок возможны различные ситуации.
Наиболее часто встречается первая ситуация, когда цена товара Спj изменяется, а затраты на хранение единицы продукции Сх, рассчитанные по формуле (5.3) в зависимости от Спj остаются постоянными.
Вторая ситуация, когда вместе с изменением цены Спj пропорционально изменяются и затраты на хранение Схj единицы продукции.
Третья ситуация при которой между изменениями цены Спj и затратами на хранение не наблюдается однозначной зависимости.
Рассмотрим последовательность расчета параметров модели EOQ для первой ситуации.
1. Зависимость суммарных затрат на приобретение, выполнение заказа и хранение записываются в виде:
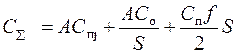
2. Выполним расчеты С∑ для различных значений S при следующих исходных данных: А=2000 ед., Со=800, f=0,2, цены для каждой единицы товара с учетом скидок приведены в табл. 5.1.
Изменение цены единицы продукции в зависимости от размера партии заказа
| Номер j | Размер партии поставки, ед. | Цена единицы товара со скидкой, Спj руб. |
| 1-100 101-500 501 и более |
Например, при S=50 ед. находим
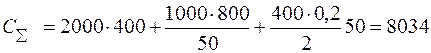
Результаты расчетов С∑ приведены в табл. 5.2.
Результаты расчета суммарных затрат с учетом скидки
| Цена единицы продукции Спj руб. | Размер заказа, S, ед. | Затраты на приобретение АСпj тыс. руб. | Затраты на выполнение заказа А∙Со/S, тыс. руб. | Затраты на хранение 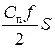 , тыс. руб. , тыс. руб. | Суммарные затраты С∑, тыс. руб. |
| 32,0 21,3 16,0 | 2,0 3,0 4,0 | 8034,0 8024,3 8020,0 | |||
| 15,8 10,7 8,0 6,4 4,0 3,6 3,2 | 4,0 6,0 8,0 10,0 16,0 18,0 20,0 | 7019,8 7016,7 7016,0 7016,4 7020,0 7021,6 7023,2 |
| Цена единицы продукции Спj руб. | Размер заказа, S, ед. | Затраты на приобретение АСпj тыс. руб. | Затраты на выполнение заказа А∙Со/S, тыс. руб. | Затраты на хранение 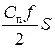 , тыс. руб. , тыс. руб. | Суммарные затраты С∑, тыс. руб. |
| 3,2 2,9 2,7 2,5 2,3 | 20,0 22,0 24,0 26,0 28,0 | 6023,2 6024,9 6026,7 6028,5 6030,3 |
3. Рассчитаем величину оптимальной партии заказа, формула (5.6), So=200 ед. и минимальные суммарные затраты, формула (5.9) С∑min=8000 руб. Однако, из анализа результатов, приведенных в табл.5.2, следует, что минимальные затраты С∑=6023,2 тыс. руб.
Таким образом, оптимальная партия заказа с учетом скидок Sо=501 ед.; соответственно число заказов в год N=4, а периодичность поставок Т=260/4=65 дней.
Следует отметить, что формула Харриса-Уилсона выведена с учетом большого числа допущений и ограничений [26, 29]:
— затраты на выполнение заказа Co, цена поставляемой продукции Сп и затраты на хранение единицы продукции в течение рассматриваемого периода постоянны;
— период между заказами (поставками) постоянный, т. е. Тз=const;
— заказ So выполняется полностью, мгновенно;
— интенсивность спроса ( 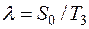
— емкость склада не ограничена;
— рассматриваются только текущие (регулярные) запасы, другие виды запасов (страховые, подготовительные, сезонные, транзитные и т. д.) не учитываются.
Модифицированные варианты модели EOQ
Можно выделить следующие основные модификации классической модели EOQ: модель производственного заказа (EPQ) – подразумевает немгновенную разгрузку с одновременным расходом запаса; модель экономичного размера партии (EBQ) – подразумевает постепенное пополнение запаса (без расхода) и последующий равномерный расход; модель текущего запаса с потерей требований при дефиците; модель текущего запаса с отложенным дефицитом; комбинированные модели.
Таблица 5.3
Варианты модифицированных моделей для определения оптимального размера заказа [27]
| Наименование модели | Графическое изображение | Примечание |
| 1. Производственного заказа EPQ (Economic Production Quantity) |  | Поступление 1; одновременное поступление и потребление 3; последующее потребление 2 |
Продолжение табл. 5.3
| Наименование модели | Графическое изображение | Примечание |
| 2. Экономичного размера партии EBQ (Economic Batch Quantity) | 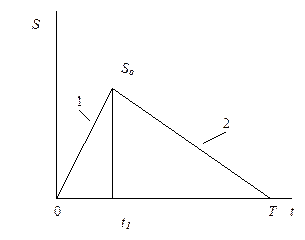 | Поступление 1 (без потребления); последующее потребление 2 |
| 3. Текущего запаса с отложенным дефицитом (I) | 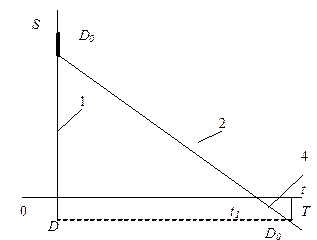 | После мгновенного поступления 1, сначала выполняется (мгновенно) отложенный спрос D0, затем этап потребления 2 и дефицита 4 |
| 4. Текущего запаса с потерей требований при дефиците (II) | 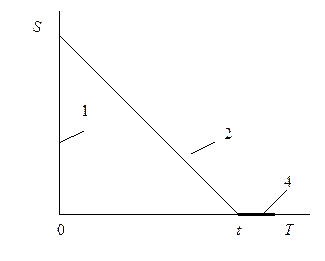 | После мгновенного поступления 1; этап потребления 2 и этап дефицита 4, когда требования не выполняются и не накапливаются |
Продолжение табл. 5.3
| Наименование модели | Графическое изображение | Примечание |
| 5. Экономичного размера партии с потерей требований при дефиците | 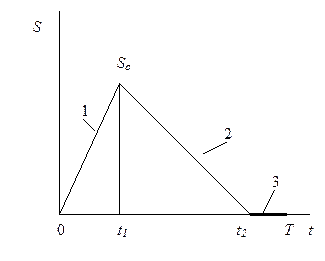 | Поступление 1 (без потребления); потребление 2; дефицит 3 (требования не выполняются и не накапливаются) |
| 6. Экономичного размера партии с дефицитом (отложенный спрос) | 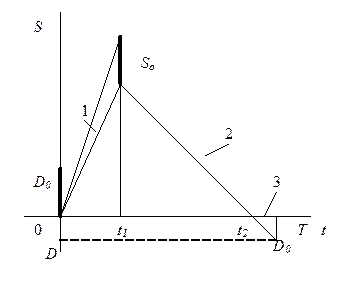 | Поступление 1 (с мгновенным выполнением отложенного спроса Dо в момент t=0); потребление 2, этап дефицита 3 (с накоплением требований). |
| 7. Производственного заказа с дефицитом (отложенный спрос) | 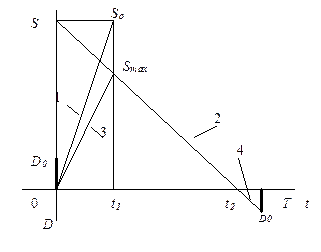 | Поступление 1 (с мгновенным выполнением отложенного спроса Dо в момент t=0); поступление с одновременным потреблением 3; потребление 2; этап дефицита 4 (с накоплением требований) |
| Наименование модели | Графическое изображение | Примечание |
| 8. Производственного заказа с потерей требований при дефиците | 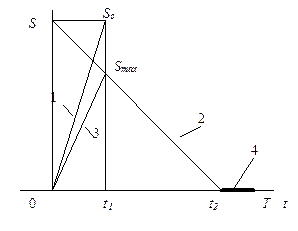 | Поступление 1; поступление с одновременным потреблением 3; потребление 2, этап дефицита (с потерей требований) |
Откорректированные зависимости для расчета параметров модели EPQ c немгновенной разгрузкой [27, 32]
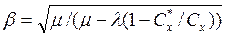
Пример 5.3[27]:
— потребность в заказываемом продукте А=1000 ед. в год;
— затраты на выполнение одного заказа Со=100 руб.;
— затраты на хранение единицы продукции (на складе) СХ=20 руб./ед. год;
— количество рабочих дней в году D=250 дней;
— интенсивность пополнения запасов на склад μ =25 ед./день;
— интенсивность расхода запаса со склада λ=4 ед./день;
— затраты на хранение доставленной продукции вне склада С * Х =40 руб./ед. год
Рассчитаем S0, для этого воспользуемся формулой (5.6):
По формуле (5.18) найдем значение поправочного коэффициента β:
Теперь можно определить параметры модели EPQ и рассчитать суммарные минимальные затраты:
— оптимальная партия поставки:
— оптимальное количество поставок:
— оптимальная периодичность поставок:
— суммарные минимальные затраты:
Откорректированные зависимости для расчета показателей модели экономичного размера партии (EBQ) [27, 32]
Корректирующий коэффициент 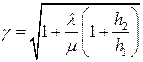
где h2 – затраты на хранение в транспортном средстве;
h1 – затраты на хранение на складе;
Пример 5.4:
Пусть нам известно следующее:
— потребность в заказываемом продукте (А)=1000 ед. в год;
— затраты на выполнение одного заказа (Со)=100 руб.;
— затраты на хранение единицы продукции на складе (h1 или Сх) =20 руб./ед. год;
— затраты на хранение доставленной продукции в транспортном средстве (h2) = 40 руб./ед. год
— количество рабочих дней в году (D)=250 дней;
— интенсивность пополнения запасов на склад (μ)=25 ед./день;
— интенсивность расхода запаса со склада (λ) = 4 ед./день;
По формуле (5.19) найдем значение поправочного коэффициента γ:
Теперь рассчитаем параметры модели EBQ и определим суммарные минимальные затраты:
— оптимальная партия поставки:
— оптимальное количество поставок:
— оптимальная периодичность поставок:
— суммарные минимальные затраты:
Дата добавления: 2016-01-07 ; просмотров: 1813 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Учет скидок в модели EOQ



При покупке партий товара большинство фирм дает скидки, величина которых зависит от размера партии (S). Среди различного вида скидок в управлении запасами наиболее часто используется так называемые оптовые скидки. Применение оптовых скидок означает, что цена единицы продукции Спj зависит от объема закупаемой партии Sj, при этом соблюдается правило, чем больше Sj, тем меньше цена Спj. Уменьшение цены представляется, как правило, в виде дискретной зависимости (см. рис. 5.2). На рис.5.2 показана ситуация, когда при величине заказа Sj≤100 ед. цена единицы товара Спо=400 руб.; при величине заказа S от 100 до 500 ед. цена единицы товара Сп1=350 руб.; наконец, при S больше 500 ед. цена Сп2=300 руб. Следовательно, заказывая 300 ед.продукции затраты на приобретение составят Ск=300х350=105 тыс. руб., а при заказе 600 ед. затраты Ск=180 тыс. руб.
Рис. 5.2. Зависимость оптовой цены продукции (Cпj) от
Иногда могут предоставляться дифференциальные скидки, при использовании которых скидки для каждой партии товара учитываются раздельно в каждом ценовом диапазоне. Здесь используется следующее правило. Если размер заказа колеблется от 1 до S1, например до 100 ед., то цена единицы изделия составляет Спо (допустим Спо=400 руб.); при размере заказа от S1+1 до S2 (от 101 до 500 ед.) цена снижается до Сп1 (Сп1=350 руб. как при оптовой скидке) и т.д. Но при дифференциальной скидке общие затраты при закупке партии в 300 ед. составят:
а средняя цена единицы изделия в этом случае составит:
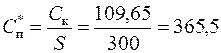
Для учета оптовых скидок наиболее часто используется дискретная зависимость Спj от Sj. При расчетах параметров модели EOQ с учетом оптовых скидок возможны различные ситуации.
Наиболее часто встречается первая ситуация, когда цена товара Спj изменяется, а затраты на хранение единицы продукции Сх, рассчитанные по формуле (5.3) в зависимости от Спj остаются постоянными.
Вторая ситуация, когда вместе с изменением цены Спj пропорционально изменяются и затраты на хранение Схj единицы продукции.
Третья ситуация при которой между изменениями цены Спj и затратами на хранение не наблюдается однозначной зависимости.
Рассмотрим последовательность расчета параметров модели EOQ для первой ситуации.
1. Зависимость суммарных затрат на приобретение, выполнение заказа и хранение записываются в виде:
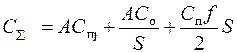
2. Выполним расчеты С∑ для различных значений S при следующих исходных данных: А=2000 ед., Со=800, f=0,2, цены для каждой единицы товара с учетом скидок приведены в табл. 5.1.
Изменение цены единицы продукции в зависимости от размера партии заказа
| Номер j | Размер партии поставки, ед. | Цена единицы товара со скидкой, Спj руб. |
| 1-100 101-500 501 и более |
Например, при S=50 ед. находим
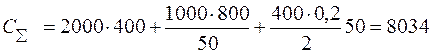
Результаты расчетов С∑ приведены в табл. 5.2.
Результаты расчета суммарных затрат с учетом скидки
| Цена единицы продукции Спj руб. | Размер заказа, S, ед. | Затраты на приобретение АСпj тыс. руб. | Затраты на выполнение заказа А∙Со/S, тыс. руб. | Затраты на хранение 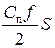 , тыс. руб. , тыс. руб. | Суммарные затраты С∑, тыс. руб. |
| 32,0 21,3 16,0 | 2,0 3,0 4,0 | 8034,0 8024,3 8020,0 | |||
| 15,8 10,7 8,0 6,4 4,0 3,6 3,2 | 4,0 6,0 8,0 10,0 16,0 18,0 20,0 | 7019,8 7016,7 7016,0 7016,4 7020,0 7021,6 7023,2 |
| Цена единицы продукции Спj руб. | Размер заказа, S, ед. | Затраты на приобретение АСпj тыс. руб. | Затраты на выполнение заказа А∙Со/S, тыс. руб. | Затраты на хранение 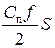 , тыс. руб. , тыс. руб. | Суммарные затраты С∑, тыс. руб. |
| 3,2 2,9 2,7 2,5 2,3 | 20,0 22,0 24,0 26,0 28,0 | 6023,2 6024,9 6026,7 6028,5 6030,3 |
3. Рассчитаем величину оптимальной партии заказа, формула (5.6), So=200 ед. и минимальные суммарные затраты, формула (5.9) С∑min=8000 руб. Однако, из анализа результатов, приведенных в табл.5.2, следует, что минимальные затраты С∑=6023,2 тыс. руб.
Таким образом, оптимальная партия заказа с учетом скидок Sо=501 ед.; соответственно число заказов в год N=4, а периодичность поставок Т=260/4=65 дней.
Следует отметить, что формула Харриса-Уилсона выведена с учетом большого числа допущений и ограничений [26, 29]:
— затраты на выполнение заказа Co, цена поставляемой продукции Сп и затраты на хранение единицы продукции в течение рассматриваемого периода постоянны;
— период между заказами (поставками) постоянный, т. е. Тз=const;
— заказ So выполняется полностью, мгновенно;
— интенсивность спроса ( 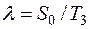
— емкость склада не ограничена;
— рассматриваются только текущие (регулярные) запасы, другие виды запасов (страховые, подготовительные, сезонные, транзитные и т. д.) не учитываются.
5.5. Модифицированные варианты модели EOQ
Можно выделить следующие основные модификации классической модели EOQ: модель производственного заказа (EPQ) – подразумевает немгновенную разгрузку с одновременным расходом запаса; модель экономичного размера партии (EBQ) – подразумевает постепенное пополнение запаса (без расхода) и последующий равномерный расход; модель текущего запаса с потерей требований при дефиците; модель текущего запаса с отложенным дефицитом; комбинированные модели.
Таблица 5.3
Варианты модифицированных моделей для определения оптимального размера заказа [27]
| Наименование модели | Графическое изображение | Примечание |
| 1. Производственного заказа EPQ (Economic Production Quantity) |  | Поступление 1; одновременное поступление и потребление 3; последующее потребление 2 |
Продолжение табл. 5.3
| Наименование модели | Графическое изображение | Примечание |
| 2. Экономичного размера партии EBQ (Economic Batch Quantity) | 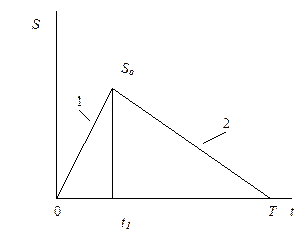 | Поступление 1 (без потребления); последующее потребление 2 |
| 3. Текущего запаса с отложенным дефицитом (I) | 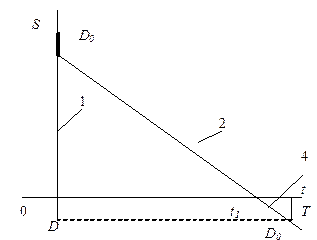 | После мгновенного поступления 1, сначала выполняется (мгновенно) отложенный спрос D0, затем этап потребления 2 и дефицита 4 |
| 4. Текущего запаса с потерей требований при дефиците (II) | 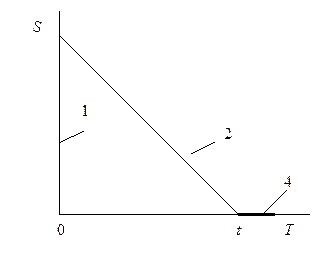 | После мгновенного поступления 1; этап потребления 2 и этап дефицита 4, когда требования не выполняются и не накапливаются |
Продолжение табл. 5.3
| Наименование модели | Графическое изображение | Примечание |
| 5. Экономичного размера партии с потерей требований при дефиците | 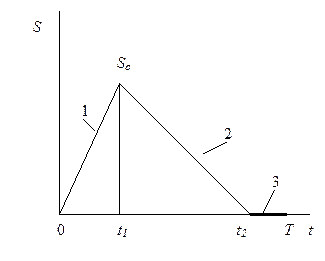 | Поступление 1 (без потребления); потребление 2; дефицит 3 (требования не выполняются и не накапливаются) |
| 6. Экономичного размера партии с дефицитом (отложенный спрос) | 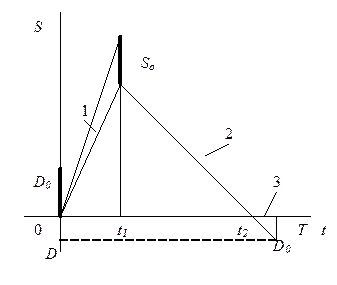 | Поступление 1 (с мгновенным выполнением отложенного спроса Dо в момент t=0); потребление 2, этап дефицита 3 (с накоплением требований). |
| 7. Производственного заказа с дефицитом (отложенный спрос) |  | Поступление 1 (с мгновенным выполнением отложенного спроса Dо в момент t=0); поступление с одновременным потреблением 3; потребление 2; этап дефицита 4 (с накоплением требований) |
| Наименование модели | Графическое изображение | Примечание |
| 8. Производственного заказа с потерей требований при дефиците | 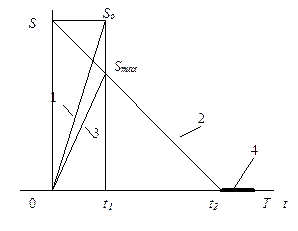 | Поступление 1; поступление с одновременным потреблением 3; потребление 2, этап дефицита (с потерей требований) |
Откорректированные зависимости для расчета параметров модели EPQ c немгновенной разгрузкой [27, 32]
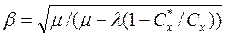
Пример 5.3[27]:
— потребность в заказываемом продукте А=1000 ед. в год;
— затраты на выполнение одного заказа Со=100 руб.;
— затраты на хранение единицы продукции (на складе) СХ=20 руб./ед. год;
— количество рабочих дней в году D=250 дней;
— интенсивность пополнения запасов на склад μ =25 ед./день;
— интенсивность расхода запаса со склада λ=4 ед./день;
— затраты на хранение доставленной продукции вне склада С * Х =40 руб./ед. год
Рассчитаем S0, для этого воспользуемся формулой (5.6):
По формуле (5.18) найдем значение поправочного коэффициента β:
Теперь можно определить параметры модели EPQ и рассчитать суммарные минимальные затраты:
— оптимальная партия поставки:
— оптимальное количество поставок:
— оптимальная периодичность поставок:
— суммарные минимальные затраты:
Откорректированные зависимости для расчета показателей модели экономичного размера партии (EBQ) [27, 32]
Корректирующий коэффициент 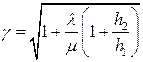
где h2 – затраты на хранение в транспортном средстве;
h1 – затраты на хранение на складе;
Пример 5.4:
Пусть нам известно следующее:
— потребность в заказываемом продукте (А)=1000 ед. в год;
— затраты на выполнение одного заказа (Со)=100 руб.;
— затраты на хранение единицы продукции на складе (h1 или Сх) =20 руб./ед. год;
— затраты на хранение доставленной продукции в транспортном средстве (h2) = 40 руб./ед. год
— количество рабочих дней в году (D)=250 дней;
— интенсивность пополнения запасов на склад (μ)=25 ед./день;
— интенсивность расхода запаса со склада (λ) = 4 ед./день;
По формуле (5.19) найдем значение поправочного коэффициента γ:
Теперь рассчитаем параметры модели EBQ и определим суммарные минимальные затраты: