равномерные и неравномерные коды достоинства и недостатки
Равномерные и неравномерные коды.
Дата добавления: 2015-08-14 ; просмотров: 33165 ; Нарушение авторских прав
Код называется равномерным (или кодом постоянной длины), если все его кодовые слова содержат одинаковое число букв (одинаковую длину слов). Соответственно, кодирование называется равномерным, если соответствующий ему код имеет постоянную длину. В настоящее время в информатике более употребительно равномерное кодирование, оно проще и более удобно. В компьютерах при кодировании информации в основном используются равномерные коды, соответствующие размерам компьютерных ячеек.
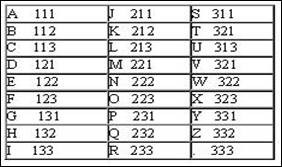
Другим интересным примером равномерного кода является код Трисиме, в котором знакам латинского алфавита ставятся в соответствие кодовые слова длины 3 над алфавитом из 3-х символов: <1, 2, 3>. Этот код представлен в следующей таблице :
Понятно, что код Трисиме не может кодировать более чем 3 3 =27 символов.
Число букв в алфавите кода называется основанием кода, а длина кодовых слов равномерного кода называется порядком кода. Коды с основанием 2, как уже говорилось, называются двоичными, а с основанием 3 – троичными, и так далее. Так код Бодо имеет основание 2, а порядок 5, а у кода Трисиме и основание, и порядок равны 3.
Код называется неравномерным (или кодом переменной длины), если его кодовые слова имеют разное число букв (неодинаковую длину слов). Соответственно, кодирование называется неравномерным, если соответствующий ему код неравномерный.
Типичным примером неравномерного кода является телеграфный код, который принято называть азбукой Морзе. На следующей таблице представлен код азбуки Морзе для русского алфавита:
| A | • − | И | • • | P | • − • | Ш | − − − − | • − − − − | − − − − • | |
| Б | − • • • | Й | • − − − | С | • • • | Щ | − − • − | • • − − − | − − − − − | |
| В | • − − | К | − • − | Т | − | Ъ | • − − • − • | • • • − − | Точка | • • • • • • |
| Г | − − • | Л | • − • • | У | • • − | Ь | − • • − | • • • • − | Запятая | • − • − • − |
| Д | − • • | М | − − | Ф | • • − • | Ы | − • − − | • • • • • | / | − • • − • |
| Е | • | H | − • | Х | • • • • | Э | • • − • • | − • • • • | ? | • • − − • • |
| Ж | • • • − | О | − − − | Ц | − • − • | Ю | • • − − | − − • • • | ! | − − • • − − |
| З | − − • • | П | • − − • | Ч | − − − • | Я | • − • − | − − − • • | @ | • − − • − • |
Американский изобретатель телеграфа Сэмюель Морзе разработал этот код в 1838 году для передачи телеграфных сообщений в виде последовательности электрических сигналов, передаваемых от одного телеграфного аппарата по проводам к другому телеграфному аппарату. Этот код был придуман Морзе задолго до научных исследований
 |
| СэмюэлМорзе (1791-1872) |
относительной частоты появления различных букв в текстах, но, тем не менее, Морзе при составлении кода использовал принцип частоты букв. Буквам, используемым чаще, им присвоены короткие кодовые комбинации, редко используемым буквам – длинные. Морзе оценил относительную частоту букв английского языка подсчетом литер в ячейках типографской наборной машины. Наиболее часто используемой букве «Е» (в английском языке) он присвоил наиболее короткий код «точка». Следующей по количеству литер букве он присвоил код несколько большей длительности и так далее.
При составлении азбуки Морзе для букв русского алфавита учет относительной частоты букв не производился, и это повысило его избыточность. Расчеты избыточности кода Морзе на основании проведенных исследований частоты появления букв показали, что для букв английского алфавита она составляет 19%, для букв русского алфавита 22%.
Преимущество у неравномерных кодов перед равномерными как раз и состоит в том, что сообщения можно передавать более экономным способом, так как часто передаваемые кодовые слова более короткие, а значит, кодовая последовательность может иметь меньшую длину, чем для равномерных кодов. Ниже это будет показано.
Но у неравномерных кодов есть серьезный недостаток по сравнению с равномерными кодами. У равномерных кодов кодовая последовательность всегда декодируется однозначно за счет того, что кодовые слова имеют одинаковую длину (кодовая последовательность легко делится на кодовые слова). Но не для всех неравномерных кодов достигается однозначность декодирования кодовых последовательностей. Мы уже видели это, пытаясь рассматривать азбуку Морзе как двоичный код.
Этот код неравномерный (кодовые слова разной длины).
Закодируем последовательность сообщений: s7s7. Имеем F(s7s7)=B=111111. Но эта последовательность может быть декодирована и по-другому, так как: B=F(s3s3s3)= F(s1s3s7)=F(s3s7s1)=F(s1s1s1s1s1s1s1s). Как видим, способов декодирования много (подсчитайте: сколько их?). Неоднозначно декодируется и следующая последовательность:
11011011 (а сколько здесь способов декодирования?). Очевидно, что такой код практически использовать нельзя. А если мы изменим код так, чтобы он стал равномерным, например, доопределим функцию F так:
то теперь никаких проблем с декодированием не будет.
ГДЗ по информатике 10 класс учебник Босова параграф 4
1. Приведите примеры процессов обработки информации, которые чаще всего вам приходится выполнять в жизни. Для каждого примера определите исходные данные, алгоритм (правила) обработки и получаемые результаты. К каким типам обработки информации относятся эти процессы?
2. Поясните суть понятий «кодирование», «код», «кодовая таблица».
Кодирование — это обработка информации, заключающаяся в её преобразовании в некоторую форму, удобную для хранения, передачи, обработки информации в дальнейшем.
Код — это система (список) условных обозначений (кодовых слов), используемых для представления информации.
3. Светодиодная панель содержит шесть излучающих элементов, каждый из которых может светиться или красным, или жёлтым, или зелёным цветом. Сколько различных сигналов можно передать с помощью панели (все излучающие элементы должны гореть, порядок цветов имеет значение)?
Итак, у нас получилось 6-значное число в 4-ричной системе счисления.
Таких чисел (различных сигналов, то есть комбинаций) может быть (это ответ):
4. Автомобильный номер состоит из нескольких букв (количество букв одинаковое во всех номерах), за которыми следуют три цифры. При этом используются 10 цифр и только 5 букв: А, В, С, D и F. Требуется не менее 100 тысяч различных номеров. Какое наименьшее количество букв должно быть в автомобильном номере?
5. Сколько существует различных последовательностей из 6 символов четырёхбуквенного алфавита <А, В, С, D>, которые содержат не менее двух букв А (т. е. две и более буквы А)?
Предлагаю найти количество всех последовательностей и вычесть из них те, в которых содержится менее двух букв А.
Всего последовательностей: 4^6 = 4096
Последовательностей без буквы А: 3^6 = 729
С одной буквой А: 6 * 3^5 = 1458
6. Сравните равномерные и неравномерные коды. Каковы их основные достоинства и недостатки?
Равномерные коды легче декодировать, но закодированные сообщения будут содержать больше символов. Сообщения, закодированные неравномерными кодами, будут короче, чем на равномерных кодах, но необходимо будет для кодирования сообщения проверять код на условие Фано, и закодированное сообщение сложнее раскодировать. Так же невозможно сразу посчитав количество символов, по сравнению с равномерными кодами.
7. Какие коды называют префиксными? Почему они так важны? В чём суть прямого и обратного условий Фано?
Код называется префиксным, если ни одна из его комбинаций не является префиксом другой комбинации того же кода. Часть кодовой комбинации, которая дополняет префикс до самой комбинации, называется суффиксом. Префиксные коды наглядно могут быть представлены с помощью кодовых деревьев. Если ни один узел кодового дерева не является вершиной данного кода, то он обладает свойствами префикса. Узлы дерева, которые не соединяются с другими, называются конечными. Комбинации, которые им соответствуют, являются кодовыми комбинациями префиксного кода.
8. Двоичные коды для 5 букв латинского алфавита представлены в таблице:
Из четырёх сообщений, закодированных этими кодами, только одно пришло без ошибки. Найдите его:
1) 110100000100110011;
2) 111010000010010011;
3) 110100001001100111;
4) 110110000100110010.
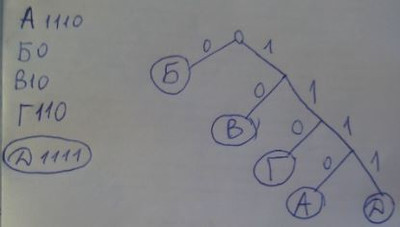
9. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. При этом используются следующие коды: А — 1110, Б — 0, В — 10, Г — 110. Каким кодовым словом может быть закодирована буква Д? Код должен удовлетворять свойству однозначного декодирования. Если можно использовать более одного кодового слова, укажите кратчайшее из них.
10. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный троичный код, позволяющий однозначно декодировать полученную троичную последовательность. Вот этот код: А — 0, Б — 11, В — 20, Г — 21, Д — 22. Можно ли сократить для одной из букв длину кодового слова так, чтобы закодированную последовательность по-прежнему можно было декодировать однозначно? Коды остальных букв меняться не должны.
11. Для передачи закодированных сообщений используется таблица кодовых слов из четырёх букв. Причем используются только буквы А, Р и У. Сколько различных кодовых слов может быть в такой таблице, если ни в одном слове нет трёх одинаковых букв, идущих подряд?
Различных слов длины 4, состоящих из букв А, Р и У, ровно 3 4 =81.
Выпишем все запрещённые слова. Сначала выпишем все те слова, в которых три одинаковых буквы подряд идут с позиции 1 по позицию 3:
АААА, АААР, АААУ
РРРА, РРРР, РРРУ
УУУА, УУУР, УУУУ
Теперь выпишем те, в которых одинаковые буквы стоят на позиции 2-4 (без учёта тех слов, в которых все буквы одинаковые, т.к. они были выписаны ранее)
РААА, УААА
Всего получилось 15 запрещённых слов, значит, разрешённых слов 81-15=66.
12. Методом половинного деления в последовательности чисел 061 087 154 180 208 230 290 345 367 389 456 478 523 567 590 612 требуется найти число 590. Опишите процесс поиска.
Просмотр 1. Работаем со всей последовательностью. Определяем центральный элемент (он подчёркнут):
061 087 154 180 208 230 290 345 367 389 456 478 523 567 590 612
Сравниваем искомый элемент с центральным.
По результатам сравнения отбрасываем левую часть последовательности.
Просмотр 2. Работаем с правой частью последовательности. Определяем центральный элемент (он подчёркнут):
367 389 456 478 523 567 590 612
Сравниваем искомый элемент с центральным.
По результатам сравнения отбрасываем левую часть последовательности.
Просмотр 3. Работаем с правой частью последовательности. Определяем центральный элемент (он подчёркнут):
Сравниваем искомый элемент с центральным.
Центральный элемент совпадает с искомым. Поиск завершён.
13. В Международном конкурсе по информатике «Бобёр» школьникам была предложена задача «Склад», подготовленная специалистами из Японии. Вот её условие.
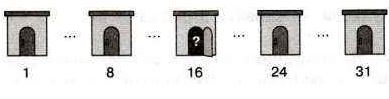
Плотник в Бобровой Деревне использует 31 склад, пронумерованный от 1 до 31. Однажды он забыл, сколько складов уже заполнил, но помнит, что заполнял их в порядке возрастания номеров.
Чтобы уменьшить количество открывания дверей, он действует следующим образом:
Сначала открывает склад со средним номером — склад № 16. Затем:
• если склад № 16 пуст, он решает искать первый незаполненный склад в промежутке от № 1 до № 15, открывает опять средний склад — склад № 8 — и повторяет процедуру;
• если склад № 16 заполнен, то нужный склад он ищет между № 17 и № 31, открывает средний склад — склад № 24 — и повторяет процедуру.
После всех действий плотник обнаружил, что заполнены были склады от № 1 до № 15 включительно. Сколько дверей ему пришлось открыть?
Решите эту задачу. Какой из рассмотренных нами методов поиска был использован героем этой задачи?
Двоичный поиск эффективно определяет положение искомого элемента (или его отсутствие) в упорядоченном наборе.
Это один из базовых и важных алгоритмов.
Если склады от №1 до №15 заполнены, то:
— когда плотник открывает склад №16, он оказывается пуст (1-ая открытая дверь);
— тогда плотник решает искать между №1 и №15, открывает склад №8, он оказывается заполнен (2-ая открытая дверь);
— теперь он ищет между №9 и №15, открывает склад №12 — он заполнен (3-ья открытая дверь);
— наконец он открывает последний склад № 15 (5-ая дверь).
Равномерные и неравномерные коды достоинства и недостатки
Здравствуйте! Меня зовут Александр Георгиевич. Я являюсь профессиональным репетитором в области информационных технологий, математике, баз данных и программирования.
Если у вас возникли затруднения с обработкой равномерного или неравномерного кода, то срочно записывайтесь ко мне на первый пробный урок, на которых мы с вами очень детально разберем все ваши вопросы и прорешаем большое количество различных тематических упражнений.
Чтобы гарантированно набрать на официальном экзамене ОГЭ или ЕГЭ по информатике высоченный балл берите сотовый телефон, дозванивайтесь до меня и задавайте любые интересующие вопросы.
Рекомендую использовать формат дистанционного обучения! Это выгодно, удобно и эффективно!
Что такое равномерный код и в каких случаях его применяют?
Допустим, вам требуется написать секретное письмо и отправить его своему другу. Вы – человек, проживающий на территории России, следовательно, использующий для написания слов буквы русского алфавита. И, вот, вы решаете закодировать ваше послание двоичным кодом, то есть вместо русских слов ваш друг получит набор цепочек, состоящий из нулей и единиц.
Но ваш соратник без особых проблем сможет провести дешифрацию вашего информационного сообщения, так как вы ему расскажете об алгоритме шифрации/дешифрации.
Символ
Равномерный код
Десятичное представление
Равномерный код – такой код, когда все символы какого-либо алфавита кодируются кодами одинаковой длины.
Что такое неравномерный код и в каких случаях его применяют?
Чтобы глубоко понять смысл неравномерного кодирования давайте представим, что вы работаете на продуктовом складе. Вы хотите оптимизировать свою работу и закодировать название каждого товара минимально возможным количеством бит.
На ум приходит вариант с равномерным кодом, то есть закодировать название каждого продукта информационным кодом одинаковой длины. Но в данном случае это не самый оптимальный вариант кодирования. Почему? Потому что один товар является наиболее популярным и востребованным, и вам, как кладовщику, приходится чаще с ним взаимодействовать.
Следует понять общий принцип неравномерного кода: суть его в том, чтобы кодировать наиболее часто используемые элементы как можно меньшим количеством бит, так как ими вы оперируете очень часто.
Неравномерный код – такой код, когда все элементы какого-либо множества кодируются кодом различной длины.
Данные четыре товара покупают огромными партиями и вы уже устали вести записи в базе данных постоянно вбивая названиях этих продуктов. Давайте применим следующее кодирование:
Итого, нам потребовалось два бита информации, чтобы закодировать в бинарном виде наиболее ходовых четыре товара.
А как поступить с наименее популярными товарами, например, муку и перец также достаточно часто покупают. В этом случае данные товары можно запрограммировать так:
Вы должны уловить общий принцип: чем наименее популярный товар, тем большим количеством бит он будет закодирован.
И все бы хорошо, но есть одна существенная проблема, возникающая при создании неравномерного кода, – проблема с однозначной дешифрацией. Для полного понимания данной проблемы вам следует познакомиться с условием Фано.
Равномерный код vs неравномерный код
Чтобы хорошо понимать в каких ситуациях стоит применять то или иное кодирование, вам нужно очень хорошо разобраться с частотой использования элементов, которые вы планируете закодировать. Если частота применения приблизительно равна у всех элементов, то смело применяйте равномерный код, в других случаях – неравномерный код.
А сейчас я вам предлагаю ознакомиться с мультимедийным решением, в котором я показываю, как правильно оперировать равномерным и неравномерным кодом.
Я хочу записаться к вам на индивидуальный урок по информатике и ИКТ
Если у вас остались какие-либо вопросы по рассматриваемой теме, то записывайтесь ко мне на первый пробный урок. Я репетитор-практик, следовательно, на своих уроках я уделяю максимум внимания решению заданий. Из теории лишь записываются самые базовые сведения: определения, тезисы, формулировки теорем и аксиом.
Специально для своих потенциальных клиентов я разработал стабильную многопараметрическую систему, состоящую из 144 вариантов нашего будущего взаимовыгодного сотрудничества. Даже самый взыскательный клиент сумеет выбрать вариант, полностью покрывающий его запросы.
Не откладывайте свое решение в долгий ящик. Я все-таки достаточно востребованный и квалифицированный репетитор, поэтому звоните прямо сейчас – количество ученических мест ограниченно!
Урок 7
Дискретная форма представления информации
Содержание урока
1.5.3. Универсальность двоичного кодирования. 1.5.4. Равномерные и неравномерные коды
1.5.3. Универсальность двоичного кодирования
1.5.4. Равномерные и неравномерные коды
1.5.3. Универсальность двоичного кодирования
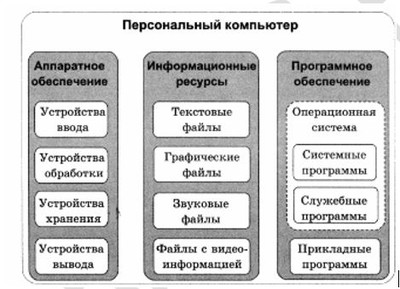
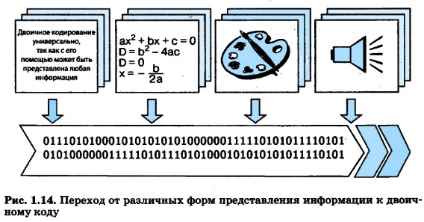
В начале этого параграфа вы узнали, что информация, представленная в непрерывной форме, может быть выражена с помощью символов некоторого естественного или формального языка. В свою очередь, символы произвольного алфавита могут быть преобразованы в двоичный код. Таким образом, с помощью двоичного кода может быть представлена любая информация на естественных и формальных языках, а также изображения и звуки (рис. 1.14). Это и означает универсальность двоичного кодирования.
Двоичные коды широко используются в компьютерной технике, требуя только двух состояний электронной схемы — «включено» (это соответствует цифре 1) и «выключено» (это соответствует цифре О).
Простота технической реализации — главное достоинство двоичного кодирования. Недостаток двоичного кодирования — большая длина получаемого кода.
1.5.4. Равномерные и неравномерные коды
Различают равномерные и неравномерные коды. Равномерные коды в кодовых комбинациях содержат одинаковое число символов, неравномерные — разное.
Выше мы рассмотрели равномерные двоичные коды.
Примером неравномерного кода может служить азбука Морзе, в которой для каждой буквы и цифры определена последовательность коротких и длинных сигналов. Так, букве Б соответствует короткий сигнал («точка»), а букве Ш — четыре длинных сигнала (четыре «тире»). Неравномерное кодирование позволяет повысить скорость передачи сообщений за счёт того, что наиболее часто встречающиеся в передаваемой информации символы имеют самые короткие кодовые комбинации.
Следующая страница 
Информатика. 7 класс
Конспект урока
Кодирование информации. Двоичный код
Перечень вопросов, рассматриваемых в теме:
Дискретизация информации – процесс преобразования информации из непрерывной формы представления в дискретную. Чтобы представить информацию в дискретной форме, её следует выразить с помощью символов какого-нибудь естественного или формального языка.
Алфавит языка – конечный набор отличных друг от друга символов, используемых для представления информации. Мощность алфавита – это количество входящих в него символов.
Алфавит, содержащий два символа, называется двоичным алфавитом. Представление информации с помощью двоичного алфавита называют двоичным кодированием. Двоичное кодирование универсально, так как с его помощью может быть представлена любая информация.
1. Босова Л. Л. Информатика: 7 класс. // Босова Л. Л., Босова А. Ю. – М.: БИНОМ, 2017. – 226 с.
Теоретический материал для самостоятельного изучения
Для решения своих задач человеку часто приходится преобразовывать имеющуюся информацию из одной формы представления в другую. Например, при чтении вслух происходит преобразование информации из дискретной (текстовой) формы в непрерывную (звук). Во время диктанта на уроке русского языка, наоборот, происходит преобразование информации из непрерывной формы (голос учителя) в дискретную (записи учеников).
Информация, представленная в дискретной форме, значительно проще для передачи, хранения или автоматической обработки. Поэтому в компьютерной технике большое внимание уделяется методам преобразования информации из непрерывной формы в дискретную.
Дискретизация информации – процесс преобразования информации из непрерывной формы представления в дискретную.
Рассмотрим суть процесса дискретизации информации на примере.
На метеорологических станциях имеются самопишущие приборы для непрерывной записи атмосферного давления. Результатом их работы являются барограммы – кривые, показывающие, как изменялось давление в течение длительных промежутков времени. Одна из таких кривых, вычерченная прибором в течение семи часов проведения наблюдений, показана на рисунке 1.
На основании полученной информации можно построить таблицу, содержащую показания прибора в начале измерений и на конец каждого часа наблюдений.
Полученная таблица даёт не совсем полную картину того, как изменялось давление за время наблюдений: например, не указано самое большое значение давления, имевшее место в течение четвёртого часа наблюдений. Но если занести в таблицу значения давления, наблюдаемые каждые полчаса или 15 минут, то новая таблица будет давать более полное представление о том, как изменялось давление.
Таким образом, информацию, представленную в непрерывной форме (барограмму, кривую), мы с некоторой потерей точности преобразовали в дискретную форму (таблицу).
В дальнейшем вы познакомитесь со способами дискретного представления звуковой и графической информации.
В общем случае, чтобы представить информацию в дискретной форме, её следует выразить с помощью символов какого-нибудь естественного или формального языка. Таких языков тысячи. Каждый язык имеет свой алфавит.
Алфавит – конечный набор отличных друг от друга символов (знаков), используемых для представления информации. Мощность алфавита – это количество входящих в него символов (знаков).
Алфавит, содержащий два символа, называется двоичным алфавитом (рис. 3). Представление информации с помощью двоичного алфавита называют двоичным кодированием. Закодировав таким способом информацию, мы получим её двоичный код.
Рассмотрим в качестве символов двоичного алфавита цифры 0 и 1. Покажем, что любой алфавит можно заменить двоичным алфавитом. Прежде всего, присвоим каждому символу рассматриваемого алфавита порядковый номер. Номер представим с помощью двоичного алфавита. Полученный двоичный код будем считать кодом исходного символа.
Если мощность исходного алфавита больше двух, то для кодирования символа этого алфавита потребуется не один, а несколько двоичных символов. Другими словами, порядковому номеру каждого символа исходного алфавита будет поставлена в соответствие цепочка (последовательность) из нескольких двоичных символов. Правило получения двоичных кодов для символов алфавита мощностью больше двух можно представить схемой на рисунке.
Двоичные символы (0,1) здесь берутся в заданном алфавитном порядке и размещаются слева направо. Двоичные коды (цепочки символов) читаются сверху вниз. Все цепочки (кодовые комбинации) из двух двоичных символов позволяют представить четыре различных символа произвольного алфавита:
Цепочки из трёх двоичных символов получаются дополнением двухразрядных двоичных кодов справа символом 0 или 1. В итоге кодовых комбинаций из трёх двоичных символов получается 8 – вдвое больше, чем из двух двоичных символов:
Соответственно, четырёхразрядный двоичный код позволяет получить 16 кодовых комбинаций, пятиразрядный – 32, шестиразрядный – 64 и т. д.
Длину двоичной цепочки – количество символов в двоичном коде – называют разрядностью двоичного кода.
Обратите внимание, что:
32 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 и т. д.
Здесь количество кодовых комбинаций представляет собой произведение некоторого количества одинаковых множителей, равного разрядности двоичного кода.
Если количество кодовых комбинаций обозначить буквой N, а разрядность двоичного кода – буквой i, то выявленная закономерность в общем виде будет записана так:
В математике такие произведения записывают в виде:
Запись 2 i читают так: «2 в i-й степени».
Задача. Вождь племени Мульти поручил своему министру разработать двоичный код и перевести в него всю важную информацию. Двоичный код какой разрядности потребуется, если алфавит, используемый племенем Мульти, содержит 16 символов? Выпишите все кодовые комбинации.
Чтобы выписать все кодовые комбинации из четырёх 0 и 1, воспользуемся схемой на рис. 1.13: 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111.
Универсальность двоичного кодирования
В начале нашей беседы вы узнали, что информация, представленная в непрерывной форме, может быть выражена с помощью символов некоторого естественного или формального языка. В свою очередь, символы произвольного алфавита могут быть преобразованы в двоичный код. Таким образом, с помощью двоичного кода может быть представлена любая информация на естественных и формальных языках, а также изображения и звуки (рис. 6). Это и означает универсальность двоичного кодирования.
Двоичные коды широко используются в компьютерной технике, требуя только двух состояний электронной схемы – «включено» (это соответствует цифре 1) и «выключено» (это соответствует цифре 0).
Простота технической реализации – главное достоинство двоичного кодирования. Недостаток двоичного кодирования – большая длина получаемого кода.
Равномерные и неравномерные коды
Различают равномерные и неравномерные коды. Равномерные коды в кодовых комбинациях содержат одинаковое число символов, неравномерные – разное.
Выше мы рассмотрели равномерные двоичные коды.
Примером неравномерного кода может служить азбука Морзе, в которой для каждой буквы и цифры определена последовательность коротких и длинных сигналов. Так, букве Е соответствует короткий сигнал («точка»), а букве Ш – четыре длинных сигнала (четыре «тире»). Неравномерное кодирование позволяет повысить скорость передачи сообщений за счёт того, что наиболее часто встречающиеся в передаваемой информации символы имеют самые короткие кодовые комбинации.
Разбор решения заданий тренировочного модуля
№1.Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Переведите десятичное число 273 в двоичную систему счисления.
Воспользуемся алгоритмом перевода целых чисел из системы с основанием p в систему с основанием q:
1. Основание новой системы счисления выразить цифрами исходной системы счисления и все последующие действия производить в исходной системе счисления.
2. Последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получим частное, меньшее делителя.
3. Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
4. Составить число в новой системе счисления, записывая его, начиная с последнего остатка.
Ответ: 27310= 100010001.
№2. Тип задания: единичный / множественный выбор.
Четыре буквы латинского алфавита закодированы кодами различной длины: