Прямоугольник с равными сторонами это что
Что такое прямоугольник: определение, свойства, признаки, формулы
В данной публикации мы рассмотрим определение, свойства и признаки одной из основных геометрических фигур – прямоугольника. Также приведем формулы, с помощью которых можно найти его площадь и периметр.
Определение прямоугольника
Прямоугольник – это четырехугольник, у которого все углы равны 90° (т.е. являются прямыми).
∠ABC = ∠BCD = ∠BAD = ADC = 90°
Прямоугольник состоит из:
Сам прямоугольник обычно записывается путем перечисления его вершин, например, ABCD в нашем случае.
Примечание: Прямоугольник является разновидностью параллелограмма.
Свойства прямоугольника
Свойство 1
Противоположные стороны прямоугольника попарно параллельны и равны.
Свойство 2
Длина и ширина прямоугольника одновременно являются его высотами, т.к. они взаимно перпендикулярны.
Свойство 3
Если соединить середины сторон прямоугольника, то получится ромб.
Свойство 4
Квадрат диагонали (d) прямоугольника равняется сумме квадратов его смежных сторон.
d 2 = a 2 + b 2
Это следует из теоремы Пифагора, которую можно применить к любому из прямоугольных треугольников, которые образуются в результате деления диагональю прямоугольника.
Свойство 5
Диагонали прямоугольника равны, и в точке пересечения делятся пополам.
Свойство 6
Около любого прямоугольника можно описать окружность, радиус (R) которой равен половине диагонали этого прямоугольника.
Следовательно, диаметр окружности равен полной длине диагонали прямоугольника.
Признаки прямоугольника
Параллелограмм является прямоугольником, если верно одно из следующих утверждений:
Формулы
1. Площадь прямоугольника (S):
2. Периметр прямоугольника (P):
Признаки равенства прямоугольников
Признаки равенства прямоугольников — это признаки, c
помощью которых можно доказать, что прямоугольники равны.
В этой статье мы рассмотрим и докажем четыре признака
равенства прямоугольников. С помощью этих признаков
можно доказать, равенство двух и более геометрических
фигур — в данном случае прямоугольников.
I признак равенства прямоугольников
Формулировка первого признака равенства
прямоугольников:
Если две неравных стороны одного прямоугольника
соответственно равны двум неравным сторонам другого
прямоугольника, то такие прямоугольники равны.
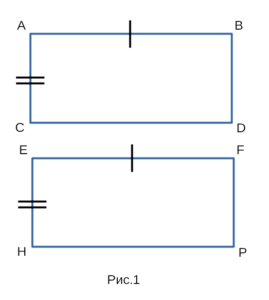
Докажем, что прямоугольники ABDC и EFPH,
изображенные на рисунке 1 равны между собой.
Доказательство первого признака равенства
прямоугольников:
II признак равенства прямоугольников
По сумме квадратов двух неравных сторон.
Формулировка второго признака равенства
прямоугольников:
Если сумма квадратов двух неравных сторон одного прямоугольника
соответственно равна сумме квадратов двух неравных сторон
другого прямоугольника, то они равны.
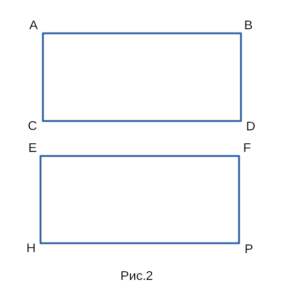
Докажем, что прямоугольники ABDC и EFPH, изображенные
на рисунке 2 равны между собой.
Доказательство второго признака равенства
прямоугольников:
III признак равенства прямоугольников
По диаметру описанной окружности.
Формулировка третьего признака равенства
прямоугольников:
Если диаметр описанной окружности одного прямоугольника
соответственно равен диаметру описанной окружности другого
прямоугольника, то такие прямоугольники равны.
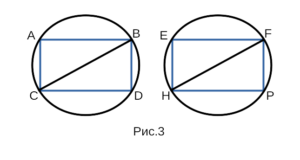
Докажем, что прямоугольники ABDC и EFPH, изображенные
на рисунке 3 равны между собой.
Доказательство третьего признака равенства
прямоугольников:
IV признак равенства прямоугольников
По равным и параллельным противоположным сторонам.
Формулировка четвертого признака равенства
прямоугольников:
Если противоположные стороны одного прямоугольника соответственно
параллельны и равны противоположным сторонам другого прямоугольника,
то такие прямоугольники равны.
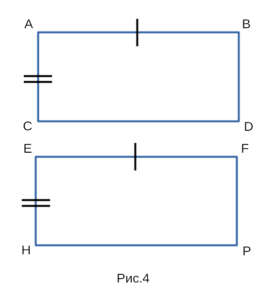
Докажем, что прямоугольники ABDC и EFPH, изображенные
на рисунке 4 равны между собой.
Доказательство четвертого признака равенства
прямоугольников:
В этой статье мы доказали равенство прямоугольников по всем четырем признакам.
Прямоугольник, свойства, признаки и формулы
Прямоугольник, свойства, признаки и формулы.
Прямоугольник – это четырехугольник, у которого все углы прямые (каждый из углов равен 90 градусам).
Прямоугольник (понятие, определение):
Прямоугольник – это четырехугольник, у которого все углы прямые (каждый из углов равен 90 градусам).
Прямоугольник – это четырехугольник, у которого каждый угол является прямым.
Прямоугольник – это четырехугольник, у которого две противоположные стороны равны между собой и все четыре угла равны между собой и каждый из них составляет 90 градусов.
Рис. 1. Прямоугольник
В свою очередь четырёхугольник (греч. τετραγωνον) – это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), последовательно соединяющих эти точки.
Длинную сторону прямоугольника называют длиной прямоугольника, а короткую – шириной прямоугольника.
Свойства прямоугольника:
1. Прямоугольник является параллелограммом – его противоположные стороны попарно параллельны.
Рис. 2. Прямоугольник
2. Противоположные стороны прямоугольника равны.
Рис. 3. Прямоугольник
3. Стороны прямоугольника являются его высотами.
4. Прилегающие стороны прямоугольника всегда перпендикулярны.
Рис. 4. Прямоугольник
5. Каждый угол прямоугольника прямой и равен 90 градусам. Сумма всех углов прямоугольника составляет 360 градусов.
Рис. 5. Прямоугольник
6. Диагонали прямоугольника равны.
Рис. 6. Прямоугольник
Рис. 7. Прямоугольник
8. Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон (что вытекает из теоремы Пифагора).
Рис. 8. Прямоугольник
9. Диагонали прямоугольника делятся точкой пересечения пополам.
10. Около любого прямоугольника можно описать окружность. Диагональ прямоугольника является диаметром описанной окружности.
АС и BD – диаметр описанной окружности и диагональ прямоугольника
11. Точка пересечения диагоналей называется центром прямоугольника и является центром описанной окружности.
12. Прямоугольник может содержать вписанную окружность и только одну, если все его стороны равны, т.е. он является квадратом.
Признаки прямоугольника:
– если диагонали параллелограмма равны, то он является прямоугольником;
– если квадрат диагонали параллелограмма равен сумме квадратов смежных сторон, то он (параллелограмм) является прямоугольником;
– если углы параллелограмма равны, то он является прямоугольником.
Формулы прямоугольника:
Пусть a – длина прямоугольника, b – ширина прямоугольника, d – диагональ и диаметр описанной окружности прямоугольника, R – радиус описанной окружности прямоугольника, P – периметр прямоугольника, S – площадь прямоугольника.
Формула стороны прямоугольника (длины и ширины прямоугольника):




Формула диагонали прямоугольника:

Формулы периметра прямоугольника:
Формулы площади прямоугольника:
Формула радиуса окружности, описанной вокруг прямоугольника:

Примечание: © Фото https://www.pexels.com, https://pixabay.com
Мировая экономика
Справочники
Востребованные технологии
Поиск технологий
О чём данный сайт?
Настоящий сайт посвящен авторским научным разработкам в области экономики и научной идее осуществления Второй индустриализации России.
Он включает в себя:
– экономику Второй индустриализации России,
– теорию, методологию и инструментарий инновационного развития – осуществления Второй индустриализации России,
– организационный механизм осуществления Второй индустриализации России,
– справочник прорывных технологий.
Мы не продаем товары, технологии и пр. производителей и изобретателей! Необходимо обращаться к ним напрямую!
Мы проводим переговоры с производителями и изобретателями отечественных прорывных технологий и даем рекомендации по их использованию.
О Второй индустриализации
Осуществление Второй индустриализации России базируется на качественно новой научной основе (теории, методологии и инструментарии), разработанной авторами сайта.
Конечным результатом Второй индустриализации России является повышение благосостояния каждого члена общества: рядового человека, предприятия и государства.
Вторая индустриализация России есть совокупность научно-технических и иных инновационных идей, проектов и разработок, имеющих возможность быть широко реализованными в практике хозяйственной деятельности в короткие сроки (3-5 лет), которые обеспечат качественно новое прогрессивное развитие общества в предстоящие 50-75 лет.
Та из стран, которая первой осуществит этот комплексный прорыв – Россия, станет лидером в мировом сообществе и останется недосягаемой для других стран на века.
Прямоугольник
Прямоугольник — параллелограмм, у которого все углы прямые.
Частным случаем прямоугольника является квадрат.
Свойства прямоугольника
1. Так как прямоугольник – это параллелограмм, то все свойства параллелограмма верны и для прямоугольника.
Помимо этого:
2. Стороны прямоугольника являются его высотами.
3. Диагонали прямоугольника равны.
4. Квадрат диагонали прямоугольника равен сумме квадратов двух его соседних сторон.
5. Около любого прямоугольника можно описать окружность, при этом диагональ прямоугольника равна диаметру описанной окружности.
Признаки параллелограмма
Параллелограмм является прямоугольником, если выполняется любое из условий:
1. Диагонали параллелограмма равны.
2. Квадрат диагонали параллелограмма равен сумме квадратов соседних сторон.
3. Все углы параллелограмма равны.
Площадь прямоугольника
Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Прямоугольник с равными сторонами называется?
Прямоугольник,у которого все стороны равны это?
В математике этот прямоугольник называется квадратом, но это одновременно ромб и параллелограмм.
А вообще прямоугольник с равными сторонами частенько видим в обычной жизни
Боксерский ринг и каре (квадрат из пехотинцев) тоже подходят нашим требованиям.
Прямоугольник, все стороны которого равны между собой, называется квадратом. А прямоугольником, в свою очередь, называют параллелепипед все углы которого равны 90 градусам. А параллелепипедом называют четырехугольник, противоположные стороны которой являются параллельными.
прямоугольник, у которого все стороны равны между собой, называется квадратом. чтобы найти площадь такого прямоугольника, нужно длину его стороны возвести в квадрат. чтобы найти периметр, нужно длину его стороны умножить на 4.
На этот вопрос ответит любой школьник. Прямоугольник, все стороны которого равны, называется не иначе как «квадрат». Также можно отметить, что кроме сторон у квадрата и все углы равны (90 градусов). Поэтому квадрат называют правильным четырехугольником. Кроме того у квадрата равны и диагонали. При этом они взаимно перпендикулярны.
Со школы все помнят, что у квадрата все стороны равны. Кроме того, он является правильным четырехугольником, у которого все углы равны и составляют девяносто градусов. Квадрат является разновидностью прямоугольника, параллелограмма и ромба. У квадрата могут быть две диагонали.