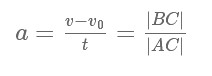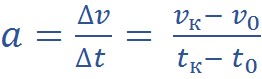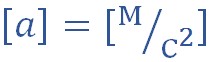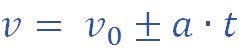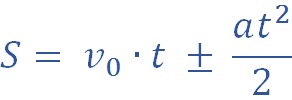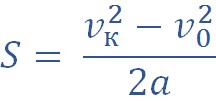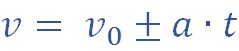Прямолинейное равноускоренное движение что это

Равноускоренное движение: формулы и примеры

Содержание:

Определение

Равноускоренным движением в физике считается такое движение, вектор ускорения которого не меняется по модулю и направлению. Говоря простым языком, равноускоренное движение представляет собой неравномерное движение (то есть идущее с разной скоростью), ускорение которого является постоянным на протяжении определенного промежутка времени. Представим себе автомобиль, который начинает двигаться, первые 2 секунды его скорость равна 10 м/с, следующие 2 секунды он уже движется со скоростью 20 м/с, а еще через 2 секунды уже со скоростью 30 м/с. То есть каждые 2 секунды он ускоряется на 10 м/с, такое движение и есть равноускоренным.

Отсюда можно вывести предельно простое определение равноускоренного движения: это такое движение любого физического тела, при котором его скорость за равные промежутки времени изменяется одинаково.

Примеры

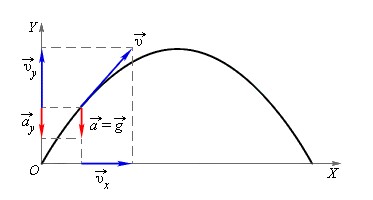
Наглядным примером равноускоренного движения в повседневной жизни может быть велосипед, едущий с горки вниз (но не велосипед, управляемый велосипедистом), или брошенный камень под определенным углом к горизонту.

К слову пример с камнем можно рассмотреть более детально. В любой точке траектории полета на камень действует ускорение свободного падения g. Ускорение g не меняется, то есть остается константой и всегда направлено в одну сторону (по сути, это главное условие равноускоренного движения).

Полет брошенного камня удобно представить в виде сумы движений относительно вертикальной и горизонтальной оси системы координат.

Если вдоль оси Х движение камня будет равномерным и прямолинейным, то вдоль оси Y равноускоренным и прямолинейным.

Формула

Формула скорости при равноускоренном движении будет иметь такой вид:

Где V₀ – это начальная скорость тела, а – ускорение (как мы помним, эта величина является константой), t – общее время полета камня.

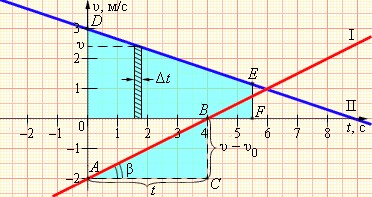
При равноускоренном движении зависимость V(t) будет иметь вид прямой линии.

Ускорение может быть определено по углу наклона графика скорости. На этом рисунке оно равно отношению сторон треугольника АВС.

Чем больше угол β, тем больше наклон и как следствие, крутизна графика по отношению к оси времени, и тем больше будет ускорение тела.

Рекомендуемая литература по теме

Видео

Автор: Павел Чайка, главный редактор журнала Познавайка

При написании статьи старался сделать ее максимально интересной, полезной и качественной. Буду благодарен за любую обратную связь и конструктивную критику в виде комментариев к статье. Также Ваше пожелание/вопрос/предложение можете написать на мою почту pavelchaika1983@gmail.com или в Фейсбук, с уважением автор.

Похожие посты:

Один комментарий

Источник

Равноускоренное движение.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: виды механического движения, скорость, ускорение, уравнения прямолинейного равноускоренного движения, свободное падение.

Зависимость скорости от времени.

При изучении равномерного прямолинейного движения вопрос зависимости скорости от времени не возникал: скорость была постоянна в процессе движения. Однако при равноускоренном движении скорость меняется с течением времени, и эту зависимость нам предстоит выяснить.

Давайте ещё раз потренируемся в элементарном интегрировании. Исходим из того, что производная вектора скорости есть вектор ускорения:

В конкретных задачах мы выбираем систему координат и переходим к проекциям на координатные оси. Часто хватает двух осей и прямоугольной декартовой системы координат, и векторная формула (3) даёт два скалярных равенства:

Формула для третьей компоненты скорости, если она необходима, выглядит аналогично.)

Закон движения.

Теперь мы можем найти закон движения, то есть зависимость радиус-вектора от времени. Вспоминаем, что производная радиус-вектора есть скорость тела:

Подставляем сюда выражение для скорости, даваемое формулой (3) :

Переходя к проекциям на координатные оси, вместо одного векторного равенства (7) получаем три скалярных равенства:

Прямолинейное равноускоренное движение.

Но очень часто помогает ещё одна формула, являющаяся их следствием. Выразим из первой формулы время:

и подставим в формулу для перемещения:

После алгебраических преобразований (проделайте их обязательно!) придём к соотношению:

Эта формула не содержит времени и позволяет быстрее приходить к ответу в тех задачах, где время не фигурирует.

Свободное падение.

Важным частным случаем равноускоренного движения является свободное падение. Так называется движение тела вблизи поверхности Земли без учёта сопротивления воздуха.

Давайте разберём несколько задач и посмотрим, как работают выведенные нами формулы для равноускоренного движения.

Задача. Найти скорость приземления дождевой капли, если высота тучи км.

Решение. Направим ось вертикально вниз, расположив начало отсчёта в точке отрыва капли. Воспользуемся формулой

На самом деле капли дождя падают со скоростью порядка нескольких метров в секунду. Почему такое расхождение? Сопротивление воздуха!

Задача. Тело брошено вертикально вверх со скоростью м/с. Найти его скорость через c.

Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу

Задача. С балкона, находящегося на высоте м, бросили вертикально вверх камень со скоростью м/с. Через какое время камень упадёт на землю?

Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу

Горизонтальный бросок.

Равноускоренное движение не обязательно является прямолинейным. Рассмотрим движение тела, брошенного горизонтально.

Рис. 1. Горизонтальный бросок

Время полёта найдём из условия, что в момент падения координата тела обращается в нуль:

Бросок под углом к горизонту.

Рассмотрим несколько более сложный случай равноускоренного движения: полёт тела, брошенного под углом к горизонту.

Рис. 2. Бросок под углом к горизонту

Начинаем с уравнений:

Дальше действуем так же, как и в случае горизонтального броска. В результате приходим к соотношениям:

(Обязательно проделайте эти вычисления самостоятельно!) Как видим, зависимость от снова является уравнением параболы.Попробуйте также показать, что максимальная высота подъёма определяется формулой:

Источник

Учебники

Журнал «Квант»

Общие

Т. Равноускоренное движение

Равноускоренное прямолинейное движение

Равноускоренное прямолинейное движение — это движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково, т. е. это движение с постоянным по модулю и направлению ускорением.

\vec a = \operatorname\) — уравнение ускорения.

По определению ускорения \(

Пусть в момент времени t₀ = 0 скорость тела равна \(

\vec \upsilon_0\), в момент времени t — \(

\vec \upsilon\). Тогда за промежуток времени \(

\vec \upsilon = \vec \upsilon_0 + \vec a \cdot t\) — уравнение скорости.

\upsilon_x = \upsilon_ <0x>+ a_x \cdot t\].

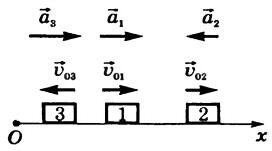
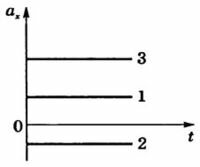
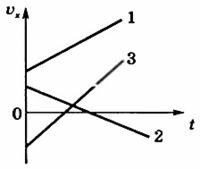
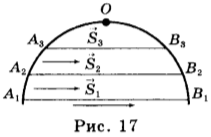
Эти зависимости кинематических величин от времени изобразим графически для трех тел (рис. 1).

Графики ускорения a_x = f(t) представлены на рисунке 2, а графики скорости υ_x = f(t) — на рисунке 3.

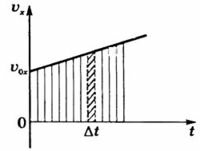
Для нахождения перемещения воспользуемся графиком скорости (рис. 4).

Для малого промежутка времени Δt изменением величины скорости можно пренебречь и скорость можно считать постоянной. Тогда перемещение за промежуток времени Δt будет равно площади узкой густо заштрихованной полоски. Мысленно разбив все время движения тела на малые промежутки времени и найдя перемещение за каждый отдельный промежуток времени, суммируем эти перемещения. Модуль проекции перемещения за промежуток времени \(

\upsilon_x = \upsilon_ <0x>+ a_x \cdot t\) в (1), получим:

\Delta r_x = \upsilon_ <0x>\cdot t + \frac<2>\) — уравнение перемещения в проекциях;

\Delta \vec r = \vec \upsilon_0 \cdot t + \frac<\vec a \cdot t^2><2>\) — уравнение перемещения в векторном виде.

x = x_0 + \Delta r_x\), имеем:

x = x_0 + \upsilon_ <0x>\cdot t + \frac<2>\) — кинематическое уравнение равноускоренного движения.

Исключая из уравнений скорости и перемещения время t, получим:

Сравнивая выражение (1) с формулой \(

\Delta r_x = \left\langle \upsilon \right\rangle_x \cdot t\), найдем:

\left\langle \upsilon \right\rangle_x = \frac <\upsilon_<0x>+ \upsilon_x><2>\) — проекция средней скорости при равноускоренном движении.

Графиком перемещения является парабола, положение вершины которой зависит от направлений начальной скорости и ускорения (рис. 5).

Источник

Равноускоренное движение

Ускорение – физическая величина, показывающая быстроту изменения скорости. Ускорение равно отношению изменения скорости за промежуток времени к величине этого промежутка

Если ускорение и скорость тела направлены в одну сторону, то модуль скорости тела увеличивается, оно разгоняется.

Если ускорение и скорость тела направлены в разные стороны, то модуль скорости тела уменьшается, тело тормозит.

Ускорение в системе СИ измеряется в м/с 2 (метрах, деленных на секунду в квадрате).

Так как ускорение при данном виде движения остается неизменным, то скорость является линейной функцией и вычисляется по формуле:

Перемещение можно рассчитать, применяя следующие формулы:

Обратим внимание, что вторую формулу удобно использовать в задачах, где не дано время движения.

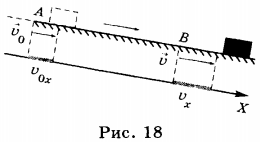
Для прямолинейного равноускоренного движения закон движения выглядит следующим образом:

В записанных уравнениях постановка знаков ± связана со знаками проекций величин скорости, ускорения и перемещения.

Рассмотрим основные графики величин для равноускоренного прямолинейного движения.

Так как модуль ускорения при равноускоренном движении со временем не изменяется, то его график будет представлен в виде прямой линии, параллельной оси времени.

Рис.2.
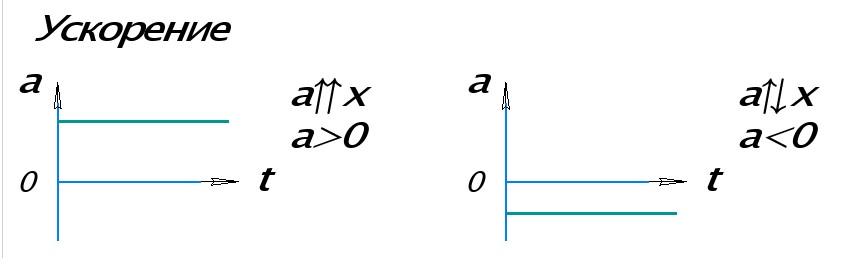
Графики ускорения при равноускоренном прямолинейном движении

На левом рисунке проекция ускорения на ось ОХ, вдоль которой движется тело, положительная. Поэтому график ускорения лежит выше горизонтальной оси t. На правом рисунке ускорение направлено против оси ОХ, его проекция отрицательная. График лежит ниже оси t.

Так как величина скорости тела при данном виде движения рассчитывается по формуле

то ее график будет выглядеть как линейная функция (прямая, расположенная под углом к оси t, исходящая из точки начальной скорости).

На графике слева проекция скорости положительная (υ>0), проекция ускорения тоже положительная (a>0), т.к. скорость тела возрастает со временем. График лежит выше оси t.

На графике справа тело перемещается в направлении, обратном направлению оси ОХ, поэтому проекция скорости отрицательна. Проекция ускорения тоже отрицательна (a 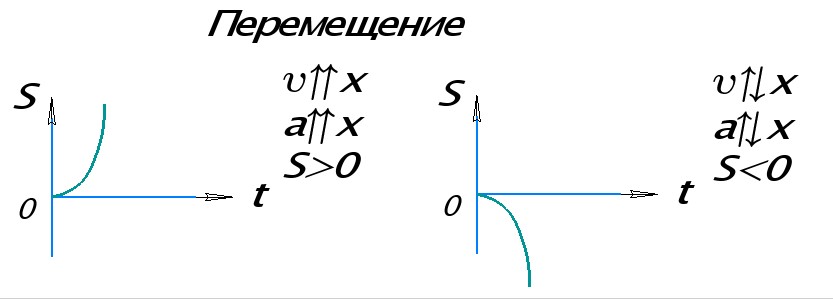Рис.4. Графики перемещения при равноускоренном прямолинейном движении

Если ветвь параболы направлена вверх на графике, значит ускорение на этом участке сонаправлено с осью ОХ. Если ветвь параболы направлена вниз, то ускорение направлено против оси ОХ.

График координаты тела представляет собой график перемещения с учетом начальной координаты x₀.

Остальные тонкости анализа графиков прямолинейного движения будут рассмотрены в отдельной главе.

Источник

Скорость. Ускорение. Равноускоренное прямолинейное движение

1. Реальное механическое движение — это движение с изменяющейся скоростью. Движение, скорость которого стечением времени изменяется, называют неравномерным движением.

При неравномерном движении координату тола уже нельзя определить но формуле ​ \( x=x_0+v_xt \) ​, так как значение скорости движения не является постоянным. Поэтому для характеристики быстроты изменения положения тела с течением времени при неравномерном движении вводят величину, называемую средней скоростью.

Средней скоростью ​ \( \vec_ <ср>\) ​ неравномерного движения называют физическую величину, равную отношению перемещении \( \vec \) тела ко времени ​ \( t \) ​, за которое оно произошло: ​ \( \vec_<ср>=\frac\) ​.

2. Важно, что, зная среднюю скорость неравномерного движения на каком-либо участке траектории, нельзя определить положение тела на этой траектории в любой момент времени. Например, если средняя скорость движения автомобиля за 2 часа 50 км/ч, то мы не можем сказать, где он находился через 0,5 часа от начала движения, через 1 час, 1,5 часа и т.п., поскольку он мог первые полчаса двигаться со скоростью 80 км/ч, затем какое-то время стоять, а какое-то время ехать в пробке со скоростью 20 км/ч.

3. Двигаясь по траектории, тело проходит последовательно все её точки. В каждой точке траектории оно находится в определённые моменты времени и имеет какую-то скорость.

Мгновенной скоростью называют скорость тела в данный момент времени в данной точке траектории.

При дальнейшем уменьшении перемещения и соответственно времени движения тела они станут такими маленькими, что прибор, например спидометр, перестанет фиксировать изменение скорости, и движение за этот малый промежуток времени можно считать равномерным. Средняя скорость на этом участке и есть мгновенная скорость тела в т.О.

4. Одним из видов неравномерного движения является равноускоренное движение. Равноускоренным движением называют движение, при котором скорость тела за любые равные промежутки времени изменяется на одно и то же значение.

Слова «любые равные промежутки времени» означают, что какие бы равные промежутки времени (2 с, 1 с, доли секунды и т.п.) мы ни взяли, скорость всегда будет изменяться одинаково. При этом её модуль может как увеличиваться, так и уменьшаться.

5. Характеристикой равноускоренного движения, помимо скорости и перемещения, является ускорение.

Ускорение тела при равноускоренном движении — векторная физическая величина, равная отношению изменения скорости тела к промежутку времени, за который это изменение произошло.

Направление ускорения совпадает с направлением скорости движения, если модуль скорости увеличивается, ускорение направлено противоположно скорости движения, если модуль скорости уменьшается.

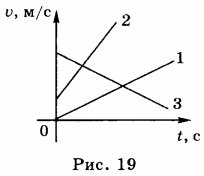
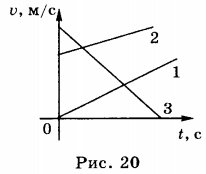
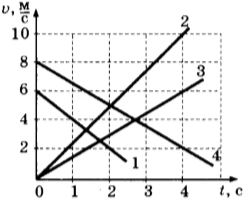
7. Как видно из формулы скорости равноускоренного движения, она линейно зависит от времени. Графиком зависимости модуля скорости от времени является прямая, составляющая некоторый угол с осью абсцисс (осью времени). На рисунке 19 приведены графики зависимости модуля скорости от времени.

График 1 соответствует движению без начальной скорости с ускорением, направленным так же, как и скорость; график 2 — движению с начальной скоростью \( v_ <02>\) и с ускорением, направленным так же, как и скорость; график 3 — движению с начальной скоростью \( v_ <03>\) и с ускорением, направленным в сторону, противоположную направлению скорости.

8. На рисунке приведены графики зависимости проекции скорости равноускоренного движения от времени (рис. 20).

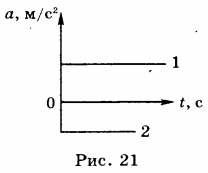
9. На рисунке 21 приведены графики зависимости проекции ускорения равноускоренного движения от времени.

График 1 соответствует движению, проекция ускорения которого положительна, график 2 — движению, проекция ускорения которого отрицательна.

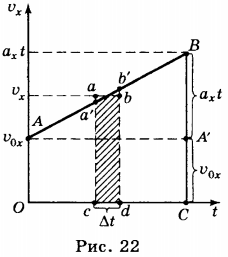
10. Формулу перемещения тела при равноускоренном движении можно получить, используя график зависимости проекции скорости этого движения от времени (рис. 22).

Выделим на графике малый участок ​ \( ab \) ​ и опустим перпендикуляры из точек​ \( a \) ​ и ​ \( b \) ​ на ось абсцисс. Если промежуток времени ​ \( \Delta\) ​, соответствующий участку ​ \( cd \) ​ на оси абсцисс мал, то можно считать, что скорость в течение этого промежутка времени не изменяется и тело движется равномерно. В этом случае фигура ​ \( cabd \) ​ мало отличается от прямоугольника и её площадь численно равна проекции перемещения тела за время, соответствующее отрезку ​ \( cd \) ​.

На такие полоски можно разбить всю фигуру ОАВС, и её площадь равна сумме площадей всех полосок. Следовательно, проекция перемещения тела за время ​ \( t \) ​ численно равна площади трапеции ОАВС. Площадь трапеции равна произведению полусуммы её оснований на высоту: ​ \( S_x= \frac<1><2>(OA+BC)OC \) ​.

Полученная формула позволяет определить положение (координату) тела в любой момент времени, если известны начальная скорость, начальная координата и ускорение.

Если начальная скорость тела равна нулю, то: ​ \( v^2_x=2a_xs_x \) ​.

Полученная формула позволяет рассчитать тормозной путь транспортных средств, т.е. путь, который проезжает, например, автомобиль до полной остановки. При некотором ускорении движения, которое зависит от массы автомобиля и силы тяги двигателя, тормозной путь тем больше, чем больше начальная скорость автомобиля.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

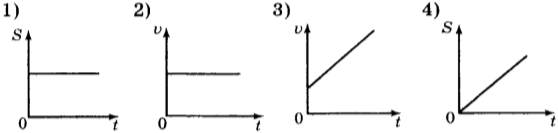
1. Hа рисунке приведены графики зависимости пути и скорости тела от времени. Какой график соответствует равноускоренному движению?

2. Автомобиль, начав двигаться из состояния покоя но прямолинейной дороге, за 10 с приобрел скорость 20 м/с. Чему равно ускорение автомобиля?

1) 200 м/с 2
2) 20 м/с 2
3) 2 м/с 2
4) 0,5 м/с 2

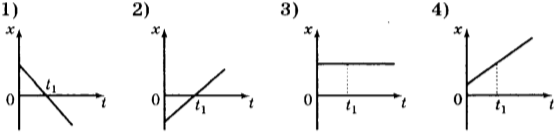
3. На рисунках представлены графики зависимости координаты от времени для четырёх тел, движущихся вдоль оси ​ \( Оx \) ​. У какого из тел в момент времени ​ \( t_1 \) ​ скорость движения равна нулю?

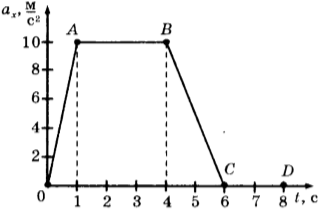
4. На рисунке представлен график зависимости проекции ускорения от времени для тела, движущегося прямолинейно вдоль оси ​ \( Оx \) ​.

Равноускоренному движению соответствует участок

1) только ОА
2) только АВ
3) только ОА и ВС
4) только CD

5. При изучении равноускоренного движения измеряли путь, пройденный телом из состояния покоя за последовательные равные промежутки времени (за первую секунду, за вторую секунду и т.д.). Полученные данные приведены в таблице.

Чему равен путь, пройденный телом за третью секунду?

1) 4 м
2) 4,5 м
3) 5 м
4) 9 м

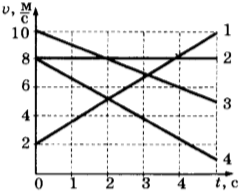
6. На рисунке представлены графики зависимости скорости движения от времени для четырёх тел. Тела движутся по прямой.

Для какого(-их) из тел — 1, 2, 3 или 4 — вектор ускорения направлен противоположно вектору скорости?

1) только 1
2) только 2
3) только 4
4) 3 и 4

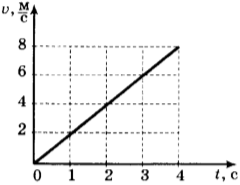
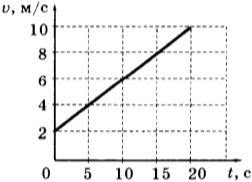
7. Используя график зависимости скорости движения тела от времени, определите его ускорение.

8. При изучении равноускоренного движения измеряли скорость тела в определённые моменты времени. Полученные данные, приведены в таблице. Чему равна скорость тела в момент времени 3 с?

1) 0 м/с
2) 2 м/с
3) 4 м/с
4) 14 м/с

10. Используя график зависимости скорости движения тела от времени, определите скорость тела в конце 30-й секунды. Считать, что характер движения тела не изменился.

1) 14 м/с
2) 20 м/с
3) 62 м/с
4) 69,5 м/с

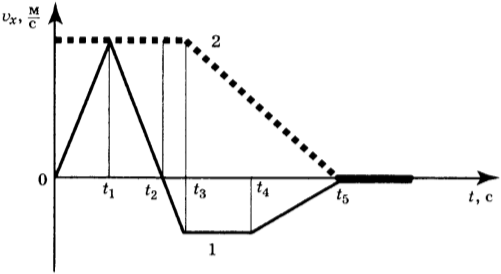
11. Два тела движутся по оси ​ \( Оx \) ​. На рисунке представлены графики зависимости проекции скорости движения тел 1 и 2 от времени.

Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) В промежутке времени ​ \( t_3-t_5 \) ​ тело 2 движется равноускоренно.
2) К моменту времени ​ \( t_2 \) ​ от начала движения тела прошли одинаковые пути.
3) В промежутке времени ​ \( 0-t_3 \) ​ тело 2 находится в покое.
4) В момент времени ​ \( t_5 \) ​ тело 1 останавливается.
5) В промежутке времени ​ \( t_3-t_4 \) ​ ускорение ​ \( a_x \) ​ тела 1 отрицательно.

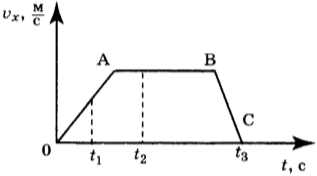
12. На рисунке представлен график зависимости проекции скорости от времени для тела, движущегося вдоль оси Ох.

Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) Участок ОА соответствует ускоренному движению тела.
2) Участок АВ соответствует состоянию покоя тела.
3) В момент времени ​ \( t_1 \) ​ тело имело максимальное по модулю ускорение.
4) Момент времени ​ \( t_3 \) ​ соответствует остановке тела.
5) В момент времени ​ \( t_2 \) ​ тело имело максимальное по модулю ускорение.

Часть 2

13. Зависимость координаты от времени для некоторого тела описывается уравнением ​ \( x=12t-t^2 \) ​. В какой момент времени скорость движения равна нулю?

Источник