Простые числа что это такое 6 класс
Простые числа – это натуральные числа, их можно разделить только на два значения: единицу и себя. К натуральным относят те, которые используются во время счета, поэтому должно выполняться требование, чтобы они были положительными и целыми. Делители также не должны быть отрицательными и дробными.
Они широко применяются в криптографии, когда необходимо закодировать важную информацию от посторонних глаз. Шифрование касается каждого человека, так как используется в создании электронной почты, банковских карт. Даже мобильная связь защищается кодами.
Кроме того, используются на системах, защищающих транспортные средства от угонщиков, создают преграду для атак вирусов и взломов компьютерных сайтов. При попытке продолжить разложение простых чисел или определить закономерность появления, возникают новые способы математических расчетов.
Математика предлагает начинать знакомиться с данными понятиями в средней школе, в 5 или в 6 классе.
Проверка на принадлежность к определенному множеству достаточно простая:
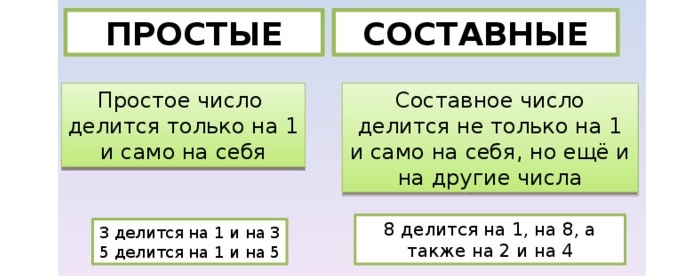
Простые числа можно делить только на 1 и на такое же число. Например 3 и 7 — простые числа, 3 делится на 1 и на 3, 7 делится на 1 и на 7.
Составные числа можно делить не только на себя и единицу. При этом не должно получаться остатка. Они делятся на одно или несколько значений. Например, 8 и 6 относят к составным. Восьмерка делится на 1, 2, 4, 8; шестерка – на 1, 2, 3 и 6.
Определение простых чисел позволяет исключить из их ряда единицу. Она характеризуется наличием только одного делителя, не являющегося отрицательным значением. Получить ее можно, используя только один способ, умножив саму на себя.
Простые двузначные числа определяются по внешнему виду:
Если оканчиваются четной цифрой, то точно являются составными. То же касается и значений, имеющих больше двух знаков.
Если на конце находится цифра 5, то она входит в число делителей.
Такие простые способы помогают легко классифицировать многозначные показатели.
Некоторые двузначные вводят в заблуждение с первого взгляда, если оканчиваются на единицу. Кажется, что разложить на множители их невозможно. Но есть исключения, например: 21, 81. Чем дальше, тем больше отклонений от этой закономерности.
Последовательность простых чисел
Есть целые алгоритмы, помогающие получать новое, ранее неизвестное значение.
Существуют таблицы, в которых собраны найденные числа, имеющие не больше двух делителей, например, до 200, 1000 или больше.
Последовательность можно продолжать бесконечно, начинается она так: 2, 3, 5, 7, 11, 13, 17, 19 и т. д.
Наименьшее и наибольшее простое число
Самым меньшим значением, делящимся на себя и 1, является 2. Это единственное простое значение, являющееся четным. Остальные всегда делятся на два, то есть получают третий делитель.
Простых чисел много и их количество стремится к бесконечности, потому узнать самое большое невозможно.
Нескончаемость ряда была доказана еще до нашей эры Евклидом. Он предложил перемножить все известные исследуемые значения и прибавить к ним единицу.
При его делении в любом случае будет оставаться остаток, то есть отнести к составным невозможно. Что противоречит тому факту, что были использованы все известные простые числа, в том числе и самое большое. Значит, предположение о конечности ряда является неверным.
В настоящее время известно значение, имеющее около 25 миллионов знаков. Оно относится к наибольшему из открытых наукой, это 2 82 589 933
Множество простых чисел
Множествами называются совокупности элементов, объединенных в одно целое общими свойствами.
Для изучаемых объектов к ним относятся:
принадлежность к натуральным;
наличие максимум двух делителей.
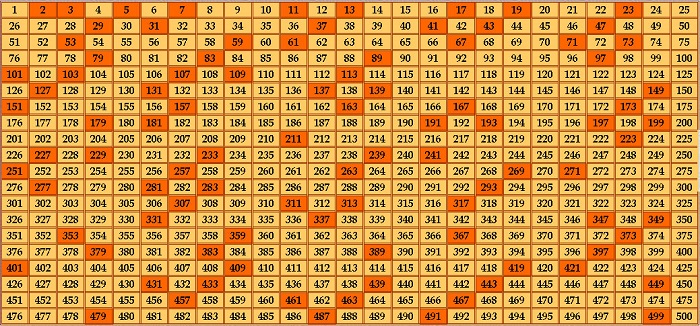
Простые числа можно определить, используя решето Эратосфена. Нужно выписать в ряд все значения, с которыми предстоит работать. Выбрать самое маленькое и вычеркнуть его, затем продолжать действие, убирая кратные ему.
Например, в ряду от 1 до 100 первым таким объектом будет 2. Поэтому и вычеркивать нужно значения, кратные двойке, то есть те, которые делятся на нее.
По окончании из оставшихся выбрать новое простое, искать кратные ему и также убирать. Повторять, пока это представляется возможным.
В итоге, все составные окажутся зачеркнутыми.
Эратосфен использовал свое открытие следующим образом. Он брал папирус, записывал на нем необходимые значения, при отборе прокалывал неподходящие острым предметом (отсюда название «решето Эратосфена»). Поэтому они как будто просеивались через сито, и в списке оставались видимыми только необходимые.
Некоторые свойства простых чисел
Выделяют свойства, объединенные в теоремы, постулаты. Многие являются основой математических правил, используемых в настоящее время.
Изучением занимается теория чисел, при использовании формул простые числа обозначаются буквой n.
Известны следующие правила:
Если рассматривать два простых числа (n), одно из которых делится на другое, то можно утверждать, что они равны.
Все являются нечетными, за исключением двойки.
Можно выделить пары, разница между которым равна 2. При их сложении получается значение, кратное трем. Их так и называют парными или близнецами. Исключение составляют две первые цифры в ряду, 3 и 5, так как сумму, полученную при их сложении, нельзя разделить на 3.
Для каждого натурального значения (N), большего единицы, существует n, превышающее его. При этом удвоенное натуральное будет больше n.
Если одно из двух N делится на n, то их произведение также будет делиться на него.
Любое N, за исключением единицы, можно отнести к n или представить в виде их произведения.
Если взять составное число и разложить его на множители n, то среди них окажется один, квадрат которого будет меньше первоначального составного.
Некоторые n имеют пары, которые можно найти, перевернув n наоборот. Например, 13 и 31, 37 и 73. То же самое касается трехзначных n: 107 и 701, 709 и 907.
Если N возвести в степень, представленную n, а затем вычесть N, то полученное значение будет делиться на используемое n. Это правило представляет собой малую теорему Ферма.
Действия с простыми числами
Можно использовать разные арифметические действия, складывать, умножать, вычитать, делить. Простые числа могут являться основанием и показателем степени.
Извлечь корень из них невозможно.
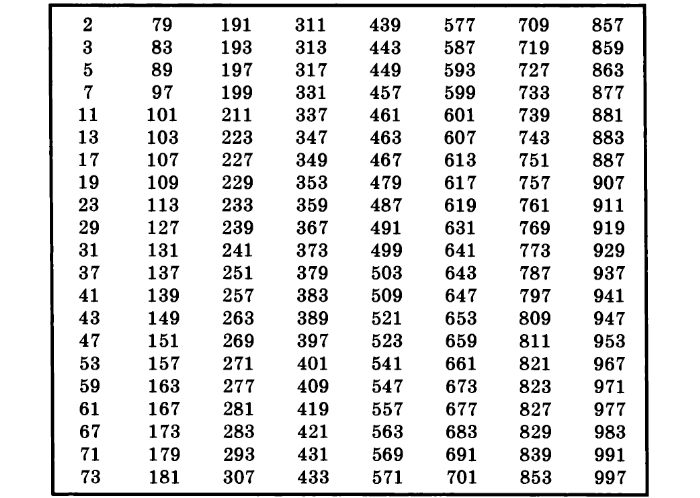
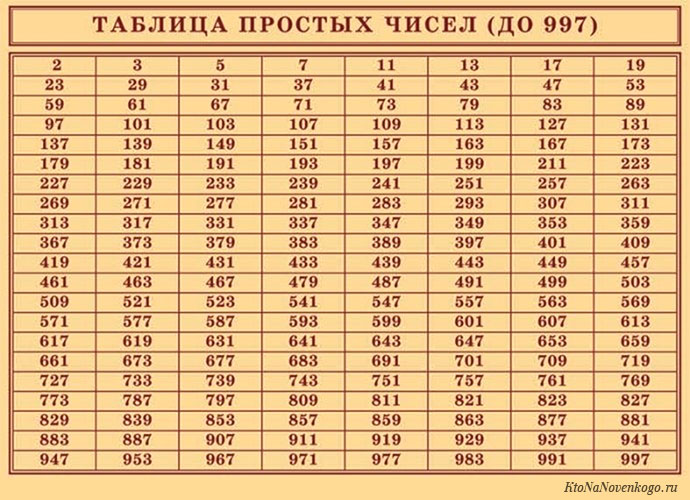
Таблица простых чисел до 1000
Таблица простых числе до 10000
Простые и составные числа
Основные определения
Натуральные числа больше единицы бывают простые и составные.
Простое число — это натуральное число больше 1, у которого есть всего два делителя: единица и само число.
Составное число — похоже на простое. Это точно такое же натуральное число больше единицы, которое делится на единицу, на само себя и еще хотя бы на одно натуральное число.
Число 1 — не является ни простым, ни составным числом, так как у него только один делитель — 1. Именно этим оно отличается от всех остальных натуральных чисел.
Число 2 — первое наименьшее простое, единственное четное, простое число. Все остальные — нечетные.
Число 4 — первое наименьшее составное число.
В математике есть первые простые и составные числа, но последних таких чисел не существует.
А еще не существует простых чисел, которые оканчиваются на 4, 6, 8 или 0. В числе простых есть только одно число, которое заканчивается на 2 — и это само число 2. Из оканчивающихся на 5 — число 5. Все остальные оканчиваются на 1, 3, 7 или 9, за исключением 21, 27, 33 и 39.
Таблица простых чисел до 1000
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 |
| 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 |
| 67 | 71 | 73 | 79 | 83 | 89 | 97 | 101 | 103 |
| 107 | 109 | 113 | 127 | 131 | 137 | 139 | 149 | 151 |
| 157 | 163 | 167 | 173 | 179 | 181 | 191 | 193 | 197 |
| 199 | 211 | 223 | 227 | 229 | 233 | 239 | 241 | 251 |
| 257 | 263 | 269 | 271 | 277 | 281 | 283 | 293 | 307 |
| 311 | 313 | 317 | 331 | 337 | 347 | 349 | 353 | 359 |
| 367 | 373 | 379 | 383 | 389 | 397 | 401 | 409 | 419 |
| 421 | 431 | 433 | 439 | 443 | 449 | 457 | 461 | 463 |
| 467 | 479 | 487 | 491 | 499 | 503 | 509 | 521 | 523 |
| 541 | 547 | 557 | 563 | 569 | 571 | 577 | 587 | 593 |
| 599 | 601 | 607 | 613 | 617 | 619 | 631 | 641 | 643 |
| 647 | 653 | 659 | 661 | 673 | 677 | 683 | 691 | 701 |
| 709 | 719 | 727 | 733 | 739 | 743 | 751 | 757 | 761 |
| 769 | 773 | 787 | 797 | 809 | 811 | 821 | 823 | 827 |
| 829 | 839 | 853 | 857 | 859 | 863 | 877 | 881 | 883 |
| 887 | 907 | 911 | 919 | 929 | 937 | 941 | 947 | 953 |
| 967 | 971 | 977 | 983 | 991 | 997 |
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Простые числа — это чудеса деления
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о таком математическом понятии, как ПРОСТЫЕ ЧИСЛА.
В школе это проходят в 5 или 6 классе, в зависимости от программы обучения.
И интересно, что если спросить школьников, что такое простые числа, то они, скорее всего, ответят правильно.
А вот взрослые задумаются и не факт, что вспомнят точное определение. Так что это статья скорее для них.
Простые числа — это.
Итак, вот как выглядит официальное определение:
Простые числа – это такие числа, которые имеют только два делителя. Один из них – единица, а другое – само число.
Чтобы было более понятно, приведем простой пример. Для чисел 5 и 7 надо найти все возможные делители, чтобы в результате образовалось целое число.
Если вы попробуете решить эту задачку, то получите, что 5 и 7 делятся только на 1 и 5, и 1 и 7 соответственно. Во всех других случаях вы получите дробное число. И это как раз означает, что числа 5 и 7 относятся к простым.
А вот попробуем по той же схеме разобрать числа 6 и 9. В первом случае мы получим, что 6 можно поделить на 1, 2, 3 и 6, а число 9 – на 1, 3 и 9. И это уже противоречит определению простых чисел, значит, 6 и 9 таковыми не являются.
Они называются в математике – СОСТАВНЫМИ ЧИСЛАМИ.
Список и таблица простых чисел
Некоторые ошибочно полагают, что наименьшее простое число – это единица.
С одной стороны, в этом есть логика, так как 1 делится только на 1. Но это получается одно и то же число (единица), что противоречит определению простых чисел, в котором четко прописано – «делителей должно быть два».
Значит, минимальное простое число – это 2. А первоначальный ряд выглядит следующим образом:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199…
При желании можете проверить эти числа на предмет деления. Мы же скажем, что этот ряд на самом деле не окончательный.
Количество простых чисел не ограничено. Или говоря математическим языком, оно стремится к бесконечности.
История простых чисел
Первые упоминания о простых числах относятся к Древнему Египту. В Британском музее хранится папирус, который датируется 2000 годом до нашей эры. И на нем, согласно расшифровке, содержится учебное пособие по арифметике.
В том числе и про деление чисел. Называется этот артефакт – папирус Райнда, по имени его первого владельца.
В этом документе есть таблица, в которой указаны числа, делящиеся на различные знаменатели. Причем они разделены таким образом, что становится понятно – древние египтяне может и не пользовались понятиям «простое число», но хотя бы имели о нем представление.
Ну а первые исследования простых чисел датируются 300 годом до нашей эры. И связаны они с именем знаменитого древнегреческого математика Евклида.
Как и многое другое, он описал простые и составные числа в своем известном произведении «Начала».
В частности, Евклид описал такие вещи, как:
Сейчас расскажем об этих понятиях подробнее.
Основная теорема арифметики
Основная теорема арифметики, которую придумал еще Евклид, гласит:
Любое натуральное число (это что?), которое больше единицы, может быть представлено в виде произведения простых чисел. Причем их количество не ограничено, а порядок следования неважен.
Если обозначить исходное число буквой N, а простые числа буквами Р1, Р2, Р3 и так далее, то можно записать эту теорему следующим образом:
N = Р1 * Р2 * Р3 * … * РК
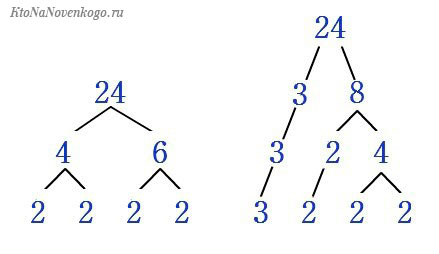
Например, возьмем число 100. Его можно разложить на следующие простые числа:
Или более сложный пример – число 23244:
23244 = 149 * 13 * 3 * 2 * 2
Раскладывать на простые числа легко. Можно сперва делить на 2 и 3, а уже в конце автоматически получить более сложные делители.
Ради интереса придумайте любое число и сами найдите его составляющие.
Лемма Евклида
Еще одна теорема, которая имеет прямое отношение к простым числам. Она гласит;
Если некое простое число Р делит произведение чисел X и Y без остатка, то оно может точно так же поделить или X, или Y.
Звучит несколько сложновато, хотя на деле все это просто. Так, возьмем для примера P = 2, X = 6, Y = 9. И тогда получается, что
В нашем примере P делит это произведение без остатка:
А значит наша P может поделить без остатка или X, или Y. Очевидно, что это X:
Y/P = 9/2 = 4,5 (не подходит)
Как быстро и легко определить простые числа
И еще одно понятие, которое связано с простыми числами. Оно названо в честь другого древнегреческого математика Эратосфена Киренского.
Этот человек придумал, как быстро и легко определить простые числа. В частности, он сделал таблицу, в которой были указаны значения до 1000.
Свою таблицу он нарисовал на глиняной дощечке. А после прокалывал те клеточки, на которых были написаны составные числа. В результате получилось нечто вроде решета, отсюда собственно и название метода.
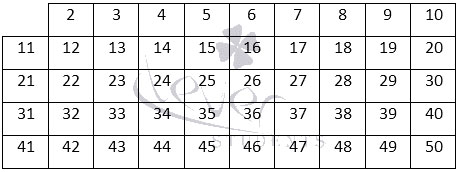
Кстати, пользоваться решетом Эратосфена весьма просто. Например, сделаем таблицу до 50.
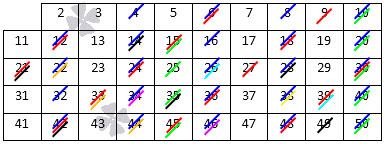
После этого из нее надо поочередно вычеркивать числа, которые кратны 2, 3, 5, 7 и 11. В результате получится вот это:
Те числа, которые остались, и есть простые. Можете сравнить этот ряд с тем, который мы давали в начале статьи. Точно таким же способом можно составить абсолютно любой ряд простых чисел = хоть до тысячи, хоть до миллиона и больше.
Вот и все, что мы хотели рассказать о ПРОСТЫХ ЧИСЛАХ в математике.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
Математика весьма хитрая наука, да и простые числа не такие уж и простые, понимание простых и составных чисел привело человечество к тому техническому прогрессу, что окружает нас сейчас.
Что такое Простые числа
Простые числа — это натуральные числа, больше единицы, которые делятся без остатка только на 1 и на само себя. Например: 2, 3, 5, 7, 11, 13, 17, 19, 23. Единица не является ни простым числом, ни составным.
Последовательность простых чисел начинается с 2 и является бесконечной; наименьшее простое число — это 2 (делится на 1 и на самого себя).
Составные числа — это натуральные числа, у которых есть больше двух делителей (1, оно само и например, 2 и/или 3); это противоположность простым числам. Например: 4, 6, 9, 12 (все делятся на 2, на 3, на 1 и на само себя).
Все натуральные числа считаются либо простыми, либо составными (кроме 1).
Натуральные числа — это те числа, которые возникли натуральным образом при счёте предметов; например: 1, 2, 3, 4. (нет ни дробей, ни 0, ни чисел ниже 0).
Зачастую множество простых чисел в математике обозначается буквой P.