Простое высказывание а истинно а высказывание в ложное что можно
Простое высказывание а истинно а высказывание в ложное что можно
Простые и сложные высказывания, логические переменные и логические константы, логическое отрицание, логическое умножение, логическое сложение, таблицы истинности для логических операций
Для описания рассуждений и правил выполнения действий с информацией используют специальный язык, принятый в математической логике. В основе рассуждений содержатся специальные предложения, называемые высказываниями. В высказываниях всегда что-либо утверждается или отрицается об объектах, их свойствах и отношениях между объектами. Высказыванием является любое суждение, относительно которого можно сказать, истинно оно или ложно. Высказываниями могут быть только повествовательные предложения. Вопросительные или побудительные предложения высказываниями не являются.
Высказывание — суждение, сформулированное в виде повествовательного предложения, о котором можно сказать, истинно оно или ложно.
Например, вопросительные предложения «В каком году было первое летописное упоминание о Москве?» и «Что является внешней памятью компьютера?» или побудительное предложение «Соблюдайте правила техники безопасности в компьютерном классе» высказываниями не являются. Повествовательные предложения «Первое летописное упоминание о Москве было в 1812 г.», «Оперативное запоминающее устройство является внешней памятью компьютера» и «В компьютерном классе не надо соблюдать правила техники безопасности» являются высказываниями, поскольку это суждения, о каждом из которых можно сказать, что оно ложно. Истинными высказываниями будут суждения «Первое летописное упоминание о Москве было в 1147 г.», «Жесткий магнитный диск является внешней памятью компьютера».
Каждому высказыванию соответствует только одно из двух значений: или «истина», или «ложь», которые являются логическими константами. Истинное значение принято обозначать цифрой 1, а ложное значение — цифрой 0. Высказывания можно обозначать с помощью логических переменных, в качестве которых используются заглавные латинские буквы. Логические переменные могут принимать только одно из двух возможных значений: «истина» или «ложь». Например, высказывание «Информация в компьютере кодируется с помощью двух знаков» можно обозначить логической переменной А, а высказывание «Принтер является устройством хранения информации» можно обозначить логической переменной В. Поскольку первое высказывание соответствует действительности, то А = 1. Такая запись означает, что высказывание А истинно. Так как второе высказывание не соответствует действительности, то В = 0. Такая запись означает, что высказывание в ложно.
Высказывания могут быть простыми и сложными. Высказывание называется простым, если никакая его часть не является высказыванием. До сих пор были приведены примеры простых высказываний, которые обозначались логическими перемены ми. Выстраивая цепочку рассуждений, человек с помощью логических операций объединяет простые высказывания в сложнее’ высказывания. Чтобы узнать значение сложного высказывания нет необходимости вдумываться в его содержание. Достаточно знать значение простых высказываний, составляющих сложное высказывание, и правила выполнения логических операций.
Логическая операция — действие, позволяющее составлять сложное высказывание из простых высказываний.
Все рассуждения человека, а также работа современных технических устройств основываются на типовых действиях с информацией — трех логических операциях: логическом отрицании (инверсии), логическом умножении (конъюнкции) и логическом сложении (дизъюнкции).
Логическое отрицание простого высказывания получают добавлением слов «Неверно, что» в начале простого высказывания.
■ ПРИМЕР 1. Имеется простое высказывание «Крокодилы умеют летать». Результатом логического отрицания будет высказывание «Неверно, что крокодилы умеют летать». Значение исходного высказывания — «ложь», а значение нового — «истина».
■ ПРИМЕР 2. Имеется простое высказывание «Файл должен иметь имя». Результатом логического отрицания будет высказывание «Неверно, что файл должен иметь имя». Значение исходного высказывания — «истина», а значение нового высказывания — «ложь».
Можно заметить, что логическое отрицание высказывания истинно, когда исходное высказывание ложно, и наоборот, логическое отрицание высказывания ложно, когда исходное высказывание истинно.
Логическое отрицание (инверсия) — логическая операция, ставящая в соответствие простому высказыванию новое высказывание, значение которого противоположно значению исходного высказывания.
Обозначим простое высказывание логической переменной А. Тогда логическое отрицание этого высказывания будем обозначать НЕ А. Запишем все возможные значения логической переменной А и соответствующие результаты логического отрицания НЕ А в виде таблицы, которая называется таблицей истинности для логического отрицания (табл. 40).
ТАБЛИЦА ИСТИННОСТИ ДЛЯ ЛОГИЧЕСКОГО ОТРИЦАНИЯ
Если/1 = 0, то НЕ А = 1 (см. пример 1).
Если А = 1, то НЕ А = 0 (см. пример 2)
Можно заметить, что в таблице истинности для логического отрицания ноль меняется на единицу, а единица меняется на ноль.
Логическое умножение двух простых высказываний получают объединением этих высказываний с помощью союза и. Разберем на примерах 3—6, что будет являться результатом логического умножения.
■ ПРИМЕР 3. Имеются два простых высказывания. Одно высказывание — «Карлсон живет в подвале». Другое высказывание — «Карлсон лечится мороженым».
Результатом логического умножения этих простых высказываний будет сложное высказывание «Карлсон живет в подвале, и Карлсон лечится мороженым». Можно сформулировать новое высказывание более кратко: «Карлсон живет в подвале и лечится мороженым». Оба исходных высказывания ложны. Значение нового сложного высказывания также «ложь».
■ ПРИМЕР 4. Имеются два простых высказывания. Первое высказывание — «Карлсон живет в подвале». Второе высказывание — «Карлсон лечится вареньем».
Результатом логического умножения этих простых высказываний будет сложное высказывание «Карлсон живет в подвале и лечится вареньем». Первое исходное высказывание ложно, а второе истинно. Значение нового сложного высказывания — «ложь».
■ ПРИМЕР 5. Имеются два простых высказывания. Первое высказывание — «Карлсон живет на крыше». Второе высказывание — «Карлсон лечится мороженым».
Результатом логического умножения этих простых высказываний будет сложное высказывание «Карлсон живет на крыше и лечится мороженым». Первое исходное высказывание истин но, а второе ложно. Значение нового сложного высказывания «ложь».
Результатом логического умножения этих простых высказываний будет сложное высказывание «Карлсон живет на крыше и лечится вареньем». Оба исходных высказывания истинны. Зпачение нового сложного высказывания также «истина».
Можно заметить, что логическое умножение двух высказываний истинно только в одном случае — когда оба исходных высказывания истинн ы.
Логическое умножение (конъюнкция) — логическая операция, ставящая в соответствие двум простым высказываниям новое высказывание, значение которого истинно тогда и только тогда, когда оба исходных высказывания истинны.
ТАБЛИЦА ИСТИННОСТИ ДЛЯ ЛОГИЧЕСКОГО УМНОЖЕНИЯ
Простое высказывание а истинно а высказывание в ложное что можно

2. Построение таблиц истинности и логических функций.
3. Законы логики и преобразование логических выражений.
Лабораторная работа № 3. Основы математической логики.

Исследования в алгебре логики тесно связаны с изучением высказываний (хотя высказывание — предмет изучения формальной логики). Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель).
Простым высказыванием называют повествовательное предложение, относительно которого имеет смысл говорить, истинно оно или ложно.
Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.
Высказывания 1 и 3 являются истинными. Высказывание 2 – ложным , потому что число 27 составное 27=3*3*3.
Итак, отличительным признаком высказывания является свойство быть истинным или ложным, последние четыре предложения этим свойством не обладают.
С помощью высказываний устанавливаются свойства, взаимосвязи между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно ложно.
Однако определение истинности высказывания далеко не простой вопрос. Например, высказывание «Число 1 +22 = 4294 967297 — простое», принадлежащее Ферма (1601-1665), долгое время считалось истинным, пока в 1732 году Эйлер (1707-1783) не доказал, что оно ложно. В целом, обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания «Сумма углов треугольника равна 180°» устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным.
В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно. Обозначаются логические переменные, большими буквами латинского алфавита.
Существуют разные варианты обозначения истинности и ложности логических переменных:
Сложные (составные) высказывания представляют собой набор простых высказываний (по крайней мере двух) связанных логическими операциями.
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением).
Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение.
Введем перечисленные логические операции.
В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.
Основы алгебры логики
Основные понятия и аксиомы алгебры логики. Простые и сложные высказывания.
Исследования в алгебре логики тесно связаны с изучением высказываний, вызвано это тем, что высказывания являются одним из основных видов носителей информации. С помощью высказываний мы устанавливаем свойства, взаимосвязи между объектами.
Примерами высказываний на естественном языке являются предложения: « Сегодня светит солнце » или « На Красной площади зимой 2007–2008 гг. заливали каток ». Каждое из этих высказываний характеризует свойства или состояние конкретного объекта. Каждое высказывание несет значение « истина » или « ложь ».
Определение. Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности.
Это определение не является математически точным.
Более того, только на первый взгляд оно кажется удовлетворительным. Это определение породило много логических парадоксов.
Причина этого парадокса лежит в структуре построения указанного предложения : оно ссылается на свое собственное значение. С помощью определенных ограничений на допустимые формы высказываний могут быть устранены такие ссылки на себя, и, следовательно, устранены возникающие отсюда парадоксы.
Интересную задачу, содержащую парадокс, придумал знаменитый математик « Известно, что в некотором городе брадобрей бреет всех тех и только тех жителей города, которые не бреются сами. Кто бреет брадобрея? »
Определение. Высказывание называется простым (элементарным), если никакая его часть сама не является высказыванием.
Алгебра логики отвлекается от смысловой содержательности высказываний. Мы можем договориться, что абсурдное по смыслу высказывание: « Крокодилы летают » – является истинным, и с этим значением высказывания будем работать.
Введение таких ограничений дает возможность изучать высказывания алгебраическими методами, т.е. позволяет ввести операции над элементарными высказываниями и с их помощью строить и изучать составные высказывания.
Употребляемые в русском языке связки « и », « или », « не », « если…, то… », « тогда и только тогда, когда … » позволяют из уже заданных высказываний строить новые, более « сложные » высказывания.
Определение. Сложное высказывание – это высказывание, которое состоит из двух или более простых высказываний, объединенных логическими связками.
В алгебре логики логическая операция полностью задается таблицей истинности, указывающей, какие значения принимает сложное высказывание при всех возможных значениях простых высказываний, входящих в сложное высказывание.
Логические операции и соответствующие им логические связки имеют специальные названия и обозначаются следующим образом:
Простые и составные высказывания
Есть два вида высказываний: 1) простые и 2) составные, или сложные.
Под простым высказыванием будем понимать такое высказывание, которое не может быть разбито на более простые высказывания. Высказывания А и В предыдущего примера – простые высказывания.
Про простое высказывание всегда однозначно можно сказать, что оно истинно или ложно, не интересуясь его структурой.
Из простых высказываний при помощи так называемых логических связок или логических операций, например, союзов «и», «или», слов «если…, то…», «тогда и только тогда, когда…», можно строить сложные высказывания.
Например, из высказываний 




Отметим, что сложные высказывания можно образовывать и из таких высказываний, которые не связаны между собой по смыслу. Например, высказывание:
составлено при помощи логической операции «если…, то…» из двух высказываний, между которыми нет никакой смысловой связи.
Сложные высказывания, как и простые, всегда или только истинны, или только ложны. Истинность или ложность сложного высказывания полностью определяется, во-первых, тем, какие логические связки (операции) использованы для образования сложного высказывания. Во-вторых, истинность или ложность сложного высказывания определяется тем, какие из простых высказываний, образующих сложное высказывание, истинны, а какие – ложны.
Логические операции
Операции над высказываниями – логические операции – обычно задают в виде таблиц, называемых таблицами истинности.
Операция отрицания, или отрицание высказывания
Для каждого высказывания А может быть сформировано новое высказывание 

Таблица истинности для операции отрицания:
| А |  |
Операция отрицания – одноместная, или унарная, операция.
Последующие операции – двухместные, или бинарные.
Например, если 

Отметим, что если 

Операция конъюнкции, или конъюнкция высказываний
Высказывание С, составленное из двух высказываний А и В при помощи союза «и», называют конъюнкцией (логическим произведением) этих высказываний: 

Логическое произведение 
Таблица истинности для операции конъюнкции:
| А | В |  |
Пусть, например, 

Операцию конъюнкции можно определить и для нескольких высказываний, как связку высказываний, объединённых союзом «и». Конъюнкция из n высказываний – новое высказывание, причём высказывание
А = 
имеет значение «истина», если и А1, и А2, и … Аn одновременно истинны. Во всех других случаях эта конъюнкция имеет значение «ложь».
Пусть, например, А1 



А2 Ù А3 Ù А4 
А1 Ù А3 Ù А4 
Операция дизъюнкции, или дизъюнкция высказываний
Высказывание С, составленное из двух высказываний А, В при помощи союза «или», называют дизъюнкцией (логической суммой) этих высказываний: 

Сумма 
Таблица истинности для операции дизъюнкции:
| А | В |  |
Пусть, например, 



Операцию дизъюнкции можно определить и для нескольких высказываний как связку высказываний, объединённых союзом «или»:
А = 
В этом случае высказывание А истинно, если истинно хотя бы одно из высказываний, входящих в связку.
Операция эквивалентности, или эквивалентность высказываний.
Высказывание С, составленное из двух высказываний А и В при помощи слов «тогда и только тогда, когда…», называют эквивалентностью высказываний А и В: 
Для эквивалентности используют знак 
Таблица истинности для операции эквивалентности:
| А | В |  |
Пусть 

Высказывание 

Операция импликации, или импликация высказываний
Высказывание С, составленное из высказываний А и В при помощи слов «если…, то…», называют импликацией высказываний А и В и 1б1-начают
(выражение 
Импликация 
Таблица истинности для операции импликации:
| А | В |  |
Первый член импликации 
Обратите внимание, что таблица истинности для импликации, в отличии от таблиц для конъюнкции, дизъюнкции и эквивалентности, изменяется при перестановке столбцов для А и В.
Отметим также, что импликация не полностью соответствует обычному пониманию слов «если…, то…» и «следует». Из третьей и четвёртой строк таблицы истинности для импликации вытекает, что если А – ложно, то, каково бы ни было В, высказывание 
Например, утверждение «если 6 – простое число, то 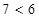
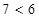
Как говорил Р. Декарт: «Если 2 х 2 = 5, то я докажу, что из трубы вылетает ведьма».
Для иллюстрации содержательного смысла импликации рассмотрим ещё один пример.
Пусть 

Импликация 
«если папа завтра получит премию, то купит сыну велосипед».
Пусть А и В – истинны. Тогда папа, получив премию, покупает сыну велосипед. Естественно считать это истинным высказыванием.
Если же папа, получив премию (А – истинно), не купит сыну велосипед (В – ложно), то это, можно сказать, – не логичный поступок, и импликация имеет значение «ложь».
Если папа не получит премию (А – ложно), но купит велосипед (В – истинно), то результат положителен (импликация истинна).
Наконец, в том случае, если, не получив премии (А – ложно), папа не купит велосипед (В – ложно), то обещание не нарушено, импликация истинна.
Задача 1. Даны два высказывания 





1) Высказывание 
2) Высказывание 
Высказывание 

3) Эквивалентность ( 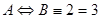

4) Импликация 

В самом деле, импликация 

