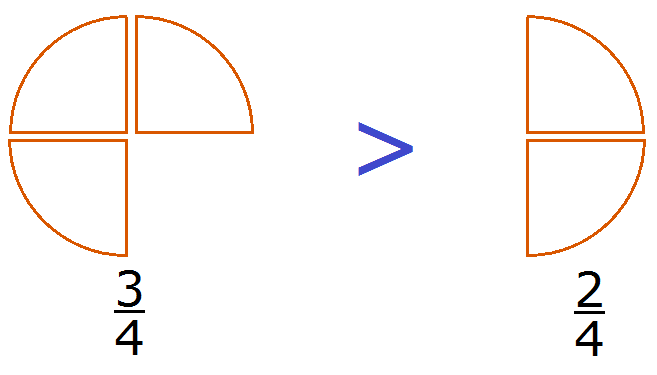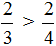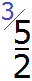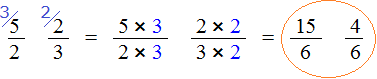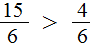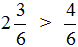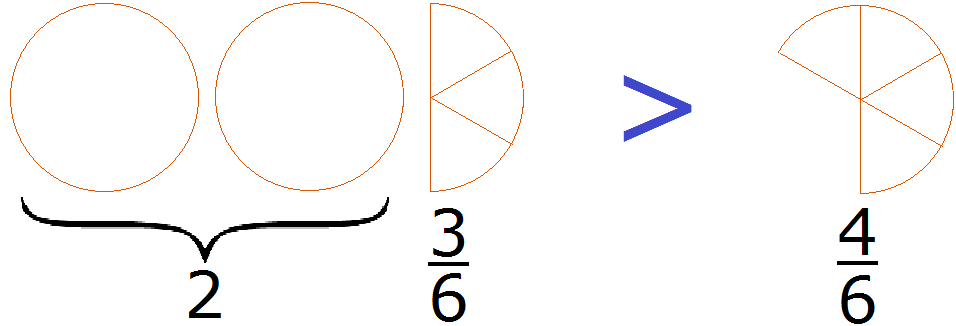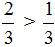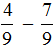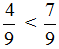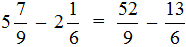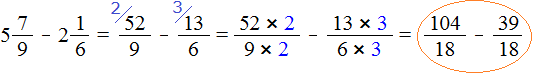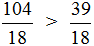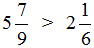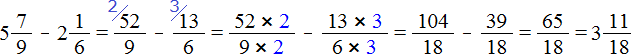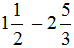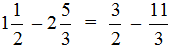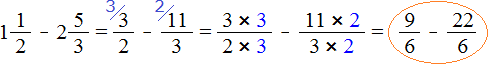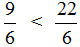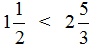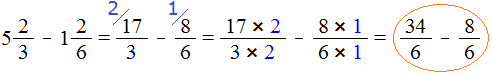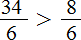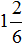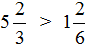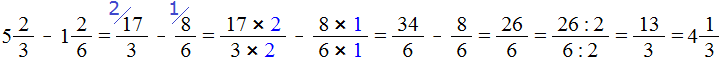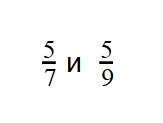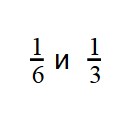Промежуточное число при сравнении дробей что это такое

Сравнение дробей: правила, примеры, решения

Данная статья рассматривает сравнение дробей. Здесь мы выясним, какая из дробей больше или меньше, применим правило, разберем примеры решения. Сравним дроби как с одинаковыми, так и разными знаменателями. Произведем сравнение обыкновенной дроби с натуральным числом.

Сравнение дробей с одинаковыми знаменателями

Отсюда следует правило сравнения дробей с одинаковыми знаменателями: из имеющихся дробей с одинаковыми показателями считается большей та дробь, у которой числитель больше и наоборот.

Это говорит о том, что следует обратить внимание на числители. Для этого рассмотрим пример.

Сравнение дробей с разными знаменателями

Сравнение таких дробей можно соотнести со сравнением дробей с одинаковыми показателями, но имеется различие. Теперь необходимо дроби приводить к общему знаменателю.

Если имеются дроби с разными знаменателями, для их сравнения необходимо:

Рассмотрим данные действия на примере.

Ответ: 5 18 > 23 86 .

Сравнение дробей с одинаковыми числителями

Если дроби имеют одинаковые числители и разные знаменатели, тогда можно выполнять сравнение по предыдущему пункту. Результат сравнения возможет при сравнении их знаменателей.

Имеется правило сравнения дробей с одинаковыми числителями: из двух дробей с одинаковыми числителями больше та дробь, которая имеет меньший знаменатель и наоборот.

Рассмотрим на примере.

Решение

Сравнение дроби с натуральным числом

Источник

Сравнение дробей

Продолжаем изучать дроби. Сегодня мы поговорим об их сравнении. Тема интересная и полезная. Она позволит новичку почувствовать себя учёным в белом халате.

Суть сравнения дробей заключается в том, чтобы узнать какая из двух дробей больше или меньше.

Чтобы ответить на вопрос какая из двух дробей больше или меньше, пользуются операциями отношения, такими как больше (>) или меньше ( )

Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на четыре части. 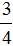пиццы больше, чем пиццы:

Каждый согласится с тем, что первая пицца больше, чем вторая.

Сравнение дробей с одинаковыми числителями

Следующий случай это когда числители дробей одинаковые, но знаменатели разные. Для таких случаев предусмотрено следующее правило:

Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше. И соответственно меньше та дробь, у которой знаменатель больше.

Например, сравним дроби и . У этих дробей одинаковые числители. У дроби знаменатель меньше, чем у дроби . Значит дробь больше, чем дробь . Так и отвечаем:

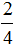
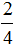
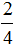
Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на три и четыре части. пиццы больше, чем пиццы:

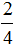
Каждый согласится с тем, что первая пицца больше, чем вторая.

Сравнение дробей с разными числителями и разными знаменателями

Чтобы ответить на вопрос, какая из этих дробей больше или меньше, нужно привести их к одинаковому (общему) знаменателю. Затем можно будет легко определить какая дробь больше или меньше.

Приведём дроби и к одинаковому (общему) знаменателю. Найдём наименьшее общее кратное (НОК) знаменателей обеих дробей. НОК знаменателей дробей и это число 6.

Теперь находим дополнительные множители для каждой дроби. Разделим НОК на знаменатель первой дроби . НОК это число 6, а знаменатель первой дроби это число 2. Делим 6 на 2, получаем дополнительный множитель 3. Записываем его над первой дробью:

Умножим дроби на свои дополнительные множители:

Мы пришли к тому что дроби, у которых были разные знаменатели, превратились в дроби, у которых одинаковые знаменатели. А как сравнивать такие дроби мы уже знаем. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше:

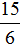
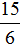
Правило правилом, а мы попробуем разобраться почему больше, чем . Для этого выделим целую часть в неправильной дроби . В дроби ничего выделять не нужно, поскольку эта дробь уже правильная.

После выделения целой части в дроби 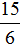, получим следующее выражение:

Теперь можно легко понять, почему 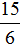больше, чем . Давайте нарисуем эти дроби в виде пицц:

2 целые пиццы и пиццы, больше чем пиццы.

Вычитание смешанных чисел. Сложные случаи.

Вычитая смешанные числа иногда можно обнаружить, что всё идёт не так гладко как хотелось бы.

При вычитании чисел уменьшаемое должно быть больше вычитаемого. Только в этом случае будет получен нормальный ответ.

Уменьшаемое 10 больше вычитаемого 8, поэтому мы получили нормальный ответ 2.

А теперь посмотрим, что будет если уменьшаемое окажется меньше вычитаемого. Пример 5 − 7 = −2

В этом случае мы выходим за пределы привычных для нас чисел и попадаем в мир отрицательных чисел, где нам ходить пока рано, а то и опасно. Чтобы работать с отрицательными числами, нужна соответствующая математическая подготовка, которую мы ещё не получили.

Если при решении примеров на вычитание вы обнаружите, что уменьшаемое меньше вычитаемого, то можете пока пропустить такой пример. Работать с отрицательными числами допустимо только после их изучения.

С дробями ситуация та же самая. Уменьшаемое должно быть больше вычитаемого. Только в этом случае можно будет получить нормальный ответ. А чтобы понять больше ли уменьшаемая дробь, чем вычитаемая, нужно уметь сравнить эти дроби.

Например, решим пример .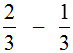

Это пример на вычитание. Чтобы решить его, нужно проверить больше ли уменьшаемая дробь, чем вычитаемая. больше чем

поэтому смело можем вернуться к примеру и решить его:

Теперь решим такой пример

Проверяем больше ли уменьшаемая дробь, чем вычитаемая. Обнаруживаем, что она меньше:

В этом случае разумнее остановиться и не продолжать дальнейшее вычисление. Вернёмся к этому примеру, когда изучим отрицательные числа.

Смешанные числа перед вычитанием тоже желательно проверять. Например, найдём значение выражения .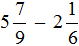

Сначала проверим больше ли уменьшаемое смешанное число, чем вычитаемое. Для этого переведём смешанные числа в неправильные дроби:

Получили дроби с разными числителями и разными знаменателями. Чтобы сравнить такие дроби, нужно привести их к одинаковому (общему) знаменателю. Не будем подробно расписывать как это сделать. Если испытываете затруднения на этом моменте, обязательно изучите действия с дробями.

После приведения дробей к одинаковому знаменателю, получаем следующее выражение:

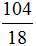
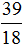
Теперь нужно сравнить дроби и . Это дроби с одинаковыми знаменателями. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.

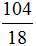
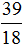
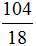
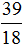
У дроби числитель больше, чем у дроби . Значит дробь больше, чем дробь .

А это значит что уменьшаемое 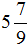больше, чем вычитаемое

А значит мы можем вернуться к нашему примеру и смело решить его:

Пример 3. Найти значение выражения

Проверим больше ли уменьшаемое, чем вычитаемое.

Переведём смешанные числа в неправильные дроби:

Получили дроби с разными числителями и разными знаменателями. Приведем данные дроби к одинаковому (общему) знаменателю:

Теперь сравним дроби и . У дроби числитель меньше, чем у дроби , значит дробь меньше, чем дробь

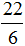
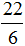
А это значит, что и уменьшаемое 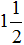меньше, чем вычитаемое

А это гарантировано приведёт нас в мир отрицательных чисел. Поэтому разумнее остановиться на этом месте и не продолжать вычисление. Продолжим его после изучения отрицательных чисел.

Пример 4. Найти значение выражения

Проверим больше ли уменьшаемое, чем вычитаемое.

Переведём смешанные числа в неправильные дроби:

Получили дроби с разными числителями и разными знаменателями. Приведем их к одинаковому (общему) знаменателю:

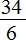
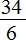
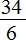
Теперь нужно сравнить дроби и . У дроби числитель больше, чем у дроби . Значит дробь больше, чем дробь .

А это значит, что уменьшаемое 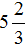больше, чем вычитаемое

Поэтому мы смело можем продолжить вычисление нашего примера:

Сначала мы получили ответ . Эту дробь мы сократили на 2 и получили дробь , но такой ответ нас тоже не устроил и мы выделили целую часть в этом ответе. В итоге получили ответ .

Источник

Сравнение дробей: как правильно

Сравнение дробей с одинаковыми знаменателями

Как и при любом другом сравнении, суть сравнения дробей — в том, чтобы определить меньшую и большую дроби.

Нет ситуации более благоприятной для сравнения, чем дроби с одинаковыми знаменателями. Если вся разница между дробями только в числителях, пользуемся следующим правилом:

Из двух дробей с одинаковыми знаменателями больше дробь с большим числителем. А меньше будет та дробь, числитель которой меньше.

А теперь на примерах.

Пример 1. Сравните дроби:

Пример 3. Сравните дроби:

Как видите, нет ничего сложного в сравнении дробей, если знаменатели равны. Вся задача заключается в том, чтобы определить больший и меньший числитель.

Давайте разберем наглядный пример сравнения дробей. Еще больше наглядных примеров — на курсах по математике в онлайн-школе Skysmart!

Допустим, в торте 6 кусков. Если от целого торта отрезать один кусок — в торте останется 5 кусков.

Понять, что целый торт больше, чем торт без одного куска, можно и без сравнения дробей. Но это же самое правило можно применить и при менее очевидных сравнениях, которые часто встречаются в повседневной жизни.

Сравнение дробей с одинаковыми числителями

Вы уже разобрались со сравнением дробей с одинаковыми знаменателями. Теперь задача чуть усложняется — научимся сравнивать дроби с разными знаменателями, но с одинаковыми числителями.

Если у двух дробей одинаковые числители, то больше будет та дробь, чей знаменатель меньше. А меньше будет дробь с большим знаменателем.

А теперь наши любимые примеры. Погнали!

Пример 1. Сравните дроби:

Пример 3. Сравните дроби:

Сравнение дробей с разными числителями и разными знаменателями

Нет ничего хитрого в сравнении дробей с одинаковыми числителями или знаменателями. Чуть больше усилий потребуется при сравнении дробей, в которых нет ничего одинакового.

Сначала вспомним, как привести дроби к общему знаменателю.
Рассмотрим пример дробей с разными знаменателями.

Давайте потренируемся в сравнении дробей.

Пример 1. Сравните дроби:

При сравнении неправильных дробей с правильными помните, что неправильная дробь всегда больше правильной.

Пример 2: Сравните дроби:

Вычитание смешанных чисел

Вычитание проходит гладко, когда уменьшаемое больше вычитаемого.

В случае, если вычитаемое больше уменьшаемого, разность оказывается отрицательной. В этом нет ничего страшного. Но математика в 5 классе — «положительная», поэтому научимся находить разность смешанных чисел, не скатываясь «в минусы».

При вычитании дробей действует тот же самый принцип: вычитаемое должно быть меньше уменьшаемого. Вот здесь то вам и пригодится навык сравнивать дроби.

Пример 1. Вычислите:

Вычитаемая дробь меньше уменьшаемой

Пример 2.Найдите разность:

Примеры для самопроверки

Теория — это, конечно, хорошо. Но без практики — никуда. Пора потренироваться в решении примеров и закрепить тему сравнения дробей.

Пример 1. Сравните дроби:

Ответ: по правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, у которой числитель больше. Это значит, что

Пример 2. Сравните дроби:

Ответ: по правилу сравнения дробей с разными знаменателями и одинаковыми числителями, больше та дробь, чей знаменатель меньше. Это значит, что

Пример 3. Сравните дроби:

Ответ:.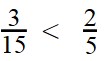

Источник

Разные способы сравнения дробей

Конспект урока математики в 5 классе. Тип урока: ОНЗ.

Просмотр содержимого документа
«Разные способы сравнения дробей»

Урок математики в 5 классе

Тема: «Разные способы сравнения дробей»

Учитель: В.В. Ермоленко, МОУ средняя школа №52 г. Ярославль

Повторить и закрепить изученные правила сравнения дробей: сравнения дробей с одинаковыми числителями, с одинаковыми знаменателями, приведение дробей к общему знаменателю;

Сформировать способность к построению и применению алгоритма сравнения дробей с помощью сравнения с 1, сравнения дополнений до 1 и с помощью сравнения с промежуточным числом.

1. Мотивация к учебной деятельности.

Цель этапа: включить учащихся в учебную деятельность, определить содержательные рамки урока.

Организация учебного процесса на этапе 1:

— Ребята, с множеством каких чисел мы работаем?

(С множеством дробных чисел)

-Чему вы уже научились?

(Мы научились приводить дроби у общему знаменателю, сравнивать дроби с разными числителями и разными знаменателями, с равными числителями и равными знаменателями)

— Правильно. Но есть еще способы сравнения дробей. Хотите узнать эти способы

-Значит, вперед за новыми знаниями. И работать мы будем дружно и успешно, как всегда. Новые знания строятся всегда на хорошо усвоенных старых умения и знания. Поэтому, наш урок открытия новых знаний мы начнем с повторения

2. Актуализация знаний и фиксация затруднения в деятельности.

1) актуализировать учебное содержание, необходимое и достаточное для восприятия нового материала: основное свойство дроби, правильные и неправильные дроби, приведение дробей к одинаковому знаменателю, к одинаковому числителю;

2) актуализировать мыслительные операции, необходимые и достаточные для восприятия нового материала: сравнение, анализ, обобщение;

3) зафиксировать все повторяемые понятия и алгоритмы в виде схем и символов: в виде свойств и определения;

4) зафиксировать индивидуальное затруднение в деятельности, демонстрирующее на личностно значимом уровне недостаточность имеющихся знаний: сравнить дроби, у которых разные знаменатели и разные числители.

Организация учебного процесса на этапе 2:

-Предлагаю сравнить дроби и назвать основные алгоритмы, которые вы применяли.

(Учащиеся устно сравнивают дроби, проговаривая правило, которое применяют для сравнения. Правило в виде эталона фиксируется на доске)

1) и ; 3) и ; 5) и ;

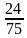
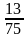
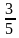
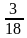
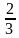
2) и 4) и ; 6) и ;

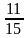
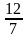
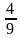
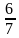
Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше

, если а с

, если а

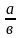
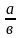
Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше

, если в

, если в с

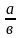
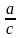
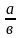
Основное свойство дроби: = ; =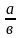

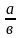
-Вы хорошо справились, т.к. знаете правила сравнения

Предлагаю сравнить дроби в течении 1 минуты:

и ; и ; и

_ Кто выполнил задание?

(Выполнивших задание нет)

3. Выявление причин затруднения и постановка цели деятельности.

1) организовать коммуникативное взаимодействие, в ходе которого выявляется и фиксируется отличительное свойство задания, вызвавшего затруднение в учебной деятельности;

2) согласовать цель и тему урока.

Организация учебного процесса на этапе 3:

— Почему нет результата?

(Трудно считать по известным правилам, мало времени)

— Что у вас не получилось?

(Не получилось быстро сравнить предложенное дроби)

(Мы применяли известные способы сравнения дробей, но их трудно применить к данным дробям)

-Что вы предлагаете в этой ситуации?

(Придумать новые способы сравнения дробей)

— Значит, вы предполагаете, что существуют и другие способы сравнения дробей. ( Да)

-Какая цель нашего урока?

(Найти способы сравнения, в которых не надо приводить дроби к общему знаменателю или одинаковому числителю)

— Значит, существуют и другие способы сравнения дробей Сформулируйте тему урока.

(Различные способы сравнения дробей)

— Запишем тему в тетради

4. Построение проекта выхода из затруднения.

организовать коммуникативное взаимодействие для построения нового способа действия, устраняющего причину выявленного затруднения;

Организация учебного процесса на этапе 4:

-Что в математике нам помогает выйти из затруднения?

(Наблюдение, рассуждения, анализ, схемы и рисунки)

— Правильно. Наблюдать, рассуждать и анализировать вы будете в группах, работая по плану над предложенными заданиями

5. Реализация плана выхода из затруднения.

1) организовать работу в группах по предложенному плану для построения нового способа действия, устраняющего причину выявленного затруднения;

2) зафиксировать новый способ действия в знаковой, вербальной форме и с помощью эталона.

Организация учебного процесса на этапе 4:

1 группа. (Способ сравнения с 1)

Задание: сравнить дроби:

Разбейте данное множество дробей на две группы:

Источник