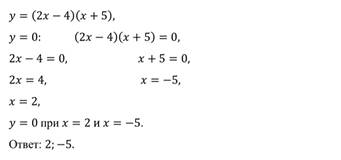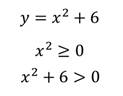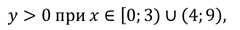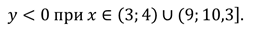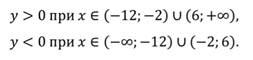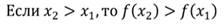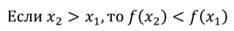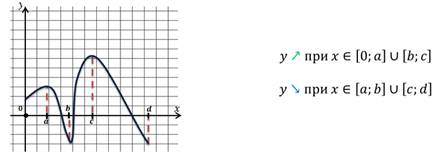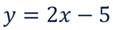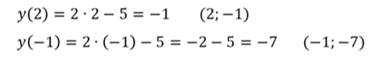Промежутки знакопостоянства что это
Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства.
теория по математике 📈 функции
Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.
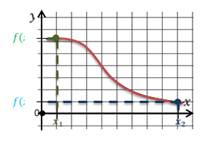
На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Остановимся подробнее на свойствах функций.
Нули функции
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.

Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
Находим х, разделив 22 на 11: х=22:11
Таким образом, мы нашли нуль функции: х=2
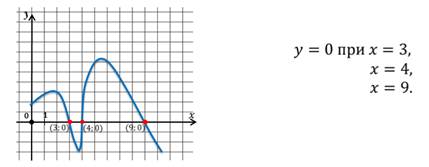
Пример №2. Найти нули функции у=f(x) по заданному графику.
Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.
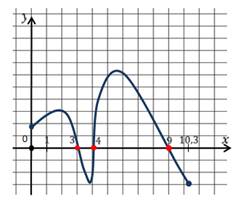
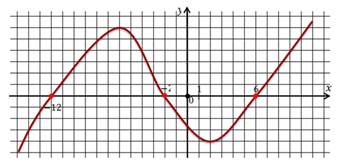
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
Возрастание и убывание функции
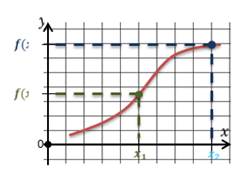
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.
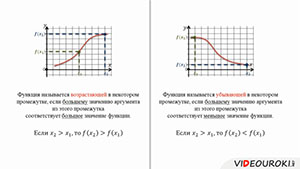
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Свойства функций
Урок 2. Алгебра 9 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Свойства функций»
На прошлом уроке мы с вами изучили понятие функция. Изучили её график и научились находить область определения и область значений функции.
· промежутки знакопостоянства функции;
· промежутки монотонности функции.
Нулями функции называют такие значения аргумента, при которых функция равна нулю.
В данном случае функция задана графически и мы определили нули функции по графику. Так же нули функции можно находить по формуле, с помощью которой задана функция.
Решив уравнение, мы найдём те значения х, при которых функция равна нулю.
Стоит обратить внимание на то, что не каждая функция имеет нули.
График не пересекает ось икс ни в одной точке.
Промежутки знакопостоянства функции
Функция принимает положительные значения:
И отрицательные значения:
Запишите промежутки знакопостоянства функции:
Положительные и отрицательные значения функции:
Промежутки монотонности функции
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции.
Функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Промежутками монотонности называют такие промежутки из области определения, на которых функция либо возрастает, либо убывает.
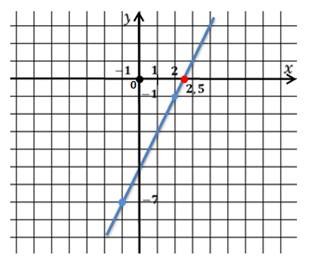
Опишем свойства функции:
Графиком является прямая, поэтому для построения достаточно двух точек:
Найдём значения функции:
Областью определения и областью значений будет множество всех действительных чисел. Ведь х и у могут быть любыми числами.
Как определить знаки постоянства функции
Подать заявку
Для учеников 1-11 классов и дошкольников

Итак, мы познакомились с функцией, узнали, что такое область определения и область значений функции. Теперь рассмотрим свойства функций. Их существует много, однако, изучаются они постепенно. В 9 классе мы знакомимся с нулями функции, промежутками возрастания и убывания (монотонность) и промежутками знакопостоянства и чётностью (нечётностью) функции. Рассмотрим их подробно.
Нулями функции называются значения независимой переменной (аргумента), при которых значение функции равно нулю. В графической интерпретации нулями функции являются абсциссы точек пересечения графика с осью абсцисс (осью х).
Промежутками знакопостоянства функции называются промежутки значений аргумента, на которых значения функции либо только положительны, либо только отрицательны. Другими словами, это те промежутки, на которых функция сохраняет свой знак.
Рассматривая график сверху, найдём промежутки знакопостоянства.
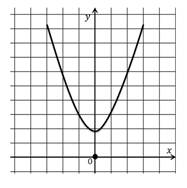
функция принимает только положительные значения на тех участках графика, где он находится выше оси Ох, т.е. при ;
Это неравенство можно решить двумя способами: с помощью систем неравенств и методом интервалов. Метод интервалов будет рассмотрен нами чуть позже, поэтому воспользуемся системами неравенств. Произведение двух множителей положительно, если эти множители имеют одинаковый знак. Значит, получается совокупность двух систем:
Теперь находим промежутки, на которых функция принимает отрицательные значения.
Произведение двух множителей отрицательно, если эти множители имеют разные знаки, т.е.
Чётной называется функция, если противоположным значениям аргумента соответствуют одинаковые значения функции, т.е. . График чётной функции симметричен относительно оси ординат (оси Оу).
Нечётной называется функция, если противоположным значениям аргумента соответствуют противоположные значения функции, т.е. . График нечётной функции симметричен относительно начала координат.
На рисунке слева график чётной функции, на рисунке справа – нечётной функции.
Для того, чтобы определить чётность функции, заданной аналитически, необходимо в заданную функцию вместо х подставить –х и произвести упрощение. Если в результате получится функция, равная заданной, то функция чётная; если получится функция, противоположная заданной, то она нечётная; если не получится ни один из предложенных вариантов, то функция не является ни чётной, ни нечётной.
Находим значение этой функции при противоположном значении х, т.е.
Полученное выражение не совпадает с заданным и не противоположно ему, значит, функция не является ни чётной, ни нечётной. Её график не симметричен относительно оси Оу и не симметричен относительно начала координат.
После упрощения получили выражение, полностью совпадающее с заданным. Значит, функция является чётной и её график симметричен относительно начала координат.
Функция называется возрастающей на некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции (или меньшему значению аргумента соответствует меньшее значение функции), т.е. если при , то функция возрастающая.
Функция называется убывающей на некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции (или меньшему значению аргумента соответствует большее значение функции), т.е. если при , то функция убывающая.
Для примера рассмотрим графики на рисунках выше.
Синий график: функция возрастает при
функция убывает при
Зелёный график: функция возрастает при
функция убывает при
Промежутки возрастания и убывания функции называются промежутками монотонности функции.
Если функция задана аналитически, то нахождение промежутков монотонности является более сложным процессом и он изучается в 11 классе. Мы ограничимся определением этих промежутков по графикам.
Наибольшим значением функции называется самое большое значение функции по сравнению со всеми остальными.
Наименьшим значением функции называется самое маленькое значение функции по сравнению со всеми остальными.
Строгое определение наибольшего и наименьшего значения функции будет дано в старших классах.
На зелёном графике нет ни наибольшего, ни наименьшего значения функции.
На рисунках изображены части графиков нечётных функций. Достройте эти графики.
Аналитический способ.
Аналитический способ — это наиболее часто встречающийся способ задания функции.
Заключается он в том, что функция задается формулой, устанавливающей, какие операции нужно произвести над х, чтобы найти у.
Графический способ.
При графическом способе вводится прямоугольная система координат и в этой системе координат изображается множество точек с координатами (x,y). При этом 
Словесный способ.
Функция задается с помощью словесной формулировки. Классический пример – функция Дирихле.
«Функция равна 1, если х – рациональное число; функция равна 0, если х – иррациональное число».
Табличный способ.
Табличный способ наиболее удобен, когда множество Х конечно. При этом способе составляется таблица, в которой каждому элементу из множества Х, ставится в соответствие число Y.
Типы ф-й
Сложная
Сложная функция — это функция от функции
Неявная
Неявные функции — это функции, заданные уравнением, не разрешенным относительно зависимой переменной.
Обратная
Если уравнение y=f(x) может быть однозначно разрешено относительного переменного x (т.е. сущ. Ф-я x=g(y) такая, что y=f[g(y)]), то ф-я x=g(y) – обратная по отношению к y=f(x).
Основные свойства функций.
1) Область определения функции и область значений функции.
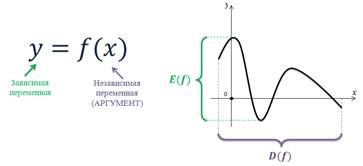
Область определения функции — это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена.
Область значений функции — это множество всех действительных значений y, которые принимает функция.
Нули функции.
Нуль функции – такое значение аргумента, при котором значение функции равно нулю.
Промежутки знакопостоянства функции.
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
Монотонность функции.
Возрастающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Четность (нечетность) функции.
Четная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.
Нечетная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = — f(x). График нечетной функции симметричен относительно начала координат.
Ограниченная и неограниченная функции.
Периодическость функции.
Функция f(x) — периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).
Предел ф-ии
Предел ф-ии (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.
Последовательность an называется бесконечно малой, если
Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.
Последовательность an называется бесконечно большой, если
Первый замечательный предел
Второй замечательный предел
Непрерывность ф-ии
Ф-яf(x) называется непрерывной при x = E, если
1) Эта ф-я определена в точке E, т.е. существует число f(E)
2) Существует конечный предел limf(x)
Точки разрыва
Точка х0 называется точкой разрыва функции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке.
Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.
Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
Производная сложной функции
Рассмотрим сложную функцию y = y(u(x))
Теорема 4. Если функции y = y(u), u = u(x) дифференцируемы (т.е. существуют производные y’u, u’x), тогда сложная функция y = y(u(x)) дифференцируема и y’x = y’u u’x.
Доказательство
Если аргумент x получит приращение Δx, то функция u получит приращение Δu = u(x + Δx) − u(x), а функция y получит приращение Δy = y(u + Δu) − y(u). Но тогда, воспользовавшись свойствами предела функции, получаем
Теорема доказана.
Доказательство
Если аргумент x получит приращение Δx, то функция f получит приращение Δy = f(x + Δx) − f(x). С другой стороны, для обратной функции g приращения Δx, Δy связаны следующим образом:Δx=g(y + Δy) − g(y).
Теорема доказана.
Производные высших порядков
Дифференцируемость функции
Функция y=f(x)называется дифференцируемой в некоторой точке x0, если она имеет в этой точке определенную производную, т.е. если предел отношения 
Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что онадифференцируема на отрезке [а; b] или соответственно в интервале (а; b).
Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.
Правило Лопиталя
Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть 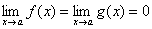
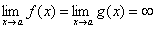
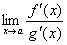
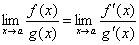 | (1) |
Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.
Замечание. Отметим, что формула (1) справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует.
Например, найти 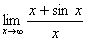
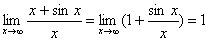
Заметим, что если отношение производных опять представляет собой неопределенность вида 0/0 или ∞/∞, то можно снова применить сформулированную теорему, то есть перейти к отношению вторых производных и так далее.
Вспомним, что к этим двум случаям сводятся случаи других неопределенностей: ∞·∞; 0·∞.
Для раскрытия неопределенностей 1∞, 10, ∞0 нужно прологарифмировать данную функцию и найти предел ее логарифма.
Монотонность ф-ии
Возрастающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Экстремумы
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках — ее экстремумами.
Первое достаточное условие.
Пусть xо — критическая точка. Если f ‘ (x) при переходе через точку xо меняет знак плюс на минус, то в точке xо функция имеет максимум, в противном случае — минимум. Если при переходе через критическую точку производная не меняет знак, то в точке xо экстремума нет.
Второе достаточное условие. Пусть функция f(x) имеет производную
f ‘ (x) в окрестности точки xо и вторую производную f»(xo) в самой точке xо. Если f ‘(xо) = 0, f»(xo)>0 (f»(xo) 0 при x > x0. Тогда при x x0 – вогнута. Следовательно, точка A, лежащая на кривой, с абсциссой x0 есть точка перегиба. Аналогично можно рассматривать второй случай, когда f »(x) > 0 при x x0.
Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует.
Асимптоты графика функции
Прямая называется асимптотой графика функции y = f(x), если расстояние от переменной точки M графика до этой прямой при удалении точки M в бесконечность стремится к нулю, т.е. точка графика функции при своем стремлении в бесконечность должна неограниченно приближаться к асимптоте.
Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от нее или с разных сторон, бесконечное множество раз пересекая асимптоту и переходя с одной ее стороны на другую.
Формула Тейлора
Формула Тейлора показывает поведение функции в окрестности некоторой точки. Формула Тейлора функции часто используется при доказательстве теорем в дифференциальном исчислении.
ФОРМУЛА ТЕЙЛОРА
, где Rn(x) — остаточный член формулы Тейлора.
Аналитический способ.
Аналитический способ — это наиболее часто встречающийся способ задания функции.
Заключается он в том, что функция задается формулой, устанавливающей, какие операции нужно произвести над х, чтобы найти у.
Графический способ.
При графическом способе вводится прямоугольная система координат и в этой системе координат изображается множество точек с координатами (x,y). При этом 
Словесный способ.
Функция задается с помощью словесной формулировки. Классический пример – функция Дирихле.
«Функция равна 1, если х – рациональное число; функция равна 0, если х – иррациональное число».
Табличный способ.
Табличный способ наиболее удобен, когда множество Х конечно. При этом способе составляется таблица, в которой каждому элементу из множества Х, ставится в соответствие число Y.
Типы ф-й
Сложная
Сложная функция — это функция от функции
Неявная
Неявные функции — это функции, заданные уравнением, не разрешенным относительно зависимой переменной.
Обратная
Если уравнение y=f(x) может быть однозначно разрешено относительного переменного x (т.е. сущ. Ф-я x=g(y) такая, что y=f[g(y)]), то ф-я x=g(y) – обратная по отношению к y=f(x).
Основные свойства функций.
1) Область определения функции и область значений функции.
Область определения функции — это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена.
Область значений функции — это множество всех действительных значений y, которые принимает функция.
Нули функции.
Нуль функции – такое значение аргумента, при котором значение функции равно нулю.
Промежутки знакопостоянства функции.
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
Монотонность функции.
Возрастающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.
Ответ или решение 1
Решение: Интервал знакопостоянства – это интервал, в каждой точке которого функция положительна либо отрицательна.
Существует следующий алгоритм метода интервалов :
Теперь выполняем задание в указанном порядке:
областью определения этой функции будут промежутки:
В нашем случае: x / (9 — x 2 ) = 0; очевидно что x = 0
3) Откладываем все найденные точки на числовой оси OX точки:
Определяем знак функции на интервалах.
Чтобы выяснить знак функции на каком-либо интервале, достаточно подставить в функцию любое число из этого интервала.
Из (0 ; 3) выбери число 1;
Из ( 3 ; ∞) выбери число 4;
Ответ: Промежутки знакопостоянства :