Произведение противоположных чисел чему равно

Противоположные числа, определение, примеры

В рамках этой статьи мы попробуем разобраться, что же такое противоположные числа. Мы поясним, что вообще они из себя представляют, покажем, какие именно обозначения используют для них, и разберем несколько примеров. В последней части материала мы перечислим основные свойства противоположных чисел.

Что такое противоположные числа

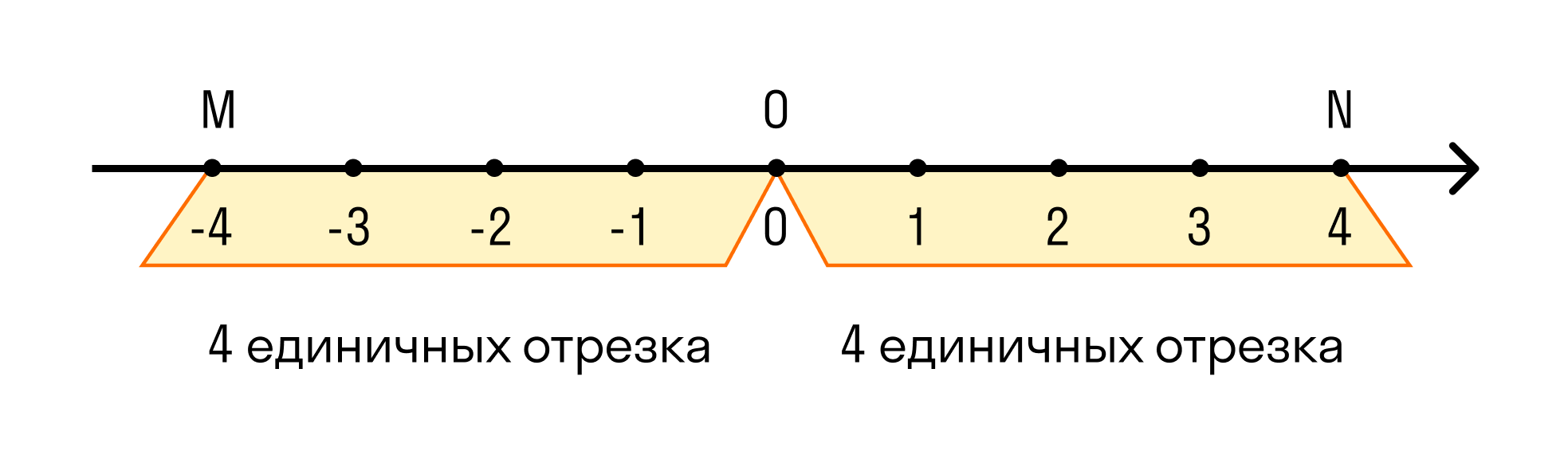
Вспомним, что каждой точке на координатной прямой можно поставить в соответствие только одно действительное число. В таком случае нашим точкам M и N соответствуют определенные числа, которые и называются противоположными. Каждое число имеет противоположное число, за исключением нуля. Поскольку это начало отсчета, то его считают противоположным самому себе.

Запишем определение, что же такое противоположные числа:

Противоположными называются числа, которым соответствуют такие точки на координатной прямой, в которые мы попадем, если отметим одно и то же расстояние от начала отсчета в разных направлениях (положительном и отрицательном). Нуль находится в начале отсчета и противоположен сам себе.

Как обозначаются противоположные числа

В этом пункте мы введем основные обозначения для таких чисел. Если у нас есть некое число и нам нужно записать противоположное ему, то для этого используем минус.

Основные свойства противоположных чисел

Таким числам присущи определенные свойства. Ниже мы дадим их список с пояснениями.

1. Если исходное число положительно, то противоположное ему будет отрицательно.

Это утверждение очевидно и следует из графика выше: такие числа находятся по разные стороны отсчета на координатной прямой. Если вы позабыли понятия положительных и отрицательных чисел, посмотрите материал, что мы публиковали раньше.

2. Следующее свойство принято называть свойством симметричности. Его также можно вывести из самого определения противоположных чисел. Оно звучит так:

Очевидно, что в дополнительных доказательствах это утверждение не нуждается.

3. Третье свойство противоположных чисел гласит:

Каждое действительное число имеет только одно противоположное число.

Это утверждение вытекает из того, что точкам координатной прямой не может соответствовать много чисел сразу.

4. Модули противоположных чисел равны.

Это следует из определения модуля. Логично, что точки на прямой, соответствующие любым противоположным числам, находятся на одном и то же расстоянии от точки отсчета.

Приведем примеры таких вычислений:

Как видно, это правило работает для всех чисел – целых, рациональных, иррациональных и др.

Источник

Противоположные числа

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Определение противоположных чисел

В 6 классе каждый школьник должен узнать, какие числа являются противоположными. Сейчас расскажем! Для начала построим координатную прямую.

Координатная ось — это прямая линия, на которой отмечено начало координат, задан масштаб и стрелкой указано положительное направление.

Противоположными называются числа, которым соответствуют такие точки на координатной прямой, в которые мы попадем, если отметим одно и то же расстояние от начала отсчета в разных направлениях (положительном и отрицательном). Нуль при этом находится в начале отсчета и противоположен сам себе.

Пары противоположных чисел:

Целые числа включают в себя натуральные числа, числа противоположные натуральным (то есть с отрицательным знаком) и ноль.

Обозначение противоположных чисел

У противоположных чисел есть основные обозначения. Если нам дано число и нужно записать противоположное ему, то для этого нужно использовать знак минус: «-».

Противоположные числа — это два числа, которые отличаются друг от друга знаками.

Примеры противоположных чисел:

Примеры противоположных рациональных чисел:

Свойства противоположных чисел

Перечислим основные свойства противоположных чисел:

Это объясняется тем, что для каждой точки координатной оси существует только одна точка, симметричная ей относительно нуля.

Это свойство следует из того, что противоположные числа находятся на координатной оси по разные стороны от нуля и имеют разные знаки. Исключение: число нуль (0).

Значит, если исходное число со знаком плюс, то противоположное ему будет со знаком минус. А если исходное число является отрицательным, то противоположное ему будет положительным.

Точки координатной прямой, которые соответствуют противоположным числам, находятся на одинаковом расстоянии от начала отсчета.

То есть, такие числа одинаковы по модулю, но имеют разные знаки.

Задания для самопроверки

Назовите число, противоположное данному:

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Источник

Модуль числа

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение модуля числа

Алгебра дает четкое определение модуля числа. Модуль в математике — это расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу.

Если мы возьмем некоторое число «a» и изобразим его на координатной прямой точкой A — расстояние от точки A до начала отсчёта (то есть до нуля) длина отрезка OA будет называться модулем числа «a».

Знак модуля: |a| = OA.

Разберем на примере:

Точка В, которая соответствует числу −3, находится на расстоянии 3 единичных отрезков от точки O (то есть от начала отсчёта). Значит, длина отрезка OB равна 3 единицам.

Число 3 (длину отрезка OB) называют модулем числа −3.

Обозначение модуля: |−3| = 3 (читают: «модуль числа минус три равен трём»).

Точка С, которая соответствует числу +4, находится на расстоянии четырех единичных отрезков от начала отсчёта, то есть длина отрезка OС равна четырем единицам.

Число 4 называют модулем числа +4 и обозначают так: |+4| = 4.

Также можно опустить плюс и записать значение, как |4| = 4.

Записывайся на занятия по математике для учеников с 1 по 11 классы.

Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Свойства модуля числа

Давайте рассмотрим семь основных свойств модуля. Независимо от того, в какой класс перешел ребенок — эти правила пригодятся всегда.

1. Модуль числа — это расстояние, а расстояние не может быть отрицательным. Поэтому и модуль числа не бывает отрицательным:

2. Модуль положительного числа равен самому числу.

3. Модуль отрицательного числа равен противоположному числу.

4. Модуль нуля равен нулю.

5. Противоположные числа имеют равные модули.

6. Модуль произведения равен произведению модулей этих чисел.

Геометрическая интерпретация модуля

Как мы уже знаем, модуль числа — это расстояние от нуля до данного числа. То есть расстояние от точки −5 до нуля равно 5.

Нарисуем числовую прямую и отобразим это на ней.

Эта геометрическая интерпретация используется для решения уравнений и неравенств с модулем. Давайте рассмотрим на примерах.

Решим уравнение: |х| = 5.

Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно 5. Это точки 5 и −5. Значит, уравнение имеет два решения: x = 5 и x = −5.

График функции

График функции равен y = |х|.

Для x > 0 имеем y = x.

Этот график можно использовать при решении уравнений и неравенств.

Корень из квадрата

Оно равно a при а > 0 и −а, при а

Модуль комплексного числа

Чему равен модуль числа в данном случае? Это арифметический квадратный корень из суммы квадратов действительной и мнимой части комплексного числа:

Свойства модуля комплексных чисел

Модуль рационального числа

Как найти модуль рационального числа — это расстояние от начала отсчёта до точки координатной прямой, которая соответствует этому числу.

Модуль рационального числа, примеры:

Модуль вещественных чисел

Модуль противоположного числа, нуля, отрицательного и положительного чисел

Закрепим свойства модуля числа, которые мы рассмотрели выше:

Источник

Противоположные числа

Всего получено оценок: 498.

Всего получено оценок: 498.

Тема «Противоположные числа» изучается в курсе 6 класса математики. У противоположных чисел есть ряд интересных свойств, которые выделяют их из множества действительных чисел. Рассмотрим основные понятия этой темы.

Определение противоположных чисел

Противоположными называются два числа, которые отличаются друг от друга только знаком.

Примеры

Приведем несколько примеров пар противоположных чисел:

Противоположные числа на координатной оси

Проведем координатную ось – прямую линию, на которой отмечено начало координат, задан масштаб и стрелкой указано положительное направление.

Рис. 1. Изображение противоположных чисел на координатной оси.

Из рис. 1 видно, что противоположные числа расположены на одинаковом расстоянии, но в противоположных направлениях от начала координатной оси. Поэтому такие числа и называются противоположными.

Как найти число, противоположное данному

Сформулируем правило, по которому мы можем написать два противоположных числа.

Пусть дано число a. Чтобы найти противоположное ему число, нужно к числу a приписать знак « – ».

Есть только одно число, которое является противоположным самому себе. Это число 0 (нуль).

В городе Будапеште, который является столицей Венгрии, установлен памятник нулю. Высота памятника составляет 3 м.

В России тоже есть несколько мест, которые называют памятниками нулю. Например, памятный знак нулевого километра у Воскресенских ворот в Москве.

Многие считают, что если кинуть монетку так, чтобы попасть на бронзовый памятный знак, и загадать желание, оно обязательно сбудется. А если это высокие памятники, как памятник в Будапеште, то существует следующая легенда: нужно пролезть внутрь нуля – тогда к зарплате прибавится несколько нулей.

Основные свойства противоположных чисел

Перечислим основные свойства противоположных чисел. Справедливость этих свойств подтверждает рис. 1.

Это объясняется тем, что для каждой точки координатной оси существует только одна точка, симметричная ей относительно нуля.

Это свойство следует из того, что противоположные числа находятся на координатной оси по разные стороны от нуля, они имеют разные знаки.

Исключение: число 0.

Таким образом, если исходное число является положительным, то противоположное ему будет отрицательным. А если исходное число является отрицательным, то противоположное ему будет положительным.

Это объясняется тем, что они одинаковы по модулю, но имеют разные знаки.

Пример

Рассмотрим число 4.

Найдем сумму этих чисел:

Что мы узнали?

Из темы по алгебре, которая изучается в 6 классе, мы узнали, что противоположные числа образуют пару чисел, из которых одно является положительным, а второе – отрицательным. Единственным исключением является число 0, которое противоположно самому себе. На числовой (координатной) оси противоположные числа находятся на одинаковых расстояниях, но в противоположных направлениях от начала координат.

Источник

Урок 28 Бесплатно Противоположные числа

Мир вокруг нас разнообразен и противоречив. В раннем детстве родители учили нас, что хорошо, а что плохо, читали нам сказки, где было добро и зло.

Очень часто в жизни мы используем противоположные понятия, может быть даже не замечая того.

Например, большой и маленький, высокий и низкий, правда и ложь, левый и правый, верх и низ и т.п.

Все перечисленные примеры, попарно имеют прямо противоположные лексические значения. В русском языке их называют антонимами.

Давайте разберёмся, что означает слово «противоположный».

Значение слова противоположный в толковом словаре Ожегова означает «расположенный напротив».

В различных науках можно встретить огромное множество противоположностей (противоположных понятий, явлений, процессов).

Является ли математика исключением? Конечно же, нет.

В математике существует не мало противоположностей: деление и умножение, четное число и нечетное число, больше и меньше, кривая и прямая, отрицательное число и положительное число.

Сегодня на уроке мы попробуем разобраться, какие числа называют противоположными, как обозначают противоположные числа, как изображают их на координатной прямой.

Выделим некоторые свойства и правила, характерные для противоположных чисел.

Противоположные числа

Вам уже известно, что положительными называют числа, которые обозначаются со знаком «+» или вообще без знака.

Отрицательными называют числа, которые обозначают со знаком «—».

У меня есть дополнительная информация к этой части урока!

Знаки сложения и вычитания были еще у древних египтян в виде иероглифов, похожих на ноги и направленных в разные стороны: при сложении в одну сторону, при вычитании в другую.

В начале ХV века в научных трудах европейских математиков в качестве знаков операции «плюс» и «минус» применяли латинские буквы «Р» и «М» соответственно.

В конце ХV века итальянский математик Лука Пачели вводит символы «\(\mathbf<\tilde

>\)» и «\(\mathbf<\tilde>\)».

В 1489 году немецкий математик Иоган Видман в своем научном трактате использует символ «+» и «—» (как minus и mer- от немецкого mehr означает «больше»).

Вместе с осознанием практической значимости отрицательных чисел встал вопрос о способе их обозначения.

В 1484 году Николя Шуке предложил перед отрицательными числами ставить знак, который в то время уже принимали в качестве знака операции вычитания «\(\mathbf<\tilde>\)».

В 1489 году были введены символы «+» и минус «—», похожие на современные символы.

Математики перед отрицательными числами стали применять минус, но часть ученых это не одобрило, указав на то, что не стоит вводить путаницу и использовать один и тот же знак для обозначения отрицательного числа и знака математической операции вычитания.

Не согласны они были еще и с тем, что знак отрицания числа можно было перепутать со знаком тире.

Предлагались различные замены знака отрицательного числа «—» на другие. Например, выдвигались идеи изображать в виде уголков или убывающей (возрастающей) луны.

Фаркаш Бойян предложил применять для обозначения знака числа все те же «+» и «—», но с другим начертанием.

Таким образом, использование знаков «+» и «—» как знаков числа и двойное обозначение минуса закрепилось в науке и действует по сегодняшний день.

Давайте разберемся на примере, какие числа называют противоположными.

Пример:

Две маленькие инерционные машинки запустили с одинаковой скоростью по одной прямой.

Обе машинки за равный промежуток времени откатились на 3 м по прямой, но первая машинка откатилась вправо от места запуска, а вторая машинка влево от места запуска.

Изобразим координатную прямую и отметим на ней координаты точек остановки этих двух машинок.

Вправо откладываем координату первой машинки А (+3)

Влево откладываем координату второй машинки А₁ (-3)

Мы можем заметить, что обе машинки проехали равный путь, так как координаты А (+3) и А₁ (-3) удалены от точки отсчета на одинаковые расстояния, но по разные стороны от точки О.

Два числа называются противоположными, если соответствующие им точки на координатной прямой расположены по разные стороны от точки начала отсчета и на одинаковом расстоянии от нее.

Таким образом, можно сказать, что:

Два числа, отличные друг от друга только знаками, называются противоположными числами.

Как вы успели заметить, чтобы обозначить число, противоположное данному, нужно это число записать со знаком минус «-».

+3,5 и -3,5 являются противоположными

-2 и 2 являются противоположными

-0,5 и 0,5 являются противоположными

-2 и +5 не являются противоположными (так как числа различны не только по знаку, но и по числовому значению).

6,3 и -6 не являются противоположными (так как числа различны не только по знаку, но и по числовому значению).

Пройти тест и получить оценку можно после входа или регистрации

Свойства и правила, характерные для противоположных чисел

Таким образом, знак минус «—» показывает противоположность числа.

-(-а) = а

Первый минус, читая запись, заменяют словами «Число, противоположное числу -а…».

-(-b) = b

-(-6,1) = 6,1

-(-4/5) = 4/5

2. Число ноль противоположно самому себе.

3. Для каждого действительного числа есть единственное противоположное число.

Так как для конкретной точки координатной прямой соответствует единственное действительное число.

4. Противоположные числа имеют свойство симметричности, то есть если число а противоположно числу b, то и число b противоположно числу а.

-7 противоположно числу 7

И верно, что 7 противоположно -7

5. Числа, которые используют для счета предметов, называют натуральными числами, множество натуральных чисел обозначают N =

Для чисел противоположных натуральным не стали придумывать определенного названия, но если рассматривать в совокупности все натуральные числа и все противоположные натуральным числа и ноль, то такие числа называют целые числа.

Множество целых чисел обозначается: Z =

У меня есть дополнительная информация к этой части урока!

Наглядным примером применения противоположных чисел в жизни является термометр жидкостный (спиртовой), который используется в метрологии.

Подобный термометр возможно применять при высоких и низких температурах, так как рабочим веществом в нем является этиловый спирт (температура замерзания ниже -100\(^\circ\)C).

Подобно вертикальной координатной прямой, на термометр нанесена шкала с делениями.

Задан единичный отрезок (цена деления прибора) и точка отсчета.

За точку отсчета по шкале Цельсия (шкала названа в честь шведского ученого Андерса Цельсия) выбрана температура замерзания воды- это 0\(^\circ\)C.

Все, что ниже, обозначаются отрицательными значениями (низкие температуры).

Отметка 20\(^\circ\)C будет располагаться выше точки отсчета 0\(^\circ\)C, т.к. это положительное температурное значение, означает 20\(^\circ\)C тепла.

А мы знаем, что два числа называются противоположными, если соответствующие им точки на координатной прямой расположены по разные стороны от точки начала отсчета и на одинаковом расстоянии от нее, значит:

Пройти тест и получить оценку можно после входа или регистрации

Источник