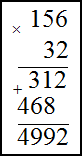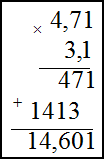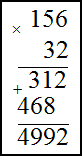Произведение чисел что это за действие
Произведение чисел что это за действие
Что такое произведение чисел (онлайн калькулятор на умножение)
Одна из важных математических операций это произведение чисел. Что же скрыто за этими словами как произведение, умножение. Именно об этом в нашей статье.
Давайте наверное начнем с банальных вещей. Когда у нас появляется много чего-то, то довольно сложно это хранить даже в виде информации. Нам каким-то образом это приходится компактно сокращать. Вот скажем у нас появилось более чем две пары носков в шкафу, а точнее пусть их будет 15. Как нам из записать на бумаге. Да, конечно, мы можем взять и записать 2+2+2. и так далее, пока не перечислим цифру два, с которой ассоциируется одна из пар носков на их количество, то есть на 15. Но это ведь право не удобно, особенно если представить, что речь идет не только о наших носках в шкафу, но и о случае их хранения в магазине! И здесь проще записать словами так. У нас две пары носков взято какое-то количество раз!
Вот, здесь где-то и образуется эта самая магия перехода от обычной суммы к произведению, когда мы подразумеваем, что берем какое-то число какое-то количество раз. Самое время дать определение.
Определение произведения чисел
Произведение двух чисел это есть не что иное, как взятое одно из чисел в количестве другого числа.
Еще раз! Если произведение будет С, то номинальное значение одного из чисел пусть а, взятое в количестве b раз и будет этим произведением. Можно записать скажем так
С=а1+а2+а3+а4. +аb где 1,2,3,4. b будут индексом указывающим на то, какое это число а по порядку и не более того!
Пример Найти произведение чисел:
Свойства произведения чисел
Коммутативность: n⋅m=m⋅n
Ассоциативность: (n⋅m)⋅k=n⋅(m⋅k)
На основании этих свойств можем заключить, что при перестановке множителей значение произведения не меняется.
Пример Найти произведение чисел удобным способом:
Решение. По свойства умножения имеем:
Если устное умножение чисел затруднительно используют умножение в столбик. В столбик можно умножать большие натуральные числа или десятичные дроби.
Пример Найти произведение чисел
Решение. Запишем умножаемые числа в столбик. Далее умножим сначала единицы второго числа на первое, полученное произведение запишем под чертой. Затем аналогично умножим десятки второго числа на первое. Результат запишем под первым произведением только на один разряд левее. В конце найдем сумму полученных произведений по правилу сложения в столбик
Побалуемся с произведением!?
Цифра которую будем брать N раз (множитель)
А чему равно это самое N раз?(множитель)
Числа. Произведение чисел. Свойства умножения.
Умножение — одно из четырёх основных арифметических действий, бинарная математическая операция, в которой один аргумент складывается столько раз, сколько показывает другой.
Произведение чисел m и n — это сумма n слагаемых, каждое из этих слагаемых = m.
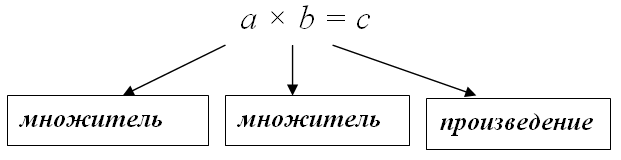
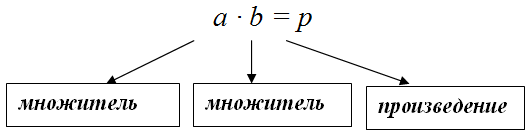
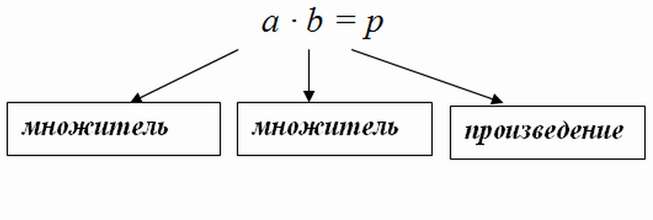
Выражение типа m • n, и значение такого выражения называется произведение чисел m и n. Числа m и n называются множителями.
Если устное умножение чисел затруднительно используют умножение в столбик. В столбик можно умножать большие натуральные числа или десятичные дроби.
Свойства умножения чисел.
1. Коммутативность: 
При перестановке множителей местами, значение произведения остается без изменений. Это переместительное свойство умножения.
где, 3 и 4 — множители, а 12 — произведение.
2. Ассоциативность: 
В произведении 3-х и больше множителей при перестановке этих множителей либо изменения последовательности выполнения умножения результат остается одинаковым.
3. Дистрибутивность: 
4. Произведение всякого натурального числа и единицы, будет соответствовать этому числу.
Произведение всякого натурального числа и нуля, = 0.
Выражения с буквенными множителями записывают так:
Кроме того, не используют знак умножения и перед скобками,
2 • (a + b) записывают как 2(а + b),
Умножение или произведение натуральных чисел, их свойства.
Умножение натурального числа.
Разберем понятие умножение на примере:
Туристы находились в пути три дня. Каждый день они проходили одинаковый путь по 4200 м. Какое расстояние они прошли за три дня? Решите задачу двумя способами.
Решение:
Рассмотрим задачу подробно.
В первый день туристы прошли 4200м. Во-второй день тот же самый путь прошли туристы 4200м и в третий день – 4200м. Запишем математическим языком:
4200+4200+4200=12600м.
Мы видим закономерность число 4200 повторяется три раза, следовательно, можно сумму заменить умножением:
4200⋅3=12600м.
Ответ: туристы за три дня прошли 12600 метров.
Рассмотрим пример: 
Чтобы нам не писать длинную запись можно записать ее в виде умножения. Число 2 повторяется 11 раз поэтому пример с умножением будет выглядеть так:
2⋅11=22
Подведем итог. Что такое умножение?
Умножение – это действие заменяющее повторение n раз слагаемого m.
Запись m⋅n и результат этого выражения называют произведением чисел, а числа m и n называют множителями.
Рассмотрим сказанное на примере:
7⋅12=84
Выражение 7⋅12 и результат 84 называются произведением чисел.
Числа 7 и 12 называются множителями.
В математике есть несколько законов умножения. Рассмотрим их:
Переместительный закон умножения.
Мы отдали по два яблока 5 своим друзьям. Математически запись будет выглядеть так: 2⋅5.
Или мы отдали по 5 яблок двум своим друзьям. Математически запись будет выглядеть так: 5⋅2.
В первом и втором случаем мы раздадим одинаковое количество яблок равное 10 штукам.
Если мы умножим 2⋅5=10 и 5⋅2=10, то результат не поменяется.
Свойство переместительного закона умножения:
От перемены мест множителей произведение не меняется.
m⋅n=n⋅m
Сочетательный закон умножения.
Рассмотрим на примере:
(2⋅3)⋅4=6⋅4=24 или 2⋅(3⋅4)=2⋅12=24 получим,
(2⋅3)⋅4=2⋅(3⋅4)
(a⋅b) ⋅c=a⋅(b⋅c)
Свойство сочетательного закона умножения:
Чтобы число умножить на произведение двух чисел, можно его сначала умножить на первый множитель, а затем полученное произведение умножить на второй.
Меняя несколько множителей местами и заключая их в скобки, результат или произведение не изменится.
Эти законы верны для любых натуральных чисел.
Умножение любого натурального числа на единицу.
Рассмотрим пример:
7⋅1=7 или 1⋅7=7
a⋅1=a или 1⋅a=a
При умножении любого натурального числа на единицу произведением будет всегда тоже число.
Умножение любого натурального числа на нуль.
6⋅0=0 или 0⋅6=0
a⋅0=0 или 0⋅a=0
При умножении любого натурального числа на нуль произведение будет равно нулю.
Вопросы к теме “Умножение”:
Что такое произведение чисел?
Ответ: произведением чисел или умножение чисел называется выражение m⋅n, где m – слагаемое, а n – число повторений этого слагаемого.
Для чего нужно умножение?
Ответ: чтобы не писать длинное сложение чисел, а писать сокращенно. Например, 3+3+3+3+3+3=3⋅6=18
Что является результатом умножения?
Ответ: значение произведения.
Что означает запись умножения 3⋅5?
Ответ: 3⋅5=5+5+5=3+3+3+3+3=15
Если умножить миллион на нуль, чему будет равно произведение?
Ответ: 0
Пример №1:
Замените сумму произведением: а) 12+12+12+12+12 б)3+3+3+3+3+3+3+3+3
Ответ: а)12⋅5=60 б) 3⋅9=27
Пример №2:
Запишите в виде произведения: а) а+а+а+а б) с+с+с+с+с+с+с
Решение:
а)а+а+а+а=4⋅а
б) с+с+с+с+с+с+с=7⋅с
Задача №1:
Мама купила 3 коробки конфет. В каждой коробке по 8 конфет. Сколько конфет купила мама?
Решение:
В одной коробке 8 конфет, а у нас таких коробок 3 штуки.
8+8+8=8⋅3=24 конфеты
Ответ: 24 конфеты.
Задача №2:
Учительница рисования сказала приготовить своим восемью ученикам по семь карандашей на урок. Сколько всего карандашей вместе было у детей?
Решение:
Можно посчитать суммой задачу. У первого ученика было 7 карандашей, у второго ученика было 7 карандашей и т.д.
7+7+7+7+7+7+7+7=56
Запись получилась неудобная и длинная, заменим сумму на произведение.
7⋅8=56
Ответ 56 карандашей.
Что такое произведение чисел
Определение произведения чисел
Задание. Найти произведение чисел:
1) 1.2$\cdot 3$ ; 2) 4$\cdot 5 \cdot 13$
Ответ.
$4 \cdot 5 \cdot 13=260$
Свойства произведения чисел
На основании этих свойств можем заключить, что при перестановке множителей значение произведения не меняется.
Что такое произведение чисел не по зубам? Тебе ответит эксперт через 10 минут!
Задание. Найти произведение чисел удобным способом:
1) 5$\cdot 17 \cdot 2$ ; 2) 7$\cdot 2 \cdot 15 \cdot 5$
Решение. По свойства умножения имеем:
$$5 \cdot 17 \cdot 2=(5 \cdot 2) \cdot 17=10 \cdot 17=170$$
$$7 \cdot 2 \cdot 15 \cdot 5=(7 \cdot(2 \cdot 15)) \cdot 5=(7 \cdot 30) \cdot 5=210 \cdot 5=1050$$
Ответ.
$5 \cdot 17 \cdot 2=170$
$7 \cdot 2 \cdot 15 \cdot 5=1050$
Если устное умножение чисел затруднительно используют умножение в столбик. В столбик можно умножать большие натуральные числа или десятичные дроби.
Задание. Найти произведение чисел
Решение. Запишем умножаемые числа в столбик. Далее умножим сначала единицы второго числа на первое, полученное произведение запишем под чертой. Затем аналогично умножим десятки второго числа на первое. Результат запишем под первым произведением только на один разряд левее. В конце найдем сумму полученных произведений по правилу сложения в столбик
Что такое произведение в математике?
Произведение – это умножение.
Так выражение вида a • b, а также значение этого выражения называют произведением чисел a и b. Числа a и b – это множители. Произведения как 3 • 4, так и 4 • 3 равны одному и тому же числу 12.
3 и 4 – множители, а 12 – произведение.
При перестановке множителей значение произведения не изменяется. Такое свойство выражения называют переместительным. Если его записать буквами, то оно будет выглядеть так:
Сочетательное свойство умножения выглядит так: a • (b • с) = (а • b) • c.
В произведении трёх и более множителей при их перестановке или изменении порядка выполнения умножения результат не изменяется.
Пример:
(4 • 2) • 3 = 8 • 3 = 24 или 4 • (2 • 3) = 4 • 6 = 24
Произведение любого натурального числа и единицы равно самому этому числу.
Произведение любого натурального числа и нуля, равно нулю.
Произведения с буквенными множителями записываются следующим образом:
вместо 6 • x пишут 6x, вместо a • b пишут ab
Также опускают знак умножения и перед скобками,
вместо 4 • (a + b) пишут 4(а + b),
вместо (x + 2) • (y + 3) пишут (x + 2)(y + 3),
вместо a • (b • c) пишут abc.
Вместе со статьёй «Что такое произведение в математике?» читают: