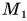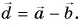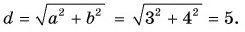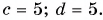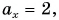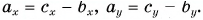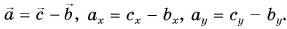Проекция что это такое в физике
Проекция что это такое в физике
1. Какая величина называется векторной (или просто вектором)?
Физическая величина, которая характеризуется не только числовым значением (модулем), но и направлением, называется векторной величиной (или просто вектором).
Для векторной величины одинаково важны числовое значение (модуль) и направление.
Примеры векторных величин:
— скорость,
— перемещение,
— сила.
2. Какая величина называются скалярной (или просто скаляром)?
Величины, которые не имеют направления и задаются только числом, называются скалярными величинами или скалярами.
Примеры скалярных величин:
3. Как изображают векторную величину?
Векторную величину изображают в виде стрелки, которая начинается в некоторой точке и заканчивается острием, указывающим направление..
Такой отрезок-стрелка называется вектором.
Длина стрелки в выбранном масштабе выражает модуль векторной величины.
Векторы обозначают буквами со стрелкой над ними.
Такой же буквой, но без стрелки обозначают модуль вектора.
4. Если два вектора равны друг другу по модулю, но направления векторов различны, то можно ли сказать, что эти векторы равны друг другу?
Нет, нельзя.
Равными считаются векторы, у которых одинаковы и модули, и направления.
5. Чем отличается векториая величина от скалярной?
Проекция вектора на координатную ось
1. Как построить проекцию вектора на координатную ось?

Есть вектор а.
Опустим из точки А (начало вектора) и точки В (конец вектора) перпендикуляры на ось ОX.
Получим на оси точки ха и хв — это проекции точек А и В на ось ОX.
Длину отрезка ха-хв между проекциями начала и конца вектора называют проекцией вектора а на ось ОX и обозначают, как ах.
Проекцию вектора на ось обозначают той же буквой, что и вектор, но без стрелки и с индексом оси.
Проекция вектора — величина скалярная.
2. Если вектор перемещения параллелен координатной оси, то чему равен модуль проекции вектора на эту ось?
Если вектор параллелен оси координат, то модуль его проекции ( |ax| ) равен модулю ( a ) самого вектора.
3. Что называют проекцией вектора на координатную ось?
Длину отрезка на координатной оси между проекциями начала и конца вектора, взятую со знаком « + » или « —», называют проекцией вектора а на координатную ось.
Проекция вектора на координатную ось может быть, как положительной, так и отрицательной.
Проекция вектора на ось считается положительной, если вектор сонаправлен с этой осью.
Проекция вектора на ось считается отрицательной, если вектор направлен противоположно оси.
Если вектор перпендикулярен координатной оси, то при любом направлении вектора его проекция на ось равна нулю.
Содержание:
Проекция вектора на ось:
Вы уже знаете, что вектор имеет модуль и направление. При решении задач часто используется понятие проекция вектора на ось. Что такое проекция вектора? Как ее определяют?
Начнем с понятия проекция точки на ось.
Проекция точки — это основание перпендикуляра, опущенного из данной точки на ось.
На рисунке 24 точка
Как определяют проекцию вектора на ось
Проекция вектора на ось — это длина отрезка между проекциями начала и конца вектора, взятая со знаком «+» или «-». Знак «+» берут, если угол между вектором и осью острый, а знак «-» — если угол тупой.
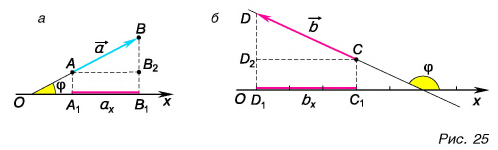
На рисунке 25 проекция вектора 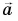
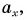
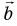
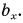
Проекция 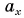
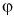
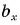
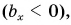
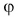
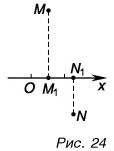
А если вектор перпендикулярен оси? Тогда его проекция на эту ось равна нулю (рис. 26).
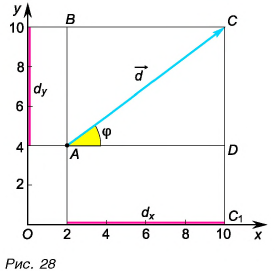
Проекцию вектора можно выразить через его модуль и угол между вектором и осью.
Рассмотрим треугольник 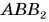
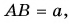
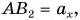
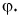
Проекция вектора на ось равна модулю вектора, умноженному на косинус угла между вектором и осью.
Это правило справедливо при любых углах между вектором и осью. Подтвердите это с помощью рисунков 25 и 26.
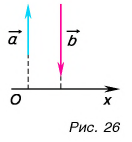
Обратим внимание на еще одно важное свойство проекций: проекция суммы векторов на ось равна сумме их проекций на эту ось.
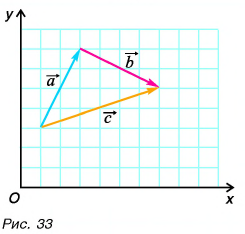
С помощью рисунка 27, а, б убедитесь, что из векторного равенства 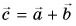
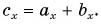
Можно ли найти модуль и направление вектора по его проекциям на координатные оси
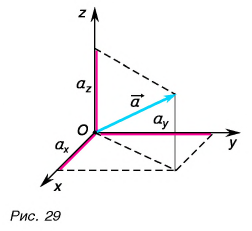
Рассмотрим вектор 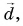
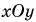
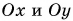
Модуль вектора 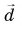
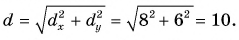
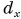
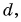
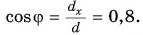
Таким образом, вектор, лежащий в заданной плоскости, полностью определяется двумя проекциями на оси координат.
Вектор в пространстве определяется тремя проекциями: 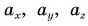
Главные выводы:
Пример №1
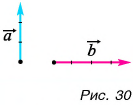
1. Определите сумму и разность взаимно перпендикулярных векторов 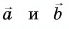
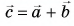
Решение
Сумму векторов 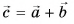
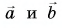
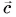
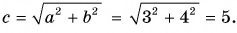
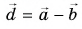
Модуль вектора 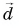
Ответ:
Пример №2
Выразите вектор 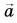
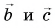
Решение
По правилу треугольника находим: 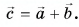
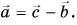
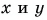
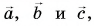
Вычислением убедимся, что проекции векторов связаны теми же равенствами, что и сами векторы:
Ответ:
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Проекция что это такое в физике
Учебник Физика 7 класс Кривченко И.В., размещённый в этой рубрике, включён в федеральный перечень учебников в соответствии с ФГОС. Учебник в цветном полиграфическом исполнении с твёрдым переплетом объёмом 150 страниц вышел из печати в июле 2015 г. в пятом издании. Учебник физики 7 класса рассчитан на 2 урока в неделю и содержит 6 тем курса физики, которые перечислены ниже.

Физика. Физическая величина. Измерение физических величин.
Цена делений шкалы прибора. Погрешность прямых и косвенных измерений.
Формулы и вычисления по ним. Единицы физических величин.
Метод построения графика.

Явление тяготения и масса тела. Свойство инертности и масса тела.
Плотность вещества. Таблицы плотностей некоторых веществ.
Средняя плотность тел и их плавание.
Метод научного познания.

Сила и динамометр. Виды сил.
Уравновешенные силы и равнодействующая.
Сила тяжести и вес тела. Сила упругости и сила трения.
Закон Архимеда. Вычисление силы Архимеда.
Простые механизмы. Правило равновесия рычага.

Определение давления. Давление жидкости. Закон Паскаля. Давление газа.
Атмосферное давление. Барометр Торричелли. Барометр-анероид.
Вакуумметры. Манометры: жидкостные и деформационные.
Пневматические и гидравлические механизмы.

Механическая работа. Коэффициент полезного действия. Мощность.
Энергия. Кинетическая и потенциальная энергия.
Механическая энергия. Внутренняя энергия.
Взаимные превращения энергии.

Температура и термометры. Количество теплоты и калориметр.
Теплота плавления/кристаллизации и парообразования/конденсации.
Первый закон термодинамики. Двигатель внутреннего сгорания.
Теплота сгорания топлива и КПД тепловых двигателей.
Теплообмен. Второй закон термодинамики.
 |
Учебник Физика 8 класс Кривченко И.В., размещённый в этой рубрике, включён в федеральный перечень учебников в соответствии с ФГОС. Учебник в цветном полиграфическом исполнении с твёрдым переплетом объёмом 150 стр. вышел из печати в июле 2015 г. в четвёртом издании. Учебник физики 8 класса рассчитан на 2 урока в неделю и содержит 5 тем курса физики, которые перечислены ниже.

Из истории МКТ. Частицы вещества. Движение частиц вещества.
Взаимодействие частиц вещества. Систематизирующая роль МКТ.
Кристаллические тела. Аморфные тела. Жидкие тела. Газообразные тела.
Агрегатные превращения. Насыщенный пар. Влажность воздуха.

Строение атомов и ионов. Электризация тел и заряд.
Объяснение электризации. Закон сохранения электрического заряда.
Электрическое поле. Электрический конденсатор. Электрический ток.
Электропроводность жидкостей, газов и полупроводников.

Электрическая цепь. Сила тока. Электрическое напряжение. Работа тока.
Закон Ома для участка цепи. Сопротивление соединений проводников.
Закон Джоуля-Ленца. Электронагревательные приборы.
Полупроводниковые приборы. Переменный ток.

Магнитное поле. Соленоид и электромагнит. Постоянные магниты.
Действие магнитного поля на ток. Электродвигатель на постоянном токе.
Электромагнитная индукция. Электротрансформатор. Передача электроэнергии.
Электродвигатель на переменном токе.

Период, частота и амплитуда колебаний. Нитяной и пружинный маятники.
Механические волны. Свойства механических волн. Звук.
Электромагнитные колебания. Излучение и прием электромагнитных волн.
Свойства электромагнитных волн. Принципы радиосвязи и телевидения.
 |
Учебник Физика 9 класс Кривченко И.В., размещённый в этой рубрике, включён в федеральный перечень учебников в соответствии с ФГОС. Учебник в цветном полиграфическом исполнении с твёрдым переплетом объёмом 150 стр. вышел из печати в июле 2015 г. в третьем издании. Учебник физики 9 класса рассчитан на 2 урока в неделю и содержит 4 темы курса физики, которые перечислены ниже.
Для перехода к параграфам кликайте нумерацию 01 02 03 04 05 и т.д. вверху страницы. Параграфы каждой темы курса физики снабжены интерактивными вопросами и заданиями.