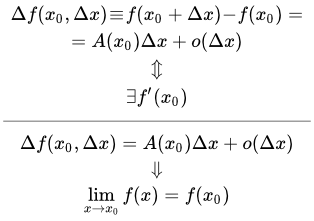Продифференцировать функцию это что значит
Правила дифференцирования: доказательство и примеры
Чтобы успешно решать задачи на дифференцирование, нужно уметь находить разные виды производных. Данная статья посвящена основным правилам дифференцирования, которые постоянно используются на практике. С помощью самого определения производной функции мы сформулируем доказательства всех этих правил и подробно рассмотрим несколько примеров, чтобы понять, как они применяются при решении задач.
Сформулируем основные проблемы дифференцирования:
Разберем все эти случаи по порядку.
Как вынести постоянный множитель за знак производной
Для начала нам нужно доказать следующую формулу:
Используя определение производной, запишем следующее:
Этим мы доказали первое правило дифференцирования. Разберем задачу на его применение.
Решение
Вынесем множитель за знак производной и получим:
Это самый простой пример. На практике чаще всего приходится предварительно преобразовывать дифференцируемую функцию, чтобы увидеть нужное значение в таблице производных и применить соответствующее правило.
Решение
Решение
Сначала нам нужно выполнить преобразование исходной функции.
Далее применяем изученное выше правило и берем из таблицы производных соответствующее значение:
Как вычислить производную суммы и производную разности
Так мы можем доказать равенство производной суммы или разности n-ного количества функций сумме или разности их производных:
Решение
Первым делом упрощаем данную функцию.
После этого применяем второе правило – производной суммы/разности:
Первое правило говорит нам о том, что можно вынести постоянный множитель за знак производной, значит:
Нам остается только заглянуть в таблицу производных и взять оттуда соответствующее значение:
Как вычислить производную произведения функций
Правило дифференцирования произведения двух функций выглядит следующим образом: f x · g ( x ) ‘ = f ‘ ( x ) · g ( x ) ‘ + f ( x ) · g ‘ ( x )
Попробуем доказать его.
Это и есть результат, который нам нужно было доказать.
Решение
y ‘ = ( t g x · a r c sin x ) ‘ = ( t g x ) ‘ · a r c sin x + t g x · ( a r c sin x ) ‘
Берем нужное значение из таблицы производных основных элементарных функций и записываем ответ:
Решение
Теперь разберем, что нужно делать в случае, когда производную нужно найти для произведения трех функций. По той же схеме решаются задачи с произведениями четырех, пяти и большего количества функций.
Решение
У нас получится следующее:
y ‘ = ( ( 1 + x ) · sin x · ln x ) ‘ = 1 + x · sin x ‘ · ln x + 1 + x · sin x · ln x ‘
1 + x · sin x ‘ = ( 1 + x ) ‘ · sin x + 1 + x · ( sin x ) ‘
С помощью этого правила и таблицы производных получим:
Теперь подставим в формулу то, что у нас получилось:
y ‘ = 1 + x · sin x · ln x ‘ = 1 + x · sin x ‘ · ln x + ( 1 + x ) · sin x · ( ln x ) ‘ = = sin x + cos x + x · cos x · ln x + ( 1 + x ) · sin x x
Ответ: y ‘ = sin x + cos x + x · cos x · ln x + ( 1 + x ) · sin x x
Из этого примера видно, что иногда приходится применять несколько правил дифференцирования подряд для вычисления нужного результата. Это не так сложно, как кажется, главное – соблюдать нужную последовательность действий.
Решение
Как вычислить производную частного двух функций (дробного выражения с функциями)
Сразу отметим, что g ( x ) не будет обращаться в 0 ни при каких значениях x из указанного промежутка. Согласно определению производной, получим:
Решение
После этого нам потребуется правило для суммы, а также правило вынесения постоянного множителя за знак производной:
Возьмем задачу на применение всех изученных правил.
Решение
Поясним, как это получилось.
Вычисляем третье слагаемое:
Теперь собираем все, что у нас получилось:
В задачах, которые мы разобрали в этой статье, использовались только основные элементарные функции, которые были связаны между собой знаками простых арифметических действий. Они нагляднее всего иллюстрируют правила дифференцирования. Однако возможно их применение и к более сложным функциям.
После того, как мы разберем, что такое производная сложной функции, мы сможете проводить дифференцирование выражений любой сложности.
Дифференцируемые функции в точке – определение и свойства
Определение дифференцируемой функции
Как мы увидим ниже, определение дифференцируемой функции одной переменной эквивалентно существованию ее производной. Тогда возникает вопрос – почему нельзя сразу дать определение, что дифференцируемая функция – это функция, имеющая производную?
Ответ на этот вопрос раскрывается при рассмотрении функций нескольких переменных. Дело в том, что производные вычисляются только от функций, зависящих от одной переменной. Для функций двух и более переменных, вначале выбирают направление приближения к заданной точке (например, ось x или ось y ), а затем по этому направлению вычисляют производную. Поэтому в любой точке имеется бесконечное множество производных по различным направлением. Из-за этого производные не фигурируют в определении дифференцируемой функции.
Свойства дифференцируемой функции
Таким образом, в случае функции от одной переменной, дифференцируемость функции в точке эквивалентно существованию производной в этой точке. Забегая вперед укажем, что в случае функций многих переменных, для того чтобы функция была дифференцируемой в точке, необходимо, чтобы она имела в этой точке частные производные, и достаточно, чтобы она имела в этой точке непрерывные частные производные.
Доказательства теорем
Связь дифференцируемости функции с существованием производной
В нашем случае это означает, что
.
Отсюда
.
Связь дифференцируемости функции с ее непрерывностью
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Продифференцировать функцию это что значит
При дифференцировании различают функции по способу их задания: явные, неявные и параметрические.
Производной функции y = f ( x ) по переменной x в некоторой точке называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю, то есть
Производная характеризует скорость изменения функции в достаточно малой окрестности заданной точки.
Приведем таблицу производных основных элементарных функций (без доказательства), которые рассматриваются нами как функции простые и явно заданные.
Следствие. В точках разрыва функция производной не имеет
Существуют такие точки, в которых функция непрерывна, но не дифференцируема. Так, функция y =| x | в точке x =0 непрерывна, но производной не имеет, так как в этой точке к графику функции можно провести бесконечное множество касательных (рис. 3.6). Такие точки называются угловыми или точками излома функции. Данный случай показывает, что обратное утверждение к теореме 3.9 неверно.
Среди явных функций особое место занимают обратные функции, производная которых находится с помощью следующей теоремы.
Теорема 3.10. Если строго монотонная функция y = f ( x ) дифференцируема на некотором интервале Х, причем ее производная не обращается в нуль на Х, то обратная к ней функция x = φ ( y ) также дифференцируема на этом интервале, при этом:
По определению производной можно записать:
Среди явных функций выделяют класс сложных функций.
Теорема 3.11. Чтобы продифференцировать сложную функцию необходимо сначала продифференцировать внешнюю функцию по внутренней, считая внутреннюю функцию независимой переменной, затем продифференцировать внутреннюю функцию по независимому переменному и результаты дифференцирования перемножить, то есть
Решение. Согласно формуле (3.31) и с учетом табли 
где t – параметр. Производную такой функции несложно получить:
Пример 3.9. Найти производную функции 
Решение. Согласно формуле (3.32) и с учетом табличных формул (3.18), (3.19) имеем:
Помимо таблицы производных имеют место правила дифференцирования.
Теорема 3.12. Производная суммы двух дифференцируемых функций равна сумме производных этих функций:
Данная теорема может быть обобщена для произвольного конечного числа функций-слагаемых.
Решение. Согласно формулам (3.33) и (3.31) и с учетом табличных формул (3.17), (3.20), (3.23) имеем:
Теорема 3.13. Производная произведения двух дифференцируемых функций равна произведению производной первой функции-сомножителя на вторую функцию плюс произведение первой функции на производную второй функции–сомножителя, то есть
Решение. Согласно формуле (3.34) и с учетом табличных формул (3.22), (3.24) имеем:
Теорема 3.14. Производная частного двух функций равна дроби, у которой знаменатель есть квадрат знаменателя данной дроби, а числитель есть разность между произведением знаменателя на производную числителя и произведением числителя на производную знаменателя, то есть
Решение. Согласно формуле (3.35) и с учетом табличных формул (3.17), (3.29) имеем:
Решение. Согласно формуле (3.31) дифференцирования сложной функции и (3.34) производной произведения, с учетом табличных формул (3.17) и (3.18) имеем:
Дифференциалом функции y = f ( x ) в точке x называется главная часть приращения этой функции, равная произведению производной функции на приращение аргумента:
Формула (3.39) применяется для вычисления приближенных значений функций.
Дифференцирование функции, нахождение производной
Если вам нужно решить задачу, в рамках которой требуется вычислить производную какой-либо функции с одной переменной, советуем внимательно прочесть эту статью. Здесь приводятся общие положения теории дифференцирования, имеющие отношение к вычислению производной. Для этого могут быть использованы разные способы, ведь исходная функция может быть задана явно или неявно, в параметрическом виде, быть элементарной, основной или сложной, значит, в каждой ситуации бывает нужен свой подход.
Таблица дифференцирования функции
Мы собрали всю информацию, которую нужно знать для правильного дифференцирования функции, и представили ее в табличном виде:
Степенная фунция y = x p
y = a x a x ‘ = a x · ln a
В частности, при a = e имеем
log a x ‘ = 1 x · ln a
В частности, при a = e имеем
y = ln x ln x ‘ = 1 x
Производная сложной функции
( f ( g ( x ) ) ) ‘ = f ‘ ( g ( x ) ) · g ‘ ( x )
Производная неявно заданной функции
Производная обратной функции
Обратные тригонометрические функции
Производная параметрически заданной функции
y = f ( x ) y ‘ = y · ( ln ( f ( x ) ) ) ‘
Пояснения таблицы
Содержимое таблицы требует небольших пояснений. Например, в наиболее простом случае для дифференцирования нам пригодится определение производной, т.е. вычисление соответствующего предела. Это действие носит название непосредственного дифференцирования.
Если вам приходится работать с основной элементарной функцией, то следует использовать таблицу основных производных. В ней приводятся все готовые значения, доказанные на основании определения. Это очень удобно, и мы советуем вам держать такую таблицу под рукой.