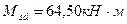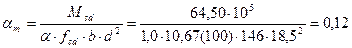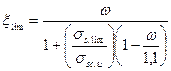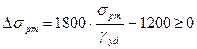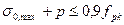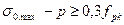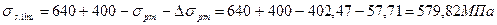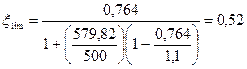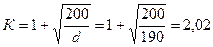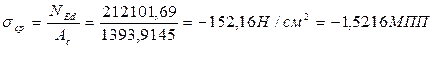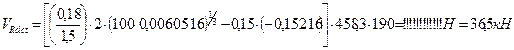Прочность по предельному моменту сечения что это значит

Прочность нормального сечения

Лекция 5

Расчет прочности нормальных сечений изгибаемых элементов

С одиночной арматурой

Условие прочности

Предельно воспринимаемый момент изгибаемого элемента любой симметричной формы с одиночной арматурой определяется из условия равновесия моментов внешних сил и внутренних усилий, относительно любой точки, рассматриваемого сечения.

Условие прочности нормального сечения

Положение нейтральной оси

Определяется из условия равенства нулю проекций всех сил на продольную ось элемента.

Отсюда находится высота сжатой зоны «х»

Граничная высота сжатой зоны

Под граничной высотой сжатой зоны x_R понимают такую высоту сжатого бетона, при которой происходит исчерпание несущей способности бетона сжатой зоны и растянутой арматуры одновременно (ξ_R=x_R/h₀).

Граничную высоту сжатой зоны определяют экспериментально. Для элементов без предварительного напряжения арматуры ξ_R находят по формуле

Для элементов с предварительным напряжением арматуры ξ_R определяется по формуле

ε_s,el – относительная деформация в растянутой арматуре при достижении в этой арматуре расчетного сопротивления:

• для арматуры с физическим пределом текучести

• для арматуры с условным пределом текучести

σ_sp— напряжения предварительного натяжения арматуры, принимается с учетом всех потерь при коэффициенте γ_sp= 0,9,

ε_b,2 – предельная о деформация сжатого бетона

Если соблюдается условие ξ = х / h₀ ≤ ξ_R расчетное сопротивление напрягаемой арматуры R_s допускается увеличивать путем умножения на коэффициент условий работы

Учитывая, что ξ = х/h₀, перепишем уравнение

Обозначим выражение ξ(1-0,5ξ) через α_m, тогда

Приравняв моменты М и М_сеч находим коэффициент

Прочность нормальных сечений элементов с одиночной арматурой

Оставляем только со знаком «-».

Из условия равенства прочности сечения по арматуре и бетону находится требуемое количество арматуры.

При значениях α_m > α_R требуется увеличить сечение или повысить класс бетона или установить сжатую арматуру. Если не поможет попытаться выполнить первую, вторую и третью рекомендации одновременно.

Практический расчет прочности нормальных сечений при ξ = х / h₀ ≤ ξ_R

Выполняется статический расчет и определяются усилия М, Q, N.

Вычисляется табличный коэффициент α_m.

Источник

Расчет прочности по нормальным и наклонным сечениям

Расчёт по нормальным сечениям производится по максимальному изгибающему моменту

Расчет выполняем с использованием таблиц, для чего вычисляем α_m по формуле:

При α_m=0,12 устанавливаем, что деформированное состояние соответствует области 1а, что означает достижение растянутой арматурой предельных деформаций. Вычисленному α_m=0,12 соответствует коэффициент 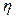= 0,930, ξ = 0,182

Высота сжатой зоны x= ξ∙d=0,21∙18,5=3,36 ’ _f=3,85 см, значит нейтральная ось действительно лежит в пределах полки толщиной h ’ _f.

Проверяем условие ξ ≤ ξ_lim, где 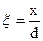— относительная высота сжатой зоны.

ξ_lim – граничные значения относительной высоты сжатой зоны сечения при которой предельное состояние элемента наступает одновременно с достижением в растянутой арматуре напряжением равного расчетному сопротивлению и определяется по формуле:

где ω – характеристика сжатой зоны бетона,

σ_sс.u – предельное напряжение в арматуре принимаемое 500 МПа.

где Δ σ_pm – напряжение от неупругих относительных деформаций напрягаемой арматуры.

Величина предварительного напряжения:

где 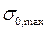— начальное контролируемое предварительное напряжение арматуры;

При электротермическом натяжении на упоры, что имеет место в данном случае p=30+360/l=30+360/7,04=81,14МПа,

где l – расстояние между наружными гранями упоров.

Тогда 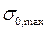=0,9f_pk-p=0,9∙800-81,14=638,86 МПа

Усилие в бетоне от предварительного напряжения на уровне центре тяжести арматуры:

= МПа

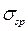
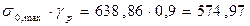
где γ_р=0,9 – частный коэффициент для усилия предварительного обжатия.

МПа

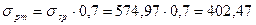
тогда Δσ_pm= 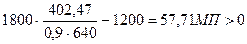, значит принимаем для расчета Δσ_pm=57,71 МПа

тогда

Расчет прочности по наклонному сечению производится по максимальной поперечной силе V_Sd=43,15 кН.

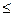
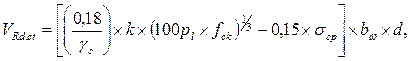
Расчёт прочности плиты на действие поперечных сил при отсутствии вертикальной арматуры согласно Норм проектирования следует производить из условия: V_Sd V_Rd.ct

но неменее

Принимаем 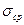=-1,5216 МПа

Тогда

Источник

Расчет на прочность: при растяжении, кручении и изгибе.

Автор: Константин Вавилов · Опубликовано 08.10.2016 · Обновлено 17.02.2018

Эта статья будет посвящена расчетам на прочность, которые выполняются в сопромате и не только. Расчеты на прочность бывают двух видов: проверочные и проектировочные (проектные).

Проверочные расчеты на прочность – это такие расчеты, в ходе которых проверятся прочность элемента заданной формы и размеров, под некоторой нагрузкой.

В ходе проектировочных расчетов на прочность определяются какие-то размеры элемента из условия прочности. Причем, очевидно, что для разных видов деформаций эти условия прочности различны. Также к проектным расчетам можно отнести расчеты на грузоподъемность, когда вычисляется максимальная нагрузка, которую может выдерживать конструкция, не разрушаясь. Рассмотрим более подробно, как проводится прочностные расчеты для разных случаев.

Расчеты на прочность при растяжении (сжатии)

Начнем, пожалуй, с самого простого вида деформации растяжения (сжатия). Напряжение при центральном растяжении (сжатии) можно получить, разделив продольную силу на площадь поперечного сечения, а условие прочности выглядит вот так:

где сигма в квадратных скобках – это допустимое напряжение. Которое можно получить, разделив предельное напряжения на коэффициент запаса прочности:

Причем, за предельное напряжение для разных материалов принимают разное значение. Для пластичных материалов, например, для малоуглеродистой стали (Ст2, Ст3) принимают предел текучести, а для хрупких (бетон, чугун) берут в качестве предельного напряжения – предел прочности (временное сопротивление). Эти характеристики получают при испытании образцов на растяжение или сжатие на специальных машинах, которые фиксируют характеристики в виде диаграммы.

Коэффициент запаса прочности выбирается конструктором исходя из своего личного опыта, назначения проектируемой детали и сферы применения. Обычно, он варьируется от 2 до 6.

В случае если необходимо подобрать размеры сечения, площадь выражают таким образом:

Таким образом, минимальная площадь поперечного сечения при центральном растяжении (сжатии) будет равна отношению продольно силы к допустимому напряжению.

Расчеты на прочность при кручении

При кручении расчеты на прочность в принципе схожи с теми, что проводятся при растяжении. Только здесь вместо нормальных напряжений появляются касательные напряжения.

На кручение работают, чаще всего, детали, которые называются валами. Их назначение заключается в передаче крутящего момента от одного элемента к другому. При этом вал по всей длине имеет круглое поперечное сечение. Условие прочности для круглого поперечного сечения можно записать так:

где Ip — полярный момент сопротивления, ρ — радиус круга. Причем по этой формуле можно определить касательное напряжение в любой точке сечения, варьируя значение ρ. Касательные напряжения распределены неравномерно по сечению, их максимальное значение находится в наиболее удаленных точках сечения:

Условие прочности, можно записать несколько проще, используя такую геометрическую характеристику как момент сопротивления:

То бишь максимальные касательные напряжения равны отношению крутящего момента к полярному моменту сопротивления и должны быть меньше либо равны допустимому напряжению. Геометрические характеристики для круга, упомянутые выше можно найти вот так:

Иногда в задачах встречаются и прямоугольные сечения, для которых момент сопротивления определяется несколько сложнее, но об этом я расскажу в другой статье.

Источник

Первое и второе предельное состояние при расчете конструкций

Что такое предельные состояния и как с ними разобраться применительно к расчетам конструкций? Все знают, что бывает две группы предельных состояний: первая и вторая. Что же обозначает это разделение?

Само название «предельное состояние» обозначает, что для любой конструкции при определенных условиях наступает такое состояние, при котором исчерпывается какой-то определенный предел. Условно, для удобства расчетов, таких пределов вывели два: первое предельное состояние – это когда исчерпывается предел прочности, устойчивости и выносливости конструкции; второе предельное состояние – когда деформации конструкции превышают предельно допустимые (ко второму предельному состоянию для железобетона также относят ограничение по возникновению и раскрытию трещин).

Перед тем, как перейти к разбору расчетов по первому и второму предельному состоянию, следует разобраться, какая часть расчета конструкции вообще делится на эти две части. Любой расчет начинается со сбора нагрузки. Затем следует выбор расчетной схемы и непосредственно расчет, в результате которого мы определяем усилия в конструкции: моменты, продольные и поперечные силы. И только после того, как усилия определены, мы переходим к расчетам по первому и второму предельному состоянию. Обычно они выполняются именно в такой последовательности: сначала по первому, потом по второму. Хотя бывают и исключения, но о них ниже.

Нельзя сказать, что для какой-то конструкции важнее: прочность или деформативность, устойчивость или трещиностойкость. Нужно проводить расчет по двум предельным состояниям и выяснять, какое из ограничений бывает наиболее неблагоприятным. Но для каждого типа конструкций есть свои особые моменты, которые полезно знать, чтобы было проще ориентироваться в среде предельных состояний. В этой статье мы на примерах разберем предельные состояния для различных типов железобетонных конструкций.

Расчет балок, плит и других изгибаемых элементов по первому и второму предельному состоянию

Итак, вам нужно рассчитать изгибаемый элемент, и вы думаете, с чего начать расчет, и как понять, все ли посчитано? Все рекомендуют сделать расчет не только по первому, но и по второму предельному состоянию. Но что же это такое? Где конкретика?

Для расчета изгибаемых элементов вам понадобится «Пособие по проектированию бетонных и железобетонных конструкций из тяжелых бетонов без предварительного напряжения арматуры (к СНиП 2.03.01-84)» и непосредственно сам СНиП 2.03.01-84 «Бетонные и железобетонные конструкции» обязательно с изменением 1 (очень важным для расчета по второй группе предельных состояний).

Открываете раздел 3 пособия «Расчет железобетонных элементов по предельным состояниям первой группы», а именно «Расчет железобетонных элементов по прочности» (начиная с п. 3.10). Теперь нужно выяснить, из каких этапов он состоит:

1) Расчет сечений, нормальных к продольной оси элемента – это та часть расчета, в которой мы проверяем, выдержит ли наша конструкция воздействие изгибающего момента. Проверяется сочетание двух важных факторов: размер сечения элемента и площадь продольной арматуры. Если проверка показывает, что действующий на конструкцию момент меньше предельно допустимого, значит все хорошо, и можно переходить к следующему этапу.

2) Расчет сечений, наклонных к продольной оси элемента – это расчет конструкции на действие поперечной силы. Для проверки нам важно установить размеры сечения элемента и площадь поперечной арматуры. Так же, как и на предыдущем этапе расчета, если действующая поперечная сила меньше предельно допустимой, прочность элемента считается обеспеченной.

Оба этапа вместе с примерами подробно рассмотрены в пособии. Эти два расчета являются исчерпывающими расчетами по прочности для классических изгибаемых элементов. Если есть какие-либо особые условия (многократно повторяющиеся нагрузки, динамика), их нужно учитывать в расчете на прочность и выносливость (зачастую, учет производится введением коэффициентов).

Далее открываем раздел 4 пособия «Расчет бетонных и железобетонных элементов по предельным состояниям второй группы». Рассмотрим этапы, из которых он состоит.

1) Расчет железобетонных элементов по образованию трещин – это самый первый этап, в котором мы выясняем, образуются ли трещины в нашем элементе при воздействии действующих на него усилий. Трещины не образуются, если наш максимальный момент Mr меньше момента Mcrc, вызывающего образование трещин.

2) Расчет железобетонных элементов по раскрытию трещин – это следующий этап, на котором мы проверяем величину раскрытия трещин в конструкции и сравниваем ее с допустимыми размерами. Обратите внимание на п. 4.5 пособия, в котором оговаривается, в каких случаях этот расчет выполнять не нужно – лишняя работа нам ни к чему. Если же расчет необходим, то нужно выполнить две его части:

б) расчет по раскрытию трещин, наклонных к продольной оси элемента – его нужно выполнять по п. 4.11 пособия, также с учетом изменения 1.

Естественно, если согласно первому этапу расчета трещины не образуются, то этап 2 мы пропускаем.

3) Определение прогиба – это последний этап расчета по второму предельному состоянию для изгибаемых железобетонных элементов, выполняется он согласно п. 4.22-4.24 пособия. В этом расчете нам нужно найти прогиб нашего элемента и сравнить его с прогибом, нормированным ДСТУ Б. В.1.2-3:2006 «Прогибы и перемещения».

Если все эти части расчетов выполнены, считайте, что расчет элемента как по первому, так и по второму предельному состоянию выполнен. Конечно, если есть какие-то особенности конструкции (подрезка на опоре, отверстия, сосредоточенные нагрузки и т.д.), то нужно дополнять расчет с учетом всех этих нюансов.

Расчет колонн и других центрально и внецентренно сжатых элементов по первому и второму предельному состоянию

Этапы этого расчета не особо отличаются от этапов расчета изгибаемых элементов, да и литература та же.

Расчет по предельному состоянию первой группы включает в себя:

1) Расчет сечений, нормальных к продольной оси элемента – этот расчет так же, как и для изгибаемых элементов, определяет необходимый размер сечения элемента и его продольное армирование. Но в отличие от расчета изгибаемых элементов, где проверяется прочность сечения на действие изгибающего момента М, в данном расчете выделяется максимальная вертикальная сила N и эксцентриситет приложения этой силы «е» (при перемножении, правда, они дают все тот же изгибающий момент). В пособии подробно изложена методика расчета для всех стандартных и нестандартных сечений (начиная с п. 3.50).

Особенностью данного расчета является то, что нужно учитывать влияние прогиба элемента, а также учитывается влияние косвенного армирования. Прогиб элемента определяется при расчете по второй группе предельных состояний, но допускается при расчете по первому предельному состоянию упростить расчет путем введения коэффициента согласно п. 3.54 пособия.

2) Расчет сечений, наклонных к продольной оси элемента – этот расчет на действие поперечной силы согласно п. 3.53 пособия аналогичен расчету изгибаемых элементов. В результате расчета мы получаем площадь поперечной арматуры в конструкции.

Расчет по предельному состоянию второй группы состоит из этапов:

1) Расчет железобетонных элементов по образованию трещин.

2) Расчет железобетонных элементов по раскрытию трещин.

Эти два этапа абсолютно аналогичны расчету изгибаемых элементов – имеются максимальные усилия, следует определить, образуются ли трещины; и если образуются, то сделать при необходимости расчет по раскрытию трещин, нормальных и наклонных к продольной оси элемента.

3) Определение прогиба. Точно так же, как и для изгибаемых элементов, нужно определять прогиб и для внецентренно сжатых элементов. Предельные прогибы как всегда можно найти в ДСТУ Б В.1.2-3:2006 «Прогибы и перемещения».

Расчет фундаментов по первому и второму предельному состоянию

Расчет фундаментов кардинально отличается от приведенных выше расчетов. Как всегда, при расчете фундаментов необходимо начать со сбора нагрузок либо с расчета каркаса здания, в результате которого определяться основные нагрузки на фундамент N, M, Q.

После того, как собраны нагрузки и выбран тип фундамента, необходимо перейти к расчету грунтового основания под фундаментом. Этот расчет, как и любые другие расчеты, делится на расчет по первому и по второму предельному состоянию:

1) обеспечение несущей способности основания фундамента – проверяется прочность и устойчивость оснований (первое предельное состояние) – пример расчета ленточного фундамента здесь;

2) расчет основания по деформациям – определение расчетного сопротивления грунта основания, определение осадки, определение крена фундамента (второе предельное состояние).

Разобраться с этим расчетом поможет «Пособие по проектированию оснований зданий и сооружений (к СНиП 2.02.01-83)».

Как вы уже поняли из формулировок, при определении размера подошвы фундамента (будь то лента или столбчатый фундамент), мы прежде всего выполняем расчет грунтового основания, а не фундамента. И в этом расчете (кроме скальных грунтов) намного важнее выполнить расчет основания по деформациям – все, что перечислено в пункте 2 выше. Расчет по первому предельному состоянию зачастую выполнять вообще не требуется, т.к. предотвратить деформации гораздо важнее, они возникают намного раньше, чем потеря грунтом несущей способности. В каких случаях следует выполнять расчет по первой группе предельных состояний, можно узнать из п. 2.259 пособия.

Теперь рассмотрим расчет основания по деформациям. Чаще всего проектировщики прикидывают расчетное сопротивление грунта, сравнивают его с нагрузкой на грунт от здания, подбирая необходимую площадь фундамента, и на этом останавливаются. Это неверный подход, т.к. выполнена лишь часть работы. Расчет фундамента считается завершенным, когда выполнены все этапы, перечисленные в пункте 2.

Очень важным является определение осадки фундаментов. Особенно это важно при различных нагрузках или неравномерных грунтах, когда есть риск возникновения неравномерных осадок фундаментов (подробно об этом изложено в этой статье «Что нужно знать о ленточном монолитном фундаменте»). Чтобы быть уверенным в дальнейшей целостности конструкций здания, всегда нужно проверять разность осадок фундаментов по таблице 72 пособия. Если разность осадок выше предельно допустимой, возникает риск возникновения трещин в конструкциях.

Крен фундамента необходимо определять при наличии изгибающих моментов, действующих на фундамент. Также крен нужно проверять при неравномерной нагрузке на грунте – она также влияет на деформации грунтового основания.

Но после того, как выполнен расчет основания по второму и возможно первому предельному состоянию и определены размеры подошвы фундамента, нужно перейти к следующему этапу: расчету самого фундамента.

Точно так же нужно действовать и в случае расчета ленточного фундамента: имея вылет подошвы в одну сторону от стены и давление под этой подошвой, мы рассчитываем консольную плиту (с защемлением на опоре), длина консоли равна вылету подошвы, ширина берется для удобства расчета равной одному метру, нагрузка на консоль равна давлению под подошвой фундамента. Находим максимальный момент и поперечную силу в консоли и выполняем расчет по первому и второму предельному состоянию – точно так, как описано в расчете изгибаемых элементов.

Таким образом, при расчете фундаментов мы проходим два случая расчета по предельным состояниям первой и второй группы: сначала при расчете основания, затем при расчете непосредственно фундамента.

Выводы. При любом расчете важно соблюсти последовательность:

2) Выбор расчетной схемы.

3) Определение усилий N, M и Q.

4) Расчет элемента по первому предельному состоянию (по прочности и устойчивости).

5) Расчет элемента по второму предельному состоянию (по деформативности и трещиностойкости).

Источник