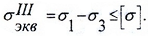Прочность по касательным напряжениям что это

Проверка прочности балок при изгибе по касательным и главным напряжениям.

Проверка по касательным выполняется для опасного сечения балки, где поперечная сила по модулю принимает наибольшую величину. Условие прочности при этом имеет вид:

, используя это условие прочности решается два типа задач:

1) Проверочная задача

2) Проектировочная задача НЕ РЕШАЕТСЯ, т.к. размеры сечения определены из условия прочности по нормальным напряжениям.

3) Определение несущей способности балки Qmax ….

Для сплошных сечений типа прямоугольник и ему подобные, величина много меньше, чем и поэтому такие сечения по главным напр. НЕ прверяются. Для сечений типа двутавр, проверка ОБЯЗАТЕЛЬНА и производится для точки 2С, в которой и норм. и касат. напряжения большие по величине.

Проверку по главным напряжениям выполняем, используя след. условие прочности:

Касательные напряжения при поперечном изгибе.

В 1855г. Д.И. Журавский получил следующую зависимость для определения касательных напряжений при поперечном изгибе балок.

Q- поперечная сила (берём с эпюры Q с соответствующим знаком).

S — статический момент отсечённой части сечения на уровне определяемых касательных напряжений.

I -момент инерции всего поперечного сечения балки.

-параболический закон изменения 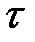по высоте балки.

Рассмотрим использование формулы Журавского на примере прямоугольного сечения с размерами b и h. Требуется определить величину касательных напряжений на удалении оси y от оси x.

34.Определение критической силы при потере устойчивости сжатого стержня(вывод формулы Эйлера).Пусть стержень длиной L шарнирно опертый сжат продольными силами F.При некотором значении F=Fкр плоскости наим. Жесткости EJmin происходит выпучивание стержня т.е. он теряет продольную устойчивость.

Запишем диф.уравнение изогнутой оси стержня для произвольной оси Z.

EJmin = (z)=-Fкр.J

+ y=0 (2)

+ y=0

=

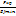
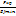
Однородн. диф. Уравнение 2 порядка.Решение уравнения (2) ищем в виде:

1) z=0, y=0, C2=0

2) z=L, y=0; 0=C1*sinkz

C1≠0 т.к. стержень изогнутый

3)K= n

Fкр= (3)

Fкр= (4) – формула Эйлера получена в 1744г

Влияние характера закрепления сжатого стержня на его устойчивость.

Формой потери потери устойчивости сжатого стержня при выводе формулы Эйлера является полуволна синусоиды:

Y=fsin (5)

В тех расчетных случаях когда условия опирания стержня от выше рассмотренного случая по предложению русск. Ученого Ф.С.Ясинского было введено понятие приведенной длины стержня т.е. условной длины приведенной к полуволне синусоиды:

=µ (6)

Ln- приведенная длина

Е- фактическая

µ- коэф. Приведения

последняя конструкция устойчивее по сравнению с 1 в 16 раз и тогда окончательно форм. Эйлера принимает вид:

Fкр= (7)

ПРЕДЕЛЫ ПРИМЕНИМОСТИ ФОРМУЛЫ ЕЙЛЕРА

Классификация стальных стержней

F= 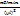формула позволяет определить величину критических напряжений

σ_кр =

-минимальн радиус инерции поперечн сечения стержня,то

σ_кр =

λ -безразличный параметр,называемый гибкостью стержня,в зависимости от λ стержни подразделяют на 3 класса

I-стержни малой гибкости или жесткие стержни

II-стержни средней гибкости

III-стержни высокой гибкости или гибкие стержни

Формула Эйлера получена на основе диф. ур изогнутой оси стержня, базирующегося назакономерности Гука.

Источник

iSopromat.ru

Важнейшим критерием оценки прочности балок при изгибе являются напряжения.

Рассмотрим способы расчета напряжений при плоском поперечном изгибе балки

Расчет напряжений

Возникающий в поперечных сечениях при чистом прямом изгибе изгибающий момент M_x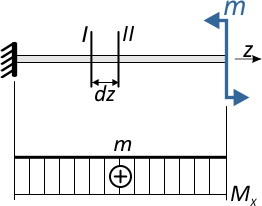

представляет собой равнодействующий момент внутренних нормальных сил, распределенных по сечению и вызывающих нормальные напряжения в точках сечения.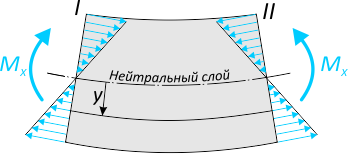

Закон распределения нормальных напряжений по высоте сечения выражается формулой: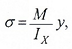

где:
M — изгибающий момент, действующий в рассматриваемом сечении относительно его нейтральной линии X;
I_x — осевой момент инерции поперечного сечения балки относительно нейтральной оси;
y – расстояние от нейтральной оси до точки, в которой определяется напряжение.

Нейтральная ось при изгибе проходит через центр тяжести поперечного сечения.

По вышеуказанной формуле, нормальные напряжения по высоте сечения изменяются по линейному закону.

Наибольшие значения имеют напряжения у верхнего и нижнего краев сечения.

Например, для симметричного относительно нейтральной оси сечения, где y₁=y₂=h/2: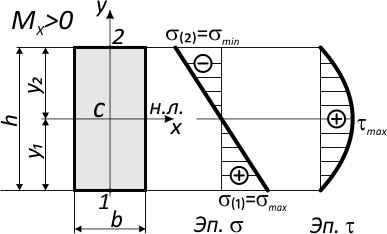

Напряжения в крайних точках по вертикали (точки 1 и 2) равны по величине, но противоположны по знаку.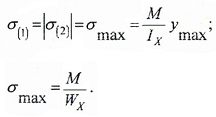

Для несимметричного сечения

напряжения определяются отдельно для нижней точки 1 и верхней точки 2: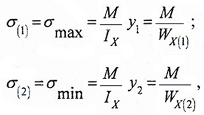

где: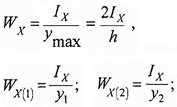

W_X — осевой момент сопротивления симметричного сечения;
W_X(1) и W_X(2) — осевые моменты сопротивления несимметричного сечения для нижних и верхних слоев балки.

Знаки нормальных напряжений при их расчете, рекомендуется определять по физическому смыслу в зависимости от того, растянуты или сжаты рассматриваемые слои балки.

Условия прочности при изгибе

Прочность по нормальным напряжениям

Условие прочности по нормальным напряжениям для балок из пластичного материала записывается в одной крайней точке.

В случае балки из хрупких материалов, которые, как известно, по-разному сопротивляются растяжению и сжатию – в двух крайних точках сечения.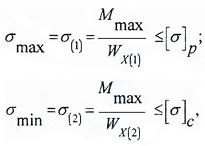

Здесь:
M_max — максимальное значение изгибающего момента, определяемого по эпюре M_x;
[ σ], [ σ]_р, [ σ]_с — допустимые значения напряжений для материала балки (для хрупких материалов – на растяжение (р) и сжатие (с)).

Для балки из хрупкого материала обычно применяют сечения, несимметричные относительно нейтральной оси. При этом сечения располагают таким образом, чтобы наиболее удаленная точка сечения размещалась в зоне сжатия, так как [ σ]_с>[ σ]_р.

В таких случаях, проверку прочности следует обязательно проводить в двух сечениях: с наибольшим положительным изгибающим моментом и с наибольшим по абсолютной величине (модулю) отрицательным значением изгибающего момента.

При расчете элементов конструкций, работающих на изгиб, с использованием вышеуказанных условий прочности решаются три типа задач:

Прочность по касательным напряжениям

В случае прямого поперечного изгиба в сечениях балки, кроме нормальных напряжений σ от изгибающего момента, возникают касательные напряжения τ от поперечной силы Q.

Закон распределения касательных напряжений по высоте сечения выражается формулой Д.И. Журавского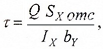

где
S_{x отс} — статический момент относительно нейтральной оси отсеченной части площади поперечного сечения балки, расположенной выше или ниже точки, в которой определяются касательные напряжения;
b_y — ширина поперечного сечения балки на уровне рассматриваемой точки, в которой рассчитывается величина касательных напряжений τ.

Условие прочности по касательным напряжениям записывается для сечения с максимальным значением поперечной силы Q_max:

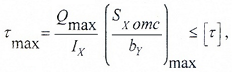
где [ τ] – допустимое значение касательных напряжений для материала балки.

Полная проверка прочности

Полную проверку прочности балки производят в следующей последовательности:

При анализе плоского напряженного состояния главные напряжения при изгибе, примут вид: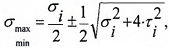

так как нормальные напряжения в поперечном направлении к оси балки принимаются равными нулю.

Проверка прочности осуществляется с помощью соответствующих гипотез прочности, например, гипотезы наибольших касательных напряжений:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Основы сопромата. Определение касательных напряжений.

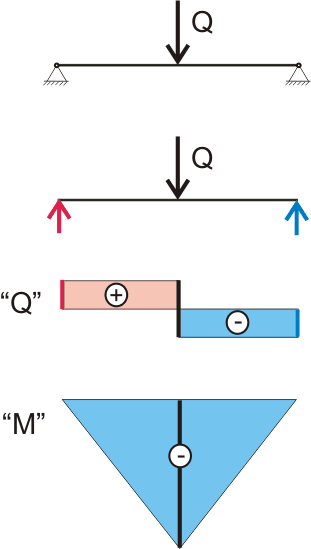
Ранее мы для простоты и наглядности рассматривали обычную деревянную линейку в качестве балки, что позволило с известными допущениями вывести основные уравнения и формулы для расчета несущей способности балки. Благодаря этим уравнениям мы построили эпюры поперечных сил «Q» и эпюры изгибающих моментов «М».

Рисунок 149.2.1. Эпюры поперечных сил и изгибающих моментов, действующих в поперечных сечениях балки при сосредоточенной нагрузке.

Что в итоге позволило достаточно просто и наглядно определить значение максимального изгибающего момента и соответственно значение максимальных нормальных растягивающих и сжимающих напряжений, возникающих в наиболее нагруженном поперечном сечении балки.

Дальше, зная расчетное сопротивление материала балки (значения расчетных сопротивлений проводятся в соответствующих СНиПах), можно достаточно легко определить момент сопротивления поперечного сечения, а затем и другие параметры балки, высоту и ширину, если балка прямоугольного сечения, диаметр, если балка круглого сечения, номер по сортаменту, если балка из металлического горячекатаного профиля.

Такой расчет на прочность является расчетом по первой группе предельных состояний и позволяет определить максимально допустимую нагрузку, которую может выдержать рассчитываемая конструкция. Превышение максимально допустимой нагрузки приведет к разрушению конструкции. Как именно будет разрушаться конструкция, нас в данном случае не интересует, так как данный сайт посвящен не вопросам теоретических и практических исследований предельных состояний материалов, а всего лишь некоторым методам расчетов наиболее распространенных строительных конструкций.

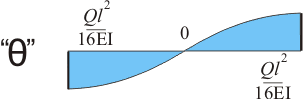
Любая балка, имеющая длину значительно больше, чем высоту поперечного сечения, представляющая собой стержень, под действием нагрузок будет деформироваться. Результатами деформации являются смещение центральной оси балки по оси у относительно оси х, проще говоря прогиб, а также поворот поперечных сечений балки относительно плоскости поперечного сечения. И эти самые прогибы и углы поворота вне зависимости от того, какие опоры у балки и какие на нее действуют нагрузки, также можно определить. Для определения максимального угла поворота и максимального прогиба также строятся соответствующие эпюры, позволяющие определить, какое поперечное сечение сместится в результате прогиба больше всего и какое будет наклонено больше всего.

Рисунок 174.5.6. Эпюра углов поворота при действии сосредоточенной нагрузки посредине балки

Эпюра прогибов здесь не приводится, но как ни странно, это самая простая эпюра, показывающая положение оси, проходящей через поперечные сечения балки в результате деформации и эту эпюру воочию можно наблюдать на любой достаточно прогнувшейся балке или любой другой конструкции. Зная модуль упругости материала балки и момент инерции поперечного сечения определить максимальный прогиб также не очень сложно. Максимально упростить решение этих задач позволяют расчетные схемы для балок, к которым в зависимости от характера опор и вида нагружения даны соответствующие формулы.

Такой расчет деформаций является расчетом по предельным состояниям второй группы и достаточно наглядно показывает, на какую величину прогнется балка. Это бывает важно не только в связи с технологическими ограничениями, например для подкрановых балок, но также и из эстетических соображений. Например, когда потолок, а точнее перекрытие, хотя и достаточно прочное, заметно прогнется, то приятного в этом мало. Максимально допустимые величины прогибов для различных строительных конструкций приводятся в СНиП 2.01.07-85 «Нагрузки и воздействия» (в его актуализированной редакции). Впрочем при расчетах для себя никто не запрещает использовать еще меньшие значения прогиба.

Тут у читателя может возникнуть вполне резонный вопрос, а зачем понадобилось строить эпюру касательных напряжений «Q», если ни в каких расчетах эта эпюра не участвует. Что ж, пришло время ответить на этот вопрос.

Как следует из определения, касательные напряжения действуют в плоскости поперечного сечения, как бы касаются поперечного сечения потому и названы касательными. Определить значение касательных напряжений на первый взгляд просто: достаточно разделить значение поперечной силы (для этого нам и нужна эпюра «Q»), на площадь поперечного сечения (в рассматриваемом нами примере поперечные силы действовали только вдоль оси у и далее этого нам вполне хватит, усложнить любой расчет мы успеем всегда):

т = Q/F = Q/(bh) (270.1)

В итоге мы можем построить эпюру касательных напряжений «τ«(в дополнение к нормальным напряжениям «σ») следующего вида:

Рисунок 270.1. Предварительная эпюра касательных напряжений «τ«

Однако такая эпюра касательных напряжений была бы справедлива для некоего абстрактного материала, обладающего линейной упругостью вдоль оси у, и абсолютно жесткого вдоль оси z, в результате чего в поперечном сечении такого материала не происходит перераспределения напряжений и есть только один вид деформации относительно оси у. В действительности же любое тело, обладающее изотропными свойствами, под действием нагрузок пытается сохранить свой объем, а значит и рассматриваемое нами сечение пытается сохранить свою площадь. Наглядный пример, когда вы садитесь на мяч, высота его под действием вашего веса уменьшается, но увеличивается ширина. Причем процесс этот носит не линейный характер. Если вырезать из теста кубик или параллелепипед, а затем надавить на него, то боковые грани станут выпуклыми, подобный процесс происходит и при лабораторных испытаниях на сжатие образцов металла или других материалов.

Кроме всего прочего это означает еще и то, что касательные напряжения, действующие вдоль оси у, вызывают появление касательных напряжений вдоль оси z и эпюра касательных напряжений вдоль оси z будет более наглядно показывать изменение касательных напряжений по отношению к высоте балки. При этом форма эпюры будет напоминать боковую грань сплюснутого кубика из теста, а площадь эпюры конечно же не изменится. Т.е. значения эпюры касательных напряжений в самом низу и в самом верху поперечного сечения будут равны нулю, а максимальное значение (при прямоугольном сечении) будет посредине высоты сечения и явно больше Q/F. Исходя из условия равенства площадей эпюр максимальное значение эпюры касательных напряжений не может быть более 2Q/F, да и то только в том случае, если эпюра будет представлять собой два треугольника и в этом случае максимальное значение и есть высота треугольников. Однако как мы уже выяснили эпюра по своему виду больше напоминает часть круга или параболу, т.е. значение максимального касательного напряжения будет составлять около 1.5Q/F:

Рисунок 270.2. Более точная эпюра касательных напряжений.

Серой линией показана предварительно принятая нами эпюра касательных напряжений, но теперь касательные напряжения направлены вдоль оси z.

Математически изменение касательных напряжений в зависимости от высоты сечения можно выразить через изменение статического момента отсеченной части сечения с учетом изменения ширины сечения, так как далеко не всегда балки имеют прямоугольную форму сечения. В итоге формула для определения касательных напряжений (вывод формулы здесь не приводится) имеет следующий вид:

Таким образом, согласно формулы (270.2) максимальное значение касательных напряжений для прямоугольного сечения составит:

т = 12Qbh 2 /(8b 2 h 3 ) = 1.5Q/F (270.3)

Такой же результат дала нам и геометрия.

Впрочем, существует и другой подход к вопросу определения касательных напряжений: под действием нагрузок балка деформируется, при этом максимальные нормальные сжимающие и растягивающие напряжения возникают в самом низу и в самом верху поперечного сечения балки, что можно видеть по эпюре «σ» на рис.270.1.

При этом между волокнами такого неоднородного материала, как древесина, как впрочем и между слоями любого другого материала возникают касательные напряжения, направленные теперь по оси х, т.е. по той же оси, что и нормальные сжимающие и касательные напряжения, возникающие в результате действия изгибающего момента.

Происходит это от того, что каждый рассматриваемый слой испытывает разные по значению нормальные нагрузки и в результате все того же перераспределения напряжений и возникают касательные напряжения. Эти касательные напряжения как бы пытаются расколоть балку на отдельные слои, каждый из которых будет работать как отдельная балка.

Правда, значения R_с90 и R_cк для древесины имеют одинаковое значение, но тем не менее касательные напряжения от действия поперечных сил и от деформаций в результате прогиба принято различать (так как рассматриваются две перрпендикулярные друг другу главные площадки напряжений), да и направление действия касательных напряжений важно при определении общего напряжения в исследуемой точке тела.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

Источник