Призма это что за фигура

Призма. Виды призмы

Если вы уже знакомы с призмой, и хотите для себя просто что-то уточнить, то вам вполне может хватить таблицы, что дана в конце статьи.

Мы же поведем подробный разговор.

Призмой (n-угольной призмой) называется многогранник, составленный из двух равных многоугольников и , лежащих в параллельных плоскостях, и параллелограммов .

Боковые грани – все грани, кроме оснований ( являются параллелограммами ).

Боковые ребра – общие стороны боковых граней ( параллельны между собой и равны ).

Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.

Высота призмы – перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания.

Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания.

Диагональное сечение –пересечение призмы и диагональной плоскости.

Перпендикулярное сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.

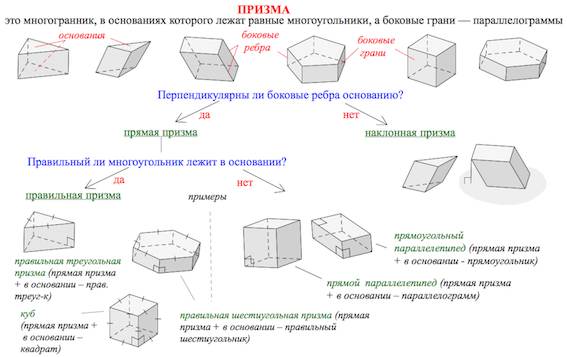
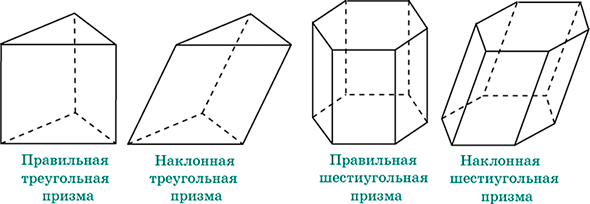
Различают призмы прямые (боковые ребра перпендикулярны плоскости основания) и наклонные (не прямые).

Среди прямых призм выделяют правильные.

Правильная призма – это прямая призма, основанием которой является правильный многоугольник (равносторонний треугольник, квадрат, правильный шестиугольник и т.п.).

Параллелепипед – это призма, основаниями которой являются параллелограммы.

Среди параллелепипедов выделяют наклонные, прямые и прямоугольные параллелепипеды.

Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани — прямоугольники.

Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники (или прямой параллелепипед с прямоугольником в основании).

Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.

Частный случай прямоугольного параллелепипеда – куб.

Куб – прямоугольный параллелепипед, все грани которого – квадраты.

Далее – обещанная таблица, в которой собраны все основные виды призмы, с которыми приходится встречаться на ЕГЭ по математике.

Смотрите также «Объем призмы. Площадь поверхности призмы».

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Источник

Что такое призма: определение, элементы, виды, варианты сечения

В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения призмы. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Определение призмы

Призма – это геометрическая фигура в пространстве; многогранник с двумя параллельными и равными гранями (многоугольниками), а другие грани при этом являются параллелограммами.

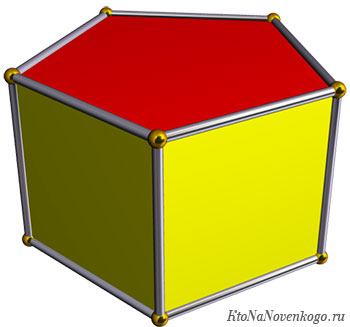
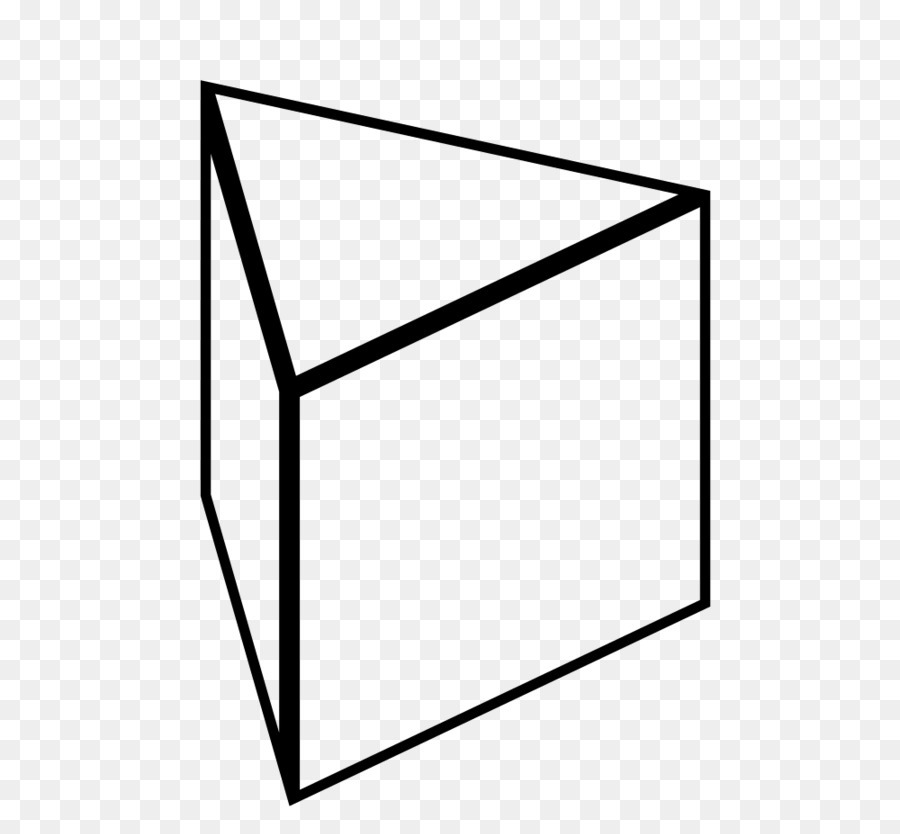
На рисунке ниже представлен один из самых распространенных видов призмы – четырехугольная прямая (или параллелепипед). Другие разновидности фигуры рассмотрены в последнем разделе данной публикации.

Элементы призмы

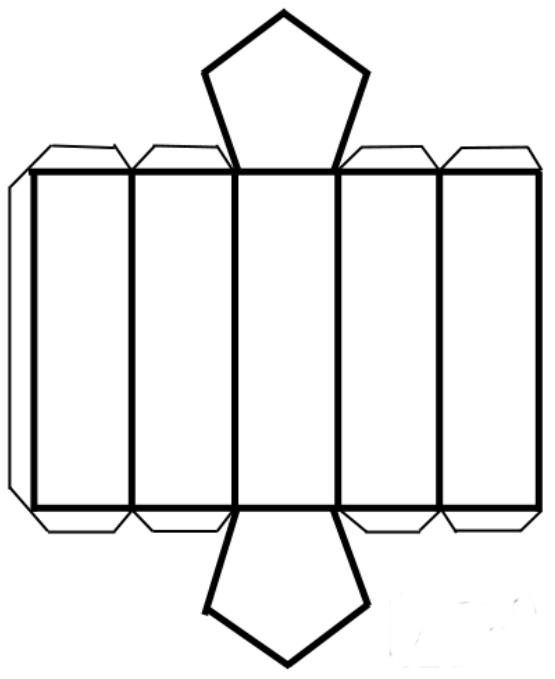
Развёртка призмы – разложение всех граней фигуры в одной плоскости (чаще всего, одного из оснований). В качестве примера – для прямоугольной прямой призмы:

Примечание: свойства призмы представлены в отдельной публикации.

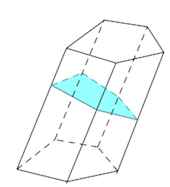
Варианты сечения призмы

Примечание: другие варианты сечения не так распространены, поэтому отдельно на них останавливаться не будем.

Виды призм

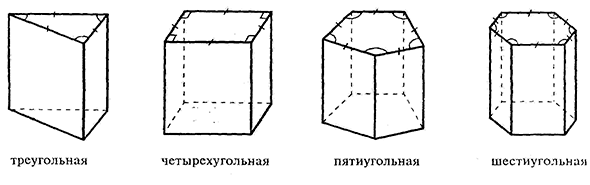
Рассмотрим разновидности фигуры с треугольным основанием.

Источник

Что такое призма — определение и разновидности призм

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы расскажем о такой интересной геометрической фигуре, как ПРИЗМА.

Школьники сталкиваются с ней на уроках геометрии только в 10 классе. Соответственно, те, кто решил уйти после 9-го класса в колледж, этих знаний лишены. И мы восполним этот пробел.

А старшеклассникам наша статья (очень на это надеемся) поможет при подготовке к сдаче ЕГЭ. На экзаменах по математике попадаются несколько вопросов, связанных с ПРИЗМАМИ.

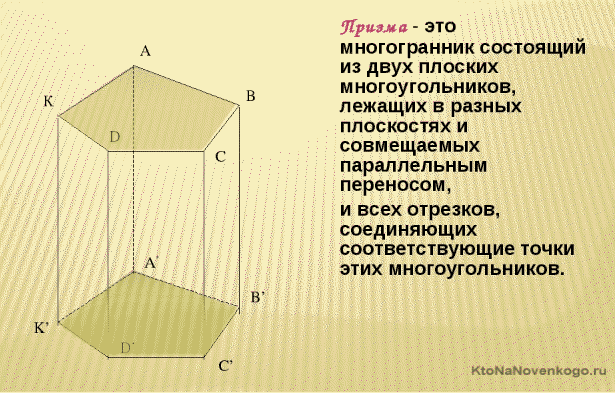
Призма – это геометрическая фигура, которая представляет собой объемный многогранник. Две его стороны лежат на параллельных основаниях и представляют собой различные многоугольники. А боковые грани – это параллелограммы, которые соединяются с основаниями.

Выглядит классическая призма так, как показано на рисунке выше.

На этом рисунке четко видны все элементы призмы:

В зависимости от вида основания призмы бывают:

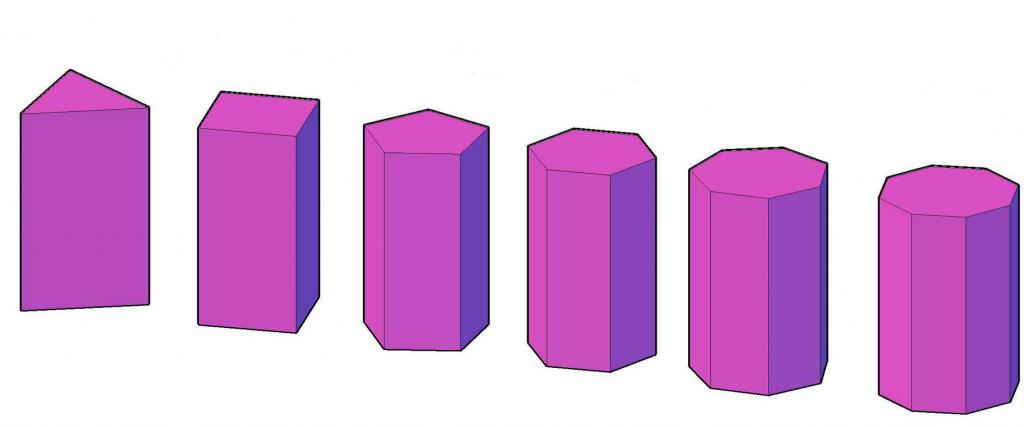
Разнообразие призм можно считать бесконечным. Могут быть фигуры, у которых в основании и 10-угольник, и 20-угольник, и даже 100-угольник. Но, к счастью, такие фигуры попадаются крайне редко. И их точно не изучают в школе.

История изучения призмы

О существовании призм знали еще в Древнем Египте и Древнем Вавилоне. Об этом свидетельствуют различные археологические находки, прежде всего, остатки зданий и памятников.

Но научное описание призм – это заслуга древнегреческих математиков. В первую очередь, Аристотеля. Он даже целое направление науки придумал – стереометрией. В переводе с греческого это означает измерение пространства («метрио» — измерение, «стереос» — пространство).

И в рамках этой науки Аристотель занимался изучением призм, кубов, параллелепипедов и других объемных геометрических фигур.

Естественно, не обошел своим вниманием призмы и знаменитый древнегреческий математик и ученый – Евклид. В своих трудах он дает следующее описание:

Призма – это телесная (то есть пространственная) фигура, которая заключена между несколькими плоскостями. Две из них параллельны друг другу, равны и противоположны. А другие в любом количестве представляют собой параллелограммы.

Элементы призмы

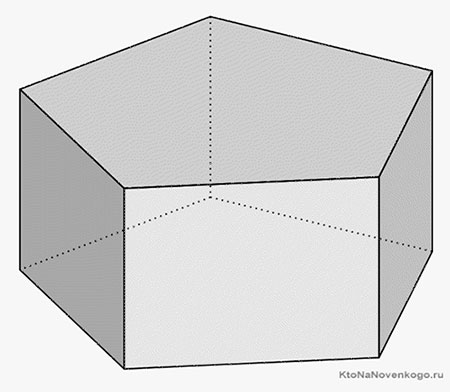
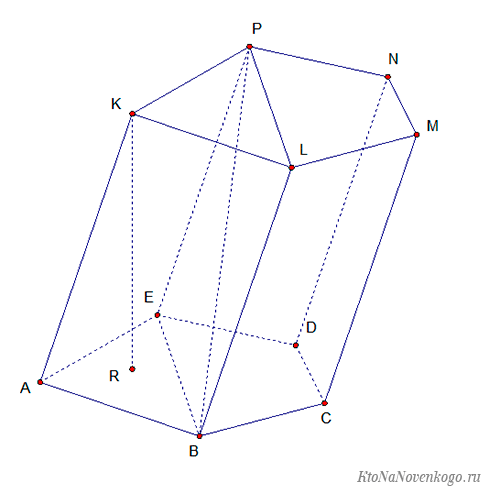
Рассмотрим для примера такую вот призму.

Она пятиугольная и состоит из следующих элементов:

Подобные элементы есть у каждой призмы, независимо от ее вида.

Разновидности призм

Все призмы можно поделить на три категории:

Вместо заключения

Слово ПРИЗМА используется не только в геометрии, хотя именно это значение считается главным. И именно оно первым записано во многих словарях. Но есть и другие варианты:

А еще «Призма» — это кодовое название советской радиостанции 5-АК. Есть такой хоккейный клуб в Латвии – «Призма-Рига». И наконец, в Финляндии существует сеть продуктовых магазинов «PRISMA».

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (2)

Спасибо! Хорошая статья.

Бедные дети, зачем им забивают голову всякими геометрическими призмами? Вообще, если провести опрос среди взрослых, понадобилось ли кому-нибудь это знание, уверен, мы не услышим ни одного положительного ответа.

Источник

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Перечень вопросов, рассматриваемых в теме:

Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.

Боковые грани – все грани, кроме оснований.

Боковые ребра – общие стороны боковых граней.

Основания призмы – равные многоугольники, расположенные в параллельных плоскостях.

Прямая призма – призма, боковые ребра которой перпендикулярны основаниям.

Правильная призма – прямая призма, в основании которой лежит правильный многоугольник.

Площадь полной поверхности призмы – сумма площадей всех ее граней.

Площадь боковой поверхности призмы – сумма площадей ее боковых граней.

Параллелепипед – призма, все грани которой – параллелограммы.

Прямоугольный параллелепипед – параллелепипед в основании которого лежит прямоугольник.

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа,

геометрия. Геометрия. 10–11 классы : учеб. Для общеобразоват. организаций : базовый и углубл. Уровни – М. : Просвещение, 2014. – 255 с.

Открытые электронные ресурсы:

Открытый банк заданий ФИПИ http://ege.fipi.ru/

Теоретический материал для самостоятельного изучения

Определение призмы. Элементы призмы.

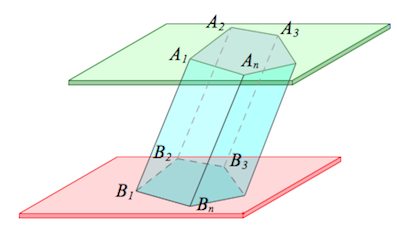
Рассмотрим два равных многоугольника А₁А₂. А_n и В₁В₂. В_n, расположенных в параллельных плоскостях α и β соответственно так, что отрезки А₁В₁, А₂В₂. А_nВ_n, соединяющие соответственные вершины многоугольников, параллельны (рис. 1).

Дадим определение призмы. Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.

При этом равные многоугольники, расположенные в параллельных плоскостях, называются основаниями призмы, а параллелограммы – боковыми гранями призмы. Общие стороны боковых граней будем называть боковыми ребрами призмы.

Отметим, что все боковые ребра призмы равны и параллельны (как противоположные стороны параллелограммов).

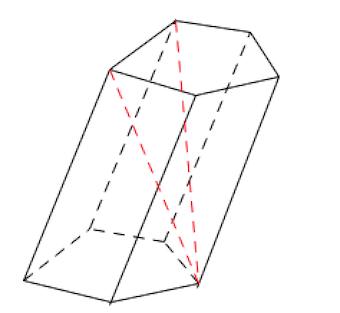
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы. Обратите внимание, что все высоты призмы равны между собой, так как основания расположены на параллельных плоскостях. Также высота призмы может лежать вне призмы (рис. 2).

Рисунок 2 – Наклонная призма

Если боковые ребра призмы перпендикулярны основаниям, то призма называется прямой. В противном случае, призма называется наклонной.

Высота прямой призмы равна ее боковому ребру.

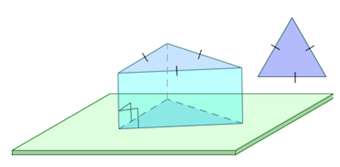
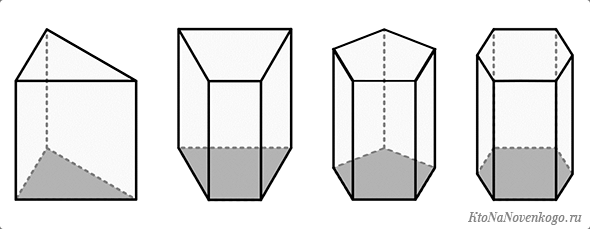
На рисунке 3 приведены примеры прямых призм

Рисунок 3 – Виды призм.

Прямая призма называется правильной, если ее основание – правильный многоугольник. В правильной призме все боковые грани – равные прямоугольники.

Иногда четырехугольную призму, грани которой параллелограммы называют параллелепипедом. Известный вам правильный параллелепипед – это куб.

Площадь полной поверхности призмы. Площадь боковой поверхности призмы.

Площадью полной поверхности призмы (S_полн) называется сумма площадей всех ее граней, а площадью боковой поверхности (S_бок) призмы – сумма площадей ее боковых граней.

Таким образом, верно следующее равенство: S_полн= S_бок+2S_осн, то есть площадь полной поверхности есть сумма площади боковой поверхности и удвоенной площади основания.

Чему равна площадь боковой поверхности прямой призмы?

Теорема. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

Боковые грани прямой призмы – прямоугольники, основания которых – стороны основания призмы, а высоты равны высоте призмы – h. Площадь боковой поверхности призмы равна сумме площадей боковых граней, то есть прямоугольников. Площадь каждого прямоугольника есть произведение высоты h и стороны основания. Просуммируем эти площади и вынесем множитель h за скобки. В скобках получим сумму всех сторон основания, то есть периметр основания P. Таким образом S_бок=P_оснh.

Пространственная теорема Пифагора

Прямой параллелепипед, основание которого – прямоугольник называется прямоугольным.

Теорема. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его ребер, исходящих из одной вершины.

Рисунок 4 – Прямоугольный параллелепипед

Рассмотрим прямоугольный параллелепипед ABCDA₁B₁C₁D₁ и найдем квадрат длины его диагонали А₁С.

Для этого рассмотрим треугольник А₁АС:

Ребро АА₁ перпендикулярно плоскости основания (ABC) (т.к. параллелепипед прямой), значит АА₁ перпендикулярна любой прямой, лежащей в плоскости основания, в том числе АС. Таким образом, ΔА₁АС – прямоугольный.

По теореме Пифагора получаем: А₁С 2 =АА₁ 2 +АС 2 (1).

Так как в основании прямоугольник, то ВС=АD.

Что и требовалось доказать

Доказанная теорема является аналогом теоремы Пифагора (для прямоугольного треугольника), поэтому ее иногда называют пространственной теоремой Пифагора.

Примеры и разбор решения заданий тренировочного модуля

Найдите для каждой картинки пару

1)2) 3)

4)5)

6)

Все изображения можно разделить на две группы: призмы и многоугольники. Вспомним, что основанием призмы является многоугольник. Теперь необходимо посчитать количество вершин многоугольников в основаниях призм и сопоставить их с нужным изображением. Таким образом, получаем следующий ответ: 1 и 3, 2 и 4, 5 и 6.

Какие из перечисленных объектов могут быть элементами призмы?

1) параллельные плоскости

Вспомним сначала, какие элементы есть у призмы. Это ребра, грани, вершины, основания, высота, диагональ.

Ребра, высота и диагональ призмы представляют собой отрезок. Грани и основания – это многоугольники, то есть части плоскостей. Вершины – точки. Таким образом, подходят варианты 2, 3,4.

Источник

Геометрическая фигура призма: определение, виды, формулы площади поверхности и объема

Что такое призма?

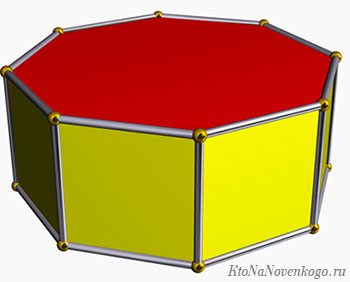
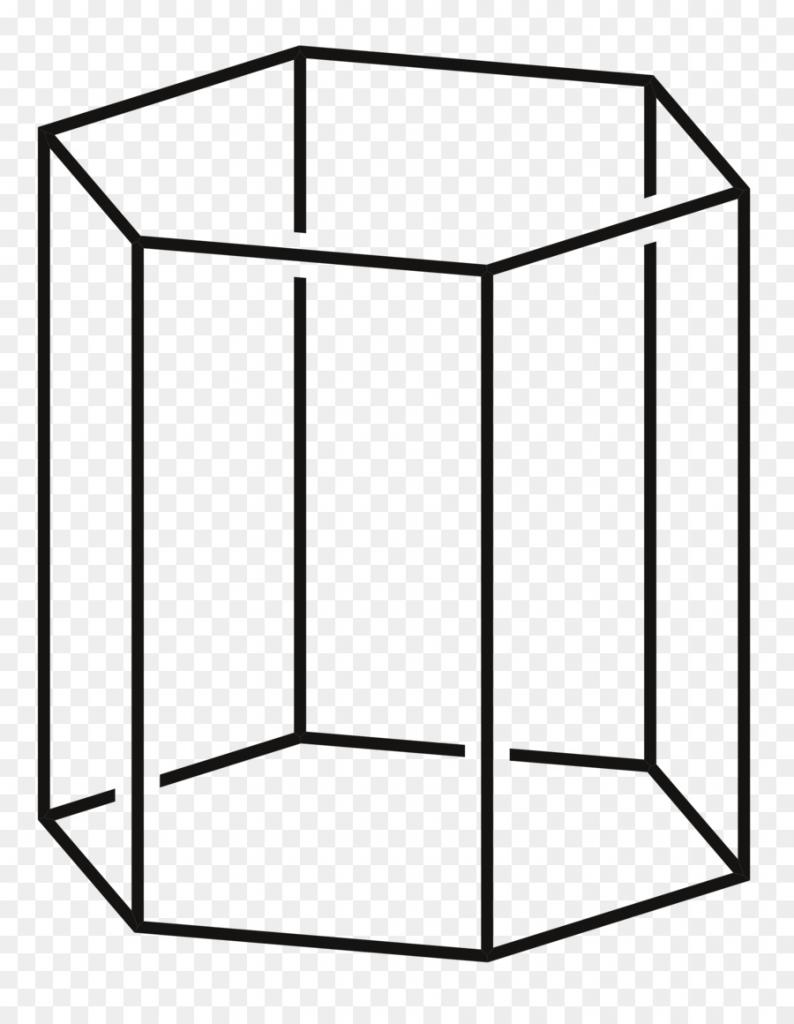
Прежде чем дать определение призмы, представим себе произвольный многоугольник на плоскости. Воспользовавшись операцией параллельного переноса этого многоугольника в пространстве, мы получим объемную фигуру. Эта фигура будет состоять из двух одинаковых многоугольников и нескольких параллелограммов. Это и есть призма произвольной формы. Рисунок ниже показывает, как выглядит шестиугольная призма.

Таким образом, можно дать следующее определение призмы: это объемная фигура, которая образована n параллелограммами и двумя одинаковыми n-угольными сторонами, расположенными в параллельных плоскостях. Одинаковые n-угольники называются основаниями фигуры, а ее параллелограммы образуют боковую поверхность.

Элементы призмы и ее параметры

В соответствии с определением призмы, можно выделить ее грани, вершины и ребра. Количество граней фигуры равно n+2, из которых 2 грани являются многоугольными основаниями. Количество вершин равно 2*n. Все они являются равноправными и образованы пересечением основания и двух боковых параллелограммов. Наконец, число ребер любой призмы составляет 3*n, причем 2*n ребер относятся к основаниям, а n ребер являются боковыми (образованы пересечением параллелограммов).

Линейными параметрами призмы, знание которых позволяет однозначно определить ее геометрические свойства, являются следующие величины:

Помимо линейных параметров призмы, в задачах по геометрии иногда необходимо знать значения ее двугранных углов, чтобы однозначно описать свойства. Двугранные углы бывают двух видов:

Теорема Пифагора для прямоугольного треугольника позволяет связать значения двугранных углов с линейными параметрами фигуры.

Какие бывают фигуры класса призм?

Выше была приведена шестиугольная призма. Рисунок ниже показывает, как выглядит треугольная призма. То есть первой классификацией фигур изучаемого класса является количество сторон основания. Если это количество будет стремиться к бесконечности, то мы получим цилиндрическую поверхность.

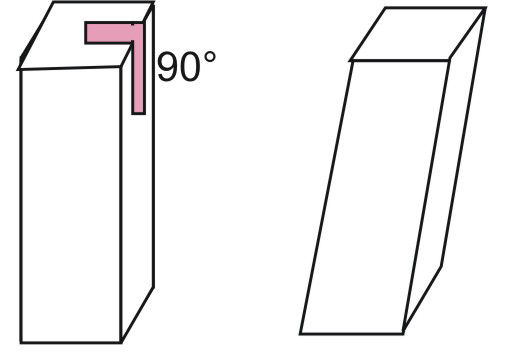
Второй тип классификации зависит от формы боковых сторон. Выше было сказано, что они являются параллелограммами. Однако, если эти параллелограммы одновременно будут прямоугольниками или квадратами, то такая фигура называется прямой призмой. В противном случае говорят о косоугольной или наклонной фигуре. Как выглядит прямая и наклонная четырехугольные призмы, можно увидеть на рисунке ниже.

Заметим, что у прямых призм длины всех боковых ребер b_i равны между собой и равны высоте h.

Третья классификация призм базируется на форме их основания. Оно может быть вогнутым или выпуклым, соответственно призма называется вогнутой и выпуклой.

Правильные призмы удобно изучать в плане таких свойств, как площадь поверхности и объем.

Площадь поверхности

Для рассмотрения вопроса поверхности призмы часто прибегают к изучению ее развертки. Для любой фигуры изучаемого класса развертка состоит из n параллелограммов и 2-х плоских n-угольников. Сложив площади всех граней, мы получим всю поверхность фигуры. Ниже показан пример развертки правильной пятиугольной призмы.

Для правильных призм можно записать общую формулу для площади S их поверхности:

Объем фигуры

Объемом называется величина, которая отражает свойство вещества заполнять пространство. Независимо от вида призмы, ее объем рассчитывается по следующей формуле:

Если призма является правильной, тогда формула для V может быть записана в явном виде:

Как и площадь S, для правильной фигуры объем V также является функцией двух параметров.

Источник